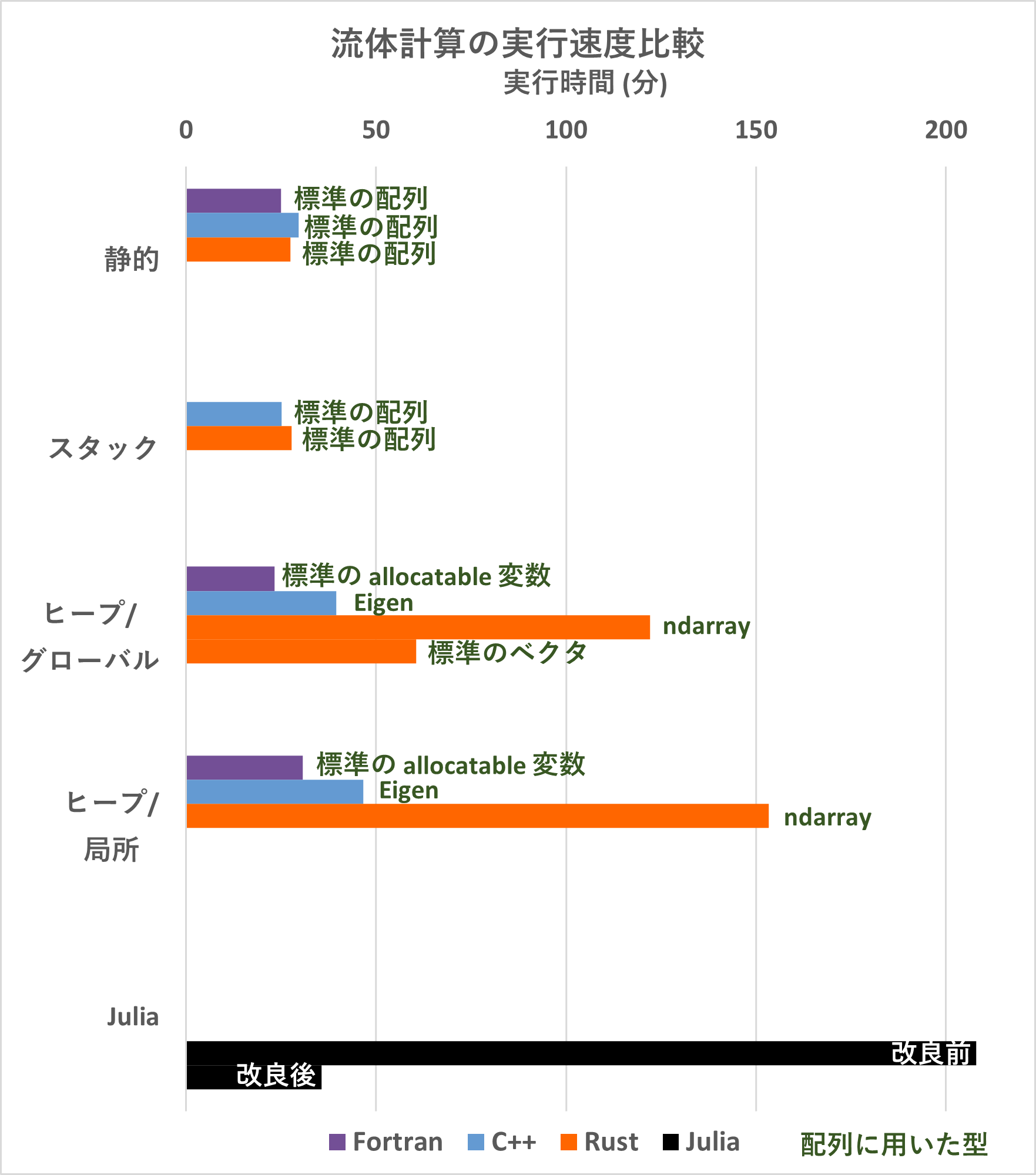
要点
- 下の gif 画像の圧縮性流体計算をするコードを Fortran, C++, Rust, Python, Julia で組み、実行速度を比較した。
- 計算で必要になる巨大配列を、それぞれメモリの静的領域、スタック、ヒープに格納するような 3 バージョンのコードを組んだ。
- ヒープを使わないならば、Fortran, C++, Rust 間の速度差はそこまで無いことが分かった。
- ヒープに配列を割り付けるような外部ライブラリを用いるならば、実行速度はもっと速くならないのか、一考の余地があると思った。
- Julia は書き方によって速度が大きく変化しうる。速い場合は C++ や Fortran 並の速度になるが、その速度にするには習熟が必要と感じた。
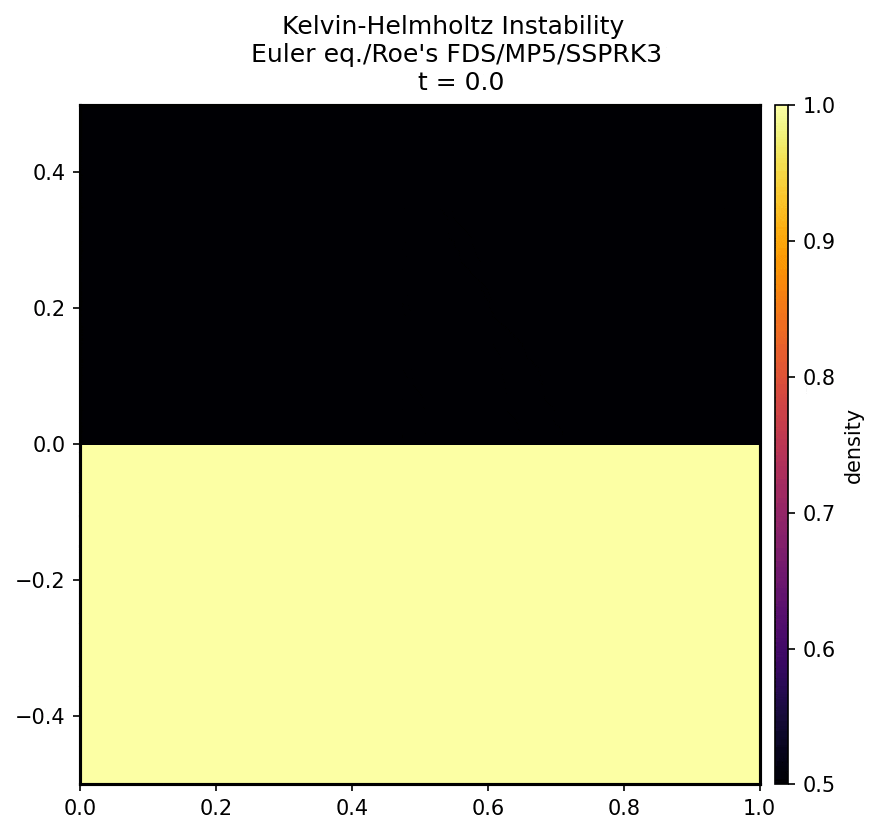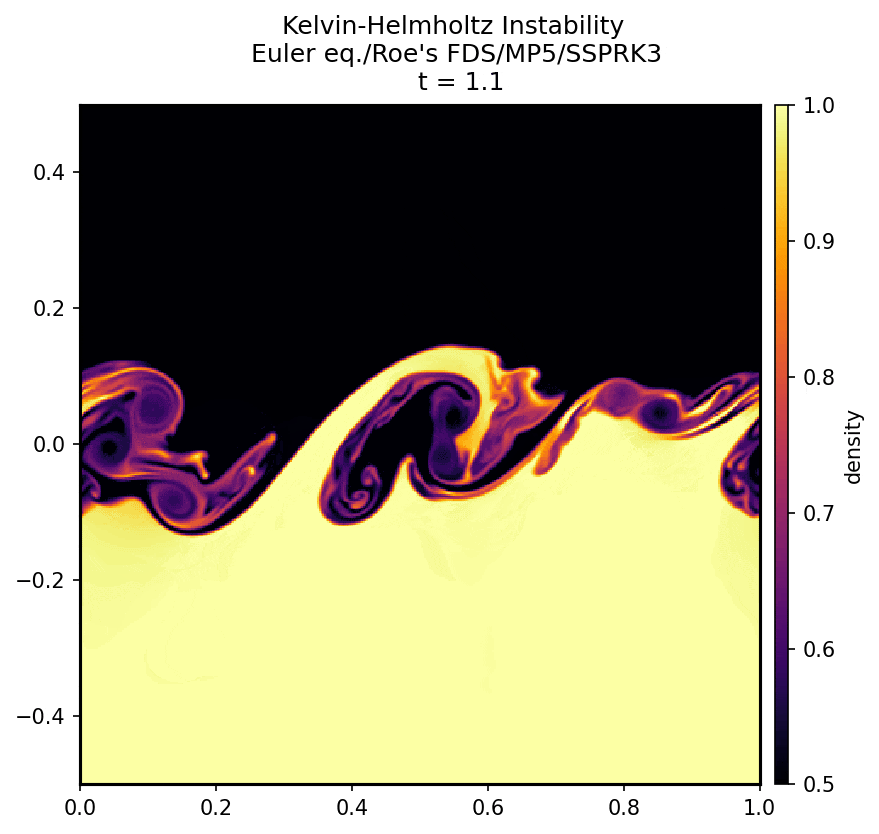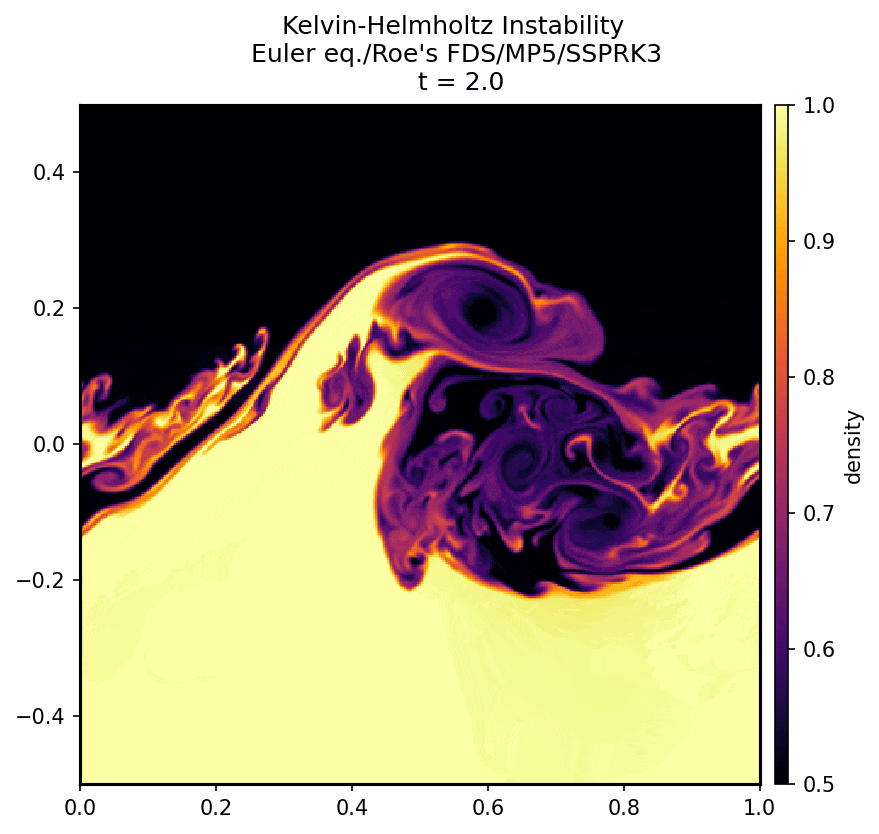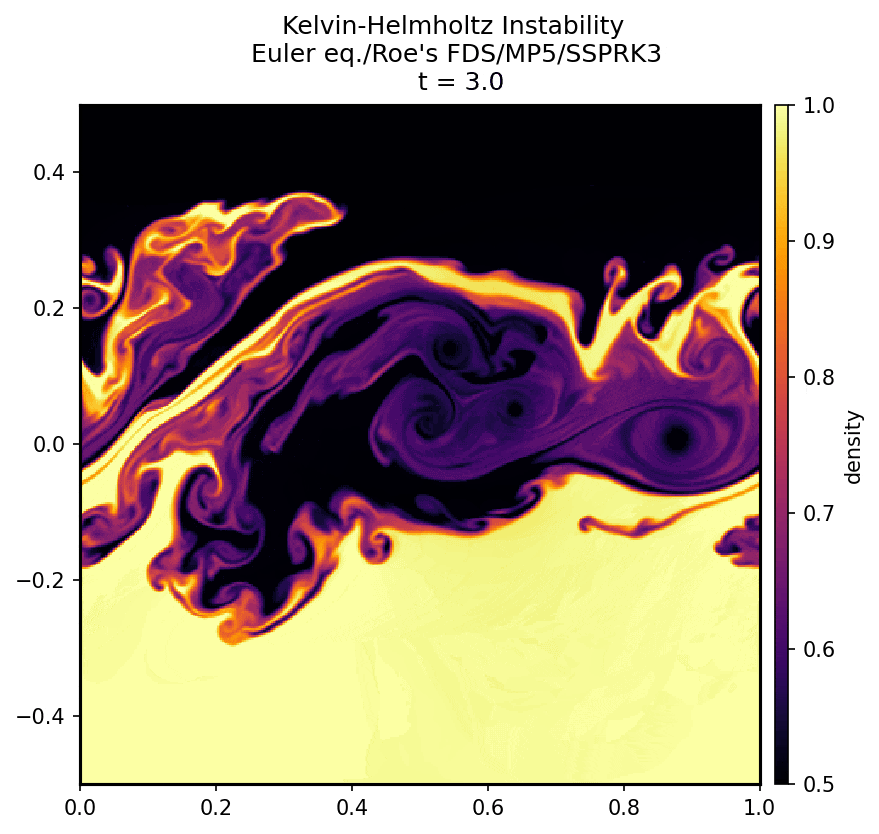
↓ グリッド数 $400\times 400$ の場合の計算結果
\def\sub#1#2{{#1}_{#2}}
オーバーヘッドが発生する余地もそれほどない単純なコードなので、言語比較の観点では面白くないかもしれないが、これから同様のコードを作ろうとしている方の判断材料になればと思い、公開した。
本記事は、再現性のある公平なベンチマークではなく、私が今後どの言語を使って同計算コードを開発していくかの吟味である。よって、それぞれの言語で速度のための最適な書き方をしている訳ではないし、どの言語が一番速いのかを有意に決定したい訳でもない。結果は大雑把な傾向として見るのが適切だと思われる。
計算内容
計算内容を概説する。特に、流体力学的な部分については読み飛ばしていただいても大丈夫だと思う。流体計算に馴染みのない方向けに計算コードの大枠を説明するのがこの節の目的である。
この節の要点
- 2 次元圧縮性オイラー方程式 (マッハ数 0.3) を構造格子上で風上差分法を用いて解き、ケルビン-ヘルムホルツ不安定を再現した。
- $400 \times 400$ 個のグリッドで計算するためには、流体の基本量を格納する $400\times 400$ 配列 4 個の他に、途中で一時的に値を格納するための $400\times 400\times 4$ 配列 5 個分のメモリが必要になる。
- 計算コードの構成としては、配列の各要素に対する四則演算や min, max 比較をループで繰り返す、比較的単純なもの。 if 分岐も 1 箇所小さなものだけ (だったような気がする)。
物理の概要
2 次元の圧縮性オイラー方程式系を解いた。流体は地上の大気を想定し、比熱比 1.4 の理想気体の状態方程式を用いた。方程式は無次元化されているので、パラメータは比熱比以外にはマッハ数だけである。
上の gif 画像のように、$x$ 方向に長さ $1$、$y$ 方向に長さ $1$ の正方形領域で、ケルビン-ヘルムホルツ不安定の再現を行った。$y = 0$ を境に次の 2 種類の初期条件を課し、その後の時間発展を見守る。上側と下側の圧力は等しくした。
- 上側: 密度 0.5、右向きに 1 (マッハ数 0.3) の流速。
- 下側: 密度 1、左向きに 1 (マッハ数 0.3) の流速。
境界条件は次の通り。
- 正方形の上下辺: 初期条件に固定。
- 正方形の左右辺: 周期的境界条件。つまり、右から領域を出ると左から入って来る。
初期状態 $t=0$ から $t=3$ までを計算した。
離散化の方法
等分割の構造格子上で風上差分法を用いた。一般座標変換と境界条件の実装の話を省いて簡単に説明すると、次の通り。
全体の方針
正方形領域を $400\times 400$ のグリッドに等分割し、各グリッドにラベル $(i, j)$ ($i, j = 1,2,...,400$) を付ける。各グリッド上で流体の密度 $\sub{\rho}{ij}$、流速の $x$ 成分 $\sub{u}{ij}$、$y$ 成分 $\sub{v}{ij}$、単位体積あたりの全エネルギー1 $\sub{e}{ij}$ を定義する。つまり、流体の基本量は、$400\times 400$ の配列 4 個で表現される。以下 $N := 400$とする。
初期条件としてこれらの配列の値を与える。のちに述べる手法によって方程式を評価し、微小時間 $dt$ 後の $\sub{\rho}{ij}, \sub{u}{ij}, \sub{v}{ij}, \sub{e}{ij}$ を計算する。その値から同じ計算によってさらに $dt$ 後の配列を求める。これを繰り返す。適切なタイミングで配列をファイルに出力し、それらを連続してカラーマップにプロットしたのが上の gif 画像である。
方程式の評価方法
2 次元圧縮性オイラー方程式系は、質量保存則、運動量保存則 2 成分、エネルギー保存則の計 4 式の連立方程式であり、保存形式で次のように表される (例えば文献 [1])。
\frac{\partial \boldsymbol{Q}}{\partial t} = \frac{\partial \boldsymbol{E}}{\partial x} + \frac{\partial \boldsymbol{F}}{\partial y}\tag{1}
ここで、$\boldsymbol{Q}$, $\boldsymbol{E}$, $\boldsymbol{F}$ は 4 つの成分を持つベクトルであり、$\rho, u, v, e$ の関数である。いま、ある時間ステップ $n$ での配列 $\rho_{ij}, u_{ij}, v_{ij}, e_{ij}$ が求まっているとする。このとき、次のような手順で、次の時間ステップ $n+1$ (時間 $\delta t$ 後) の各配列が計算される。
ステップ 1
各グリッド $i, j$ について、何らかのスキームを用い、現時間ステップでの基本量 $\rho, u, v, e$ から式 $(1)$ 右辺のフラックス $\boldsymbol{E}, \boldsymbol{F}$ を評価する。フラックスの評価には、注目するグリッドでの配列要素に加え、付近のグリッドでの配列要素が必要になる。
\tilde{\boldsymbol{E}}_{i+1/2, j} = \text{flux_scheme}(\rho_{ij}, \rho_{i-1,j}, \rho_{i+1,j},..., u_{ij},..., v_{ij},..., e_{ij},...); \quad \text{for} \ i = 0,..., N; \ j = 1,..., N
\tilde{\boldsymbol{F}}_{i, j+1/2} = \text{flux_scheme}(\rho_{ij}, \rho_{i,j-1}, \rho_{i,j+1},..., u_{ij},..., v_{ij},..., e_{ij},...); \quad \text{for} \ i = 1,..., N; \ j = 0,..., N
物理的には、例えば $\tilde{\boldsymbol{E}}$ については、グリッド $(i, j)$ と グリッド $(i+1, j)$ の間での値を評価しているので、そのことを表すために、添え字が半整数になっている。
ステップ 2
評価されたフラックスを用いて、式 $(1)$ の右辺 (RHS) を次のように評価する。$\delta x$ は隣接するグリッド間の距離。
\text{RHS}_{ij} = \frac{\tilde{\boldsymbol{E}}_{i+1/2,j}-\tilde{\boldsymbol{E}}_{i-1/2,j}}{\delta x}
+ \frac{\tilde{\boldsymbol{F}}_{i,j+1/2}-\tilde{\boldsymbol{F}}_{i,j-1/2}}{\delta x}; \quad \text{for} \ i, j = 1,..., N
ステップ 3
何らかの時間積分スキームを用いて、右辺から次時間ステップでの $\sub{\boldsymbol{Q}}{ij}$ ないしは基本量配列 $\sub{\rho}{ij}, \sub{u}{ij}, \sub{v}{ij}, \sub{e}{ij}$ を計算する。
今回は、ステップ 1 でフラックスを評価するためのスキームに Roe 型 FDS 法 [2] を用いた。これは風上差分法の一種であり、広く用いられる手法である。計算オーダーは各 $(i,j)$ について $O(1)$である。また、風上差分法においては、ステップ 1 において、グリッド間での物理量を評価する際の補完方法の差し替えによって、空間高次精度化が図られる。今回は、5 次精度である MP5 法 [3] を用いて基本変数を補完した。
ステップ 3 の時間積分スキームには、3 次精度の SSP ルンゲ-クッタ法 [4] を用いた。この手法では、次時間ステップでの配列を求めるまでに、式 $(1)$ の右辺を全ての $(i,j)$ に対して 3 回計算する必要がある。しかし、計算オーダーとしては、全ての $(i,j)$ に対して $O(N^2)$ である。
CFL 条件
1 回の時間積分スキームの呼び出しで前進する時間 $\delta t$ は、次の CFL 条件に従わなければならない。
\delta t < \frac{\delta x}{\text{max}(c_s + \sqrt{u^2+v^2})}
$c_s$ は音速である。右辺の分母は、各グリッドでの (音速 + 流速の絶対値) を計算し、それらの最大値を返す意味である。この不等式を満たさないような大きな $\delta t$ を設定して時間積分した場合、計算結果は数値振動を起こし、すぐに爆発 (NaN) してしまう。つまり、グリッド間隔 $\delta x$を小さくすると、それに比例して $\delta t$ も小さくしなければならないので、同じ時間だけ積分するための反復数が増える。
グリッドの総数は $O(N^2)$ で増えるので、同じ時間分を積分するのにかかるプログラム実行時間は、オーバーヘッドの無い理想としては $O(N^3)$ で増える。
今回組んだコードでは、時間ステップを 1 個進めるたびに、新たな基本量から CFL 条件を満たす新たな $\delta t$ を計算し直し、次の時間積分を行う。その際に、上式の右辺を $\nu$ として、$\delta t= 0.7\nu$ と設定した。$t=0$ から $t=3$ まで積分するのに、11370 回程度の反復を要した。
計算コードの構造
上述した計算手順は次のようなアルゴリズムで実装される。Rust 風にして示す。コード構造の見やすさを第一にした不完全なコードなので注意。
// 1 方向のグリッド分割数
const N = 400;
// ステップ 1 と ステップ 2 を実行する関数
// ある時間ステップの基本量 (N*N 配列) を渡すと、方程式右辺 (N*N*4 配列) を返す。
fn calc_rhs(rho, u, v, e) -> [[[f64; 4]; N]; N] {
// ステップ 1: フラックス E の評価
for i in 0..(N+1) {
for j in 0..N {
for k in 0..4 { // k はベクトル E の成分のラベル
E[i][j][k] = flux_scheme("基本量の(i,j) 近辺の配列要素");
}
}
}
// ステップ 1: フラックス F の評価
for i in 0..N {
for j in 0..(N+1) {
for k in 0..4 { // k はベクトル F の成分のラベル
F[i][j][k] = flux_scheme("基本量の(i,j) 近辺の配列要素");
}
}
}
// ステップ 2: 右辺の評価
for i in 0..N {
for j in 0..N {
for k in 0..4 {
RHS[i][j][k] = (E[i+1][j][k] - E[i][j][k]) / dx
+ (F[i][j+1][k] - F[i][j][k]) / dx;
}
}
}
return RHS;
} // fn calc_rhs
// メインプログラム
fn main() {
// 時間
let mut t = 0.0;
// 初期条件を与える
let mut rho = [["密度"; N]; N];
let mut u = [["x 流速"; N]; N];
let mut v = [["y 流速"; N]; N];
let mut e = [["エネルギー"; N]; N];
// 時間積分を繰り返すループ
while t < TMAX {
// CFL 条件から dt を計算
dt = cfl_condition(rho, u, v, e);
// ステップ 3: 時間を dt だけ前進
// 関数 time_marching_scheme() は関数 calc_rhs を 3 回呼び出す。
(rho, u, v, e) = time_marching_scheme(dt, rho, u, v, e);
t += dt;
}
} // fn main
実際のプログラムでは、配列について、なるべく関数内の一時インスタンスを生成しないように、関数の引数を通じて参照で渡して返すような設計にする。しかし、関数 flux_scheme() 内で計算した数値フラックス $\tilde{\boldsymbol{E}}, \tilde{\boldsymbol{F}}$ を一時的に格納するために、$(N+1)\times N\times 4$ 配列が 2 個必要である。また、関数 time_marching_scheme() 内で計算される右辺の値などを一時的に格納するために、$N\times N\times 4$ 配列が 3 個必要になる。
各言語での実装方法
各言語、どのような方針でコーディングしたのかを述べる。
前節で述べたように、流体の状態を表す $N\times N$ 配列 4 個に加え、一時変数として、$N\times N\times 4$ 配列 5 個が必要になる。今回の計算には生かされていないが、用いたコードは等分割ではない歪んだ一般の格子上でも計算できるものである。そのため、グリッド座標とそのメトリクスやヤコビアンを格納するために、$N\times N$ 配列 8 個分のメモリを加えて要求する。合計すると、プログラム実行のためには、少なくとも倍精度実数 $N\times N\times 32$ 個分 = 41 MB のメモリを要する。これらの配列をどのように扱うかがプログラムの実行速度に影響すると思われる。
メモリ領域の性質について
メモリ領域についての自分の知見を示しておく。プログラムが扱うメモリは、次の 3 つの性質の領域に大別されるイメージを持っている (例えば [5])。
- 静的領域: プログラム開始時から終了時までのライフタイムを持つ変数が格納される。ここに格納される配列は、コンパイル時に大きさが分かっていなければならない。アクセスが速い。
- スタック領域: プログラムが実行中に自動で割り付け / 解放をする領域。ここに格納される配列は、コンパイル時に大きさが分かっていなければならない。アクセスが速い。
- ヒープ領域: コードが指定して割り付け / 解放を行わせることのできる領域。コンパイル時に大きさの分からない配列でも、都度格納できる。アクセスが比較的遅い。
環境によって、1 プログラムが扱えるスタック容量の上限が設定されており、それを超えるとスタックオーバーフローを起こし、忌まわしき Segmentation Fault. エラーが返される。
Python 以外の各言語について、上のそれぞれの領域に配列を格納するようなコードを組んで実行速度を比較した。
※追記: ヒープのアクセス速度がプログラムに及ぼす影響と、配列を動的に (ヒープに) 割り付ける際のコストの区別が曖昧である旨のご指摘をコメントで頂いた。そこで、ヒープに割り付けるコードとして、関数を呼び出すたびに一時配列を割り付け / 解放するものと、始めに一度だけ割り付けるものの 2 種類用意して、対比した。
Fortran の場合
メインプログラムの本質部分を抜き出すと、次の通り。
program main
!$ use omp_lib
use parameters ! グローバルパラメータや座標の宣言と設定を行うモジュール
use marching ! 時間積分サブルーチンが定義されているモジュール
implicit none
! 流体の基本変数を宣言
real(8) :: rho(NI, NJ), u(NI, NJ), v(NI, NJ), e(NI, NJ) ! NI = 400, NJ = 400
! 時間変数
real(8) :: t, dt
! 時間ステップ
integer :: tstep
! グリッドの設定と初期条件のインプット
call set_coordinate()
call input_initial(rho, u, v, e)
t = 0.0_8
! ファイル出力のためのループ
do tstep = 1, NOUT ! NOUT は結果をファイル出力する回数
! 時間積分のためのループ
do while( t < real(tstep, 8) * TMAX / real(NOUT, 8) )
! CFL 条件から dt を計算
call calc_cfl(rho, u, v, e, dt)
! dt だけ時間積分
call time_marching(dt, rho, u, v, e)
t = t + dt
end do
! ファイル出力
call output_basic(tstep, rho, u, v, e)
end do
write(*, *) 'Main program ended.'
end program main
Fortran でも構造体を定義できるが、メソッドを関連付けることが出来ないので、コードの見た目を簡素にする程度の役割しかないかもしれない(※)。今回は使わなかった。Fortran はモジュール単位でカプセル化していく言語である。名前空間の概念が無いのが悲しい。
※追記: Fortran でも構造体にサブルーチンを紐づけられることをコメントで教えて頂いた。Type-bound procedures という機能 [6]。
静的変数コード
Fortran では、メインプログラムで宣言された配列は静的領域に格納される。また、モジュール変数やサブルーチン内で宣言した変数も、少なくとも save 属性を付ければ静的領域に格納されるはずである2。よって、グリッド数などのパラメータを宣言したモジュールを作り、他のモジュールから use する。そして、配列を大きさを明示して save 属性付きで宣言した。
スタック変数コード
Fortran の場合、自然にコーディングすると上述した静的変数コードが出来上がるので、コンパイラオプションでスタックに格納するよう指示を出したかったが、gfortran の場合のそれがよく分からなかったので、このバージョンは作っていない。
ヒープ変数コード
allocatable 属性を付けて変数を宣言し、自分で allocate() することで、配列をヒープに格納できる。
その他気を付けたこと、参考情報
- Fortran は配列の格納順序が Column-major なので、配列要素
arr(i, j)をスキャンする場合はiに関するループがjに関するループの内側に来るようにする。逆にするとアクセス速度が結構低下する。 - サブルーチンや関数の引数では、参照渡しが行われるので、新たな配列インスタンス (自動変数) が作られることは無い3 [7]。
- Fortran は標準で多次元配列を定義でき、配列全体の演算も行える。さらに、スライスも使えるので超便利。
C++ の場合
メインプログラムの本質部分を抜き出すと、次の通り。
int main()
{
// 各方向のグリッド分割数
const int NI = 400;
const int NJ = 400;
/* その他いろいろパラメータ設定 */
// 流体を体現するオブジェクトを生成 & 座標の設定 & 初期条件のインプット
static IdealGas2d<NI, NJ> fluid("初期化に必要なパラメータ");
// 時間積分のためのパラメータ
double t = 0.0;
double dt;
double t_out = TMAX / (double)NOUT; // ファイル出力をする時間間隔 = 総積分時間 / ファイル出力数
// ファイル出力のためのループ
for (int tstep = 1; tstep <= NOUT; ++tstep) {
// 時間積分のためのループ
while ( t < (double)tstep * t_out ) {
// CFL 条件から dt を計算
dt = fluid.calc_cfl(0.7);
// dt だけ時間積分
fluid.march_ssprk3(dt, "periodical_in_i", "MP5_basic", "Roe_FDS");
t += dt;
}
// 結果のファイル出力
fluid.output_basic(tstep);
}
std::cout << "Main program ended." << std::endl;
} // main
C++ はインスタンス化可能なクラスを単位にしてカプセル化を行う言語である。C++ の特徴はクラス継承なので、それを生かした設計にした。メインプログラムでインスタンス化しているクラス IdealGas2d は理想気体を体現するクラスであり、メンバ変数として流体の基本量と座標関係の配列、上述した一時変数配列を持つ。各メソッドは適宜それらを参照しながら計算を進める。状態方程式が未定義の継承用クラスから一度継承している。
静的変数コード
fluid オブジェクトを static で宣言すると、そのメンバ変数は静的領域に格納される。そのために、各方向のグリッド数 NI, NJ を const で宣言し、それをテンプレート引数としてクラス IdealGas2d を定義した。テンプレートとは、コンパイル時にコードが都合よく書き換わるように指示を出す機能である。これにより、各メンバ配列の大きさを指定して宣言することが可能になる。
メンバ配列には標準ライブラリの配列を用いた。
スタック変数コード
メンバ配列に標準ライブラリの配列を用い、static を付けずに fluid オブジェクトを宣言することで、メンバ変数がスタックに格納されるようにした。
ヒープ変数コード
メンバ配列に、外部ライブラリ Eigen [8] の ArrayXXd を用いた。これは、ダイナミックに宣言できる配列であり、ヒープに格納される。多次元配列も、Fortran ほどではないが、扱いやすい。また、今回は不要だったが、線形代数計算用のメソッドも揃っている。
その他気を付けたこと、参考情報
- 標準ライブラリの配列やベクタは Row-major なので、要素
arr[i][j]をスキャンする際は、jに関するループをiに関するループの内側に持ってきた方が高パフォーマンス。 - Eigen は、デフォルトでは Column-major なので、逆 (Fortran と同じ)。自分でどちらにするか選べる。
- C++ は、関数の引数を参照渡しにするか、値渡しにするかを自分で選べる。関数宣言/定義時に、引数の宣言を
int aのように行うと値渡し、int& aのように&を付けると参照渡しになる。参照渡しにすれば、新たなインスタンスを作らずに関数外の変数を更新できる。 - 標準ライブラリの配列について、配列の配列を宣言することで多次元配列は扱えるが、配列全体に対して演算を行うには、自分で演算子をオーバーロードする必要がある。スライスは無い。
- Eigen は 2 次元配列までしか扱えないので、3 次元配列
(NI, NJ, 4)は 2 次元配列(NI * 4, NJ)に並び替えることで対応した。
Rust の場合
メインプログラムの本質部分を抜き出すと、次の通り。
fn main() {
// 各方向のグリッド分割数
const NI: usize = 400;
const NJ: usize = 400;
/* その他パラメータ設定 */
unsafe { // static mut な変数を使うには、unsafe {} で囲む必要がある
// 流体を体現するオブジェクトの生成
static mut FLUID: IdealGas::<NI,NJ> = IdealGas::<NI,NJ>::new();
// 座標の設定 & 初期条件のインプット
FLUID.initialize("初期化用パラメータ");
// 時間積分用パラメータ
let dt_out = t_max / n_out as f64; // ファイル出力間隔 = 総積分時間 / ファイル出力数
let cfl_coeff = 0.7;
let mut t = 0.0; // 時間
// ファイル出力のためのループ
for tstep in 1..=n_out {
// 時間積分のためのループ
while t < dt_out * tstep as f64 {
// CFL 条件から dt を計算
let dt = FLUID.calc_cfl(&cfl_coeff);
// 時間積分
FLUID.march_ssprk3(&dt, "periodical_in_i", "MP5_basic", "Roe_FDS")
t += dt;
}
// 結果のファイル出力
FLUID.basic.output(&(tstep as usize));
}
} // unsafe
println!("Main program ended.");
} // fn main
Rust はクラス継承 (というよりクラス自体) が無い。構造体にメソッドや関連関数を紐づけていく言語。カプセル化はモジュール単位で行う。また、可変な参照は同時に 1 度しかできないなどの特有のルールがある 4 (詳しくは [9])。このため、C++ とは異なる全体設計にする必要があった。
メインプログラムでインスタンス化されている構造体 IdealGas はメンバ変数として次のものを持つ。
- 時間積分スキームで必要な一時変数配列 3 個
- 基本変数を体現する構造体: 内部には $\rho, u, v, e$ の 4 配列を持つ。
- 座標を体現する構造体: 内部には座標とメトリクス、ヤコビアン用の配列を持つ。
- オイラー方程式を体現する構造体: 内部にはフラックススキームで必要な一時変数配列 2 個を持つ。
- 状態方程式を体現する構造体: メンバ変数には比熱比を持つ。
- 境界条件を体現する構造体: メンバ変数には境界条件に関連する変数を持つ。
各子構造体はそれぞれ必要なメソッドと関連関数を持ち、他の情報が必要な際は、それを体現する構造体を明示的に渡す。
静的変数コード
FLUID オブジェクトを static mut で宣言すると、内部の変数が静的領域に格納される。Rust は static mut な変数の使用をデフォルトでは認めないので、使うたびに unsafe {} で囲む必要がある。これはコンパイラに「危険であることを認識して使っていますよ」と伝えるためのもの。
static mut で宣言するために、グリッド数を引数に取るジェネリクスを利用して構造体やトレイトを宣言 / 実装した。これは、C++ のテンプレートと似たような機能であり、コンパイル時にコードを都合よく書き換えさせるもの。
各配列には標準の配列を用いた。
スタック変数コード
各配列に標準の配列を用い、static を付けず、普通に let mut でオブジェクトを宣言すれば、構造体内部の変数がスタックに格納される。
ヒープ変数コード
外部クレートの ndarray [10] を用いた。これは、Python の Numpy の使用感を再現しようとしているクレートであり、多次元配列が扱える。Rust の借用ルールのせいで Fortran ほど使い勝手は良くない。ndarray は変数をヒープに割り付ける。
追記:標準のベクタを用いたコードも試してみた。
その他気を付けたこと、参考情報
- 標準の配列も
ndarrayも Row-major なので、配列arr[i][j]をスキャンする際は、jに関するループをiに関するループの内側に持ってきた方が高パフォーマンス。 - Rust は、関数の引数を参照渡しにするか、値渡しにするかを自分で選べる。仮引数の型名の前に
&を付け、実引数の前にも&を付ければ参照渡しになる。さらに、&mutを付ければ、可変な参照渡しになるので、自動変数として新たなインスタンスを作らずに、関数外の変数を更新できる。 - 標準の配列について、配列の配列を宣言することで多次元配列は扱えるが、配列全体に対して演算を行うには、自分で演算子をオーバーロードする必要がある。スライスはあるが、多次元の場合には使いづらい。
- ファイル入出力について、次のパターン 1 のように、
std::fs::Fileでファイルを開くだけで書き込むと、もの凄く 遅い。パターン 2 のように、std::io::BufWriterを用いれば、他の言語と同じ速さになる [11]。
// パターン 1
let mut file = std::fs::File::create("ファイル名").unwrap();
write!(file, "書き込みたい文字列や数値 {}", num).unwrap();
// パターン 2
let mut file = std::io::BufWriter::new(std::fs::File::create("ファイル名").unwrap());
write!(file, "書き込みたい文字列や数値 {}", num).unwrap();
Python の場合
Python の強みは、計算速度を気にしないような解析コードを気軽に書けるところなので、実行速度相撲の土俵に上がらせるのがかわいそうだが、上 3 つの言語の速さを相対化するためにあえて比較してみた。
numpy の配列を用いた。Python はインタプリタ言語なので、for ループは特に遅い。また、メモリ節約を考慮しようと思っても、 numpy とガベージコレクションが中で何をしているのかがよく分からない。そのため、メモリ節約は考えず、配列の切り貼りによって for ループを時間積分に関する 1 回しか使わないような書き方をした。numba のような JIT コンパイラは用いなかった。
(追記) Julia の場合
Julia は、 numba のような JIT コンパイラがデフォルトで動いてくれる Python というイメージの言語である。Python のように気軽に書け、なおかつ for ループも気にすることなく用いることができる。標準で多次元配列やスライスも快適に扱える。今回は用いなかったが、標準で線形代数計算も色々とできる。動的型付けであり、多重ディスパッチという機能を用いて手軽にポリモーフィズムを実現できる。数値計算がしやすいように特化している。
Julia は書き方によって、コンパイラの最適化のかかり具合が結構異なるイメージを持っている。普段は Julia を簡単な解析用途の程度にしか用いないので、実行速度のためのベストな書き方をしていない可能性がある。この記事での結果は、特別詳しいわけではない人間が、Julia の気楽に書ける良さを殺さない範囲で書いた結果として見るのが適切だと思われる。基本的には公式サイトの Tips [12] を眺めて書いた。次のような方針である。
※追記 (2024 年 12 月 4 日):
Julia のソースコードを公開したところ、@SatoshiTerasaki 氏がコードの改良を行ってくださった。それによって、実行速度が大幅に改善した (結果の節参照)。改良の内容は次の通り。特にいちばん上の変更の効果が大きいようだ。具体的なコード差分は Github で見ることができる (ソースコードの節に張ったリンク参照)。
- 一部の固定長かつ値の再代入が行われない配列にパッケージ
StaticArrays.jl[13] のSVectorとSMatrix型を用いる。 -
@viewマクロを用いる。 -
.=を使い忘れていた箇所を修正。
方針
- グローバル変数は用いず、引数で明示的に渡した。
- 構造体の宣言時と、多重ディスパッチのための引数型区別を除いて型宣言はしなかった。
- 関数が型安定になるように気を付けた。また、途中で暗黙的に変数の型を変えないように注意した。
- 配列の演算にはドット演算子を用いた。特に、既存の配列への代入時には、新たなインスタンスが生成されないように、
.=を用いた。 - 配列のスライスには、新たなインスタンスが生成されないように、
viewを用いた。 - 大きな配列を返す関数については、
returnではなく、引数として参照渡しで返した。 - 配列の格納順序が Column-major (Fortran 式) であることに留意して、ループの順序に気を付けた。
- 逐一サブルーチンを作った。最後にメインプログラムを関数
main()で囲み、REPL から実行した。
参考情報
- 型不安定な関数は、コンパイラの最適化がかからないので遅い。型不安定とは、引数の値に返り値の型が依存する状態。例えば、引数を条件に取る if 分岐によって、異なる型の値を返す関数など。
- ドット演算子 (
.+,.-,.*など) は配列の各成分ごとの演算を意味する。基本的にドットを付けた方が速い。 - 既存の配列全体に代入を行う場合、
=を使うと、新たな配列が割り付けられて、そこに左辺の変数を束縛する意味になってしまう。.=を用いると、既存の配列インスタンスの各要素へのコピーの意味になるので、新たに割り付けられることはなく、速い。 - 関数の引数は (本質的には) 可変な参照渡しである。よって、関数内で
.=などを用いて配列の各要素を更新すれば、引数を通じて関数外の配列を更新できる。しかし、関数内で配列全体への代入を=を用いて行ってしまうと、引数とは別の局所変数が宣言されることになるので、見た目上値渡しのような挙動をしてしまう。また、整数や実数のようなプリミティブ型は、=を用いるのがデフォルトなので、実質的に値渡しのようにふるまう。 - 配列のスライスを用いると、新たな配列のコピーが生成されるようなので、それを避ける場合は
view関数または@viewマクロを用いる。
結果
- 使用 CPU: Intel Core i7-11700
- 実行環境 (Fortran/C++/Rust): WSL2 上の Ubuntu 20.04
- Fortran コンパイラ: gfortran 9.4.0
- C++ コンパイラ: g++ 9.4.0
- Rust コンパイラ: cargo 1.65.0
- 実行環境 (Python): Windows 11 / python 3.8.12 / Jupyter Notebook 6.4.6
- 実行環境 (Julia): Windows11 / julia 1.8.3
- 実行環境 (Julia 改良後): Windows11 / julia 1.11.2
いずれのコードも並列化しなかった。gfortran と g++ については、コンパイラオプションに -O3 と -march=native を指定した。cargo については、デフォルト設定の --release モードでコンパイルした。
スタック変数コードについては、スタック上限を小さくするとスタックオーバーフローを起こすことを確認した。逆に他 2 つのバージョンは起こさなかった。ヒープ変数コードについては、使用メモリ量が時間的に揺らいでいることを確認した。逆に、他 2 つのバージョンは揺らがなかった。
コードの時間積分部をコメントアウトし、ひたすら初期条件をファイル出力するだけの状態にしたプログラムの実行時間も測定した。
なお、Python コードについては、$t=0.1$ 程度まで積分したときの計測時間と他 3 つの言語の計測結果を用い、推定した値を示す。
| 言語 | 格納領域 | 割り付け方 | 実行時間 (分) | ファイル出力のみ (分) | 使用メモリ (MB) |
|---|---|---|---|---|---|
| Fortran | 静的 | 24.9 | 0.3 | 45 | |
| ヒープ | グローバル | 23.3 | --- | --- | |
| ヒープ | 局所 | 30.7 | --- | --- | |
| C++ | 静的 | 29.6 | 0.4 | 44 | |
| スタック | 25.1 | --- | --- | ||
| ヒープ (Eigen) | グローバル | 39.5 | --- | --- | |
| ヒープ (Eigen) | 局所 | 46.6 | --- | --- | |
| Rust | 静的 | 27.5 | 0.4 | 43 | |
| スタック | 27.8 | --- | --- | ||
| ヒープ (ndarray) | グローバル | 122 | --- | --- | |
| ヒープ (ndarray) | 局所 | 153 | --- | --- | |
| ヒープ (標準ベクタ) | グローバル | 60.5 | --- | --- | |
| Python | 811* | --- | 200~300 程度 | ||
| Julia | 208 | 0.3 | 300~350 程度 | ||
| Julia (改良後) | 35.6 | --- | 400~450 程度 |
※追記: 「ヒープ/局所」は、関数呼び出しのたびに一時配列の動的割り付け / 解放を行うもの。「ヒープ/グローバル」は、始めに 1 度だけ、ヒープに割り付けるようにしたもの。
※ 例えば、Rust/静的の場合、#[inline] アトリビュートを適切に書き、lto = true を設定してコンパイルすると、実行時間が 18 分程度になったりする。数割の不確かさが付いたものとして見るのが適切だと思われる。
※ Fortran の O2 最適化での実行時間は 32.8 分程度。
※追記 (2024 年 12 月 4 日): Julia の節に詳述したしたように、@SatoshiTerasaki 氏によって改良された Julia コードの実行時間も加えた。既存のコードも併せて実行することで、自分の実行環境に大した変化がなく、表の他の結果と比較できることを確認した。
傾向
- ファイル出力時間は無視できる。
- 静的領域やスタックを用いると速い。
- 何度も動的割り付け / 解放を行うと遅くなる。
- Fortran の
allocatable変数使用によるコストは、動的割り付けの際に発生する分のみと考えて良さそう。 - 外部ライブラリの配列を用いたコードは結構遅い。特に、Rust の
ndarrayは何かしらの無視できない機構が中で働いていそう。 - 静的領域やスタックを用いた場合、Fortran, C++, Rust の間にそこまで大きな差は無い。
感想
- 外部ライブラリを用いていないコードは、そこまでオーバーヘッドが発生する余地のない単純なものだったので、言語間にそこまで差が無いのも納得。
- ヒープを使わなくて良いコードなら、実行速度ではなくプログラム構成との相性、書きやすさによって言語選択をするべき。
- 基本的には静的な配列を用いた方が速そう。ただし、Fortran の allocatable 変数は普通に速い。
- 多次元配列の扱いについては、Julia と Python, Fortran が 圧倒的に 快適。
- C++ と Rust は言語の性質が結構違うので、自然に書くと異なるプログラム設計になりそう。
- C++ と Rust は一般のプログラム向けの言語だと感じる一方で、Fortran は配列の扱いにせよ、デフォルトで参照渡しなところにせよ、科学数値計算がしやすいようにチューニングされた良い言語だと感じる。
- プログラムの規模が大きくなってきたときのモジュール管理は Rust がいちばん楽だと感じる。お節介なほどに書き方のルールが定められているのと、VSCode の Rust 公式拡張機能が優秀だから。
- Julia の高速化は私には難しい。もっと勉強が必要と感じた。
やり残したこと
- Rust / ndarray のケースがなぜ遅かったのかを追求したい。自分が使い方を大きく間違えている可能性がある。
- C++ のヒープの場合について、標準ライブラリのベクタで配列を扱うパターンも比較してみたかったが、気力が続かなかった。
ソースコード
「C++/静的」のコードを GitHub に置いた。
「Fortran/静的」、「Rust/静的」、「Julia」のコードも GitHub に置いた。外部向けに成形する余裕がなかったので、書き散らして読みにくい状態かもしれない。申し訳ない。
Fortran: https://github.com/shigunodo/fluid2d_fort_static
Rust: https://github.com/shigunodo/fluid2d_rust_static
Julia: https://github.com/shigunodo/fluid2d_julia
参考文献
[1] 藤井孝藏. (1994). 『流体力学の数値計算法』. 東京大学出版会.
[2] Roe, P. L. (1981). Approximate Riemann solvers, parameter vectors and difference schemes. Journal of Computational Physics, 43, 357-372. https://doi.org/10.1016/0021-9991(81)90128-5
[3] Suresh, A., & Huynh, H. T. (1997). Accurate monotonicity-preserving schemes with Runge–Kutta time stepping. Journal of Computational Physics, 136, 83–99. https://doi.org/10.1006/jcph.1997.5745
[4] Shu, C.-W., & Osher, S. (1988). Efficient implementation of essentially non-oscillatory shock-apturing schemes. Journal of Computational Physics, 77, 439–471. https://doi.org/10.1016/0021-9991(88)90177-5
[5] Fortran の記憶領域について (Qiita の記事) https://qiita.com/cure_honey/items/29ec979d3548fb4e74c9
[6] Derived Types - Fortran のチュートリアル https://fortran-lang.org/en/learn/quickstart/derived_types/#type-bound-procedures
[7] 6.4.2 Argument passing conventions (gcc のサイト) https://gcc.gnu.org/onlinedocs/gfortran/Argument-passing-conventions.html
[8] Eigen の Wiki https://eigen.tuxfamily.org/index.php?title=Main_Page
[9] 第 5 章 - データの所有権と借用 - Rust ツアー https://tourofrust.com/chapter_5_ja.html
[10] Rust / ndarray の DOCS https://docs.rs/ndarray/latest/ndarray/
[11] Rustで高速な標準出力 - κeenのHappy Hacκing Blog https://keens.github.io/blog/2017/10/05/rustdekousokunahyoujunshutsuryoku/
[12] Performance Tips (Julia 公式サイト) https://docs.julialang.org/en/v1/manual/performance-tips/
[13] StaticArrays.jl https://juliaarrays.github.io/StaticArrays.jl/stable/