描かれた物体周りの流れを計算するウェブアプリを作った忘備録：その１、流体計算編

はじめに

格子ボルツマン法による 2 次元流体計算をブラウザにさせるウェブアプリを作った。ユーザーが自由に描いた物体を一様流中に置き、流れの様子を見守ることができる。流線は LIC 法によって可視化した。アプリの UI とお絵かきの部分は JavaScript、流体計算と可視化の部分は WebAssembly (Rust の wasm-bindgen) によって実装されている。この記事では、実装のために必要だった知見 (を得るために必要な情報) を忘備録としてまとめる。

今回は、アプリの全体構造について述べたあと、流体計算に関する部分と、その実装に用いた WebAssembly の利用方法についてメモする。可視化 (プロット) に関する部分はその２の記事にまとめたので、併せて読んで欲しい。アプリの UI の実装、お絵かきモードの実装についても、別の記事にしてまとめたい。

実装されたアプリは以下のページに置かれている。楽しくて癒されるアプリなので、ぜひ遊んで欲しい。高スペックのパソコンやタブレット推奨。

気に入っていただけたら、ぜひ以下のツイートも拡散して欲しい。

2次元流体計算をブラウザに計算させるウェブアプリを作りました。格子ボルツマン法を用いています。ユーザーが自由に描いた物体を一様流中に置いて、流れの様子を見守ることができます。 いろいろイジって遊んでください。 #draw_in_flowhttps://t.co/5mac8evgHF pic.twitter.com/IXq6slXEnh

— みね@太陽の科学館 (@solarphys_info) February 16, 2023

ソースコードは次のレポジトリに置かれている。

計算の物理設定

アプリのページに詳しく説明されているので、ここでは割愛する。この記事では、主にアプリの実装方法の部分について説明する。

アプリの全体構造

例えばブラウザに Chrome を用いている場合、アプリのページで右クリックし、メニューいちばん下の「検証」をクリックすることで、ソースコードやその構成を見ることができる。

アプリは次の 4 つのソースコードから成る。

• index.html：HTML によって記述され、ページのリンクが踏まれたら、まずこれが読み込まれる。ブラウザに表示されるページの構成と内容文が書かれている。
• style.css：CSS によって記述されており、index.html によって読み込まれる。ページのデザインを決める。
• main.js：JavaScript によって記述されており、index.html によって読み込まれる。アプリの挙動が定義されている。
• ***.wasm：WebAssembly によって記述されており、main.js によって読み込まれる。流体計算と可視化の部分がこのファイルに実装されている。

main.js は web-pack を用いてバインドしたものなので、ファイル容量を減らすために変数名が短縮されている。

計算結果のプロットには HTML の canvas タグを用いた。アプリの起動時に、JS ファイルにおいて wasm のオブジェクトがインスタンス化され、wasm は独自のメモリ領域を展開し、計算の準備をする。計算開始ボタンが押されると、JS によって wasm のサブルーチンが呼び出される。流体計算 & 可視化の結果は、canvas にプロットするための RGB 情報として、wasm 内に宣言された配列に格納される。JS 側ではその配列を参照し、canvas に出力する。これが計算と描画までの大まかな流れである。

格子ボルツマン法の概要

流体計算スキームとして主に用いられる有限差分法や有限体積法では、ナビエ-ストークス方程式系が離散化されて解かれる。一方、格子ボルツマン法 (Lattice Boltzmann Method, LBM) では、セルオートマトン風に離散化されたボルツマン方程式が解かれる。解かれる方程式は、局所平衡分布からのずれについての高次の項を無視した近似として、非圧縮性の連続の式 & ナビエ-ストークス方程式に帰着する。

LBM の教科書ついては、瀬田剛『格子ボルツマン法』(森北出版, 2021) が良書である。分かりやすく LBM の基礎と実用スキームのエッセンスが説明されているので、この本で入門することを薦める。

また、LBM の雰囲気を知りたい方は、次のウェブサイトを薦める。

上 2 つの文献が優秀なので、ここで詳細を説明するモチベは無い。以下では、他の計算手法と対比したときの LBM の特徴を簡単にまとめておく。

• LBM の長所は、比較的計算が速いことと、境界条件の設定が容易なことである。今回は、お絵かきモードの実装のためにこの手法を選んだ。
• LBM は擬似圧縮性解法の一種である。解く方程式は、近似的に非圧縮性のナビエ-ストークス方程式系に帰着するが、解く際に若干の仮想的な圧縮性を認める。$$p = \frac{\rho}{3}$$ という仮想的な (等温気体のような) 状態方程式が課された流体を計算することになる。
• 基本的に等分割の構造格子上での計算になる。物体形状に対応して計算格子の形を変化させることができないのが欠点。
• LBM は陽解法であるが、(仮想的な分子速度に対する) クーラン数が 1 に固定されるので、移流を正確に解けることが長所である。逆に言うと、格子幅を決めれば時間ステップ幅が固定されてしまう。
• 空間 2 次精度の解法を用いた。科学研究に使われるような有限差分法や有限体積法と比べると、精度は落ちる。因みに、LBM では、衝突項の計算方法を工夫することで、安定化と空間高次精度化、乱流への対応が図られてきた。3 次元計算に関しては、空間 4 次精度の LBM も存在し、乱流遷移の再現を行った研究もある (Geier et al., 2017)。

• 衝突項の計算はそれぞれの格子に対する局所的なものなので、並列化しやすいことが特徴である。しかし、今回は (今のところ) 並列化していない。
• LBM は粒子法と同じく、芸術的な CG 制作にもよく用いられているようだ。GPU による並列計算との相性が良いことが理由のひとつかもしれない。

今回用いたスキーム

重要な点をまとめる。アプリのページも併せて見てほしい。

• アプリで図示される領域の外側にも、計算領域は広がる。外側の領域は、アプリで図示される領域に比べて格子幅が 2 倍に設定されている。両領域の接続方法は後述する。

• 衝突項の計算には、セントラルモーメントを用いた。具体的には、De Rosis (2016) の方法である。これにより、高レイノルズ数でも安定に計算を進められる。

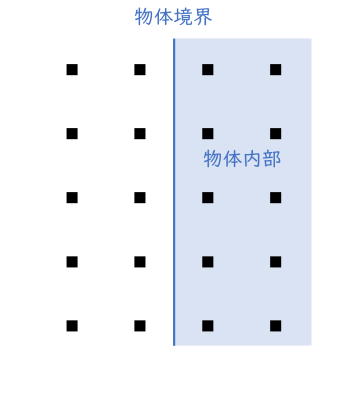
• 物体表面での滑りなし境界条件には、ハーフウェイバウンスバックスキーム (e.g. 瀬田, 2021) を用いた。この方法では、図のように格子点の間に物体境界が設定される。物体境界では、各分子は (スネルの法則ではなく) 速度を反転させるようにして反射されると考える。これを巨視的に見ると、滑りなし条件が課されることになる。

• 計算領域の上辺、下辺、左辺の数値境界では、局所平衡分布を仮定して未知量を補完した。
• 計算領域の右辺の流出境界では、Yang (2013) の "convective condition" を用いた。領域内に与える影響が少ないのが利点だが、安定性は他の境界より悪い。

• 細かい計算格子の領域 (アプリに図示される領域) と粗い計算格子の領域は、空間的に 3 次スプライン補間、時間的に 2 次ラグランジュ補間を用いて滑らかに接続した (マルチブロック法)。詳細は後述する。

マルチブロック法について

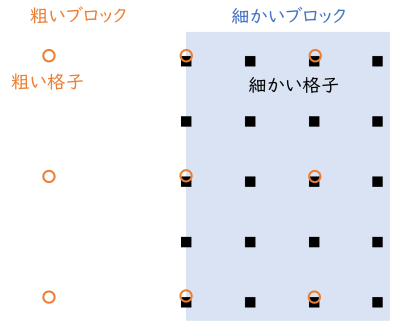
図で表したように、計算領域は 5 個のブロックに分割される。そのうちの、アプリで図示するブロックは、他のブロックより格子が細かい。格子幅にして 1/2、面密度にして 4 倍である。

格子の粗さが等しいブロックは、端から格子幅 1 個分を重ね合わせることで接続される。ブロック A と B が隣接している場合、A の端から一個内側の格子点での計算結果が、次時間ステップでの B の端点の値として利用される。逆も然り。

粗さの違うブロックは図のように重ね合わされる。粗いブロックの端点値は、上と同様にして得られるが、細かいブロックの端点値を粗いブロックの計算結果から得るには、値を補間しなければならない。この補間には 3 次のスプライン補間を用いた。

スプライン補間については、例えば次のウェブサイトが詳しい。瀬田 (2021) でも説明されている。

今回は、格子幅が 1 になるように無次元化して計算しているので、スプライン補間の途中で次の連立方程式を解くことになる。

\underline{A} \vec{x} = \vec{b}\\
\underline{A} := \begin{pmatrix}
4 & 1 & 0 &\cdots&\cdots&\cdots& 0 \\
1 & 4 & 1 & 0 &\cdots&\cdots& 0 \\
0 & 1 & 4 & 1 &\cdots&\cdots& 0 \\
\vdots&   & &\ddots& & &\vdots\\
0&\cdots& 0 & 1 & 4 & 1 & 0 \\
0&\cdots&\cdots& 0 & 1 & 4 & 1 \\
0&\cdots&\cdots&\cdots& 0 & 1 & 4 
\end{pmatrix}

この連立方程式は LU 分解によって解いた。$\underline{A}$ は 3 重の帯行列なので、$\underline{A}=\underline{L}\underline{U}$ と LU 分解すると、$\underline{L}, \underline{U}$ は 2 重の帯行列になる。アプリの起動時にこの帯要素を計算し、保持しておけば、補間時に与えられた $\vec{b}$ に対して前進消去と後退消去を行うことで、$O(n)$ で連立方程式を解くことができる。具体的なアルゴリズムは「LU factorization for a tridiagonal matrix」などで調べれば出てくる。

上述したように、LBM ではクーラン数が 1 に固定されるので、粗いブロックを 1 回時間積分する間に、細かいブロックは 2 回時間積分しなければならない。粗いブロックの計算結果が存在しない時間ステップでの端点値は、時間的に 2 次のラグランジュ補間を行うことで計算した。このため、粗いブロックの 1 ステップ前における接続点での計算結果 (補間結果) を保持しておかなければならない。

WebAssembly について

アプリの流体計算と可視化の部分は WebAssembly (wasm) によって実装されている。wasm はブラウザで動かすことのできる言語 (?) であり、特に複雑な計算をさせる場合は JavaScript より速いことが多い。現在の主要ブラウザではサポートされている。詳細は次のサイト。

今回は、wasm の作成に Rust と wasm-pack, wasm-bindgen を用いた。具体的には、wasm-bindgen クレートの仕様に従って体裁を整えた Rust クレートを作り、wasm-pack を用いて .wasm ファイルを生成する。一緒に生成された .js ファイルを、JavaScript のメインプログラムでモジュールとして import する。それによって、Rust で定義したメソッドを、まるで JavaScript のメソッドのようにして用いることができる。呼び出される実体は .wasm のサブルーチンである。

Rust による wasm の生成方法は、次のサイトのチュートリアルをやることで、一通り習得できる。

wasm は Rust 以外の各言語によっても生成できる。例えば、C++ を用いるならば、Emscripten を用いることになると思う。

wasm-bindgen の使い方

wasm-bindgen クレートを用いることで、wasm にコンパイルするための Rust コードを簡単に書くことができる。上にリンクを載せたチュートリアルを行うことで、wasm-bindgen の使い方は理解できると思う。以下ではその概要と、私がつまづいた点をまとめる。

• 基本的な文法は次の通り。JS 側で使用する構造体やメソッドには #[wasm_bindgen] を付ける。使用しないものには付けなくて良いが、#[wasm_bindgen] を付けた構造体が持つ子構造体には #[wasm_bindgen] とコピートレイトが付与されていなければならない。#[wasm_bindgen] を付与したコンストラクタ関数 fn new() -> Self を作り、JS 側でそれを用いることで、構造体をインスタンス化することになる。

lib.rs

use wasm_bindgen::prelude::*;

const N: usize = 100;

#[wasm_bindgen]
#[derive(Clone, Copy)]
pub struct ChildStruct {
    field: [u8; N],
}

#[wasm_bindgen]
pub struct StructExposedToJS {
    field: f64,
    child: ChildStruct,
    arr: [u8; N], 
}

#[wasm_bindgen]
impl StructExposedToJS {
    pub fn method_exposed_to_js(&mut self, some_arg: f64) {
        self.field = some_arg;
    }
}

　

• 現在のところ、#[wasm_bindgen] とジェネリクスを併用することができない。
• 例えば上の例で、JS 側では StructExposedToJS をインスタンス化する場合を考える。子構造体 ChildStruct に自身を変更するメソッド fn method(&mut self) を紐づけて、#[wasm_bindgen] を付与する。このとき、JS 側でinstance.child.method() によって呼び出しても、上手く動作しないようだ (要検証)。このようなことがあるので、基本的に、JS で使用するメソッドはインスタンス化する親構造体に紐づけるのが良いと思われる。
• 標準のベクタ vec を子構造体に持たせると、コピートレイトを持たないとしてコンパイラに怒られる。ベクタは親構造体に直に持たせる必要があるようだ。
• JS 側から参照したい配列は 1 次元配列として宣言した。後述する理由により、この配列はインスタンス化する親構造体に直に持たせることになった。

今回のアプリでの wasm の役割は、流体の情報 (分布関数をはじめとした変数) を保持し、JS からの命令があればそれを時間積分し、結果を可視化して、その結果を canvas タグに描かせるための RGB 情報として格納することである。RGB 情報が格納された配列は JS からポインターとして参照されることになる。

wasm-pack によるコンパイル

wasm-bindgen クレートを用いて作成した Rust クレート (main.rs じゃなくて lib.rs を持つやつ) を、wasm-pack によって wasm にコンパイルする。

いつも cargo を使う階層 (src/ の上の階層) で次のコマンドを打ち込むと、pkg/ ディレクトリ下に .wasm ファイルと、それを JS 側から利用するときに使う .js モジュールが生成される。

wasm-pack build --release --target web

普通にビルドすると、wasm 実行時にスタックオーバーフローが発生してしまうはずである。wasm が扱えるスタック容量を増やすために、wasm-pack を使う階層に .cargo/ ディレクトリを作り、次のファイルを置いてからビルドする。ここでは 40 MB を指定している。

config

[target.wasm32-unknown-unknown]
rustflags = [
  "-C", "link-args=-z stack-size=40000000",
]

JavaScript 側の書き方

上で生成された .js モジュールをメインプログラムでモジュールとしてインポートする。デフォルト出力されている init() 関数を呼び出すことで、wasm を初期化する。この関数は async func なので、同期的に初期化するために、今回はトップレベル await 式を用いた。

main.js

import init, {StructExposedToJS} from ".js モジュールのパス";
const wasm = await init();

構造体 StructExposedToJS とそのコンストラクタ関数 fn new() -> Self に #[wasm_bindgen] を付与していれば、次のようにして、JS 側で StructExposedToJS をインスタンス化できる。内部処理的には、StructExposedToJS を返す関数が呼ばれた際に、wasm のメモリ領域に StructExposedToJS がアロケートされる。JS 側ではそのメモリを指すポインターが返され、変数名 instance に紐づけられている。

main.js

const instance = StructExposedToJS.new();

StructExposedToJS に紐づけられて、#[wasm_bindgen] を付与されたメソッドは instance.method() のようにして呼び出せる。

wasm が持つ 1 次元配列を JS 側から参照するには、次のようにする。上で定義した StructExposedToJS が持つフィールド arr: [u8; N] を参照したい場合、まずは Rust で次のメソッドを定義する。メソッド get_ptr() は、arr へのポインターを返す。

lib.rs

#[wasm_bindgen]
impl StructExposedToJS {
    pub fn get_n(&self) -> usize {N}
    pub fn get_ptr(&self) -> *const u8 {
        self.arr.as_ptr()
    }
}

JS 側では、インスタンスに対して次の操作をすることで、wasm 内の arr への参照を実体とする配列 arrRef を生成できる。

main.js

const n = instance.get_n();
const ptr = instance.get_ptr();
const arrRef = new Uint8Array(wasm.memory.buffer, ptr, n);

仮に、インスタンス化した構造体 StructExposedToJS の子構造体 ChildStruct が持つ配列を参照しようとした場合、wasm で配列を変更するたびにポインターが変わるようであり、参照するたびに get_ptr() し直し、Uint8Array を生成し直さなければならない。そのくせ、古くなった Uint8Array はガベージコレクションの対象にならないようであり、このためにメモリリークが発生してしまう。親構造体に直に持たせた配列の場合は、始めに一度 Uint8Array を生成すれば、その後、その参照配列を使用し続けられるので、同様のメモリリークは発生しない。気が向いたらこの件に関して詳しく調べてみたい。