確率論的に円周率πを推定してみた

Pythonの標準ライブラリrandomを用いて、確率論的に（厳密に言えばモンテカルロ法的に）円周率を推定してみたという話です。
（読了見込時間：4分）

考え方

xy座標を思い浮かべてください。

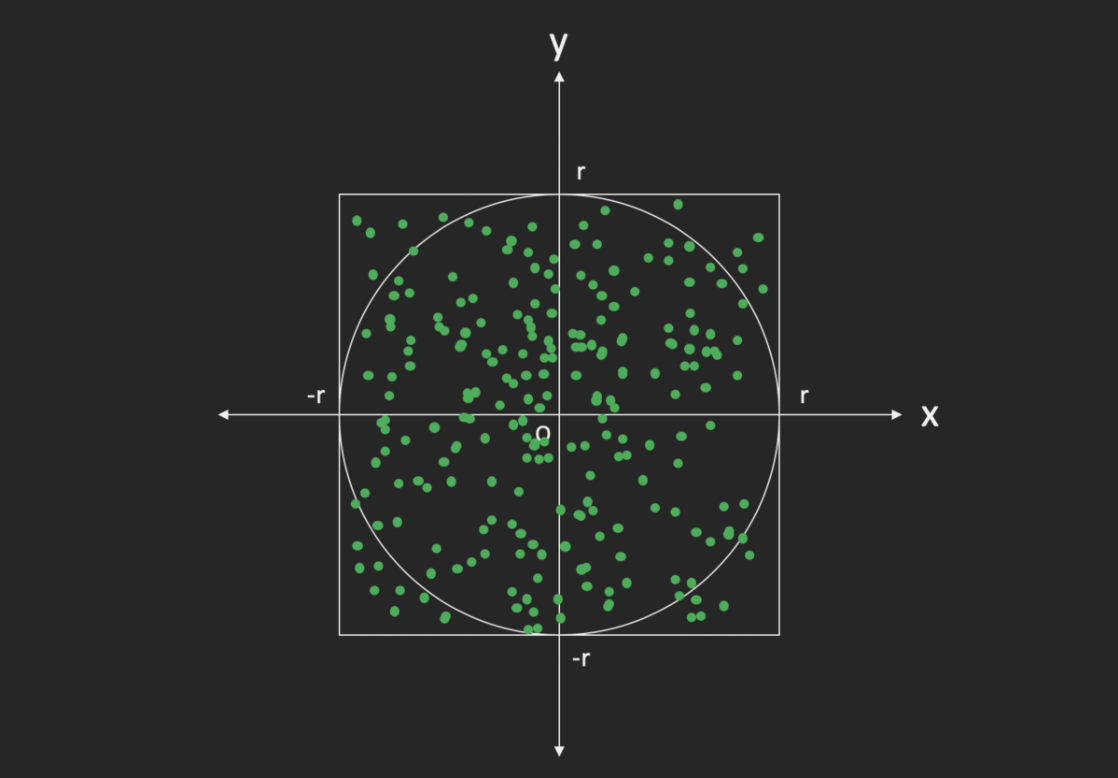
ここに、原点Oを中心とする、半径rの円（Cとします）と、一辺が2rの正方形（Sとします）を描きます。

Sの中に、ひたすらランダムで点（dot）を打ち続けます。

Sの中を埋め尽くすほど点を打ったとき、「Sの中にある点の数：Cの中にある点の数 ≒ Sの面積：Cの面積」と言えます。

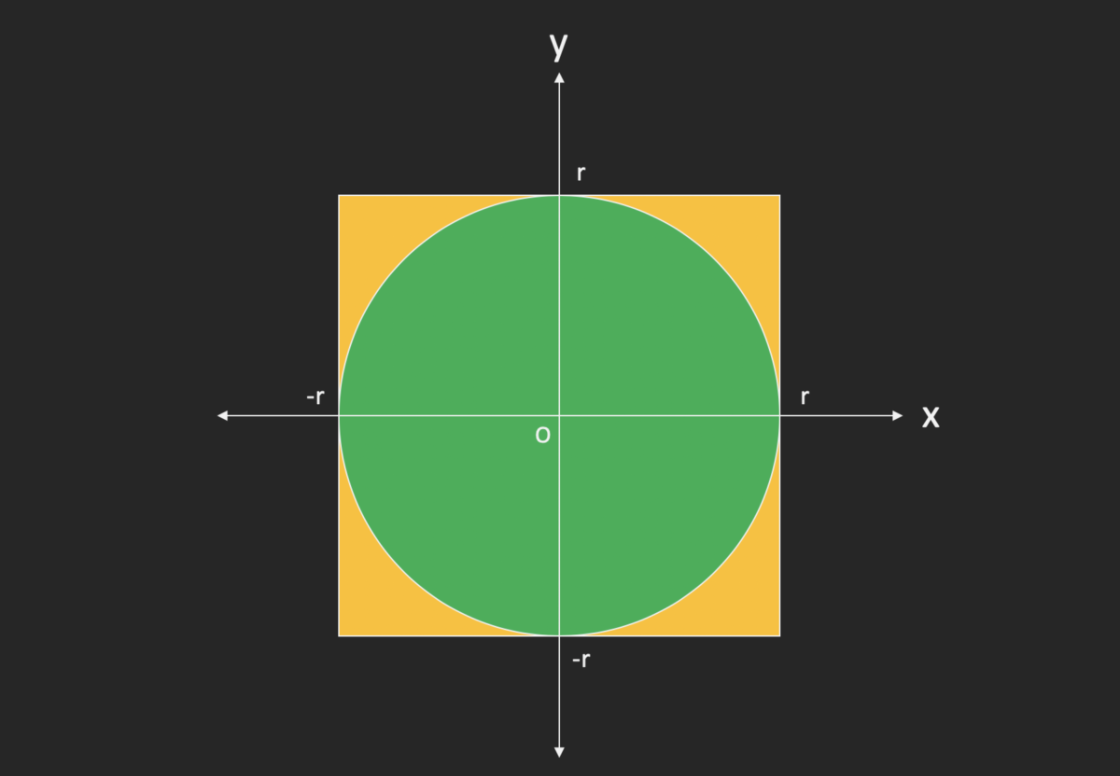
Sの中にある点の数を「s_dot_num」、Cの中にある点の数を「c_dot_num」とおくと、

(c_dot_num) / (s_dot_num)
　= Cの面積 / Sの面積
　= (π * rの2乗) / (2r)の2乗
　= π / 4

となることから、

π = 4 * (c_dot_num) / (s_dot_num)

と定義ができました。
あとは、c_dot_numとs_dot_numをそれぞれ求めることができれば、πの値を推定できます。
（rの値は関係ないようですね）

コード

今回はPythonで書きました。

estimate_pi.py

# 一辺の長さが1の正方形内にランダムにドットを打ち、円周率を推定する。
import random

def estimate_pi(n):
    c_dot_num = 0
    s_dot_num = 0
    for _ in range(n):
        x = random.uniform(0, 1)
        y = random.uniform(0, 1)
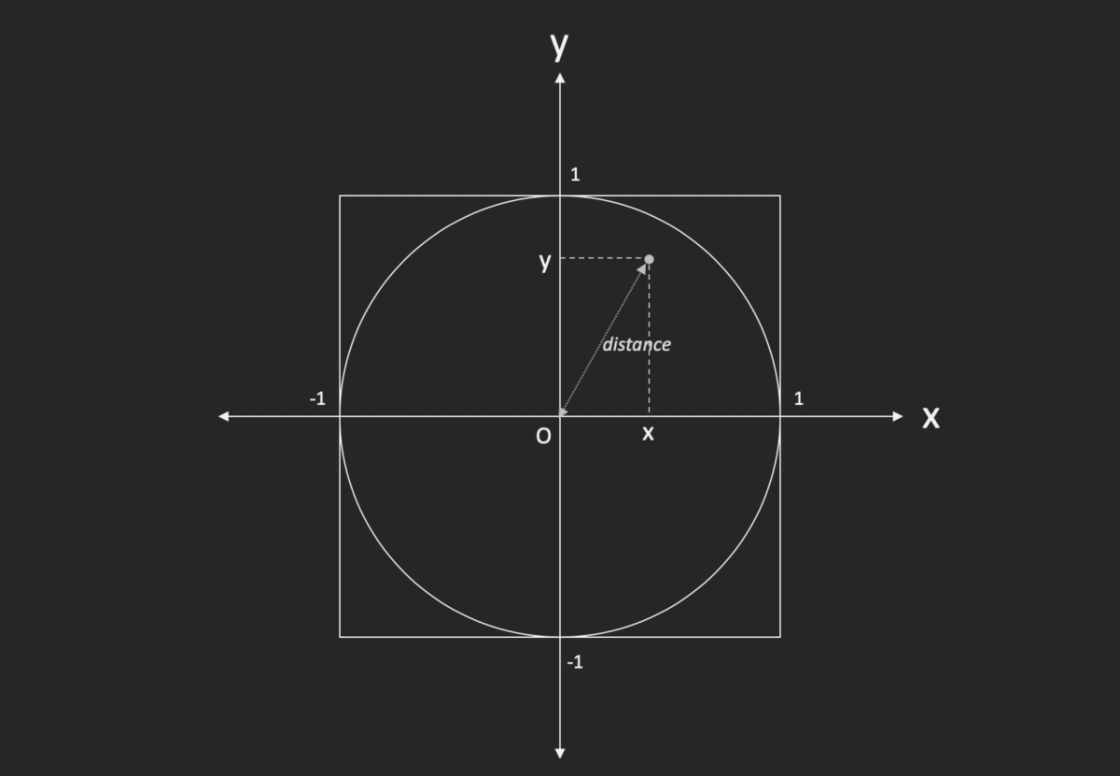
        distance = x**2 + y**2
        if distance <= 1:
            c_dot_num += 1
        s_dot_num += 1
    pi = 4 * c_dot_num / s_dot_num
    return pi

if __name__ == '__main__':
    print('dotが100個のとき、円周率は{}'.format(estimate_pi(100)))
    print('dotが1000個のとき、円周率は{}'.format(estimate_pi(1000)))
    print('dotが10000個のとき、円周率は{}'.format(estimate_pi(10000)))
    print('dotが100000個のとき、円周率は{}'.format(estimate_pi(100000)))

※イメージ

実行結果

1回目

2回目

3回目

おおよそ3.141前後になりました。
試行回数n（=dotを打つ回数）を増やすにつれて、精度が高まっています。

まとめ

今回は、乱数を用いて円周率を推定してみました。
学術的には、乱数を用いて何らかの値を見積もる手法を「モンテカルロ法」と呼ぶそうです。

コード自体は決して難しくはないのですが、初めて知った時に「そういうアプローチがあるのか！」とテンション上がったので備忘録として。