Go to Qiita Advent Calendar 2024 Top
LoginSignup
8
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

BrainPadAdvent Calendar 2024

Day 16
@shichi343

ハイパフォーマンス ベイズA/Bテスト

Last updated at Posted at 2024-12-19

この記事は、BrainPad Advent Calendar 2024の16日目です。

こんにちは。株式会社ブレインパッドでデータサイエンティストをしているshichiです。

ブレインパッドではRtoasterを始めとするSaaSの提供や分析案件のご支援を通じて、多様なA/Bテストを実施する機会があります。

近年、A/Bテストの効果検証手法の1つとしてベイズA/Bテストが注目を集めており、ブレインパッドにおいても独自のベイズA/Bテストパッケージを開発・運用しています。本記事では、社内パッケージの機能のうち、CTR/CVRなどの成功率のベイズA/Bテストの計算アルゴリズムをご紹介します。

ベイズA/Bテストの復習

ベイズA/Bテストでは、成功率を確率変数として扱います。介入群・対照群の成功率の従う確率変数を$X_1, X_2$とし、計算の簡単のため以下のようにベータ分布を事前分布に採用します。

\begin{align}
X_1 &\sim \mathrm{Beta}(\alpha_1,\beta_1) \\
X_2 &\sim \mathrm{Beta}(\alpha_2,\beta_2)
\end{align}

ここで、各群の試行数を$n_1, n_2$、成功数$s_1, s_2$とすると、共役事前分布の性質から、事後分布は以下のように計算することができます。

\begin{align}
X_1 &\sim \mathrm{Beta}(s_1 + \alpha_1, n_1 - s_1 + \beta_1) \\
X_2 &\sim \mathrm{Beta}(s_2 + \alpha_2, n_2 - s_2 + \beta_2)
\end{align}

これらのベータ分布を可視化することで、二群に差があるかどうかを視覚的に確認できます。

image1.png

二群の差を定量的に評価したい場合、A/Bテストでは成功率の相対増加率である「リフト（Lift）」がよく用いられます。ベイズA/Bテストではリフトもまた確率変数であり、$X_1, X_2$の比率を含む以下の式で表されます。

Z = \frac{X_1 - X_2}{X_2} = \frac{X_1}{X_2} - 1

リフトの分布からは、以下のような指標が求められます。

指標 式 解釈
勝利確率 $P(Z > 0)$ 介入群が勝つ確率
期待リフト $\mathbb{E}[Z]$ リフトの期待値
期待損失 $\mathbb{E}_{x \sim Z}[\mathrm{min}(x, 0)]$ 介入群の負けによる損失の期待値

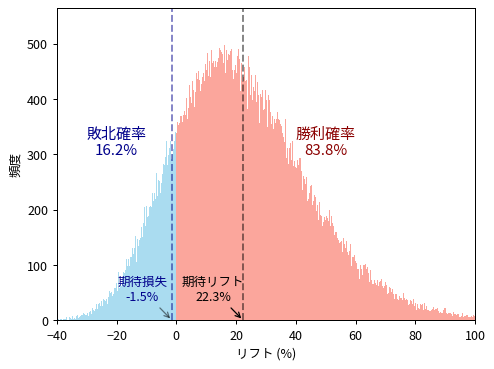
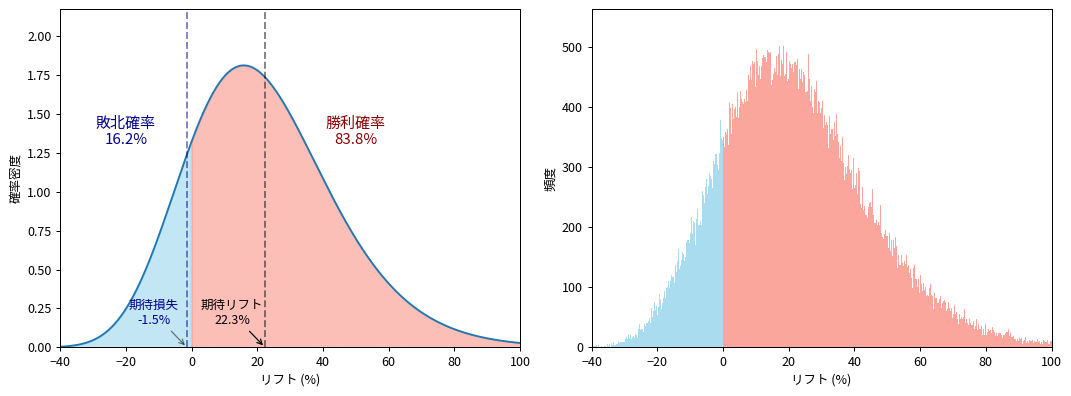
さて、これらの指標を計算するためにはリフトの分布を計算すればよいです。そのためにはベータ分布の比率分布を求める必要があります。多くのブログ記事や書籍では解析的な計算を諦めて、図のようにランダムサンプリングによる近似計算を採用しているように思います。

image2.png

この方法でも実用上は十分事足りるのですが、以下の点が気になります。

  1. 乱数シードに依存して結果が変動する
  2. 十分な精度を得るためには、ある程度のサンプリングが必要
  3. 大量の計算を行う場合に、実行速度がネックになる

実はベータ分布の比率分布は解析的に求められます。以降はリフトの分布や、そこから派生する指標を解析的に計算する方法を紹介します。

リフトの解析計算

リフトを解析的に計算するためには、比率$X_1/X_2$の確率密度関数および累積分布関数が与えられればよいです。以降、ベータ分布の比率が従う確率変数を$Y$とし、以下のように定義します。

Y = \frac{X_1}{X_2} \sim \mathrm{BetaRatio}(\alpha_1,\beta_1,\alpha_2,\beta_2)

リフトの確率密度関数と累積分布関数

$Y$の確率密度関数 $f_Y(x)$ は、超幾何関数 $_2F_1$ を用いて表すことができます。

f_Y(x) =
\begin{cases}
\frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} x^{\alpha_1 - 1} {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + \alpha_2 + \beta_2; x), & \text{if } 0 \leq x \leq 1 \\
\frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{1}{x^{\alpha_2 + 1}} {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_2; \alpha_1 + \alpha_2 + \beta_1; 1/x), & \text{if } 1 < x
\end{cases}

さらに、$Y$の累積分布関数 $F_Y(x)$ は、一般化超幾何関数 $_3F_2$ を用いて表すことができます。

F_Y(x) =
\begin{cases}
\frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{x^{\alpha_1}}{\alpha_1} {}_3F_2(\alpha_1, \alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + 1, \alpha_1 + \alpha_2 + \beta_2; x), & \text{if } 0 \leq x \leq 1 \\
1 - \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{1}{\alpha_2 x^{\alpha_2}} {}_3F_2(\alpha_1, \alpha_1 + \alpha_2, 1 - \beta_2; \alpha_2 + 1, \alpha_1 + \alpha_2 + \beta_1; 1/x), & \text{if } 1 < x
\end{cases}

このように特殊関数を含む形ではありますが、代数計算に持ち込むことができます。これらの式の導出は参考文献[1,2]をご参照ください。

勝利確率

累積分布関数を用いることで、勝利確率 $P(X_1 > X_2)$ を計算できます。$Y = X_1/X_2$ の定義から、$X_1 > X_2$ は $Y > 1$ と同値です。よって、勝利確率は

P(X_1 > X_2) = P(Y > 1) = 1 - F_Y(1)

と表すことができます。一方で敗北確率は、

P(X_1 < X_2) = P(Y < 1) = F_Y(1)

となります。

リフトの期待値

リフトの期待値は、$f_Y(x)$の積分を解かずに2つの成功率の重積分を計算することで簡単に求められます。この計算は非常にエレガントです。

\begin{align}
\mathbb{E}[Y]
&= \int_0^1 \int_0^1 \frac{p_1}{p_2} \mathrm{Beta}(p_1 \mid \alpha_1, \beta_1) \mathrm{Beta}(p_2 \mid \alpha_2, \beta_2) \, dp_1 dp_2 \\
&= \int_0^1 \int_0^1 \frac{p_1}{p_2} \frac{p_1^{\alpha_1 - 1} (1 - p_1)^{\beta_1 - 1}}{\mathrm{B}(\alpha_1, \beta_1)} \frac{p_2^{\alpha_2 - 1} (1 - p_2)^{\beta_2 - 1}}{\mathrm{B}(\alpha_2, \beta_2)} \, dp_1 dp_2 \\
&= \int_0^1 \int_0^1 \frac{p_1^{\alpha_1} (1 - p_1)^{\beta_1 - 1}}{\mathrm{B}(\alpha_1, \beta_1)} \frac{p_2^{\alpha_2 - 2} (1 - p_2)^{\beta_2 - 1}}{\mathrm{B}(\alpha_2, \beta_2)} \, dp_1 dp_2 \\
&= \frac{\alpha_1}{\alpha_1 + \beta_1} \frac{\alpha_2 + \beta_2 - 1}{\alpha_2 - 1} \int_0^1 \int_0^1 \frac{p_1^{\alpha_1} (1 - p_1)^{\beta_1 - 1}}{\mathrm{B}(\alpha_1 + 1, \beta_1)} \frac{p_2^{\alpha_2 - 2} (1 - p_2)^{\beta_2 - 1}}{\mathrm{B}(\alpha_2 - 1, \beta_2)} \, dp_1 dp_2 \\
&= \frac{\alpha_1}{\alpha_1 + \beta_1} \frac{\alpha_2 + \beta_2 - 1}{\alpha_2 - 1} \int_0^1 \int_0^1 \mathrm{Beta}(p_1 \mid \alpha_1 + 1, \beta_1) \mathrm{Beta}(p_2 \mid \alpha_2 - 1, \beta_2) \, dp_1 dp_2 \\
&= \frac{\alpha_1}{\alpha_1 + \beta_1} \frac{\alpha_2 + \beta_2 - 1}{\alpha_2 - 1}
\end{align}

残った積分はベータ分布の同時分布の積分であることから1になります。また、途中でベータ関数の漸化的性質

\mathrm{B}(\alpha+1, \beta) = \frac{\alpha}{\alpha+\beta} \mathrm{B}(\alpha, \beta)

を用いています。

期待損失

ここでは期待損失を以下の損失関数

L(p_1,p_2) =
\begin{cases}
p_1/p_2 & \text{if } p_1 < p_2 \\
0 & \text{if } p_1 > p_2
\end{cases}

の期待値で定義します。これも2つの成功率の重積分で計算できます。損失関数の形状から$p_1 < p_2$となる領域での積分を考えればよく、

\begin{align}
\mathbb{E}[L(p_1,p_2)]
&= \int_0^1 \int_0^{p_2} \frac{p_1}{p_2} \mathrm{Beta}(p_1 \mid \alpha_1, \beta_1) \mathrm{Beta}(p_2 \mid \alpha_2, \beta_2) \, dp_1 dp_2 \\
&= \frac{\alpha_1}{\alpha_1 + \beta_1} \frac{\alpha_2 + \beta_2 - 1}{\alpha_2 - 1} \int_0^1 \int_0^{p_2} \mathrm{Beta}(p_1 \mid \alpha_1 + 1, \beta_1) \mathrm{Beta}(p_2 \mid \alpha_2 - 1, \beta_2) \, dp_1 dp_2 \\
&= \frac{\alpha_1}{\alpha_1 + \beta_1} \frac{\alpha_2 + \beta_2 - 1}{\alpha_2 - 1} P(X_1 < X_2) \\
&= \frac{\alpha_1}{\alpha_1 + \beta_1} \frac{\alpha_2 + \beta_2 - 1}{\alpha_2 - 1} F_Y(1)
\end{align}

と計算できます。すなわち期待損失は、リフトの期待値と敗北確率の積で表されることがわかります。

リフトの分布の可視化

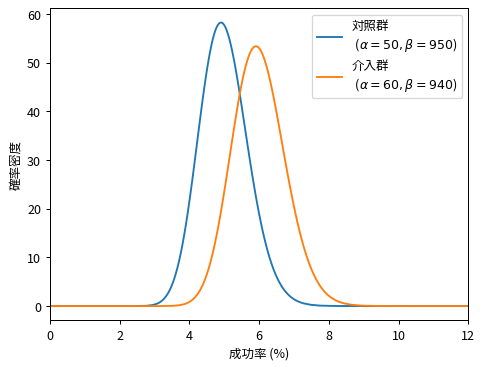
リフトの分布を、ランダムサンプリングによるヒストグラムと超幾何関数による解析解で比較してみます。計算条件は $\alpha_1=60,\beta_1=940,\alpha_2=50,\beta_2=950$ としています。

image3.png

リフトの分布は最頻値に対して左右対称ではなく、正の範囲側で裾野が持ち上がっていることが分かります。また、期待リフトが最頻値よりも大きいことが明確に分かります。

勝利確率の高速計算

ベータ関数の有限和による計算

ここまでの計算で、累積分布関数の特殊値 $F_Y(1)$ を用いて、勝利確率や期待損失を解析的に計算できることがわかりました。しかし、実際にはパラメータ $\alpha_1, \beta_1, \alpha_2, \beta_2$ が大きくなるにつれて $_3F_2$ の収束性が悪くなり必要計算量が大きくなるため、実用に耐える計算は難しくなります。そのために $_3F_2$ を排除した計算方法を紹介します。

$F_Y(1)$は敗北確率であるため、2つの成功率の重積分で表現することもできます。

F_Y(1) = P(X_1 < X_2) = \int_0^1 \int_0^{p_2} \mathrm{Beta}(p_1 \mid \alpha_1, \beta_1) \mathrm{Beta}(p_2 \mid \alpha_2, \beta_2) \, dp_1 dp_2

この重積分を解くと、パラメータの対称性から、以下の4つの形式が得られます。いずれもベータ関数を項に含む有限和で計算できることが分かります。

\begin{align}
F_Y(1)
&= \sum_{i=0}^{\alpha_2 - 1} \frac{\mathrm{B}(\alpha_1 + i, \beta_2 + \beta_1)}{(\beta_2 + i) \mathrm{B}(1 + i, \beta_2) \mathrm{B}(\alpha_1, \beta_1)} \\
&= 1 - \sum_{i=0}^{\alpha_1 - 1} \frac{\mathrm{B}(\alpha_2 + i, \beta_1 + \beta_2)}{(\beta_1 + i) \mathrm{B}(1 + i, \beta_1) \mathrm{B}(\alpha_2, \beta_2)} \\
&= \sum_{i=0}^{\beta_1 - 1} \frac{\mathrm{B}(\beta_2 + i, \alpha_1 + \alpha_2)}{(\alpha_1 + i) \mathrm{B}(1 + i, \alpha_1) \mathrm{B}(\alpha_2, \beta_2)} \\
&= 1 - \sum_{i=0}^{\beta_2 - 1} \frac{\mathrm{B}(\beta_1 + i, \alpha_1 + \alpha_2)}{(\alpha_2 + i) \mathrm{B}(1 + i, \alpha_2) \mathrm{B}(\alpha_1, \beta_1)}
\end{align}

実装時には $\alpha_1, \alpha_2, \beta_1, \beta_2$ のうち最小の値を和の項数として選択することで、計算量を最小化します。これらの式の導出は参考文献[3]で解説されています。

ベータ関数の有限和の漸化的計算

上記の式ではベータ関数を繰り返し計算する必要があるため、パラメータが大きい場合は依然として計算コストが高くなります。これを解消するために、これらのベータ関数のパラメータが1ずつ異なることとベータ関数の漸化的性質を利用し、隣接項の差分のみを計算する形式に変換します。ここでは $\alpha_2$ に関する有限和の式について過程を示します。

\begin{align}
F_Y(1)
&= \sum_{i=0}^{\alpha_2 - 1} \frac{\mathrm{B}(\alpha_1 + i, \beta_1 + \beta_2)}{(\beta_2 + i) \mathrm{B}(1 + i, \beta_2) \mathrm{B}(\alpha_1, \beta_1)} \\
&= \sum_{i=0}^{\alpha_2 - 1} \left[ \frac{\mathrm{B}(\alpha_1, \beta_1 + \beta_2)}{(\beta_2 + i) \mathrm{B}(1, \beta_2) \mathrm{B}(\alpha_1, \beta_1)} \prod_{j=0}^{i-1} \frac{(\alpha_1 + j)(1 + j + \beta_2)}{(\alpha_1 + j + \beta_1 + \beta_2)(1 + j)} \right] \\
&= \frac{\mathrm{B}(\alpha_1, \beta_1 + \beta_2)}{\mathrm{B}(\alpha_1, \beta_1)} \sum_{i=0}^{\alpha_2 - 1} \left[ \frac{\beta_2}{\beta_2 + i} \prod_{j=0}^{i-1} \frac{(\alpha_1 + j)(1 + j + \beta_2)}{(\alpha_1 + j + \beta_1 + \beta_2)(1 + j)} \right]
\end{align}

見通しを立てるために、以下のようにベクトルを定義します。

\begin{align}
u_{i} &= \frac{\beta_2}{\beta_2+i}
& v_j &= \frac{(\alpha_1 + j)(1 + j + \beta_2)}{(\alpha_1 + j + \beta_1 + \beta_2)(1 + j)} \\
\mathbf{u} &=
\begin{pmatrix}
 u_0 \\ u_1 \\ u_2 \\ \vdots \\ u_{\alpha_2-1}
\end{pmatrix} &
\mathbf{v} &=
\begin{pmatrix}
 1 \\ v_0 \\ v_0 v_1 \\ \vdots \\ v_0 v_1 \cdots v_{\alpha_2-2}
\end{pmatrix}
\end{align}

これらを用いると $F_Y(1)$ は以下のようにベクトルの内積で表現できます。

F_Y(1) = \frac{\mathrm{B}(\alpha_1, \beta_1 + \beta_2)}{\mathrm{B}(\alpha_1, \beta_1)}
\mathbf{u}^{\top} \mathbf{v}

この形式では、ベータ関数の計算は初項のみで済み、残りの項は $\mathbf{v}$ における累積的な要素計算に帰着するため、効率的になります。

精度・速度比較

実験条件

勝利確率の計算精度・速度を、従来法（ランダムサンプリング）と解析解で比較してみます。具体的には以下の5通りで比較してみます。

  1. ランダムサンプリング（100万回）
  2. ランダムサンプリング（1万回）
  3. 一般化超幾何関数による解析解
  4. ベータ関数の有限和による計算
  5. ベータ関数の有限和の漸化的計算

分布のパラメータは $\alpha_1 = \beta_1 = \alpha_2 = \beta_2 = 1000$ とします。このときの真の勝利確率は厳密に50%になります。

実験結果

結果は以下になります。サンプリング法では乱数シードを10通り試したときの勝利確率の最大・最小範囲を示しています。平均計算時間はIPythonの%timeitコマンドを利用しました。漸化的計算からのスピードアップ率も載せています。

計算法 サンプル数 勝利確率 [%] 平均計算時間 [ms] Speed up
サンプリング 1,000,000 49.94 - 50.09 127 ms 6876.1x
サンプリング 10,000 48.88 - 50.67 1.3 ms 71.0x
一般化超幾何関数 - 50.00 11.0 ms 590.2x
有限和計算 - 50.00 0.073 ms 3.9x
漸化的計算 - 50.00 0.0019 ms -

この結果から、勝利確率を解析的に解くことで、解の厳密性と計算速度を両立した、まさにハイパフォーマンスなベイズA/Bテストを実現できることが分かります。

サンプルコード

勝利確率を計算する実装のサンプルコードです。実装はPython(numpy, scipy)で行い、一部numbaによるJITコンパイルを行っています。

実装では、ベータ関数のパラメータが大きい場合の発散に対処するため、対数空間で計算を行う必要があります。また、一般化超幾何関数の計算には任意精度演算ライブラリであるmpmathを用いています。パラメータが大きいときに収束性の悪化が発生した場合は、追加の引数で精度等を変更できます。

beat_probability.py
import math

import mpmath
import numpy as np
from numba import njit
from scipy import stats
from scipy.special import betaln


def cdf1_sampling(a1, b1, a2, b2, size, seed):
    np.random.seed(seed)
    samples1 = stats.beta.rvs(a1, b1, size=size)
    samples2 = stats.beta.rvs(a2, b2, size=size)
    return np.mean(samples1 < samples2)


def cdf1_hyp3f2(a1, b1, a2, b2):
    hyp = mpmath.hyp3f2(a1, a1 + a2, 1 - b1, a1 + 1, a1 + a2 + b2, 1)
    return math.exp(betaln(a1 + a2, b2) - betaln(a1, b1) - betaln(a2, b2) + mpmath.log(hyp)) / a1


def cdf1_sigma(a1, b1, a2, b2):
    i = np.arange(a2)
    return np.sum(np.exp(betaln(a1 + i, b1 + b2) - np.log(b2 + i) - betaln(1 + i, b2) - betaln(a1, b1)))


@njit
def boost(a1, b1, a2, b2, coefln_beta):
    i = np.arange(a2 - 1)
    u = coefln_beta + np.log(b2) - np.log(b2 + 1 + i)
    v = np.cumsum(np.log((b2 + 1 + i) * (a1 + i) / (b2 + a1 + b1 + i) / (1 + i)))
    return np.exp(coefln_beta) + np.sum(np.exp(u + v))


def cdf1_sigma_expansion(a1, b1, a2, b2):
    coefln_beta = betaln(a1, b2 + b1) - betaln(a1, b1)
    return boost(a1, b1, a2, b2, coefln_beta)


alpha1, beta1, alpha2, beta2 = 1000, 1000, 1000, 1000

result1 = cdf1_sampling(alpha1, beta1, alpha2, beta2, size=1_000_000, seed=42)
print("サンプリング", result1)

result2 = cdf1_hyp3f2(alpha1, beta1, alpha2, beta2)
print("一般化超幾何関数", result2)

result3 = cdf1_sigma(alpha1, beta1, alpha2, beta2)
print("有限和計算", result3)

result4 = cdf1_sigma_expansion(alpha1, beta1, alpha2, beta2)
print("漸化的計算", result4)

まとめ

ベイズA/Bテストにおけるリフトの分布を、超幾何関数を用いて解析的に計算する方法を紹介しました。

勝利確率の計算においては、ベータ関数の漸化的性質を利用することで、正確かつ高速に計算できます。また、解析解を用いることで、乱数に依存しない再現性の高い結果を得ることができます。

参考文献

[1] On the ratio of Beta-distributed random variables - Some Weekend Reading
[2] Pham-Gia, T. (2000). Distributions of the ratios of independent beta variables and applications. Communications in Statistics - Theory and Methods, 29(12), 2693–2715. https://doi.org/10.1080/03610920008832632
[3] Formulas for Bayesian A/B Testing - Evan Miller

8
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?