はじめに
- huggingfaceなどで公開されているニューラルネットワークのプログラムを見ると、"logit"とという変数が出てくる
- ここでの"logit"は何を意味しているのか?数学的意味があるのか?
数学のlogitの定義(初心者が混乱するやつ)
wikipediaの説明を読んでみると、次のようなことが書かれている。
ロジット(英: logit)とは、0から1の値をとるp に対し
$\displaystyle \operatorname {logit} (p)=\log \left({\frac {p}{1-p}}\right)=\log(p)-\log(1-p)$
で表される値をいう。p を変数とするロジット関数とも呼ばれる。
ロジット関数はロジスティック関数
$\displaystyle \operatorname {expit} (\alpha )={\frac {1}{1+e^{-\alpha }}}={\frac {e^{\alpha }}{1+e^{\alpha }}}$
の逆関数であり、特に確率論と統計学で多く用いられる。
初心者はここで死亡する。
ただ、ここでヒントになりそうなポイントは次の事項だ。
- logitは確率値に関係する
- 確率値に変換する関数(ロジスティック関数)の逆変換(逆関数)である
ニューラルネットワークで使われるlogitの説明
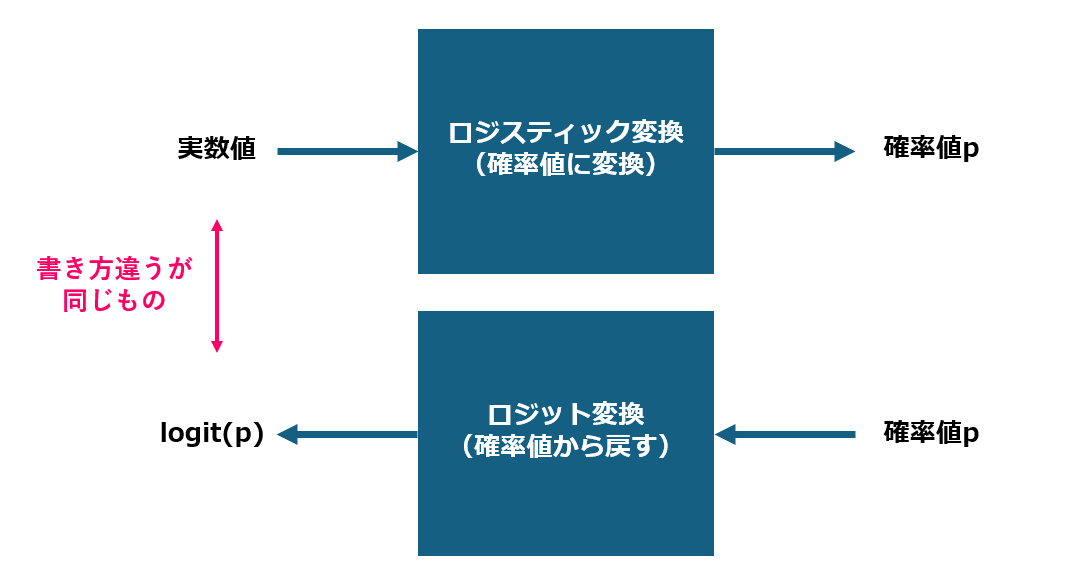
前節の説明を整理すると、次のような図で書けそうだ。
ここまで整理すると、実はすぐさま結論がわかる。
ニューラルネットワークで使われる変数"logit"とは図のようなイメージだ。

すなわち、確率値に変換をかける直前の、変換していない値を単にlogitと呼んでいるだけだ。
おわりに
- 案外説明されてない気がしたので記事書きました
- こういう「案外説明されてないもの」は結構多い気がする