はじめに
今回は、数あるインデックスの中でも最も基本かつポピュラーなB-Treeインデックスについてまとめていきます。
インデックスとは
インデックスとは、テーブル内の特定のレコード(行)へのポインタです。インデックスを使用することで、高速にデータを検索することができ、データベースのパフォーマンスが向上します。
インデックスは、書籍の索引のようなものです。500ページある書籍から「データベース」という単語を探すために1ページ目から順番に探すとかなりの労力と時間がかかります。しかし、本の巻末にある索引で「データベース」という単語が記載されているページを調べて、直接そのページを見にいくことができれば、効率が大幅に上がります。データベースのインデックスもこれと同じことをしています。
なぜインデックスが必要なのか
インデックスを使用しない場合
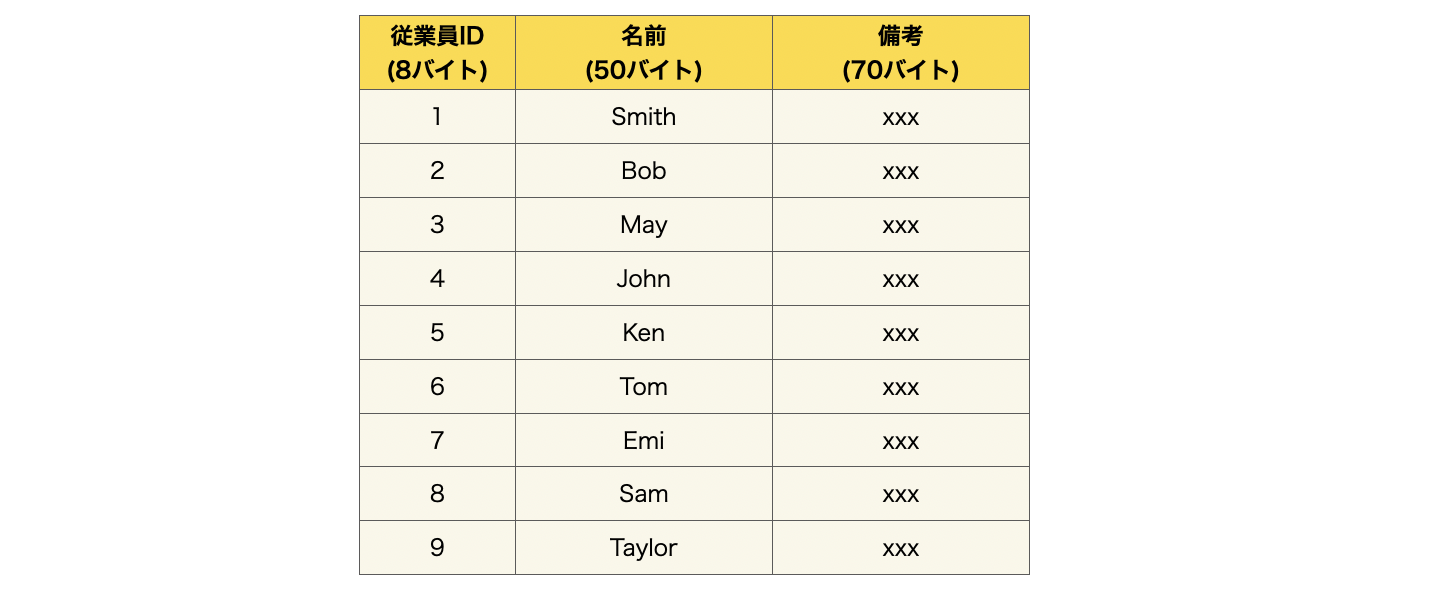
以下の従業員テーブルを使用して、インデックスを使用しない場合を見ていきます。
従業員テーブルにおいて、1人の従業員(各レコード)のデータサイズは、128バイトになります。そして、データベースのストレージとしてHDD(ハードディスクドライブ)を使用する場合、その各ブロックに格納可能な一般的なデータサイズは、512バイトになります。
ブロックとは、データベースがディスク上でデータを読み書きする際の最小単位です。
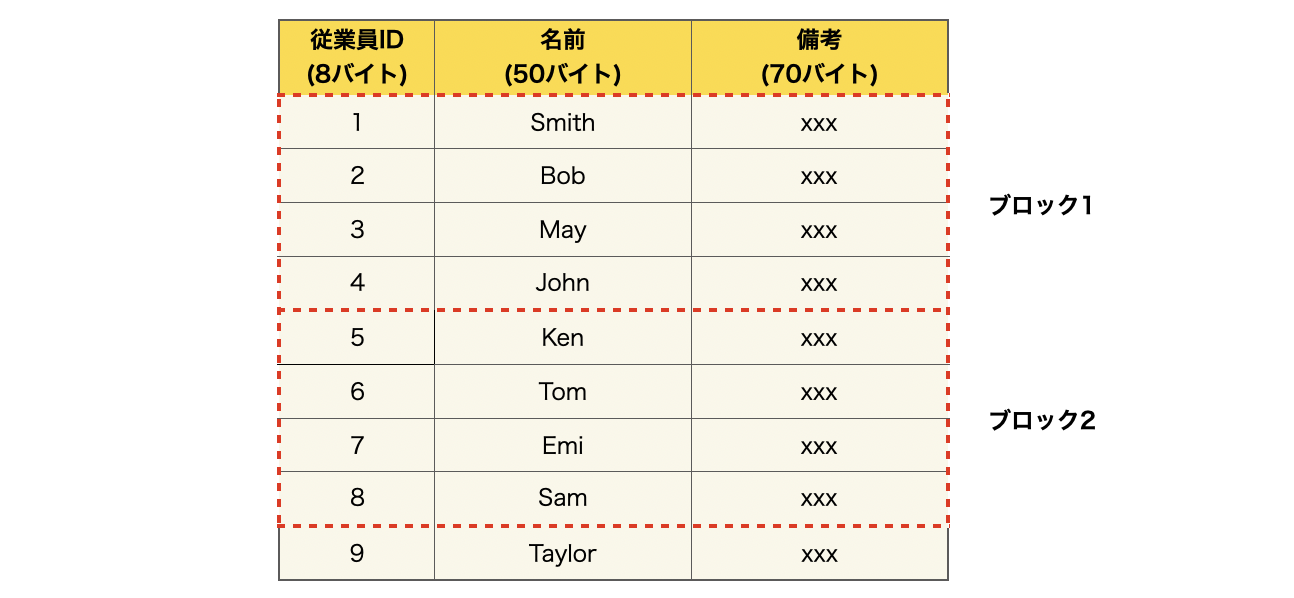
この時、HDDの各ブロックには4レコード分のデータを格納することができます。
512byte / 128byte = 4 (ブロックサイズ/レコードサイズ)
つまり、従業員テーブルの1~4行目はブロック1に、5~8行目はブロック2に格納されます。
仮に、従業員が1000人いるとすると、250個のブロックが必要になります。この時、データベースから1人の従業員、つまり1レコードを検索するために、最大で250個全てのブロックを調べる必要があります。
インデックスを利用することで、より効率的に従業員を検索することができます。
インデックスを使用する場合
従業員テーブルの従業員IDに対してインデックスを貼り、キーとポインタを持つインデックステーブルを新たに作成します。各ポインタは、従業員テーブルの対応するレコードを指します。
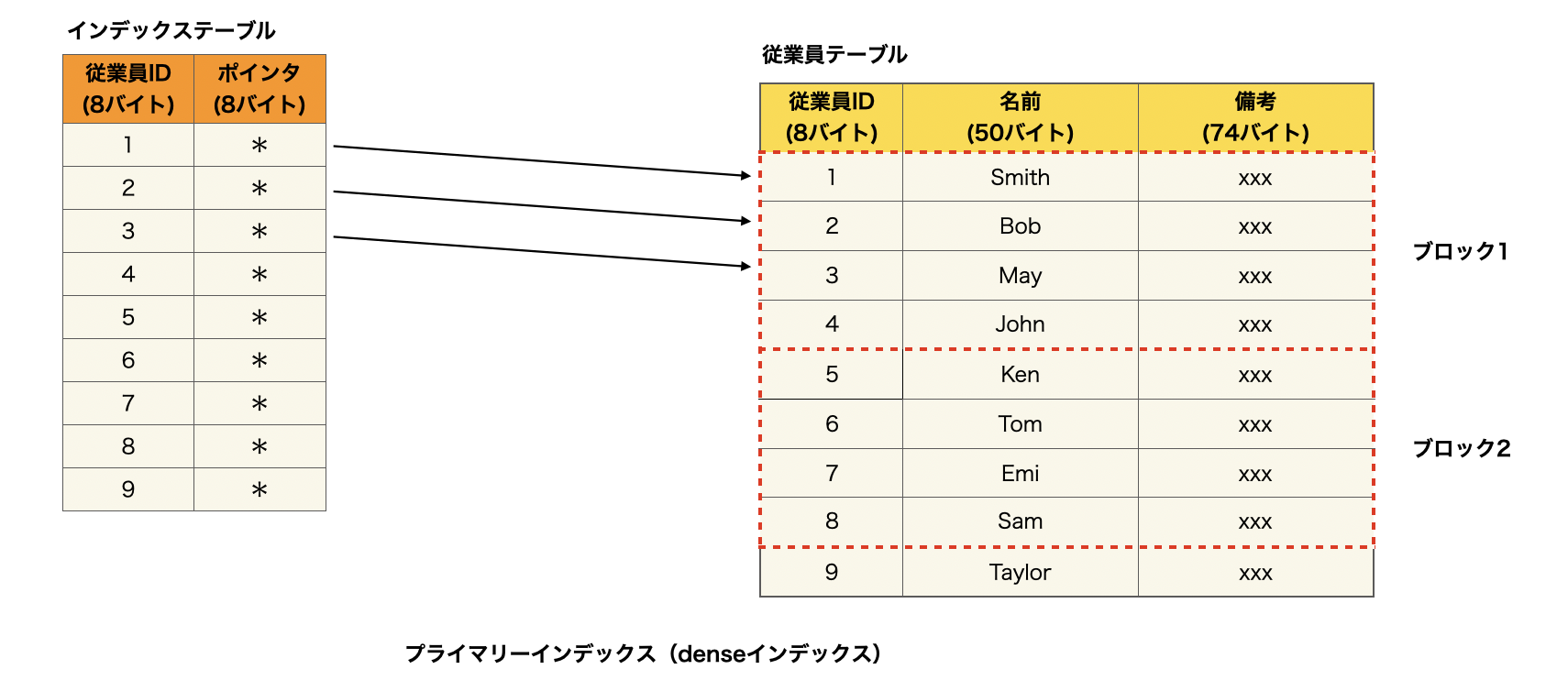
インデックステーブルの各レコードのデータサイズは16バイトであるため、HDDの各ブロックに32個のレコードを保存することができます。
512byte / 16byte = 32 (ブロックサイズ/レコードサイズ)
インデックステーブルの1000個のレコード(従業員1000人分)を保存するためには、32個のブロックが必要になります。
1000records / 32records = 31.25 (総レコード数/ブロック内に保存可能なレコード数)
インデックスなしの場合、つまり従業員テーブルをフルスキャンして1人の従業員を探すためには、最大で250個のブロックを確認する必要がありました。しかし、インデックスを導入することで探索するブロック数が32個に減少しました。
B-Treeインデックス
インデックステーブルを作成することでデータ検索時のパフォーマンスが向上しましたが、それでも最悪時には全てのレコードを調べる必要があります。さらに効率よくデータ検索を行うために、多くのデータベースではB-Treeインデックスが使用されます。
B-Treeインデックスの性質
B-Tree(Balanced-Tree、B木)は、以下の特徴をもつ平衡木です。
- 各ノードは、キーと実データ(レコード)へのポインタ、子ノードへのポインタを持つ
- ノード内のキーは昇順にソートされる
- 親ノードのキー値は左の子ノードのキー値より大きく、右の子ノードのキー値より小さい
- リーフノードは全て同じ階層に存在する
B+ Treeでは、リーフノードのみが実データへのポインタを持ちます。
- 1つのノードは、最小で
t個、最大でm個の子ノードを持つ(2 <= t <= m) -
t <= 1つのノードが持つ子ノード数 <= 2t(2t = m) -
t - 1 <= 1つのノードが持つキー数 <= 2t - 1
→ ルートノードは例外で1個以上のキーを持つ
B-Treeの1つのノードが保持する最小の子ノード数は、最小次数(minimum degree)と呼ばれるtというパラメータを使用して決定されます。tの値はブロックサイズに依存しますが、必ずt >= 2となります。
また、最大でm個の子ノードを持つことができるB-Treeをm階のB-Treeといいます。
B-Treeのノード内の構成
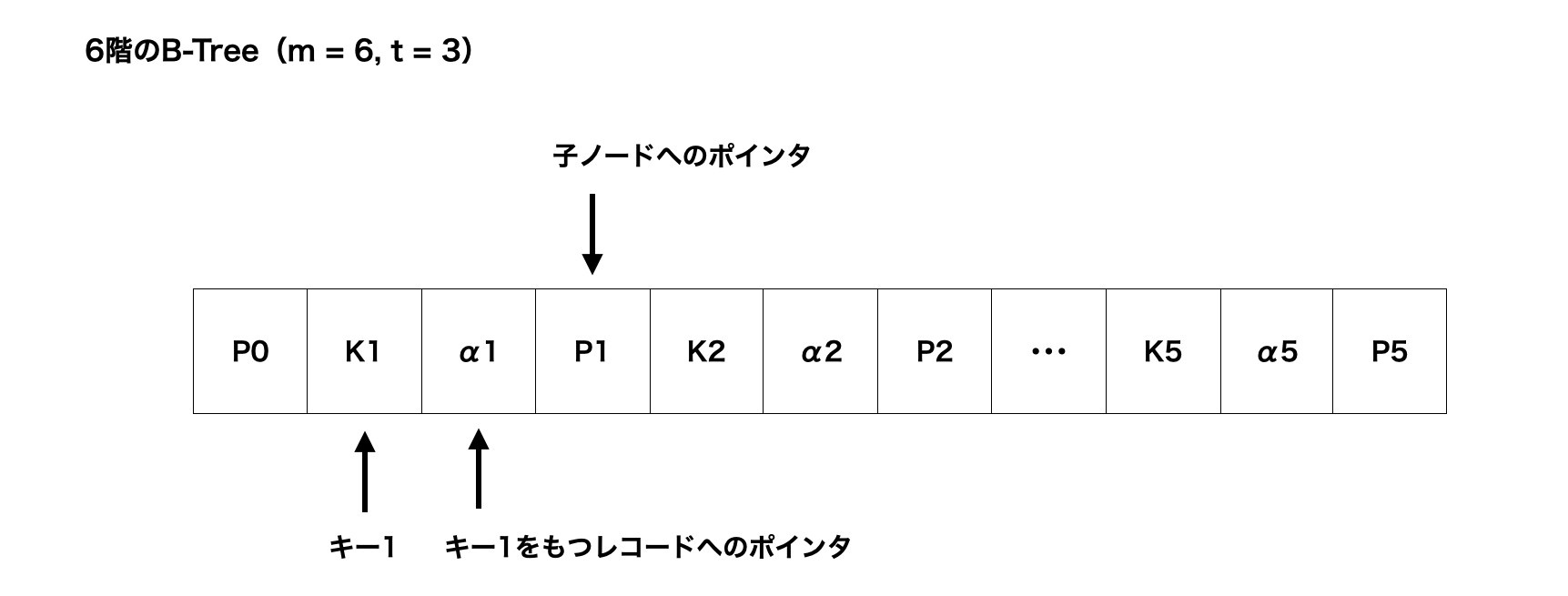
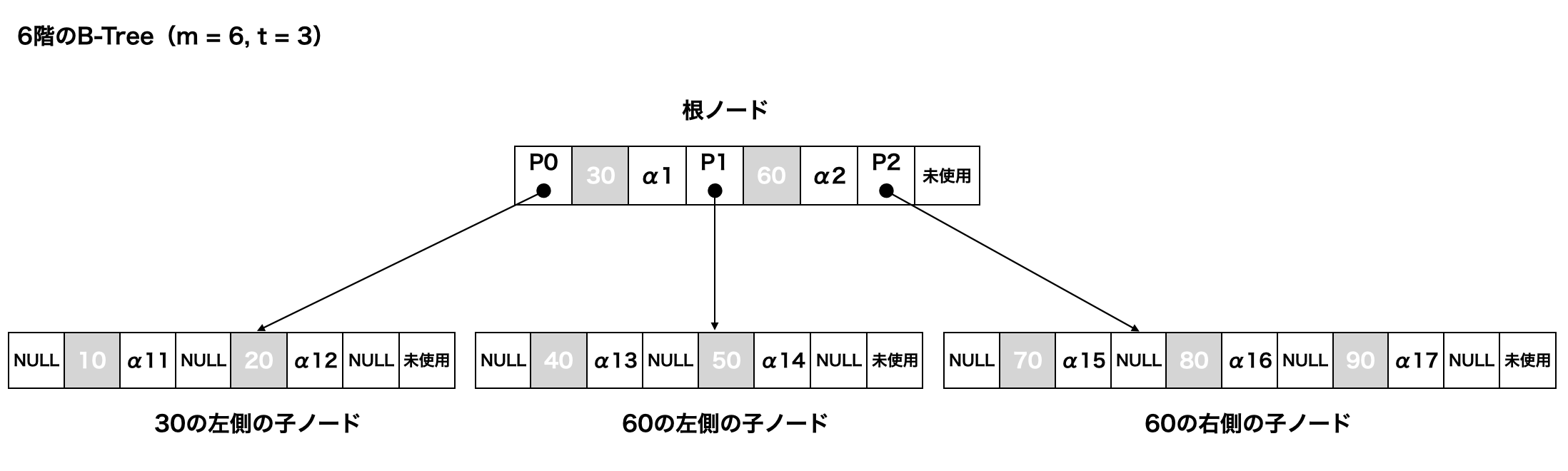
以下は、6階のB-Tree(m = 6, t = 3)の各ノード内の構成です。
Pは子ノードへのポインタ、Kはキー、αは実データ(レコード)へのポインタです。
B-Treeの構成
6階のB-Treeを図示してみます。
この時、m = 6, t = 3 よりB-Treeの条件は以下になります。
- 各ノード内の最小キー数:2
- 各ノード内の最大キー数:5
- 各ノード内の最小子ノード数:3
- 各ノード内の最大子ノード数:6
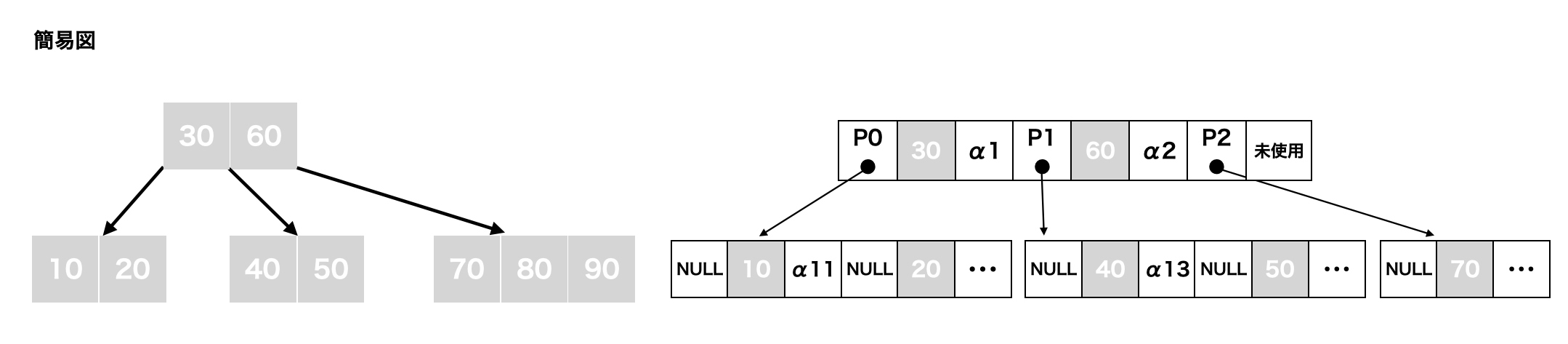
今後は、以下左側の簡易図(右側の省略形)をメインで使用していきます。
検索
ルートノードからスタートし、目的のキーを発見するまで子ノードを再帰的に探索していきます。
- ルートノードからスタートし、ノード内の昇順に並んでいるキーと目的のキーを順に比較していく
- 目的のキーが存在する場合は、ノードを返す。存在しない場合は、目的のキーより大きなキー値が見つかったら、その左側の子ノードに進み、見つからなかったら一番右側の子ノードに進む
- 葉ノードに到達するまで1-2を繰り返し、目的のキーが存在する場合は、ノードを返す。存在しない場合は、NULLを返す
具体例
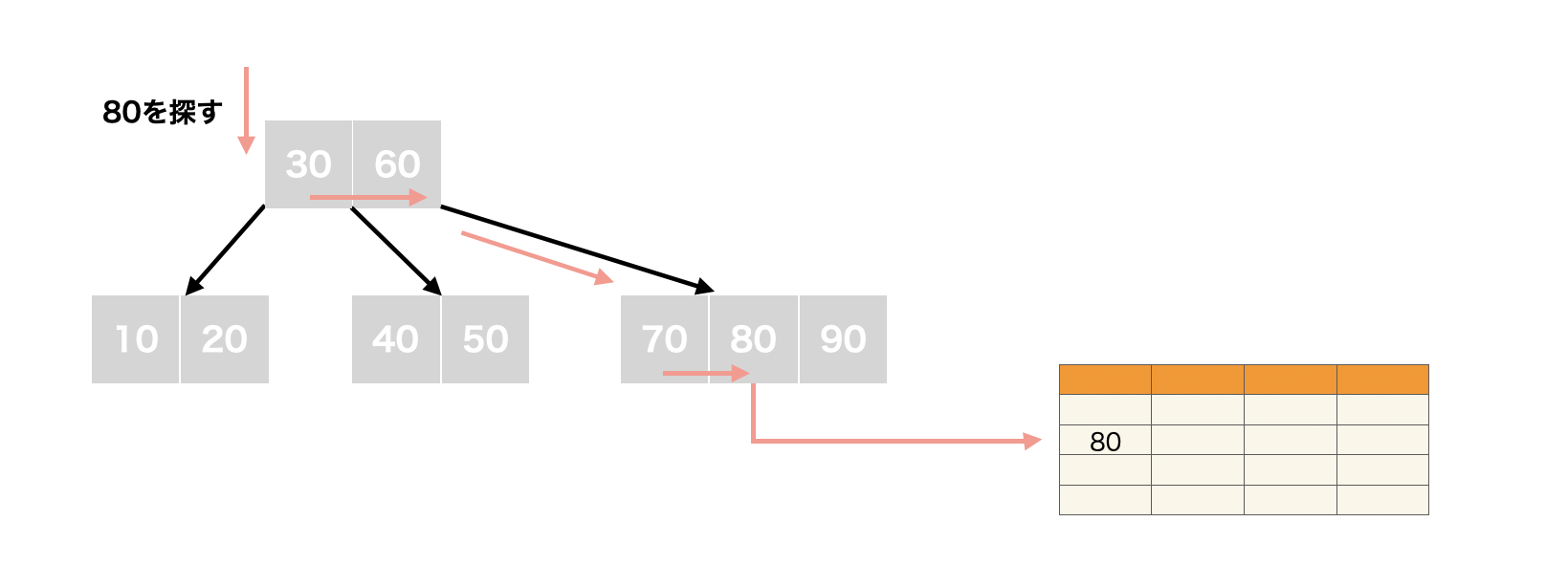
先ほどの6階のB-Treeにて、50という値を探索する場合を考えてみます。
- ルートノード内のキー値
30,60と50を順に比較していく - ルートノードには、目的のキーが存在しないので、50より大きいキー値である60の左側の子ノード(P1)に進む
- 子ノード内でキー値50が見つかったので、子ノードを返す
挿入
挿入の場合も検索と同じく、ルートノードから始めて、子ノードに向かって挿入する場所を探していきます。挿入は必ず葉ノードに行われます。
1-1. 木が空の場合、ルートノードを作成しキーとデータ(ポインタ)を挿入する
1-2. ルートノードがすでに存在する場合、キーの比較を行い、挿入すべき位置を決定する。挿入キーが現在のキーより小さい場合は左、大きい場合は右の子ノードに進む。これを葉ノードまで繰り返す
2. 葉ノードに到達したら、ノード内のキーが昇順を保つようにキーとデータを挿入する
3. 葉ノードがオーバーフローする場合、ノードを中央で分割し、中央値となるキーを親ノードに移動させる。その後、残りの要素を左右の子ノードに分配する
具体例
キー(10, 20, 30, 40, 50, 60, 70, 80, 90)を順番に挿入していく様子を見ていきたいと思います。今回も、m = 6, t = 3とします。
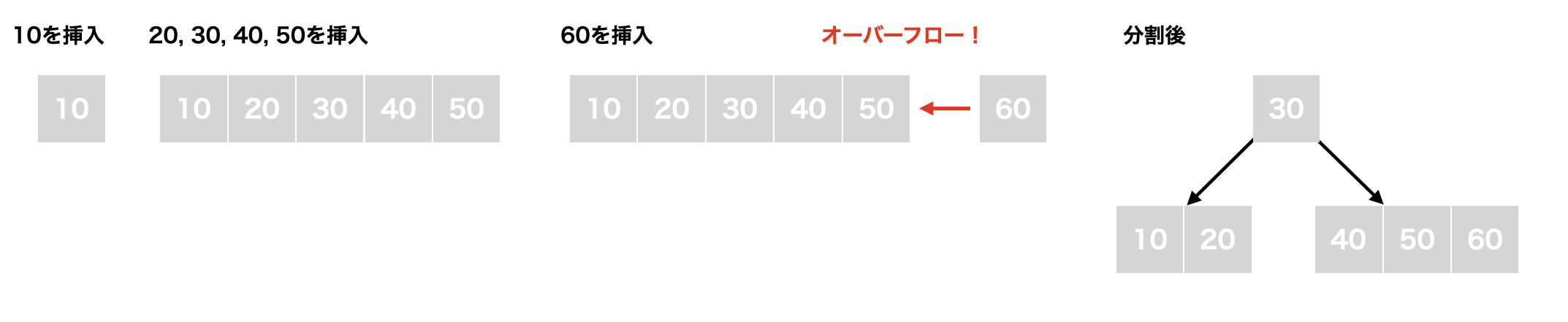
- ルートノードに
10を挿入する -
2t - 1 = 5よりルートノードは5個のキーを持つことができるため、20, 30, 40, 50を順に追加していく - ルートノードに
60を挿入する。ルートノード内のキー数は6になり、オーバーフローするため分割が必要になる。新たに作成した親ノードに10, 20, 30, 40, 50, 60の中央値である30を追加して、その左の子ノードに10, 20、右の子ノードに40, 50, 60を設定する
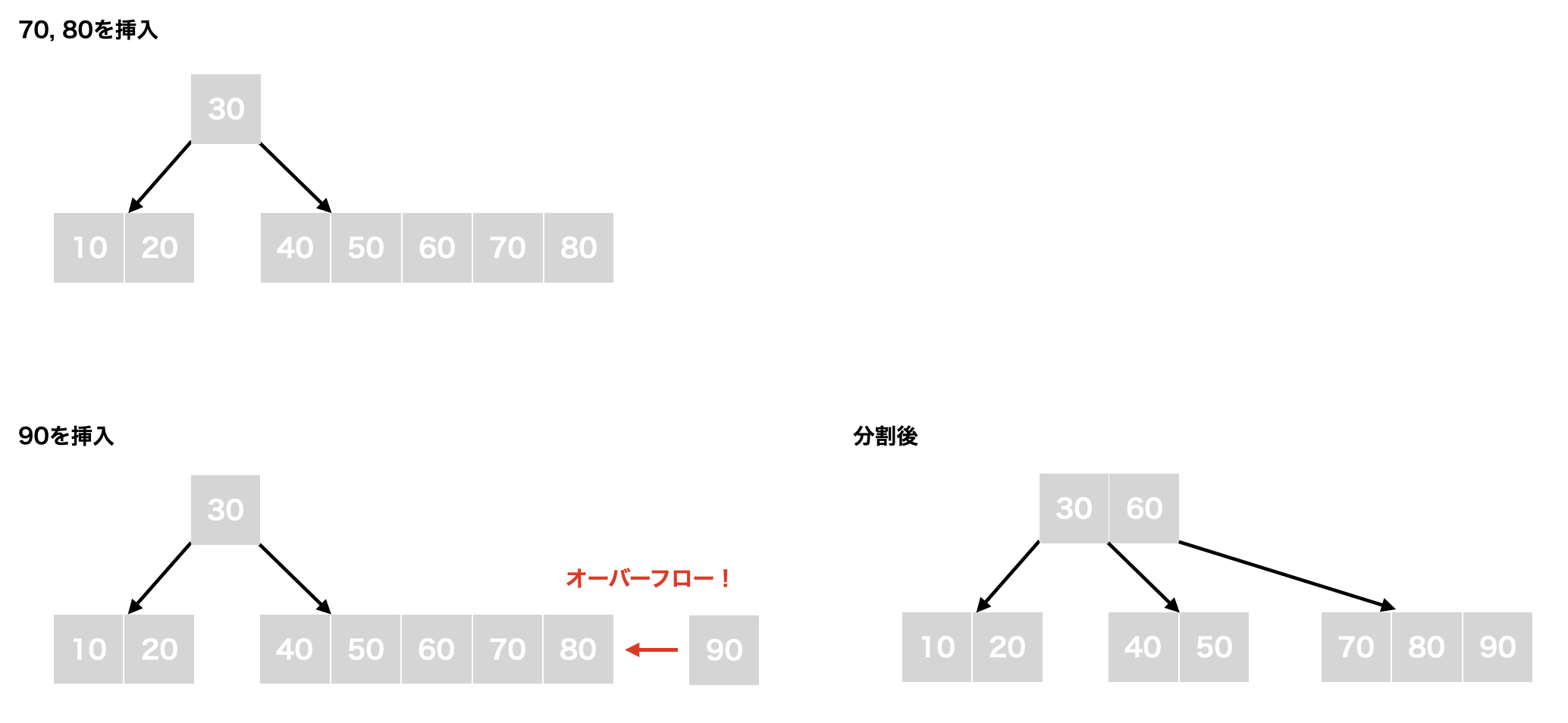
3. 70, 80を右の子ノードに追加する
4. 90を追加するとオーバーフローが発生するため、分割を行う。40, 50, 60, 70, 80, 90の中央値である60を親ノードであるルートノードに追加する。そして、60の左の子ノードに40, 50、右の子ノードに70, 80, 90を設定する
削除 (対象キーが葉ノード内に存在する場合)
削除したいキーが葉ノードに存在するとき、そのままキーを削除します。
削除後に葉ノード内のキー数がt - 1以上の場合は、これで終了です。t - 1を下回る場合は、兄弟ノードからのキー移植やノードの結合を行うことでB-Treeの条件を満たすように更新していきます。
t - 1以上の場合
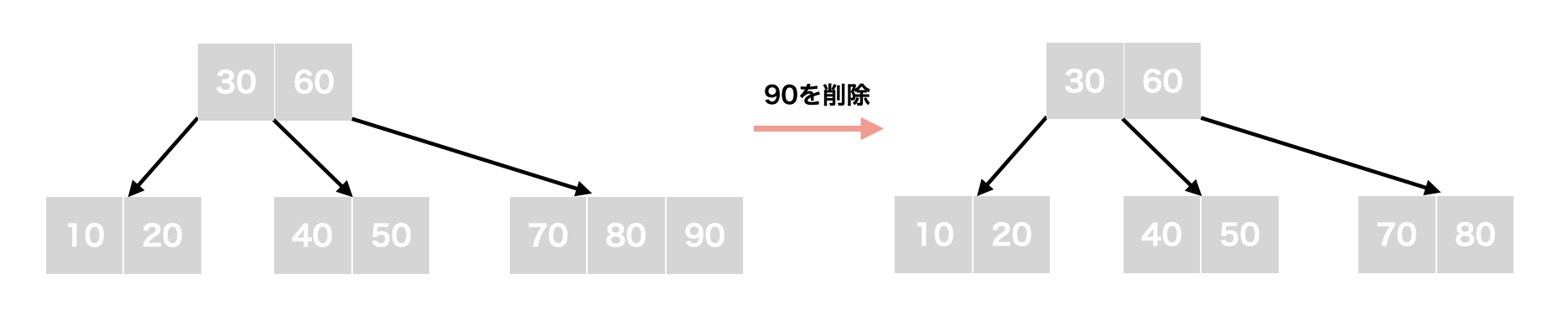
先ほどのB-Treeにてキー:90を削除する場合、そのまま90を削除します。削除後、対象ノード内のキー数は2であり、t - 1以上であるため、これで削除が完了です。
t - 1未満の場合(アンダーフロー)
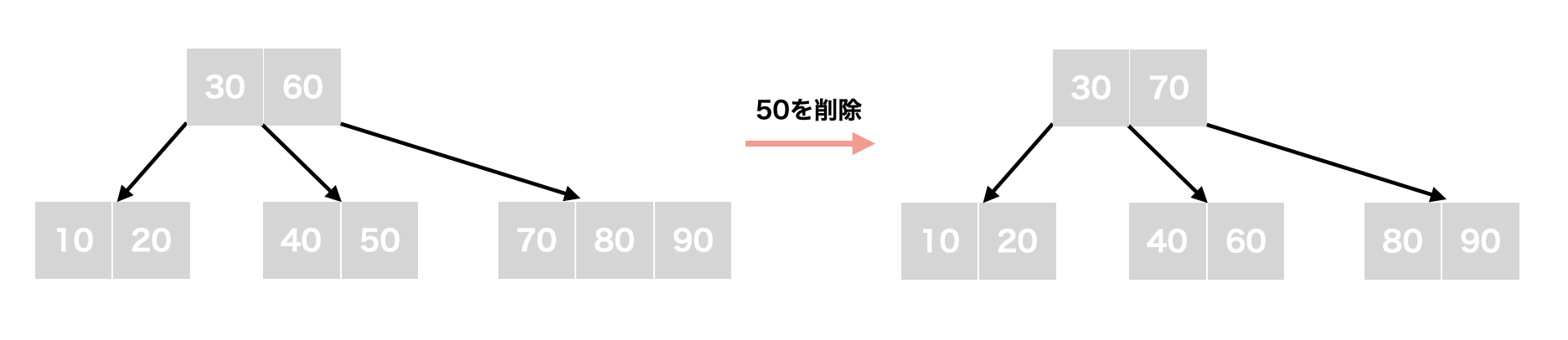
キー:50を削除する場合も同様に、まず50を削除します。この時、対象ノードのキー数は1となりt - 1を下回るため、兄弟ノードからキーを移植することで、B-Treeの条件を満たすようになります。
削除 (対象キーが内部ノードに存在する場合)
内部ノード内のキーを削除する場合は、対象ノードの左の子ノードの最大値、または右の子ノードの最小値を内部ノードに持ってくることで削除後もB-Treeの条件を満たすようになります。
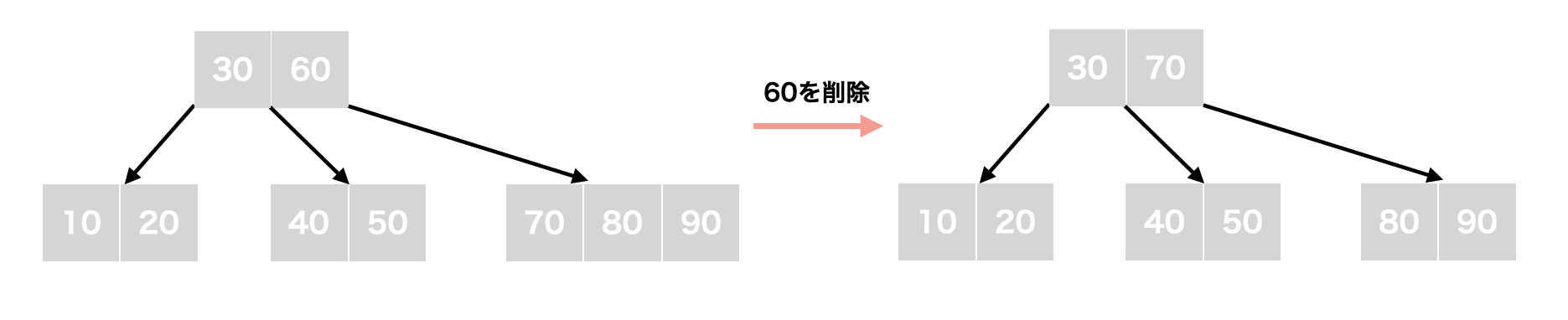
内部ノード(根ノード)のキー:60を削除する場合を考えます。60を削除して、根ノードの右の子の最小値である70を根ノードに移植してきます。
B-Treeの時間計算量
挿入・削除の例で見たように、B-Treeはそれぞれのノードが保持する最大・最小ノード数の条件を守りながら更新を行なっていくため、木のバランスが保たれます。これにより、検索、挿入、削除などの操作をO(logN) の時間計算量で行うことができます。(N:レコード数)
B-Treeはキー値の比較を行い子ノードに進んでいく中で、毎回探索範囲を1 / 子ノード数だけ減らしていきす。これにより全てのレコードを調べる必要がないため、パフォーマンスが向上します。
B-Treeインデックスをいつ使用するべきか
大規模なテーブルに作成
データ量が少ないテーブルの場合、フルスキャンとB-Treeインデックスの処理速度に大きな差はありません。そのため、レコード数の少ないテーブル内のカラムにインデックスを作成しても効果はありません。レコード数が1万行以下の場合は、ほとんど効果がないようです。
カーディナリティの高い列に作成
カーディナリティとは、あるテーブルのカラムが持つデータの種類の数です。
ここで、「性別」と「メールアドレス」の例を考えてみます。性別カラム内のデータは、「男性」、「女性」、「不明」の3種類になり、カーディナリティは3となり低いです。一方で、メールアドレスは重複が許されないためユーザーの数だけメールアドレスが存在することになります。よって、メールアドレスカラムのカーディナリティは高いです。
カーディナリティの高い列に作成する理由
まず、カーディナリティが低いカラムにインデックスを作成する場合を考えます。ここでは便宜上、「男性:1」、「女性:2」というデータを50%ずつ持つ性別カラムを考えます。
この場合、かなり大雑把に捉えると、B-Treeの左の部分木には1、右の部分木には2が配置されます。よって、キー: 1を探索する場合、B-Treeの左の部分木、つまり半分のデータを探索する必要があり、B-Treeの良さを活かすことができません。
逆に、メールアドレスのような重複がないカラムにB-Treeインデックスを作成すると、毎回の探索で探索範囲が減っていくので、高速に探索を行うことができます。
SQL文の条件に使用される列
インデックスは検索などの処理を高速化するために使用されます。それにもかかわらず、クエリの検索条件として使用されない列にインデックスを貼っても、全く意味がありません。SQLの検索条件や結合条件に使用される列にインデックスを作成することで、インデックス使用のメリットが得られます。
B-Treeインデックスの作成方法
以下がMySQLでB-Treeインデックスを作成するためのSQL文になります。
CREATE INDEX インデックス名 ON テーブル名 (カラム名1, カラム名2, ...);
B-Treeインデックスのメリット
これまで見てきたように、B-Treeは検索、挿入、削除などの処理を比較的高速に行うことができます。また、B-Treeはキーを昇順にソートして保持するため、等号(=)を使用した検索だけでなく、BETWEENや、不等号(<、>)を使用した範囲検索に対しても高速に動作します。
B-Treeインデックスの注意点
挿入・削除を繰り返すと非平衡木になる
B-Treeは、挿入・削除が行われる際に、B-Treeの条件を満たすようにノードの分割・結合を行うことで自動的にバランスを保ちます。しかし、挿入や削除などの処理が繰り返し行われることで、非平衡木になってしまうことがあります。そうすると、パフォーマンスが劣化してしまうので、インデックスの再構築が必要になります。
更新性能が劣化する
インデックスが作成されているカラムのデータを変更すると、B-Treeで保持しているデータも変更する必要があります。具体的には、B-Tree内の変更前のデータを削除し、変更後のデータを挿入する必要があります。これにより、テーブルにインデックスを作成すればするほど、そのテーブルへの更新処理が重くなってしまいます。
インデックス作成による検索・挿入・削除の高速化と、更新速度劣化のトレードオフを意識して、インデックスを作成する必要があります。
主キーなどの一意制約の列には作成不要
主キーや一意制約のカラムに対して、DBMSは自動的にB-Treeインデックスを作成しているため、重複してインデックスを作成する必要はありません。
SQL文の否定条件には効果がない
SQLクエリで!=, <>などの否定条件を使用すると、指定した値以外の全ての値を調べる必要があるため、B-Treeインデックスを効果的に利用することができません。
参考
Organization and maintenance of large ordered indexes (R. Bayer, E. M. McCreight)
Organization and maintenance of large ordered indexes(PDF)
達人に学ぶDB設計徹底指南書 初級者で終わりたくないあなたへ(ミック)
Understanding B-Tree (Medium)
B-Tree Indexing Basics Explained (Medium)
Database Indexing with B-Tree & B+Tree (Medium)
Introduction of B-Tree (GeeksforGeeks)
Insert Operation in B-Tree (GeeksforGeeks)
B Tree Insertion (JavaTpoint)
Deletion from a B-tree (Pragramiz)
Deletion In B-Tree In C (PrepInsta)
Primary Indexing in Databases (GeeksforGeeks)
Indexing in DBMS (JavaTpoint)
B-Trees (UT Austin)
B-Trees (Cornell Computer Science Department)
インデックスの役割と構成 (Qiita)