最もシンプルな環境の強化学習を書いてみた

概要

　最も単純な環境で強化学習を構築してみます．2次元のランダムウォークを参考にして，上下左右に動く点粒子をエージェントと設定します．

　今回は離散型の強化学習を前提にしているため，上下左右の同じ加速度から一つを毎ループ選択するような形にします．
　xyどちらかが-1.0～1.0をはみ出したら終了し，その範囲の正方形の下の辺に当たったら報酬を1与えるとします．他は全部報酬0です．

準備

　python = "3.6.8"
　pytorch = "1.6.0"

コード

　・エージェント（自身の位置を知覚できない設定）

agent.py

import random
import numpy as np

import torch
import torch.nn as nn
import torch.nn.functional as F

class Agent(nn.Module):
    def __init__(self,device):
        super(Agent,self).__init__()
        self.action_space = [np.array([0.1 ,0.  ]),  #取れる行動は4つ
                             np.array([0.  ,0.1 ]),
                             np.array([-0.1,0.  ]),
                             np.array([0.  ,-0.1])]

        self.v = np.random.randn(2)*0.1 #初速度は正規分布
        self.a = random.choice(self.action_space) #初加速度は一様分布で選択
        
        #方策の確率モデル 2層のNN
        self.neural = nn.Sequential(nn.Linear(2,100), nn.Sigmoid(), nn.Linear(100,4))
        self.device = device
    
    #エージェントの状態リセット
    def reset(self):
        self.v = np.random.randn(2)*0.1
        self.a = random.choice(self.action_space)
    
    #方策からサンプリングで状態（速度）から行動選択(0~3)を返す．30%の確率で完全ランダム
    def act(self):
        if random.random()<0.7:
            with torch.no_grad():
                act_probs = F.softmax(self.neural(torch.tensor(self.v).float().to(self.device)))
            act_index = torch.multinomial(act_probs, num_samples=1).item()
            self.a = self.action_space[act_index]
        else:
            act_index = random.choice([0,1,2,3])
            self.a = self.action_space[act_index]
        return act_index
    
    #方策に従って状態（速度）から次の行動選択(0~3)を返す
    def determine_act(self):
        with torch.no_grad():
            act_probs = F.softmax(self.neural(torch.tensor(self.v).float().to(self.device)))
        act_index = torch.argmax(act_probs).item()
        self.a = self.action_space[act_index]
        return act_index

    #ステップ
    def step(self):
        self.v += self.a
    
    #速度を引数に次の行動選択の確率を返す
    def forward(self, v):
        act_probs = F.softmax(self.neural(torch.tensor(v).float().to(self.device)))
        return act_probs

　・環境

env.py

import numpy as np

class Environment():
    def __init__(self):
        self.agent_pos = np.zeros(2) #環境内にいるエージェントの座標

    #環境リセット
    def reset(self):
        self.agent_pos = np.zeros(2)
    
    #ステップ
    def step(self, agent):
        self.agent_pos += agent.v

        if np.any(np.abs(self.agent_pos)>1.0) and self.agent_pos[1]<-1.0:  #下の辺に接触
            reward = 1
            complete = True
        elif np.any(np.abs(self.agent_pos)>1.0):  #正方形の範囲から飛び出す
            reward = 0
            complete = True
        else:  #正方形の範囲内
            reward = 0
            complete = False
        
        return self.agent_pos, reward, complete

　・報酬から価値を計算します
　・注目する行動から，エピソードの最後まで割引報酬和を取ります．

main.py

def reward_to_value(story):
    act_value = []
    for i, s in enumerate(story):
        gamma_rate = 0.99
        gamma=1.0
        value = 0.0
        act_index = s[0]
        for j in range(1,len(story)-i+1):
            value += story[i+j-1][2]*gamma
            gamma *= gamma_rate
        act_value.append((act_index,s[1],value))
    return act_value

　・PolicyGradientの考え方から損失関数を書きます

\nabla _{\theta }J\left( \theta \right) =E\left[ \nabla _{\theta }\log \pi _{\theta }\left( s,a\right) Q^{\pi_{ \theta} }\left( s,a\right) \right]

　・サンプル用に期待値Eを外して，PyTorchのパラメータ更新に合わせてマイナスを付けます

pgloss.py

import torch
import torch.nn as nn
import torch.nn.functional as F

class PGLoss(nn.Module):
    def __init__(self):
        super(PGLoss, self).__init__()
    
    def forward(self, acts, preds, values):
        acts_one_hot = F.one_hot(acts, num_classes=4).to(preds.device)
        loss = -(torch.log(preds)*acts_one_hot).sum(-1)*values
        return loss.mean()

　・サンプリングを含む学習ループを書きます．

main.py

from agent import Agent
from env import Environment
from pgloss import PGLoss

from tqdm import tqdm
from copy import deepcopy
import pickle
import numpy as np
import matplotlib.pyplot as plt

import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
from torch.utils.data import DataLoader
import torch.optim as optim

agent = Agent(device).to(device)
optimizer = optim.SGD(agent.parameters(), lr=0.001)
env = Environment()
pgloss = PGLoss().to(device)

def reward_to_value(episode):
    act_value = []
    for i, s in enumerate(episode):
        gamma_rate = 0.99
        gamma=1.0
        value = 0.0
        act_index = s[0]
        for j in range(1,len(episode)-i+1):
            value += episode[i+j-1][2]*gamma
            gamma *=gamma_rate
        act_value.append((act_index, s[1], value))
    return act_value

for epoch in range(1000):  #1000エポック学習
    #1Epoch
    pos_historys = []
    
    #Test roop
    for j in range(100):  #100サンプルでテスト
        agent.reset()
        env.reset()
        pos_history = []
        for i in range(300):  #300stepで終わらなければ切る
            act_index = agent.determine_act()
            agent.step()
            agent_pos, reward, done = env.step(agent)
            pos_history.append(deepcopy(agent_pos))
            if done: break
        pos_historys.append(pos_history)
    
    #図を保存
    plt.figure()
    plt.xlim(-1.0,1.0)
    plt.ylim(-1.0,1.0)
    for pos_history in pos_historys:
        pos_history = np.array([np.zeros(2)]+pos_history)
        plt.plot(pos_history[:,0],pos_history[:,1])
    plt.savefig("./img/epoch"+str(epoch)+".png")
    
    #Sample roop
    samples = []
    for j in range(500):  #100サンプルでテスト
        #1Sample
        agent.reset()
        env.reset()
        episode = []
        for i in (range(300)):  #300stepで終わらなければ強制終了
            act_index = agent.act()
            agent_v = deepcopy(agent.v)
            agent.step()
            agent_pos, reward, done = env.step(agent)

            episode.append((deepcopy(act_index), deepcopy(agent_v), deepcopy(reward)))
            if done: break

        samples += reward_to_value(episode)  #500エピソード分の行動とエージェントの状態と

    dataloader = DataLoader(samples, batch_size=200, shuffle=True)
    for batch in dataloader:
        act_index, agent_v, value = batch
        act_index = act_index.to(device)  #サンプリングされた行動
        agent_v = agent_v.to(device)  #サンプリングされた速度
        value = value.to(device)  #行動価値

        optimizer.zero_grad()
        act_probs = agent(agent_v)  #状態（速度）から各行動の確率
        loss = pgloss(act_index, act_probs, value)  #行動の確率，価値，実際の行動から損失を計算
        loss.backward()
        optimizer.step()

結果

　・1Epoch学習した後

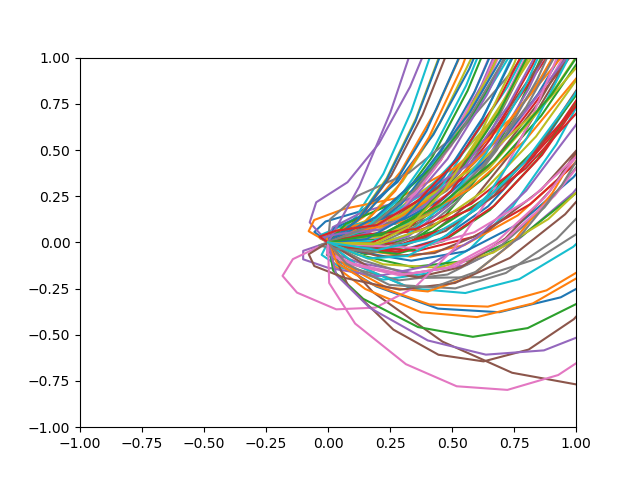
　・2Epoch学習した後

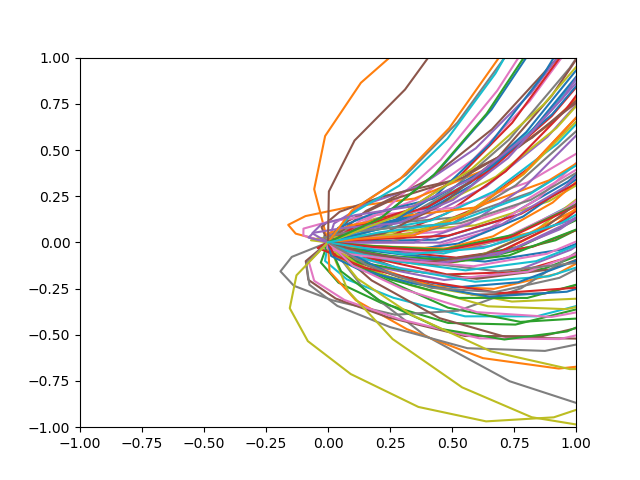
　・15Epoch学習した後

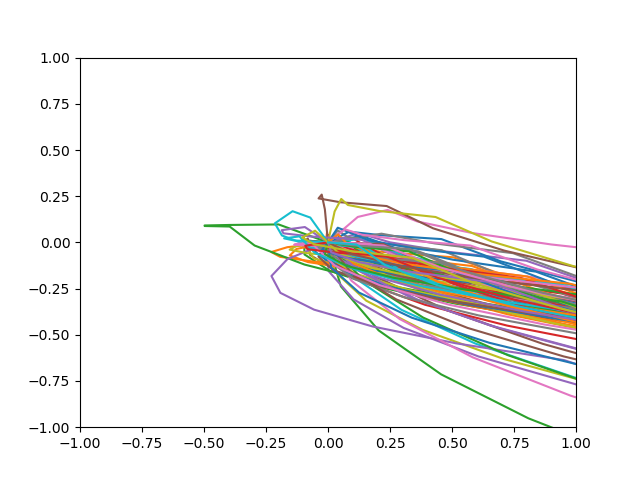
　・20Epoch学習した後

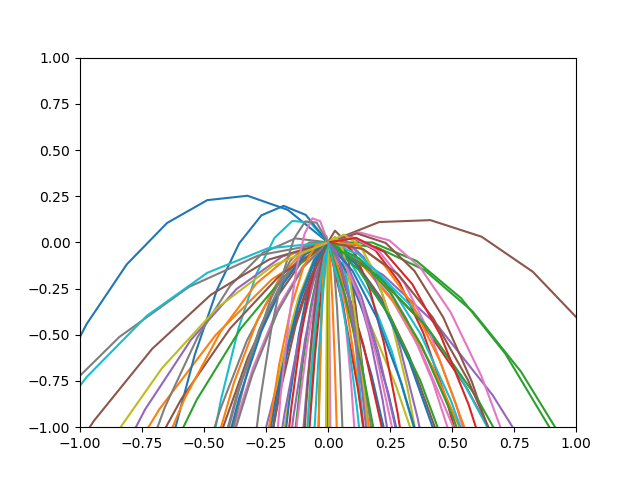
　・50Epoch学習した後

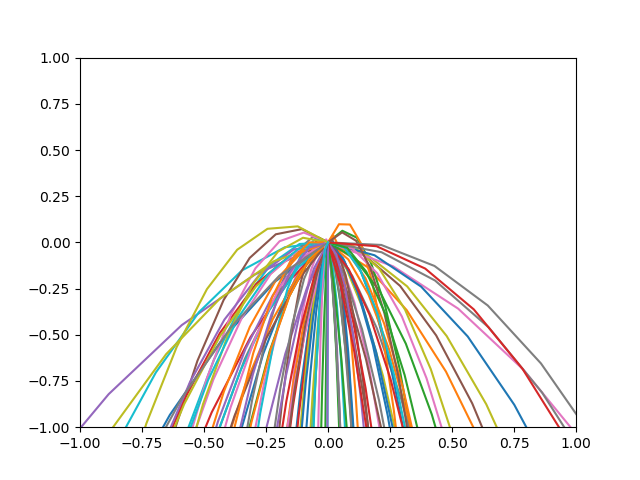
　・100Epoch学習した後

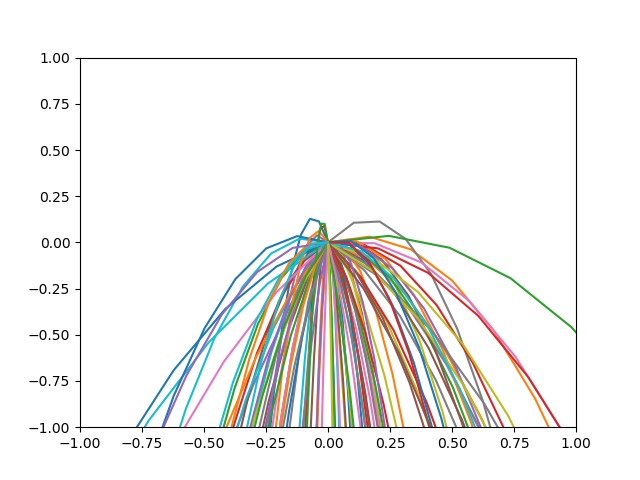
　・きちんと範囲の正方形の下の辺に向かうように学習されました．
#まとめ
　・超シンプルな環境でモンテカルロ法ベースの強化学習を行いました．
　・PGのひな形のつもりで書きましたが，ソースコードが長くなってしまい反省しております．

最後に

　・誤っている部分等ございましたら，コメント等で優しく指摘して頂けると嬉しいです．（気付かなかったら申し訳ありません）