挨拶
はじめまして、東京大学物理学科三年の佐々木保昂と申します。最近、朝起きてコーヒーを飲んでから一日をスタートしています(弊学科の小形先生のHP[A])。心なしか、集中力が上がっている気がするのでおすすめです。
さて、今回は統計物理学班の副班長として、
(1)統計物理班とは
(2)Physics Lab.の活動
(3)今年のノーベル物理学賞と統計力学の関連
の3つについて紹介しようと思います。
この記事で説明すること
-
統計物理学とは
Physics Lab.の統計物理班では、統計物理学を学んでいます。ここでは統計物理学について軽く紹介します。 -
Physics Lab.の活動
自主ゼミで扱っている本と五月祭企画について紹介します。 -
2024年度ノーベル物理学賞と統計物理学の関係
踏み込んだ話題として、2024年度ノーベル物理学賞のテーマでもあるHopfield modelを例に、その背景には統計物理のIsing modelと関連があることを解説します。
統計物理学とは
統計物理学班では、物質の巨視的な性質を微視的な法則から説明・解明する統計物理学という分野について学んでいます。身の回りの物質はアボガドロ数オーダーの原子から構成されており、巨視的には比熱や磁性、電気伝導性などの様々なふるまいを物質ごとに示します。それらの個々の粒子は運動方程式やシュレディンガー方程式などのミクロな法則に従っていると考えられるわけですが、
(1)その方程式は非線形になることがある
(2)解かなければいけない方程式の数が膨大である
ことから、ミクロな法則のみから物質の巨視的な性質を導くのはとても難しい問題となります。また、その巨視的な性質とミクロな法則とを直感的に結び付けることも簡単なことではないですね。
そこで、統計物理ではこのような多体系でみられるミクロなふるまいとは質的に違うマクロなふるまいを理解するために、確率論の導入や系の持つ対称性の破れなどに着目して、マクロな物理量の値を考えたり、秩序変数のふるまいから相転移を考えたりしてミクロな法則とマクロな性質を結びつけます。詳細な分野の違いについては、前年度記事[B]を参考にしてください。
Physics Lab.の活動
ここでは、統計物理班が(1)自主ゼミで扱っている本と、(2)五月祭企画について簡単に紹介します。
自主ゼミで扱っている本
- 『統計力学Ⅰ/Ⅱ』田崎晴明 著
統計力学の入門書です。量子統計から入っており、エルゴート性に関する議論を考えずに入れることがとてもありがたいです。B2で毎年3つぐらいゼミが立っています。 - 『ファインマン統計力学』 R.P.ファインマン 著 西川 恭治 監訳
自分は読んでいませんが、B2の方々が読んでいます。解析力学を微分幾何を使って考えているようで難しそうです。 - 『統計力学の基礎Ⅰ』清水明 著
今年発売された本です。私は熱力学の基礎は持っており、よく参考にしています。駒場時代の授業を踏まえて作成していると思いますが、N次元球の表面積に関するロールケーキとまんじゅうの例えがもしかしたら書いてあるかもしれません。 - 『物性物理のための 場の理論・グリーン関数』小形正男 著
弊学科の小形先生の本です。ダイヤグラムによって線形応答理論の具体的な計算ができることが一つの目標となります。 - 『固体電子の量子論』浅野健一 著
私が参加しています。まじめに読んだら2年ぐらいかかりそうです。数式と物理的な説明が少し飛躍していると感じるため、そこを埋めることが勉強になっています。 - 『Field Theories of Condensed Matter Physics』 Eduardo Fradkin 著
(統括による評)トポロジカルな物性を中心に、場の理論を用いて凝縮系物理を扱う教科書です。必要とする数学や道具の説明にページが割かれており、また豊富なトピックを扱っているのが良い点だと思いますが、記述が曖昧な箇所も多いため、他の本を (たくさん) 参照しながら読み進める必要がありそうです
五月祭企画
五月祭では、統計物理班はトポロジーをテーマとして、それに関わる統計物理の演示実験や東大の研究室で行った実験の成果発表を予定しております。現在準備中ですが実空間、波数空間でのトポロジーや、生物におけるトポロジーの役割など様々なテーマに触れようと思っているので、ぜひ、おこしください。
2024年度ノーベル物理学賞と統計物理学の関係
次に踏み込んだ話題として、この話題を書くなら今年かなぁと思い、今年のノーベル物理学賞と統計力学の関連について紹介しようと思います。2024年度のNobel物理学賞は、Hopfield, Hintonが受賞しました。彼らは、現在のニューラルネットワークによる機械学習に基礎的貢献をしたことで受賞していますが、その考えの源流に統計物理学が関わっているのはご存じでしょうか?Nobel賞 公式サイトのアンケート[C]によると、半数の方が知らないようなので軽く触れておきたいと思います。
まず、統計力学において、Ising modelは統計物理学において磁性体のふるまいを確認できる簡易的な模型です。1924年あたりにIsingが提案したようなのでちょうど100周年になるらしいです[D]。1,2次元の場合には、厳密解が知られており、統計力学の入門的モデルとして広く学ばれています。下の図1に1次元Ising modelのセットアップを述べます。N個のスピンが1次元上に並んでいるときのIsing modelのハミルトニアン(エネルギー)は以下のようになります。
\begin{align}
H=-J\sum_{\langle i,j \rangle} S_i S_j -h\sum_{i=1}^{N} S_i
\end{align}
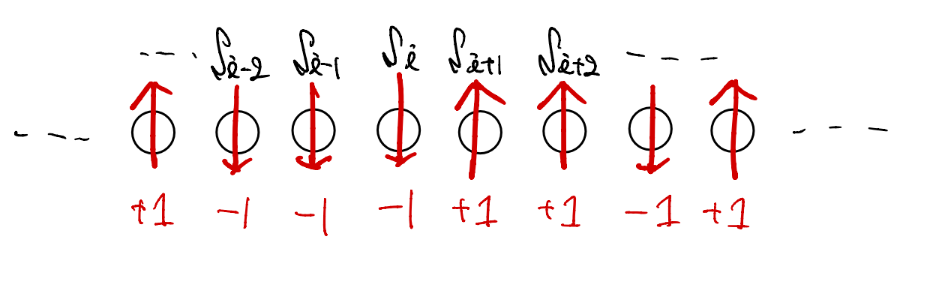
図1 Ising modelの概要図。 赤い矢印の上下がスピン$S$が$\pm 1$をとることを表す。
ただし、$S=\pm 1$であり、$\langle i,j \rangle$は隣接しているスピンについて和を取ることを表しています。このモデルは、2次元以上の場合に有限温度で相転移が起きてスピンが揃う秩序相があるということが確認されています1。
次に、Hopfield modelについてです。Hopfieldモデルは、物理学におけるIsingモデルの概念を基に人工知能の分野で発展したニューラルネットワークモデルです。特定のスピン状態を記憶として保存し、記憶をパターンとして再現する機能を持っています。このモデルのハミルトニアン(エネルギー関数)は以下のようになります。
\begin{align}
H=-\frac{1}{2}\sum_{i,j}w_{ij}x_ix_j-\sum_{i=1}^N \theta_i x_i
\end{align}
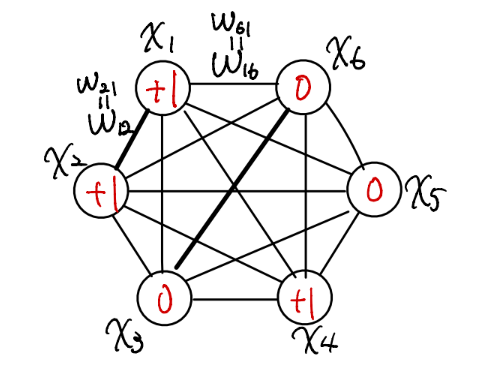
図2 Hopfield modelの概要図。 $x_i=0,1$はニューロン$i$が発火しているかどうかを表す。
Hopfield modelでは、$N$個の$x=0,1$である二値ノードを持つネットワークを考えます。$x$は各ニューロンの発火を示し、$\theta$はバイアス、$w_{ij}=w_{ji}$は$i,j$のニューロン間の相関の強さを反映します。そして、行ベクトル$(x_1,\cdots x_n)$の特定の組がひとつの記憶を表していると考えます。
ここでは、$s=1,2,\cdots,Q$として$Q$個の記憶の組$(x_1^s,\cdots x_n^s)$を知っているとしましょう。このとき、$w_{ij}$は$w_{ij}=\frac{1}{Q}\sum_{s=1}^{Q}(2x_i-1) (2x_j-1)$で与えられます。2
そのもとで
\begin{align}
u_i(t)=\sum_{j=1}^{N}w_{ij}x_j(t)+\theta_i (t)
\end{align}
\begin{equation}
x_i(t+1) =
\begin{cases}
1 & (u_i(t) > 0) \\
x_i(t) & (u_i(t)=0)\\
0 & (u_i(t) < 0)
\end{cases}
\end{equation}
のように$x(t)$をランダムに選びながら更新していきます。すると、エネルギー関数$H$は更新ごとに単調減少することが知られており、$H$が極小値になった時、最初に記憶した$x_i$の組が(理想的には)実現されます3。このことから、Hopfield modelは連想記憶のモデルとして知られています。
さて、Ising modelのハミルトニアン$H$を$J\rightarrow w_{ij}, \ S\rightarrow x, \ h\rightarrow\theta_i$という風に変更するとHopfield modelの$H$になっているかと思います。1次元IsingモデルとHopfieldモデルは、ハミルトニアンとエネルギー関数の形が似ていて、エネルギーを最小にする仕組みを用いています45。
このように一見単純な物理モデルが、人工知能といった全く異なる分野での応用可能性を持っていることは非常に面白いと思います。Hopfield modelは、機械学習の発展の源が統計力学に以前からあったIsing modelと関連しているという例ですが、最近では機械学習の知見を統計力学に持ち込もうという流れも注目を集めています6。
さいごに
最後になりますが、この記事をきっかけにPhysics Lab.や統計物理学により関心を抱いていただけると幸いです。