3次元動作データをPythonで可視化してみた

モーションキャプチャで取得した3次元のマーカー座標データから膝の角度変化をPythonで可視化してみました。

使用データ

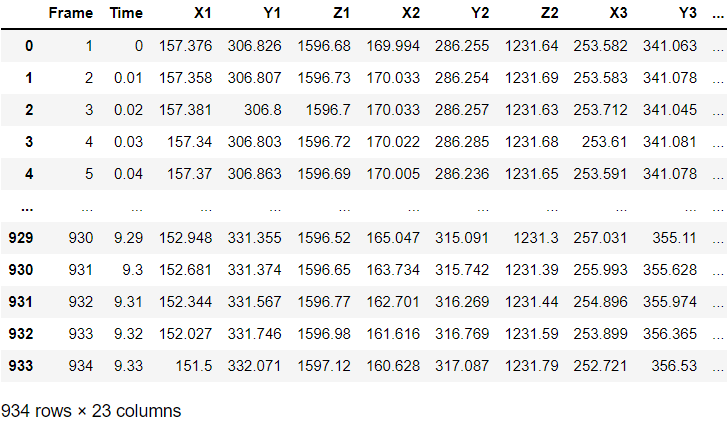
膝の周り7か所に貼ったマーカーから取得した座標データ

計算方法

beta_knee_angle = []
alpha_knee_angle = []
gamma_knee_angle = []

for i in range(934):
    G_T = np.array(df_knee.loc[1+i,['X1','Y1','Z1']].astype(float).values.tolist())
    L_EC = np.array(df_knee.loc[1+i,['X2','Y2','Z2']].astype(float).values.tolist()) 
    M_EC = np.array(df_knee.loc[1+i,['X3','Y3','Z3']].astype(float).values.tolist()) 
    L_C = np.array(df_knee.loc[1+i,['X4','Y4','Z4']].astype(float).values.tolist()) 
    M_C = np.array(df_knee.loc[1+i,['X5','Y5','Z5']].astype(float).values.tolist()) 
    L_M = np.array(df_knee.loc[1+i,['X6','Y6','Z6']].astype(float).values.tolist()) 
    M_M = np.array(df_knee.loc[1+i,['X7','Y7','Z7']].astype(float).values.tolist()) 
    
    #G_T,L_EC,M_ECから太もものローカル座標をつくる
    #ローカル座標：p
    #L_ECとM_ECの中点をN_ECとする
    N_EC = (L_EC+M_EC)/2
    
    k_p = (G_T-N_EC)/np.linalg.norm(G_T-N_EC)
    i_tmp = (L_EC-N_EC)/np.linalg.norm(L_EC-N_EC)
    j_p = np.cross(k_p,i_tmp) #外積
    i_p = np.cross(j_p,k_p)
    
    
    #L_C,M_C,L_M,M_Mから太もものローカル座標をつくる
    #ローカル座標：d
    #L_CとM_Cの中点をN_Cとする
    #L_MとM_Mの中点をN_Mとする
    N_C = (L_C+M_C)/2
    N_M = (L_M+M_M)/2

    k_d = (N_C-N_M)/np.linalg.norm(N_C-N_M)
    i_tmp = (L_M-N_M)/np.linalg.norm(L_M-N_M)
    j_d = np.cross(k_d,i_tmp) #外積
    i_d = np.cross(j_d,k_d)
    
    
    # β角：外転内転
    # α角：屈曲伸展
    # γ角：内旋外旋

    # β角の結果を他の2方向の角度計算に利用する
    beta = np.arcsin(np.dot(k_d,i_p))
    beta_angle = np.rad2deg(beta) 
    beta_knee_angle.append(beta_angle)
        
    alpha = np.arccos(np.dot(k_d,k_p)/np.cos(beta))
    alpha_angle = np.rad2deg(alpha) 
    alpha_knee_angle.append(alpha_angle)
   
    gamma = np.arccos(np.dot(i_d,i_p)/np.cos(beta))
    gamma_angle = np.rad2deg(gamma) 
    gamma_knee_angle.append(gamma_angle)

各軸ごとの角度を可視化

matplotlibで3軸それぞれの時系列角度変化を可視化してみた。
plt.plot(time, 角度を格納したリスト)で3軸についてやってみる。

# α角：屈曲伸展
fig = plt.figure()

plt.plot(time,alpha_knee_angle)
plt.xlim(time[0],time[-1])

xmin, xmax = time[0],time[-1]
plt.hlines(0, xmin, xmax,colors='gray',linestyle='dashed')

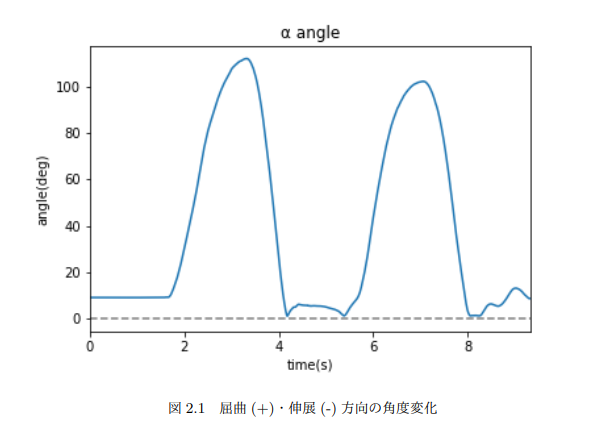
plt.title("α angle")
plt.xlabel("time(s)")
plt.ylabel("angle(deg)")

今回のデータでは膝が2回屈曲していたことがグラフからもよく分かる。

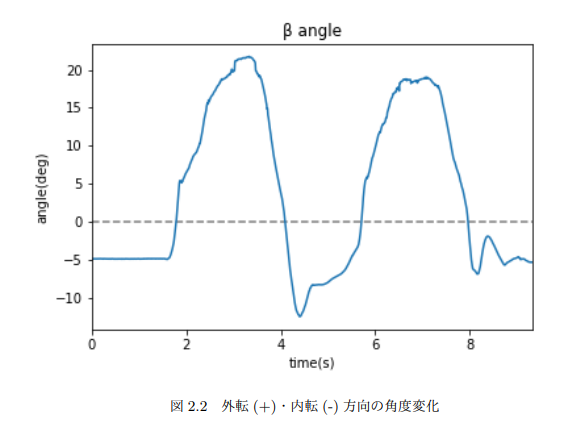
外転内転方向の動きも2つの山があり、屈曲動作と連動してるなーと分かる。ただ変化角度はα角と比べると小さい。

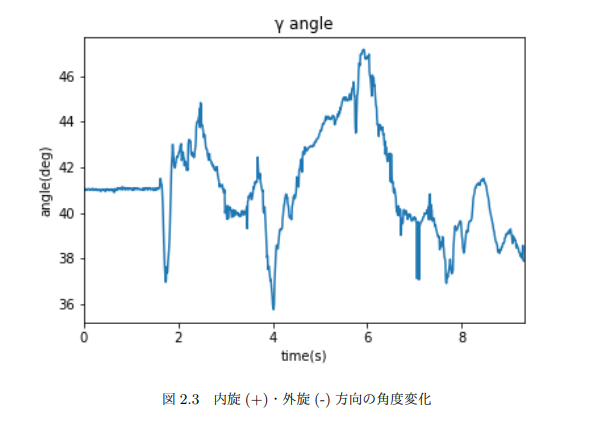
上2つのグラフと違って2つの大きな山があるわけではないので、この軸方向の動きは膝の屈曲動作ではあまり動かさない方向だと分かる。
変化角度も±10もないくらいなので目で見てもあまり分からない変化だろうなーと想像できる。