はじめに
この記事はFOA based DMDに関するノート(アルゴリズム編)の続きである。
今回は前回紹介したアルゴリズムをJuliaで実装する。「とりあえず動けばいい」レベルの簡単なコードだが、これはJulia初心者だから...ではなく、単に当方のスキル不足が原因なのでご寛恕いただきたい。
なお、Juliaのバージョンは1.3である。
SVD based DMD
まずは比較用としてSVD based DMDを実装する。このアルゴリズムについては前回の記事で紹介したこの文献などで解説されている。入力はデータ行列と打ち切り特異値分解のターゲットランクである。また、キーワードオプションで高次元モードの計算方法を切り替えられるようにしている(いわゆるExact/Projected DMDの違い)。
Python同様、疑似コードをそのまま書けばいいのがJuliaの嬉しいところ。
function SVD_based_DMD(D,r;opt="exact")
X = D[:,1:end-1]
Y = D[:,2:end]
U, S, V = svd(X)
U = U[:,1:r]
iSr = Diagonal(1.0./S[1:r])
V = V[:,1:r]
Atil = U' * Y * V * iSr
mu, W = eigen(Atil, sortby=x->abs(imag(x)))
if opt == "projected"
Phi = U * W # Projected DMD
else
Phi = Y * V * iSr * W # Exact DMD
end
return mu, Phi
end
個人的に引っかかった点としてはiSr = Diagonal(1.0./S[1:r])だ。除算のスラッシュの前にピリオドをつけないと演算がbroadcastされないのだが、つけ忘れた場合でも結果がスカラーになり、計算自体はできてしまうので、最初はコードが間違っていることに気づかなかった(変な固有値が出てきて焦った)。Python(NumPy)だとその辺はあまり気をつけなくてもよかったので、注意が必要そうだ。
また、eigenのsortbyオプションに1変数の無名関数を渡すとそれを基準に固有値と対応する固有ベクトルをソートしてくれる。今回はモードを周波数の昇順でソートし、かつ複素共役の固有値を持つモードをペアとしてまとめたかったため、虚部の絶対値の大きさでソートしている。
FOA based DMD
こちらについても元論文の疑似コード通りに書けばよい。
function FOA_based_DMD(X,r)
n, m = size(X)
V = zeros(n,m)
H = zeros(m,m-1)
B = zeros(m,m)
s = zeros(m)
B[1,1] = norm(X[:,1])
V[:,1] = X[:,1] / B[1,1]
for j in 1 : m-1
B[1,j+1] = dot(H[1,1:j-1], B[1:j-1,j])
for i in 2 : j
B[i,j+1] = dot(H[i,i-1:j-1], B[i-1:j-1,j])
end
w = X[:,j+1]
for i in 1 : j
w -= B[i,j+1] * V[:,i]
end
w /= B[j,j]
H[1:j,j] = V[:,1:j]' * w
w = w - V[:,1:j] * H[1:j,j]
s[1:j] = V[:,1:j]' * w
H[1:j,j] += s[1:j]
w = w - V[:,1:j] * s[1:j]
H[j+1,j] = norm(w)
V[:,j+1] = w / H[j+1,j]
for i in 1 : j+1
B[i,j+1] += H[i,j] * B[j,j]
end
end
F = svd(B[1:m-1,1:m-1])
Atil = F.U[:,1:r]' * H[1:m-1,1:m-1] * F.U[:,1:r]
mu, W = eigen(Atil, sortby=x->abs(imag(x)))
Phi = V[:,1:m-1] * F.U[:,1:r] * W
return mu, Phi
end
なお、前回の記事では計算初期の処理はfor文の外に出さないとダメだといったが、Juliaの仕様では$j=1$のときdot(H[1,1:j-1], B[1:j-1,j])は0.0になるので、今回は元論文のアルゴリズム通りに実装している(この仕様に頼った書き方が果たしていいのか悪いのかという問題はあると思うけど)。
計算結果
テスト計算にはDMD関連のアルゴリズムの検証によく使われる2次元円柱周りの流れの渦度データ(この本を買うと付いてくる)を使用した。これはMATLABのmat形式のデータなのでMAT.jlを使えば簡単に読み込むことができる。
import MAT
vars = MAT.matread("../CYLINDER_ALL.mat")
D = vars["VORTALL"]
rank = 21
mu1, Phi1 = SVD_based_DMD(D,rank)
mu2, Phi2 = FOA_based_DMD(D,rank)
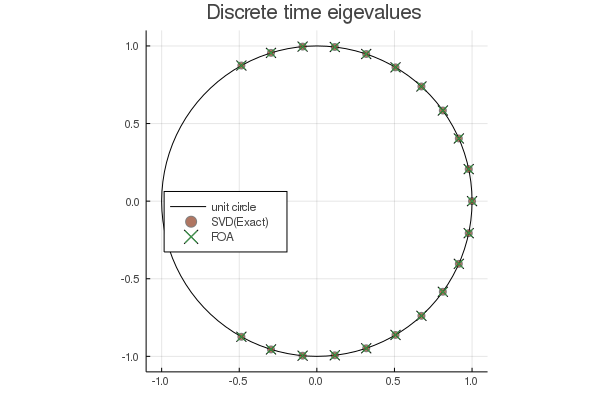
固有値分布を見ると、FOA based DMDの結果はSVD based DMDとよく一致している。

固有モードも見てみてると、やはり同様の結果が得られている(それぞれ複素モードの実部、絶対値、偏角)。ただし、分布に若干違いがある(固有ベクトルなので、両者で符号が反転していることは問題ではない)。これはExact DMDとProjected DMDで高次元モードの計算方法が異なるためだ。FOA based DMDはProjected DMDに分類される手法であるため、Exact DMDの結果と比較すると差異が現れるのである。

そこで、SVD based DMDの方もProjected DMDに変えたものと比較してみると上図のようになり、今度はモードの方もよく一致していることがわかる。というわけで、疑似コード通りの実装でも問題なく計算できることが確認できた。
余談だが、結果のグラフを書くときにPlots.jlを使ったのだが、2次元配列からコンターを書くときに軸の数値を他の変数(座標)に変更する方法がよくわからなったので、上の図では苦し紛れに軸そのものを消している(あと円柱がある部分に塗りつぶしの円を描く方法もわからなかった...)。matplotlibでできていたことを完全に再現することはまだ難しそうだ。おとなしくPyPlotを使えってことなんだろうけど。
まとめ
FOA based DMDをJuliaで実装し、計算がうまくいくことを確認した。今後はストリーミング形式のアルゴリズムなどもやってみようと思うが、個人的には直交基底をすべて保存しておくのはあまり好ましくないと思う。せっかく低ランク近似を適用するのなら、保存する直交基底の数もターゲットランクと同じオーダーに抑えたいところ。FOA based DMDでそれをやるかはともかく、そうした点を改善できればいいなと思う。