この投稿はFujitsu extended Advent Calendar 2016の17日目の記事です。
なお、記事は全て個人の見解です。会社・組織を代表するものではありません。
はじめに
Advent Calendarに投稿するのは初めて(そもそもQiita自体ほとんど使ったことない←)なのでコメントなんかはお手柔らかにオナシャス
今回は皆さんご存知の楕円曲線暗号についてご紹介したいと思います。また、ライブラリなどの使い方ではなく、暗号の数学的な理論をできるだけわかりやすくお伝えしたいと思います。
具体的な暗号方式の名前ではなく、楕円曲線を利用した暗号方式の総称です。なお、実際の暗号方式としては楕円ElGamal暗号などがあります。
今回は暗号方式の説明ではなく、楕円曲線自体の簡単な理論とイメージをお伝えしたいと思います。
理論
Wikipediaによりますと
暗号における楕円曲線とは、ある有限体$K$上の式$y^2=x^3+ax+b$を満たす全ての点$P=(x,y)$の集合に、無限遠点と呼ばれる特別な点$O$を加えたものである。ここで、$x$と$y$は有限体$K$の要素である。($K$の標数が2または3の場合、上式では不都合が生じるため、標数は2と3以外であるとする。)
・・・(゚д゚)ハァ?
群論を知らない人にとっては何を言っているかさっぱりだと思います。
そこで今からざっくり説明していこうと思います。
まず有限体とはその名の通り有限な体です。
※体は"からだ"ではなく"たい"と読みます。
簡単に言うとある値(ここでは標数)で割った余りの集合に対し、四則演算ができるようににしたものです。ちなみにこれを考えて何がうれしいのかというとコンピュータで正確に表せる有限の整数で任意の演算ができるということです。以降では具体的な例を挙げで説明します。
標数$p=11$の例を示します。
まず、11で割った余りを考えると{0,1,2,...,9,10}となります。
ここで足し算や掛け算は、計算したあと$p$で余りをとれば{0,1,2,...,9,10}の集合の一要素になることは簡単に想像できます。[例: $3\times5=15\equiv4$ (mod 11)]
引き算や割り算はどうなるのでしょう?
引き算の場合、計算結果がマイナスになる場合があります。マイナスの値は集合の一要素なのでしょうか?例えば、$-4$は{0,1,2,...,9,10}の集合の一要素なのでしょうか?
まず$-4$の定義は4と加算すると0になる数です。つまり、$4+(-4)=0$というのが$-4$の定義です。標数$p=11$のとき、$4+7=11\equiv0$ (mod 11)となるため$-4$は標数$p=11$のとき$7$ということになります。これでマイナスの数も{0,1,2,...,9,10}の集合の一要素になりました。
ちなみに$4^2=16\equiv5$ (mod 11), $(-4)^2=7^2=49\equiv5 $(mod 11)となり、通常の数学と同じく$4^2=(-4)^2$となります。(ちょっと美しい・・・)
続いて割り算です。割り算も引き算の時と同じように{0,1,2,...,9,10}の集合の一要素となるのでしょうか?
ここでは$\frac{1}{2}$を例にとって考えたいと思います。
もちろん$0.5$は{0,1,2,...,9,10}の集合の一要素ではありません。ではどのように考えたらいいのでしょうか?
今回も引き算の時と同じように定義に戻ってみましょう。
$\frac{1}{2}$の定義は$2$と乗算すると$1$になる数です。つまり、$2\times\frac{1}{2}=1$というのが$\frac{1}{2}$の定義です。標数$p=11$のときは、$2\times6=12\equiv1$ (mod 11)となります。よって標数$p=11$のとき$\frac{1}{2}$は$6$ということになります。ちなみに、$(\frac{1}{2})^2=\frac{1}{4}$になります。ぜひ確認してみてください。
※なお、標数が変われば$\frac{1}{2}$の値も変化します。[例: $p=13$のとき、$2\times7=14\equiv1$ (mod 13)より$\frac{1}{2}=7$となります。]
以上より、集合に対して(ちょっと工夫すれば)四則演算が成り立つということが分かったかと思います。
これでWikipediaの有限体と標数はマスターできたはずです←
ですので次は楕円曲線$y^2=x^3+ax+b$のイメージをつかみましょう。
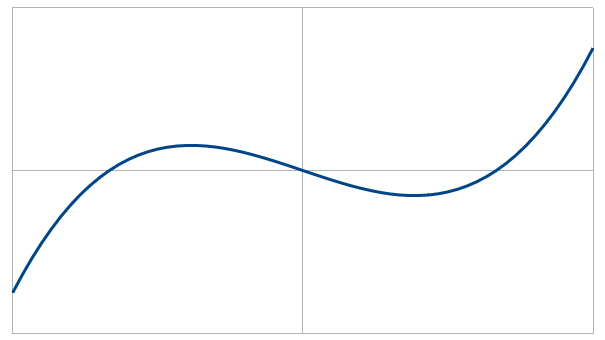
$y^2=x^3+ax+b$についてまず右辺を見ると3次曲線なのでこんな感じです。
左辺は$y^2$なのでマイナスの部分を切って(黄色の箇所)、正の部分を丸めて、+-の値があるので$x$軸対象のやつを加える(赤色の箇所)とこんな感じになります。
※ただし、楕円曲線上の変数(x,y,a,b)は有限体上の数なので0からp-1までの整数が点在しているようになります。(上のグラフはあくまでイメージです)
楕円曲線のイメージはできたと思いますので、次は楕円曲線上での演算(楕円加算)についてご説明します。
楕円曲線上の点P($x_p, y_p$)と点Q($x_q,y_q$)の加算は2点を通る直線と楕円曲線の交点の$x$軸対称の点と定義されています。グラフで表すと以下のようになります。

では点P($x_p, y_p$)と点Q($x_q,y_q$)を足した後の点R($x_r, y_r$)の座標はどうなるのでしょうか?
これに関しては私が改めて説明するまでもなく皆さんわかりますよね。2点を通る直線の公式は中学校の時に習ったはずですね。優秀な皆様なら私がいちいちこの説明をすることなんかうんざりするでしょう。
・・・ちなみに筆者はきれいさっぱり忘れてます。ゴ━━━━(# ゚Д゚)━━━━ルァ!!
正解は以下の通りです。
まず傾きを$\lambda$とすると$\lambda=\frac{y_q-y_p}{x_q-x_p}$です。傾き$\lambda$の直線と楕円曲線の交点の$x$軸対称の点R($x_r, y_r$)の座標は$x_r=\lambda^2-x_p-x_q$, $y_r=(x_p-x_r)\times\lambda-y_p$となります。(気力のある人は試してみてください。ちょっとひと工夫必要になります。)
いよいよ楕円曲線暗号のキモである楕円離散対数問題について説明します。
・・・楕円離散対数問題を紹介するのはめんどくさいので今回は本家の離散対数問題の具体例だけ紹介します。
Ω ΩΩ< な、なんだってー!!
a=2,n=5,p=11とします
またb=a^n mod p(a^nをpで割った余り)とします
つまりb=32 mod 11=10となります
離散対数問題とはaとbだけからnが何であるかを求める問題です
2を何乗すれば10になるかはぱっと見わかりませんよね
2^1,2^2,・・・と総当たりで計算するような方法しかないように思えます。
今回はn=5なのでコンピュータでやれば一瞬で求められますが、nをスパコンでも求められないように大きくしてやれば簡単には解けなくなります。
楕円離散対数問題はこれの楕円曲線版です。つまりn乗という掛け算の繰り返しだったところがn倍という楕円加算の繰り返しになるだけです。
この離散対数問題をベースにしたものを楕円曲線暗号と呼び、標数$p$が256-bitくらいだとスパコンなんかでも現実時間で解けないといわれています。(RSAの2048-bitより解きにくいといわれています。)
おわりに
今回は皆さんご存知の楕円曲線暗号について理論の雰囲気だけを説明しました。楕円曲線上での演算のイメージと離散対数問題がどんなのかということの雰囲気だけでもつかめていただければこの記事を投稿した甲斐があります。