More than 5 years have passed since last update.

交差再帰定量化解析（Cross Recurrence Quantification Analysis）ー理論編ー

Last updated at 2019-04-17Posted at 2019-04-16

概要

今回は発展的な時系列解析手法の１つである，交差再帰定量化解析を取り上げ，特にその理論を中心にまとめます．（勉強中なので間違ってたら指摘してください！）

交差再帰定量化解析とは

もともと，決定論に従う力学系の構造（決定論的カオス）を記述する手法．
二つの時系列データをもとに、それらがどれほど同じ繰り返しパターンで動いているのかを分析できる．
→ 近年，心理学やコミュニケーション実験の解析などにも用いられている．

比較すべき解析手法として，以下の手法を挙げておく．
統計量解析：データ全体にわたる強度，頻度，割合などを調べる時に有効
交差相関解析：データ間の共変動（=co-variation）ついて調べる時に有効
⇒変化が連動するタイミングが分かる
交差再帰定量化解析：データ間のイベントの再訪(=co-visitation)について調べる時に有効

必要な知識

・カオス解析とアトラクタ　アトラクタ構成－カオス解析解説－
相空間，アトラクタ，埋め込み，ターケンスの埋め込み定理についての理解（上記のサイトが非常にわかりやすい！）
・リカレンスプロット リカレンスプロット: 時系列の視覚化を越えて
リカレンスプロットに対してのおおざっぱなイメージ．（参考ＵＲＬの２ページ目くらいまでがなんとなくわかれば大丈夫）

##理論
大まかな流れとしては，

２つの時系列データそれぞれに対して，それを生成するアトラクタの再構成
交差再帰プロットの作成
各指標の算出
の手順で解析を進める．

１. アトラクタの再構成

時系列データがある動的システムから生成されたと考え，観測されるデータはシステムの状態（観測できないものも含む）によってのみ決定すると仮定する．
この時，システムの状態（運動）の軌跡（≈アトラクタ）を推定する．

具体的には，時系列データから，システムのすべての状態変数を復元する埋め込みを行う．
Ａ．時系列データX(t)を用意（t=0,1,2,...）
Ｂ．遅れ時間τを求める
遅れ時間は小さすぎると再構成された点が対角線のすぐ近くを動くことになり構造がほとんど潰れ，ノイズの影響を受けやすくなる．大きすぎると，バタフライ効果によって時間遅れ座標間の構造が消え去り，雑音特別できなくなる．
具体的には，時間遅れ相互情報量I(τ)が最初に極小となるτの値を用いる．(相互情報量)
時間遅れ相互情報量：

I(τ) = \sum_{x_{n}, x_{n-τ}} P(x_{n}, x_{n-τ})\log_2 \frac{P(x_{n}, x_{n-τ})}{P(x_{n}) P(x_{n-τ})}

ただし，

P(x_{n})：時刻nにx_{n}が起こる確率\\
P(x_{n}, x_{n-τ})：時刻nにx_{n}，時刻n-τにx_{n-τ}が起こる確率

言い換えると，X(t)とX(t+τ)の依存度が低くなるようなτを選択する．

Ｃ．埋め込み次元を求める
false nearest neighbor methodを用いる．
まずターキンスの定理より，ある有限の埋め込み次元 τ_0 で位相幾何学的性質を保ったアトラクタを再構成できることが知られている．

false nearest neighbor methodの直感的な理解としては，
１．時系列データX(t)から隣接するデータ点x(t),x(t+1)を取ってきて（とりあえず１次元と仮定，あとで拡張可），距離を計算する
２．埋め込みにより遅れ時間τを使って１次元増やす（結果的にデータ点x(t),x(t+1)も１次元拡張される）
３．再び距離を計算し，拡張前の距離と拡張後の距離を比較する
４．大きく変化していたら（急に隣接点が遠くに離れたら）位相幾何学的性質が保たれていないことになるため, １に戻りさらに埋め込みを行う
５．変化していなければ，拡張前の埋め込み次元が適切であるため決定する

これを数式で表すと，

R^2_{D}(t,r) = \sum_{k=0}^{D-1}[x(t+kτ)-x^{(r)}(t+kτ)]^2 \\
R^2_{D+1}(t,r) = R^2_{D}(t,r) + [x(t+Dτ)-x^{(r)}(t+Dτ)]^2 \\

に対して，

\frac{[x(t+Dτ)-x^{(r)}(t+Dτ)]^2}{R^2_{D}(t,r)} < R_{tolerant}

を満たさない点群ができるだけ少なくなる（e.g.全体の10%）最小のDを再帰的に求める.
ただし，

R^2_{D}(t,r)：D次元ベクトルx(t)と，D次元位相空間上でx(t)とr番目に近いデータ点の距離 \\
R^2_{D+1}(t,r)：D+1次元ベクトルx(t)と，D次元位相空間上でx(t)とr番目に近かったデータ点の距離
 R_{tolerant}：閾値（定数）

適切な埋め込み次元を求めることで，実際には近くない点が近くになってしまう事がないように拡張できる．決定すべきパラメータとして，半径(radius)がある．

２. 交差再帰プロットの作成

まず，位相空間内の軌跡が，十分に近い位置へ再び訪れた時，軌跡が再帰したと定義する．
Ａ．半径（radius）をいい感じに決定する（詳細は今度）
Ｂ．各次元の要素がX, Yそれぞれのデータの総数となるような２次元行列CR(x, y)を用意する．
Ｃ．各要素CR(i, j)に対して，D(i, j) < radiusならば1，そうでないなら0を代入.
これでクロスリカレンスプロットが完成！

例：サイン波（周期関数）のリカレンスプロット
（下図はクロスリカレンスプロットではないことに注意）

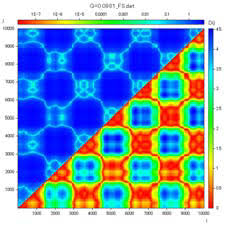
クロスリカレンスプロットの特徴

周期的な時系列データであれば周期的な空間パターンが現れ，そうでなければ非周期的なパターンが現れる
右上から左下にかけて対角線が現れれば，タイムラグ無しでイベントが共起していることを示す．
その対角線と並行な対角線が現れれば，その距離に応じたタイムラグでイベントが共起していることが分かる
定常的な時系列であれば，空間全体が一様になる
縦線や横線が現れている場合，その長さに応じて定常状態が継続していることを示す．

以上の特徴を抽出する指標について，さらに詳しくみていく．

３. 各指標の算出

CRPsから得られる指標として以下の代表的なものを取り上げる

再帰点の密度による指標

再帰率(RR)：
どのLagでCouplingが生じているかの度合いを調べるのに有効

RR = \frac{1}{N~2}\sum_{i,j=1}^{N} CR_{i,j} \\
CR_{i,j} = Θ(ε - |x_{i} - y_{j}|) \\
ε: プロットの閾値（=radius）

対角線による指標

リカレンスプロットの対角線をみる．まず，クロスリカレンスプロットから対角線の長さ**ヒストグラムP(l)**を作成する．その後，それを用いた指標について検討する．

P(l)=\sum_{i,j=1}^{N}(1-CR_{i-1,j-1})(1-CR_{i-l,j-l})\prod_{k=0}^{l-1}CR_{i+k,j+k} \\
(1-CR_{i-1,j-1})：長さｌ未満はカウントしない \\
(1-CR_{i+l,j+l})：長さｌ以上はカウントしない \\
\prod_{k=0}^{l-1}CR_{i+k,j+k}：(i,j)からはじまる長さLの間のすべての点がプロットされているならカウントする \\

決定率(DET)：
l_min以上の長さを持つ対角線を形成するリカレンスプロットの割合（＝孤立していないプロットの割合）を示す．
システムの将来の状態が事前の状態によって決定づけられるか（決定論的かどうか）の程度を表す．

　DET = \frac{\sum_{l=l_{min}}^{N}lP(l)}{\sum_{l=1}^{N}lP(l)}　\\
l_{min}：最低限の長さを決める閾値パラメータ．

最長な対角線の長さ：
指数関数的なカオスの発生を示す指標．

L_{max} = max(\{l_{i}\}_{i=1}^{N_{i}}) \\
N_{t} = \sum_{l>>l_{min}}P(l) \\
(=閾値以上の長さの対角線の本数の合計)

平均の対角線の長さ：
遷移の分岐＝システムの予測可能な時間の長さを示す．

L = \frac{\sum_{l=l_{min}}^{N}lP(l)}{\sum_{l=min}^{N}P(l)}

対角線の長さ分布のエントロピー：
CRの複雑さをしめす指標

ENTR = -\sum_{l=l_{min}}^{N}p(l)\ln p(l) \\
p(l) = \frac{P(l)}{N_{l}}：全体に占める長さlの対角線の割合

縦線による指標

リカレンスプロットの縦線をみる．まず，クロスリカレンスプロットから縦線の長さ**ヒストグラムP(v)**を作成する．その後，それを用いた指標について検討する．

P(v)=\sum_{i,j=1}^{N}(1-CR_{i,j-1})(1-CR_{i,j+v})\prod_{k=0}^{v-1}CR_{i,j+k} \\
(1-CR_{i,j-1})：長さｌ未満はカウントしない \\
(1-CR_{i,j+v})：長さｌ以上はカウントしない \\
\prod_{k=0}^{l-1}CR_{i,j+k}：(i,j)からはじまる長さVの縦線の間のすべての点がプロットされているならカウントする \\

縦線上の再帰率(LAM:laminarity)：
v_min以上の長さを持つ縦線を形成するリカレンスプロットの割合（＝孤立していないプロットの割合）を示す．

　LAM = \frac{\sum_{v=v_{min}}^{N}vP(v)}{\sum_{v=1}^{N}vP(v)}　\\
v_{min}：最低限の長さを決める閾値パラメータ．

縦線の平均長さ(TT:traptime)：
システムが同じ状態で停留している時間を示す．

TT = \frac{\sum_{v=v_{min}}^{N}vP(v)}{\sum_{v=min}^{N}P(v)}

これらの指標を用いて時系列データを解析する．

まとめ

久しぶりに数式と向き合った事に気づきました．．．
理論のアイデアは，数式の見た目よりは直感的だと思います．
今度余力があるときに実践編も書きたいと思います．

参考

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up