はじめに
本記事では、関数型言語に触れているよくでてくる モナド について書きます。モナドとは何かを説明したり理解することは割と難しいと思うのですが、その理由の一つとしては、モナドという概念が 数学 の圏論に由来しているということにあると思います。何年も前にモナドを理解するために圏論を勉強したりしてみましたが、その中に出てくるモナドと、プログラミングにおけるモナドが本当に同じものなのか、というのはしばらく疑問でした。あるとき、Stateモナド(状態モナド) を具体例として、それを数学的な定義に基づいて実装してみたことで、プログラミングと数学の関係がより明確になってモナドの理解が深まったように思うので、この機会にまとめてみます。
プログラミングと数学が密接に関係する面白い例の一つだと思うのですが、記事が長くなってしまいモナドについて興味がないと読むのは大変だと思います。適当に斜め読みしてもらってその雰囲気だけでも伝えられれば幸いです。
Stateモナド(状態モナド)の数学の定義として参考にしたのは、Wikipediaに記載される、以下の一文です。
圏論的な見方では、状態モナドはデカルト閉圏の定義に現れる積函手と指数函手の随伴から作られる。
この一文を手掛かりに数学的にモナドを実装していきます。Haskell の基礎知識を前提としていますのでご了承ください。
まず State モナドとは何か、についてですが、Haskell では以下のように定義できるものです。
data State s x = State { runState :: s -> (x, s) }
instance Monad (State s) where
m >>= k = State $ \s ->
let (x, s0) = runState m s
in runState (k x) s0
return x = State $ \s -> (x, s)
1行目は、State という名前の型を新たに定義しているところで、型 s から 型 (x, s) への関数、という意味の、s -> (x, s) の部分が State モナドの実体です。s や x には任意の型(例えば Int型や String型など) を指定できます。(x, s)は数学でいうところの直積、プログラム(例えばpython)の用語でいうところのタプルに相当するものです。3行目以降の実装で、State を Haskell におけるモナドとして扱えるようにしています。
State モナドを使うと、値の変更を許さない純粋関数型言語においてあたかも "可変な" 状態が扱えるかのうように、プログラムを書くことができます。といっても、State モナドを知らない人にとってこの説明では意味が分からないと思うので、以下に使用例を示します。
1度の通過では入力値をそのまま返し、2度通過することで入力値に1を足した値を返すゲートを考えます。(通過回数は2回でリセット)。これは通過回数を記録できる"状態"を持たせることで実現できます。

このような性質を持つゲートを5つつなげたときに、入力値に対してどのような値を返すかを状態モナドを使ってシミュレートしてみます。(答えは簡単で、入力値+2が出力値となります)

Haskellでの実装例が以下です。
import System.Environment
data State s x = State { runState :: s -> (x, s) }
instance Monad (State s) where
m >>= k = State $ \s ->
let (x, s0) = runState m s
in runState (k x) s0
return x = State $ \s -> (x, s)
get = State $ \s -> (s, s)
put s = State $ \_ -> ((), s)
-- 2回通らないと1増えないゲートを再現
gate x = do
state <- get -- 現在の状態(Bool値)を取得
put (not state) -- 状態を(Bool値を反転させて)更新
return $ if state then (x + 1) else x -- 2回目(True)なら +1, 1回目(False)ならそのまま
-- 5つのゲートの連結を表現
five_gates x = return x >>= gate >>= gate >>= gate >>= gate >>= gate
main = do
input <- fmap (read . head) getArgs
putStrLn $ show . fst $ runState (five_gates (input :: Int)) False
-- ~~~~~ ~~~~~
-- 入力値(Int型) 初期状態
get は現在の状態を取得する関数で、put は状態を新しい値で更新する関数です。gate は図のゲートを再現したものです。内部状態である通過回数をBool値で表現していて、1回目の通過をFalse、2回目の通過を True と扱っています。gate 関数では、現在の状態(Bool値)を get で取得し、それを反転(True -> False, False -> True)させたものを新たな状態として put で保存しておきます。get で取得した状態が True であれば 2回目の通過とみなして入力値+1を出力として返し、そうでなければ1回目の通過とみなして入力値をそのまま返します。five_gates 関数で、gate を図のように5つ連結して、runState で状態モナドを実行しています。
最終結果は入力値(input)に対して +2 した値になるはずで、実際に上記を実行すると、入力+2の値が出力されます。
説明を簡単にするためにあまり使い道のない例を示しましたが、関数型言語の世界においては Stateモナドは入門書などでも紹介される代表的なモナドの一つであり、数学と密接に関わっており、(例えばリストモナドのように)単純すぎる例でもないため、数学との関係の理解を深める例として最適だと思い選びました。
本記事では、まず、数学的なベースとなる圏論について触れ、数学におけるモナドとは何かを説明して、その数学的な定義から Haskell での状態モナドを構築します。それが上記の State モナドと同じようにふるまうことを確認します。圏論に関しては以下の 圏論の基礎 を参考にしました。

圏論(数学)におけるモナドの定義
圏とは
まず、圏論における 圏 を定義します。
圏の定義: 圏は対象(各対象を $a, b, c, \cdots$などで表す) の集まりと、対象の間の射(対象 $a$ から対象 $b$ への射を $f:a \to b$のように書く)の集まりから成るもので、以下を満たすものである。
- 任意の射 $f : a \to b$, $g : b \to c$に対して、射の合成 $g \circ f : a \to c$が定義される。
- 任意の射 $f: a \to b, g :b \to c, h : c \to d$ に対して、$ (h \circ g) \circ f = h \circ (g \circ f) $が成り立つ
- 任意の対象 $a$ に対して、(恒等射と呼ばれる) 射 $\rm id_{\it a} : \it a \to a$ が存在して、任意の射 $f : a \to b$, $g : c \to a$ に対して、$f \circ \rm id_{\it a} = \it f$, $ { \rm id }_a \circ g = g$が成り立つ
一般的な圏のイメージを以下に示します。$C$は圏の名前です。 対象 を黒い点、 射 を矢印で表しています。圏の定義を満たすために必要な射(例えば恒等射など)をすべて図に描いているわけではないのでご注意ください。

上記の圏の定義を満たすものは無数にありますが、代表的なものとして、全ての(小さな1) 集合から成る圏 $\bf Set $があります。$ \bf Set $の対象は集合、射は集合から集合への全ての写像です。 $\bf Set$は全ての集合を含む圏なので、例えば、プログラミングで扱うInt型、Bool型、Char型、String型(=[Char]型)、そのリストやタプル、構造体、共用体、あるいは関数の型など、あらゆる型(の値の集合)を圏$\bf Set $の対象としてみなすことができます。また、プログラミングにおける関数は、圏論における射に相当します。ただし、ここで言う関数とは、一般の(c言語などの)プログラミング言語の関数の概念を全て含むものではなく、同じ入力(引数)を与えれば必ず同じ出力(返り値)を返す関数に限られます。
圏${\bf Set}$とプログラミングとの対応の大雑把なイメージ:

函手と自然変換
複数の圏があるときにそれらを関連付ける概念として、函手 というものがあります。
函手の定義: 圏$C$, $D$が与えられたとき、函手$T$は、$C$の各対象$a$を$D$の対象$T_a$に割り当て、$C$の各射 $f: a \to b$ を $D$の射 $Tf: Ta \to Tb$に割り当てるもので、以下を満たすものである。
$$ T( { \rm id_{\it a} }) = { \rm id_{\it T a} }, \hspace{5pt} T ( g \circ f ) = Tg \circ Tf \tag{1} $$

函手に相当するものとして、 Haskell には Functor があります。
class Functor t where
fmap :: (a -> b) -> t a -> t b
Functor は (a -> b) -> t a -> t b 型のfmap という名前のメソッドを一つ持ちます。このtを函手$T$だと解釈すれば、fmapは上図のように、対象$a$から対象$b$への射$f$ (f :: a -> b)を与えると、$T a$ から $T b$ への射 $T f$ (fmap f :: t a -> t b) を返すもの、とみなすことができます。つまり、Functor は上の図のような働きをするので、数学での函手に相当すると言えます。
なお、Haskell で Functorを定義する場合には式 (1) の関係を満たしていることまでは要請していないので、Functorクラスのインスタンスは必ずしも数学的な意味の函手ではありません。
函手が複数与えられたときに、それらを関係づける概念として 自然変換 とよばれるものがあります。
自然変換の定義:
圏$C,D$と、二つの函手$S, T:C \to D$が与えられたとき、自然変換 $\tau : S \xrightarrow{.} T$ とは、$C$の各対象$c$に$D$の射$\tau_c = \tau c: S c \to T c$を割り当てる関数で、$C$のすべての射$f: c \to c^\prime$について図式
\begin{CD}
c @. @. Sc @>{\tau c}>> Tc \\
@V{f}VV @. @V{Sf}VV @V{Tf}VV \\
c^\prime @. @.Sc^\prime @>{\tau c^\prime}>> T c^\prime
\end{CD}
が可換になるようなものである。
函手を別の函手に対応させる何か、という意味で、自然変換は以下の図のようなイメージです。

自然変換は「垂直」合成と「水平」合成を考えることができます。
図の$A,B,C$は圏、$\sigma, \tau, \sigma^{\prime}, \tau^{\prime}$は自然変換です。垂直合成とは、上図で示すところの、$\sigma$ と $\tau$、あるいは、$\sigma^{\prime}$ と $\tau^{\prime}$ を合成して得られる自然変換であり、それぞれ、$\tau \cdot \sigma$、$\tau^{\prime} \cdot \sigma^{\prime}$ と書きます。また、水平合成とは、上図で示すところの、$\sigma$ と $\sigma^{\prime}$ (あるいは、$\tau$と$\tau^{\prime}$など)を合成して得られる自然変換であり、その合成を、$\sigma^{\prime} \circ \sigma$、あるいは $\circ$ を省略して単に $\sigma^{\prime} \sigma$ と書きます。水平合成と垂直合成に関しては、以下の相互交換法則が成り立ちます(証明は省略します)。
(\tau^\prime \cdot \sigma^\prime) \circ (\tau \cdot \sigma) = (\tau^\prime \circ \tau) \cdot (\sigma^\prime \circ \sigma) \tag{2}
以降では、函手 $S:C \to B$に対して、(圏$B$の対象の恒等射を割り当てる)恒等自然変換 $ \varsigma : S \xrightarrow{.} S $ を、単に$S$と書くことにします。恒等自然変換は垂直合成 $\cdot$ について恒等射です($S \cdot \sigma = \sigma \cdot S = \sigma$)。また、恒等函手 $I_B: B \to B$ の恒等自然変換 $1_B : I_B \xrightarrow{.} I_B $は、水平合成 $\circ$ について恒等射です($1_B \circ \sigma = \sigma$, $\sigma^{\prime} \circ 1_B = \sigma^{\prime}$)。
Hom 集合
圏 $C$ の対象 $a, b$について、hom集合と呼ばれる、$a$ から $b$ への射全体を表す集合を ${\rm hom}_{C} (a, b)$ あるいは $C(a, b)$ と表現します。圏$C$を省略して${\rm hom} (a, b)$ と表記することもあります。参考にした圏論の書籍での表記とは異なりますが、Haskell における a -> b のような型の書き方に似せて、上記の表記の他に、本記事では hom集合を $a \to b$ のように表記することもあります。 $\bf Set$ における任意の ${\rm hom} (a, b)$ は (射の"集まり"という意味で1つの集合であるため) $\bf Set$の対象として扱えます。
プログラミングの言葉を使うと、例えば ${\rm hom} (\text{Int}, \text{String})$ あるいは $\text{Int} \to \text{String}$ と書かれた hom 集合は、$\text{Int}$型の値を引数として受け取って$\text{String}$型の値を戻り値として返す関数を、もれなくすべて集めた集合を意味します。
随伴
少し難しい概念ですが、 随伴 を定義します。
随伴の定義: $ A $ と $ X $ を圏とする。$ X $ から $ A $ への随伴とは、次の条件を満たすような三つ組み $ \langle F, G, \phi \rangle : X \rightharpoonup A $である。ここで、$ F $ と $ G $ は函手
X \overset{F}{\underset{G}{\rightleftarrows}} A
であり、$ \phi $ は対象 $ x \in X $ と $ a \in A $ による各組に集合間の 全単射
\phi = \phi_{x,a} : A(Fx, a) \cong X(x, Ga) \tag{3}
で $ x $ と $ a $ において 自然 なものを割り当てる関数である。
Hom集合のおさらいですが、$A(Fx, a)$ は、圏$A$における 対象 $Fx$ から 対象$a$への射全体の集合を意味し、${\rm hom}_A(Fx, a)$あるいは$Fx \to a$とも書かれるものです。また、$x$ と $a$ において 自然 とは、$k:a \to a^{\prime}, h:x^{\prime} \to x$ に対して以下の可換図式が成り立つことです。
\begin{CD}
A(F x, a) @>{\phi}>> X(x, G a) @. A(F x, a) @>{\phi}>> X(x, G a) \\
@V{k_*}VV @V{(Gk)_*}VV @V{(Fh)^*}VV @V{h^*}VV \\
A(F x, a^{\prime}) @>{\phi}>> X(x, G a^{\prime}) @. A(F x^{\prime}, a) @>{\phi}>> X(x^{\prime}, G a)
\end{CD}
上記の可換図式を、$f : Fx \to a$に対して、数式で表すと以下のようになります。
\phi (k \circ f) = Gk \circ \phi f,\hspace{5pt} \phi (f \circ F h) = \phi f \circ h \tag{4}
随伴の定義から、以下の定理を導くことができます。
定理: 随伴 $\langle F, G, \phi \rangle $は以下のものを決定する。
(i)各 $f : Fx \to a$の右随伴射が
\phi f = Gf \circ \eta_x : x \to Ga
であるような自然変換 $\eta: I_X \xrightarrow{.} GF$。
(ii)各$g:x\to Ga$が左随伴射
\phi^{-1}g = \varepsilon_a \circ Fg : Fx \to a
を持つような自然変換 $\varepsilon : FG \xrightarrow{.} I_A$。
さらに、次の両方の合成は(それぞれ$G$ および$F$の)恒等変換である。
G \xrightarrow{\eta G} GFG \xrightarrow {G \varepsilon } G,
F \xrightarrow{F \eta} FGF \xrightarrow {\varepsilon F } F \tag{5}
$\eta$を随伴の単位元と呼び、$\varepsilon$を余単位元と呼ぶ。
証明は以下の通りです。まず定理の(i)についてですが、$\eta_x = \phi( \rm id_{\it Fx}) $で定義すると、($k:=f, f:= \rm id_{\it Fx} $と置いて)随伴の定義である式 (4) より 、 $ \phi f = G f \circ \eta_{x} $ は明らかです。また、この結果を用いて、$h:x \to x^{\prime}$に対して、
\begin{align}
GFh \circ \eta_{x} &= \phi(Fh) \\
&= \phi({\rm id}_{Fx^{\prime}} \circ Fh) \\
&= \phi({\rm id}_{Fx^{\prime}}) \circ h \\
&= \eta_{x^{\prime}} \circ h
\end{align}
が成り立つ、すなわち以下の可換図式が成り立つので、$\eta: I_X \xrightarrow{.} GF$ は自然変換です。
\begin{CD}
x @. @. I_X x @>{\eta_{x}}>> GF x \\
@V{h}VV @. @V{I_X h}VV @V{GF h}VV \\
x^{\prime} @. @. I_X x^{\prime} @>{\eta_{x^{\prime}}}>> GF x^{\prime}
\end{CD}
定理の(ii)についても、$\varepsilon_a = \phi^{-1}({\rm id}_{Ga})$ とおいて、上と同様に証明できます。また、定理の (i) の結果を用いて、
\begin{align}
(G \varepsilon \circ \eta G)_a &= G \varepsilon_a \circ \eta_{Ga} \\
&= \phi(\varepsilon_a) \\
&= {\rm id}_{Ga}
\end{align}
より、$G \varepsilon \circ \eta G$は恒等変換です。$\varepsilon F \circ F \eta$が恒等変換であることも同様に示すことができます。以上で定理の証明は終わりです。
| 単位元 $\eta$ の定義のイメージ | 余単位元 $\varepsilon$ の定義のイメージ |
|---|---|
 |
 |
これで、冒頭のWikipediaの一文
状態モナドはデカルト閉圏の定義に現れる積函手と指数函手の随伴から作られる。
の 随伴 の部分の意味が明らかになりました。この一文を読み解くためには、"随伴"以外の部分の意味を明らかにする必要があります。
この一文のうち、状態モナドの数学的な定義として重要なのは、後半の「積函手と指数函手の随伴から作られる」の部分です("デカルト閉圏の定義に現れる"の部分は参考程度の情報です)。そのため、次に、まだ説明していない「積函手」と「指数函手」について定義して、それらが随伴であることを確認します。
積函手と指数函手
これ以降扱う圏は、はじめの方で紹介した圏$ { \bf Set }$ (すべての集合から成る圏)とします。
積函手 は、対象を適当な対象$s$との直積(デカルト積、カルテシアン積とも呼ばれ、プログラミングではタプルに相当)に移す函手です。具体的には、積函手を、以下を満たすような函手 $\hspace{5pt} \cdot \times s : { \bf Set } \to { \bf Set }$ であると定義します。
- 対象(集合) $a$ を $a \times s$ に移す
- 射 $f: a \to b$ を $\hspace{3pt} ( f, { \rm id }_s ) : a \times s \to b \times s : ( \tilde{a}, \tilde{s} ) \mapsto ( f(\tilde{a}), \tilde{s} ) $ に移す
($f$を、積函手によって、タプルの1番目の要素にのみ$f$を適用するような関数に移す、というイメージです)
このように定義した"積函手"が本当に函手であることを確認するため、上記の対応を $F$とおいて($F= \hspace{2pt} \cdot \times S$です)、式(1)の関係を満たしていることを確認します。$\tilde{a}\in a, \tilde{s} \in s$に対して、
\begin{align}
F ({\rm id}_a) (\tilde{a}, \tilde{s}) &= ({\rm id}_a(\tilde{a}), \tilde{s}) \\
&= (\tilde{a}, \tilde{s})
\end{align}
より、$F (\rm id_{\it a} ) = id_{\it F a}$ です。また、
\begin{align}
F(g \circ f) (\tilde{a}, \tilde{s}) &= (g \circ f(\tilde{a}), \tilde{s}) \\
&= Fg (f(\tilde{a}), \tilde{s}) \\
&= Fg (Ff (\tilde{a}, \tilde{s})) \\
&= (Fg \circ Ff)(\tilde{a}, \tilde{s})
\end{align}
より、$F(g \circ f) = Fg \circ Ff$が成り立ちます。式(1)を満たすことが確認できるため、上記の対応$F$は函手です。
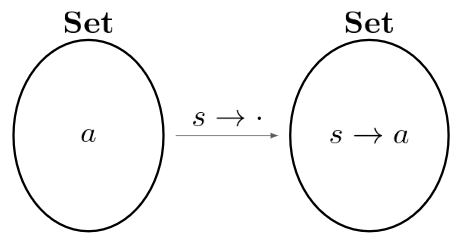
指数函手 は、対象を適当な対象$s$からの hom 集合に移す函手です。具体的には、指数函手を、以下を満たすような函手 $\hspace{5pt} s \to \cdot : { \bf Set } \to { \bf Set }$であると定義します。
- 対象(集合) $a$ を hom 集合 $s \to a \hspace{5pt} (= {\rm hom} (s, a))$ に移す
- 射 $f: a \to b$ を $\hspace{3pt} {\rm hom} (s, f) : {\rm hom} (s, a) \to {\rm hom} (s, b) : (k: s \to a) \mapsto (f \circ k)$ に移す
積函手の場合と同様に、このような対応を $G$ とおいて($G=s \to \cdot \hspace{2pt}$です)、$G$ が函手の定義(1)を満たしていることを確認します。 $k: s \to a$ に対して、
\begin{align}
G ({\rm id}_a) (k) &= {\rm id}_a \circ k \\
&= k
\end{align}
より、$G (\rm id_{\it a} ) = id_{\it G a}$ です。また、
\begin{align}
G (g \circ f) (k) &= (g \circ f) \circ k \\
&= g \circ (f \circ k) \\
&= Gg (f \circ k) \\
&= Gg (Gf(k)) \\
&= (Gg \circ Gf) (k)
\end{align}
より、$G(g \circ f) = Gg \circ Gf$が成り立ちます。やはり、式(1)を満たすため、上記の対応$G$も函手です。
本記事では見た目の分かりやすさから積函手、指数函手をそれぞれ $\cdot \times s, s \to \cdot$ と表記していますが、一般的な書き方ではないと思いますのでご注意ください。(指数函手という呼び方もGoogle検索であまりヒットしないため、一般的な呼び方ではない可能性があります。参考にした書籍では共変hom函手と呼ばれるものに相当します。)
式だけを見ると難しく見えますが、以下の図のようなイメージです。
| 積函手のイメージ | 指数函手のイメージ |
|---|---|
 |
 |
さて、次に、 積函手と指数函手が随伴になっていること(随伴の定義を満たしていること)を確認します。
随伴の定義に現れる圏$A$,$X$をいずれも$\bf Set$ に、函手$F, G$ をそれぞれ積函手、指数函手に置き換えて、これらが随伴の定義を満たしていることを確認します。具体的には、 各対象$x$, $a$ に対して式(3)の 自然な全単射
\phi=\phi_{x,a}: \hspace{4pt} (x \times s) \to a \hspace{3pt} \cong \hspace{3pt} x \to (s \to a) \tag{6}
が存在することを示すことで、積函手と指数函手が随伴であることを確認します。この全単射はカリー化(あるいはその逆)の考え方で構築できます。
より具体的には、$ f \in x \times s \to a$ に対して、$g=\phi(f) \in x \to (s \to a)$ を
\forall \tilde{x} \in x, \tilde{s} \in s, \hspace{10pt} g(\tilde{x})(\tilde{s}) = f(\tilde{x}, \tilde{s}) \tag{7}
によって定義することで、全単射$\phi$を得ることができます。$f=\phi^{-1}(g)$も上式の関係を使って得ることができます。この全単射が自然であること、すなわち式(4)を満たすことは、$k:a \to a^{\prime}$, $h:x^{\prime} \to x$, $f \in x \times s \to a$, $\tilde{x} \in x$, $\tilde{x}^\prime \in x^\prime$, $\tilde{s} \in s$ について以下が成り立つことから確認できます。
\begin{align*}
\phi(k \circ f) (\tilde{x})(\tilde{s}) &= k \circ f(\tilde{x}, \tilde{s}) \\
&= k (f(\tilde{x}, \tilde{s})) \\
&= k (\phi f(\tilde{x})(\tilde{s})) \\
&= k \circ (\phi f(\tilde{x})) (\tilde{s}) \\
&= Gk (\phi f(\tilde{x})) (\tilde{s}) \\
&= (Gk \circ \phi f)(\tilde{x})(\tilde{s}),\\
\end{align*}
\begin{align*}
\phi(f \circ Fh)(\tilde{x}^\prime)(\tilde{s}) &= f \circ Fh(\tilde{x}^\prime, \tilde{s}) \\
&= f(Fh (\tilde{x}^\prime, \tilde{s})) \\
&= f(h(\tilde{x}^\prime), \tilde{s}) \\
&= \phi f (h(\tilde{x}^\prime)) (\tilde{s}) \\
&= (\phi f \circ h) (\tilde{x}^\prime) (\tilde{s}).
\end{align*}
以上より、積函手と指数函手は随伴であることが確認できました。積函手と指数函手の随伴における、単位元$\eta$ と余単位元 $\varepsilon$ の定義については、以下のように可視化できます。$A, X$はそれぞれ圏$ { \bf Set }$です。
具体的に数式で書くと、$\eta_x : x \to (s \to (x \times s))$は、$\tilde{x} \in x, \tilde{s} \in s$ に対して、式(7)より
\begin{align}
\eta_x (\tilde{x})(\tilde{s}) &= \phi^{-1} (\eta_x) (\tilde{x}, \tilde{s}) \\
&= { \rm id } (\tilde{x}, \tilde{s}) \\
&= (\tilde{x}, \tilde{s}) \tag{8}
\end{align}
となり、また、$\varepsilon_a : ((s \to a) \times s) \to a$ は、$\tilde{h} \in (s \to a), \tilde{s} \in s$に対して、
\begin{align}
\varepsilon_a (\tilde{h}, \tilde{s}) &= \phi (\varepsilon_a) (\tilde{h}) (\tilde{s}) \\
&= { \rm id } (\tilde {h})(\tilde {s} ) \\
&= \tilde{h} (\tilde{s}) \tag{9}
\end{align}
となります。
以上で、
デカルト閉圏の定義に現れる積函手と指数函手の随伴
の部分は一通り説明しました。さて、ここでようやく、(数学的な)モナドの定義が現れます。
モナド
圏論におけるモナドの定義は以下の通りです。
モナドの定義: 圏$X$におけるモナド $ T=\langle T, \eta, \mu \rangle$は、函手 $T : X \to X $ と二つの自然変換
\eta: I_X \xrightarrow{.} T, \hspace {5pt} \mu : T^2 \xrightarrow{.} T \tag{10}
からなり、次の図式を可換にするものである。
\begin{CD}
T^3 @>{T_\mu}>> T^2 @. IT @>{\eta T}>> T^2 @<{T \eta}<< TI \\
@V{\mu T}VV @V{\mu}VV @| @V{\mu}VV @| \\
T^2 @>{\mu}>> T @. T @= T @= T
\end{CD} \tag{11}
Wikipediaの一文に戻ると、「積函手と指数函手の随伴」によってモナドを定義できるとありましたが、一般に、随伴によってモナド(モナドの定義を満たすもの)を構成できることが知られています。
随伴$\langle F, G, \phi \rangle $の単位元を$\eta$、余単位元を$\varepsilon$とすると、恒等自然変換($F:F \xrightarrow{.} F $ や $ G:G \xrightarrow{.} G$ など)が垂直合成に対して恒等的であることに注意して、(また水平合成の演算$\circ$を省略して書いていることにも注意して) 水平合成と垂直合成の相互交換法則 (2) から、
\begin{align}
\varepsilon \cdot FG \varepsilon
&= \varepsilon {\rm 1}_A \cdot FG \varepsilon \\
&= (\varepsilon \cdot FG)({\rm 1}_A \cdot \varepsilon) \\
&= \varepsilon \varepsilon \\
&= ({\rm 1}_A \cdot \varepsilon) (\varepsilon \cdot FG) \\
&= {\rm 1}_A \varepsilon \cdot \varepsilon FG \\
&= \varepsilon \cdot \varepsilon FG
\end{align}
が成り立ちます。すなわち、以下の可換図式が成り立ちます。
\begin{CD}
FGFG @>{FG \varepsilon}>> FG \\
@V{\varepsilon FG}VV @V{\varepsilon}VV \\
FG @>{\varepsilon}>> I_A
\end{CD}
この関係に左から函手$G$、右から函手$F$を合成した結果として(厳密に言えば式(2)の相互交換法則も用いて)以下が成り立ちます。
\begin{CD}
GFGFGF @>{GFG \varepsilon F}>> GFGF \\
@V{G \varepsilon FGF}VV @V{ G \varepsilon F }VV \\
GFGF @>{G \varepsilon F}>> GF
\end{CD}
また、随伴の定理で示した式(5)の恒等変換
G = G \varepsilon \cdot \eta G : G \xrightarrow{.} G, \hspace{10pt} F = \varepsilon F \cdot F \eta : F \xrightarrow{.} F
の性質より、以下の可換図式も成り立ちます。
\begin{CD}
I_X GF @>{\eta GF}>> GFGF @<{GF \eta}<< GF I_X \\
@| @V{G \varepsilon F}VV @| \\
GF @= GF @= GF
\end{CD}
$T :=GF$、$\mu := G\varepsilon F : GFGF (=T^2) \xrightarrow{.} GF (= T)$ とおくと、これはまさに、モナドの定義で示した式(11)の2つの可換図式を満たすことを意味します。すなわち、随伴$\langle F, G, \phi \rangle $があれば、モナド$ T=\langle T, \eta, \mu \rangle$を構築することができます。
これを「積函手と指数函手の随伴」にあてはめて、その結果得られるモナドを(数学的な意味での)状態モナドとして定義して具体的に書き下すと、以下のようになります。
状態モナドの自己函手$T: X \to X$ は、$T=GF$($T$は積函手と指数函手の合成)より、
Tx : s \to (x \times s)
です。これはちょうど、Haskell におけるStateモナドの型の定義部分である、
data State s x = State { runState :: s -> (x, s) }
に相当します。 また、自然変換 $\eta: I \xrightarrow{.} T, \hspace{5pt} \eta_x : x \to (s \to (x \times s))$ は、式(8) をそのまま使って、$\tilde{x} \in x, \tilde{s} \in s$に対して、
\eta_x(\tilde{x})(\tilde{s}) = (\tilde{x}, \tilde{s})
です。これは Haskell におけるStateモナドの定義の return x = State $ \s -> (x, s) に相当します。
自然変換 $\mu : T^2 \xrightarrow{.} T, \hspace{5pt} \mu_x: T^2 x \to T x$ については、式で表現しにくいですが、式(9)の関係を考慮すると、以下の図の青い枠と線で示すような$s$の適用によって得られる、$T^2 x = s \to ((s \to (x \times s)) \times s)$ から $Tx = s \to (x \times s)$ への射です。
$\mu_x$ は Haskell では join :: Monad m => m (m a) -> m a という関数に相当します。join は join x = x >>= id と定義できるもので、ここでは詳しく示しませんが、Stateモナドをあてはめて join の実装を評価すると、上図の$\mu_x$のふるまいと一致することが確認できます。 逆にjoin が定義されていれば、そこから >>= :: m a -> (a -> m b) -> m b を定義することができるので、このことを使って、以下で数学的な定義に基づいたState モナドを実装します。
数学的な定義に基づくStateモナドの実装
上記の(数学的な)状態モナドを Haskell で実装します。
数学的に構築する手順(ポイント)はざっくり以下になります。
- 積函手 $F$ と 指数函手 $G$ を実装する。
- $F, G$を合成して、自己函手 $T$ を実装する
- (自然な)全単射$\phi = \phi_{x,a} : (x \times s) \to a \hspace{2pt} \cong \hspace{2pt} x \to (s \to a)$ とその逆射 $\phi^{-1}$を実装する
- 恒等射 $\rm id $ を$\phi$や$\phi^{-1}$で移すことにより、自然変換 $\eta$と$\varepsilon$ を実装する
- 自然変換$\varepsilon$を使って、自然変換$\mu = G \varepsilon F$を実装する
- 自然変換$\eta$と自然変換$\mu$を使って、
Monadクラスのメソッドである、returnと>>=を実装する
まず、積函手$F$($=\cdot \times s$)の実装です。
data F s x = F { run_f :: (x, s) }
instance Functor (F s) where
fmap f (F (x, s)) = F (f x, s)
数学の定義の通り、対象 x が函手(Functor) F によって対象 (x, s) に、射 f :: x -> x' が函手 F によって射 (fmap f) :: (x, s) -> (x', s) に写されることを表現しています。
次に、指数函手$G$($= s \to \cdot$)の実装です。
data G s a = G { run_g :: (s -> a) }
instance Functor (G s) where
fmap f (G k) = G (f . k)
対象 a が G によって対象 s -> a に、射 f :: a -> b が函手 G によって射 (fmap f) :: (s -> a) -> (s -> b) に写されることを表現しています。
次に、自己函手$T$です。$T$は$GF$で定義できるので、
data T s x = T { run_t :: G s (F s x) }
instance Functor (T s) where
fmap f (T k) = T $ fmap (fmap f) k
となります。少々扱いが面倒になりますが、$GF$のセットで$T$であるということを強調するために、G s (F s x) を新しい型 T として定義しています。
次に、式(6) の $\phi, \phi^{-1}$ を実装します。$\phi$ を phi, $\phi^{-1}$を psi として定義します。
phi :: ((F s x) -> a) -> (x -> (G s a))
phi f = \x -> G $ \s -> f (F (x, s))
psi :: (x -> (G s a)) -> ((F s x) -> a)
psi g = \(F (x, s)) -> run_g (g x) s
今定義した phi, psi を用いて、$\eta_x =\phi(\rm id_{\it Fx})$, $\varepsilon_a =\phi^{-1}(\rm id_{\it Ga})$ を実装します。
eta :: x -> (G s (F s x))
eta = phi id
epsilon :: (F s (G s a)) -> a
epsilon = psi id
次に$\mu_x$ の実装です。
mu :: (T s (T s x)) -> T s x
mu ttx = T $ fmap epsilon $ fmap (fmap run_t) (run_t ttx)
この実装を右から読んでいくと、fmap (fmap run_t) (run_t ttx) は T s (T s x) 型の値である ttx から T を一旦はがして G s (F s (G s (F s x))) 型の値を得る操作です。その結果に fmap epsilon (+ 型推論) を適用することで、数学における $ G\varepsilon F$ を再現しています。この結果として得られる G s (F s x) 型の値に T をつけて、最終的に T s x 型の値を返します。
あとは、今までに定義した eta と mu を使って、Haskell における Monad として状態モナド T を実装します。
instance Monad (T s) where
return = fmap T $ eta
m >>= f = mu $ (fmap f) m
これで、積函手と指数函手の随伴として実装されるモナド (数学的に構築した状態モナド)が 完成 しました。
使いやすいように、get と put も定義します。
construct_t :: (s -> (x, s)) -> T s x
construct_t f = T $ fmap F (G f)
get_t :: T s s
get_t = construct_t $ \s -> (s, s)
put_t :: s -> T s ()
put_t s = construct_t $ \_ -> ((), s)
実際に使ってみます。
gate x = do
state <- get_t
put_t (not state)
return $ if state then (x + 1) else x
five_gates x = return x >>= gate >>= gate >>= gate >>= gate >>= gate
run_state t_monad s = run_f $ run_g (run_t t_monad) s
main = do
input <- fmap (read . head) getArgs
putStrLn $ show . fst $ run_state (five_gates (input :: Int)) False
これを ghc でコンパイルして実行すると、以下のようになります。
$ ghc math_state_monad.hs
[1 of 1] Compiling Main ( math_state_monad.hs, math_state_monad.o )
Linking math_state_monad ...
$ ./math_state_monad 10
12
$ ./math_state_monad 30
32
入力した値に対して、+2 した値が実行結果として返ってきます。積函手と指数函手の随伴で作ったモナドが、冒頭に示した State モナドの使用例と同じようにふるまっており、期待した結果となりました。
よくよく考えると当たり前なのかもしれませんが、随伴を使ってプログラムとして実際に動作する Stateモナドを実装できるのは面白いと思いました。これによって、プログラミングにおけるモナドと数学におけるモナドの関係をより明確にできたような気がします。
付録1 (ソースコード)
本文中で示した、数学的に構築した State モナドの実装を以下に載せておきます。
import Control.Applicative
import System.Environment
data F s x = F { run_f :: (x, s) }
instance Functor (F s) where
fmap f (F (x, s)) = F (f x, s)
data G s a = G { run_g :: (s -> a) }
instance Functor (G s) where
fmap f (G k) = G (f . k)
data T s x = T { run_t :: G s (F s x) }
instance Functor (T s) where
fmap f (T k) = T $ fmap (fmap f) k
phi :: ((F s x) -> a) -> (x -> (G s a))
phi f = \x -> G $ \s -> f (F (x, s))
psi :: (x -> (G s a)) -> ((F s x) -> a)
psi g = \(F (x, s)) -> run_g (g x) s
eta :: x -> (G s (F s x))
eta = phi id
epsilon :: (F s (G s a)) -> a
epsilon = psi id
mu :: (T s (T s x)) -> T s x
mu ttx = T $ fmap epsilon $ fmap (fmap run_t) (run_t ttx)
instance Monad (T s) where
return = fmap T $ eta
m >>= f = mu $ (fmap f) m
instance Applicative (T s) where
pure = return
g <*> m = g >>= flip fmap m
construct_t :: (s -> (x, s)) -> T s x
construct_t f = T $ fmap F (G f)
get_t :: T s s
get_t = construct_t $ \s -> (s, s)
put_t :: s -> T s ()
put_t s = construct_t $ \_ -> ((), s)
gate x = do
state <- get_t
put_t (not state)
return $ if state then (x + 1) else x
five_gates x = return x >>= gate >>= gate >>= gate >>= gate >>= gate
run_state t_monad s = run_f $ run_g (run_t t_monad) s
main = do
input <- fmap (read . head) getArgs
putStrLn $ show . fst $ run_state (five_gates (input :: Int)) False
付録2(モナドの解釈について)
モナドとは何かと聞かれれば、モナドの定義に従うもの、としか答えようがないと思いますが、それだけだとイメージが湧きにくいと思います。こちらの動画 で1:31:30 あたりから解説されている、計算作用(Computational effect)にモナドを利用する、という考え方が分かりやすかったので、特に「状態モナド」を「副作用」とみなす、という観点からモナドの解釈を書いてみます。自分なりの解釈なので、参考にさせていただいた動画やその動画で紹介される元の論文での説明と意味合いが異なる部分があるかもしれませんがご容赦ください。
数学で言うところの関数(圏論での射)は、
f : a \to b
のように書きます。関数 $f$は、入力として集合(圏論で言うところの対象) $a$の元を1つ与えると、出力として集合 $b$ の元を1つ返すものです。数学における関数は、同じ入力($a$の元)に対しては、必ず同じ出力($b$の元)を返します。一方で、一般的なプログラミング言語における"関数"は、(例えばグローバル変数などの影響よって)同じ入力を与えても同じ出力を返すとは限りません。同じ入力を与えても必ずしも同じ結果を返すとは限らない性質のことを副作用と呼ぶことにします。
数学で扱う関数には副作用はありませんが、あえて圏論の世界でプログラミングにおける副作用を表現するために、状態モナドの自己函手 $T$ を、ここでは「副作用」と解釈してみます。そして、型 $a$ の入力に対して、副作用 $T$ の影響を受けた型$b$ の出力を返す関数$f$ を
f: a \to T b
のように表現します。$f$に$a$の元を与えると$b$の元を返すが、その結果には副作用$T$が伴っている、という解釈です。冒頭で示した"ゲート"で例えると分かりやすいのではないかと思いますが、ゲート1つ1つはいずれも、Int 型の値を入力として、内部状態に依存する(副作用を伴った) Int 型の値を出力するので、上の式の $a$ と $b$ にいずれも Int があてはまるというイメージです。このような副作用$T$を持つ複数の関数
\begin{align}
f_0 &: a_0 \to T a_1, \\
f_1 &: a_1 \to T a_2, \\
f_2 &: a_2 \to T a_3, \\
\cdots\\
f_{n-1} &: a_{n-1} \to T a_n \\
\end{align}
が与えられたときに、$f_0, f_1, \cdots$ を直接合成することはできませんが、$f_k$ に函手$T^k$ ($k=0,1,\cdots,n-1$)を作用させた、
\begin{align}
f_0 &: a_0 \to T a_1, \\
T f_1 &: Ta_1 \to T^2 a_2, \\
T^2 f_2 &: T^2 a_2 \to T^3 a_3, \\
\cdots\\
T^{n-1} f_{n-1} &: T^{n-1} a_{n-1} \to T^n a_n \\
\end{align}
であれば以下のように合成できて、
T^{n-1} f_{n-1} \circ \cdots \circ T^2 f_2 \circ T f_1 \circ f_0 : \hspace{10pt} a_0 \to T^n a_n
結果として型 $a_0$ を受け取って型 $T^n a_n$ を返す関数が得られます。
出力の型 $a_n$ に作用している函手 $T^n$ は、一見すると、最初に副作用としてみなした $T$ とは別物の副作用として扱うべきもののように見えます。
ここで一旦モナドの定義を見直してみます。モナドの定義に現れる、式(10)、式(11)は、2つの同じ函手$T$の合成 $T^2 = T \circ T$を "結合" して函手 $T$ を得る手段 $\mu$ があり、その結果は"結合"の順序に依存しない、というように解釈できます。 $T^n = T \circ T \circ \cdots \circ T$ にあてはめると、左の式の任意の箇所の合成 $\circ$ から順次 $\mu$ により"結合" して、その結合の順序に依存しない形で、$T^n$ から $T$ への一意的な自然変換を得ることができます。
つまり $T$がモナドの函手であったことを思い出すと、$f_0, \cdots, f_{n-1}$ の合成によって最終的に得られる関数は、$\mu$ による"結合" も込みで、合成前の関数の形 $f : a \to T b$ になるということです。
以上をまとめると、状態モナドの自己函手 $T$ を副作用と解釈すれば、副作用を伴う計算は $f:a \to T b$ と表現でき、副作用のある計算が与えられたときにそこから副作用のない計算を得ること($a \to T b$ から $a \to b$ を得ること)はできませんが、そのような副作用を持つ計算同士であればそれらを好きなようにつなぎ合わせたより大きな計算を、同じ副作用の枠組みの中で新たに構築することができるので、圏論の世界で副作用を伴う計算をモデル化できていると言えるのだと思います。
上記は、$a$ から $b$ への関数の副作用を$T$を使って表現しているのであって、$f: a \to T b$ 自体は副作用のない数学的な意味での関数(圏論での射)であることに注意する必要があります。$f: a \to T b$ が圏論での射として扱えるために、純粋関数型言語である Haskell においても、(本物の)副作用を IO モナドという形で扱えているのだと思います。
■終わり■
-
「小さな集合」について。あまり詳しく説明はできませんが、「小さな」集合というときには、(有限集合のように)数の少ない集合のことを指すのではなく、自然数全体の集合や実数全体の集合などのような無限集合も含みます。集合論における標準的な演算で閉じている十分大きな集合である「ユニバース」が存在すると仮定して、集合がそのユニバースのメンバであるときに「小さな集合」と言うらしいです。プログラミングで扱う範囲では特に気にする必要はない(プログラミングで扱う型・関数はそのユニバースにすべて含まれていると考えてよい)と思うので、本文中では、本来「小さな」をつけるべきところでも、それを省略して書いています。 ↩


