More than 1 year has passed since last update.

BrainPad Advent CalendarAdvent Calendar 2021

@seth_ger

テネシー州の教育実験: STARの無作為性を検証する

AdventCalendar2021

Last updated at 2022-11-30Posted at 2021-12-24

このブログの内容は、2021年12月24日に投稿した記事について、下記を踏まえてテーマを変更して再度書き直したものとなっております。

経緯は下記のURLをご覧ください。

この度は多方面にご迷惑をおかけし、誠に申し訳ございませんでした。

1. はじめに

アメリカで実施されたSTAR(Student/Teacher Achievement Ratio)プロジェクトと呼ばれる、学級規模が及ぼす教育効果を検証した教育実験があります。本記事では、当該プロジェクトにおける介入割り当てや処置効果について、簡単に検証した内容をご報告いたします。

STARプロジェクトは、学級の人数規模が、学力傾向や意識傾向(心理尺度)にどのような影響をもたらすか」を検証するために、1980年代のアメリカ・テネシー州で、初等教育改革の一環として実施されました。
結果として、小規模学級に所属した学生の方が(特に低学年において)短期的、長期的に成績が良くなる傾向が確認されています。¹
実際に当プロジェクト以降、適切な学級規模を議論する上で少人数クラスの優位性を示す強い論拠となっているようです。²

本研究では、ある年度に入学した生徒たちに対して、幼稚園～小学校3年生の4年間にわたって、生徒を次の3種類のクラスにランダムに割り当てています。

・少人数クラス（教師1人に生徒13～17人）、
・通常クラス（教師1人に生徒22～25人）、
・通常補助員付きクラス（22～25人の生徒に専任の補助員が付く）

(なお、幼稚園での実験後、通常クラスと通常補助員クラスに差異が見られなかったため、補助員付きクラスの生徒はそれぞれ少人数クラスと通常クラスに一部振り分けているようです。本記事では、以降小規模クラス=処置群、通常クラスor通常補助員付きクラス=対象群として扱っていきます。)

一般に、実験の処置効果を判断する際に、対象を

処置群(なんらかの介入を行ったグループ。ここでは少人数クラス)
対象群(処置群への介入効果を定量的に測定するための基準となるグループ。ここでは通常クラスor通常補助員付きクラス)

のどちらかに割り当てて実験を行います。実験後、シンプルな統計的2群間比較を行うことで、処置効果を測定することができるようになります。

一方で、各群への割り当てに偏り(バイアス)が発生してしまった場合、単純な比較は成り立たなくなります。

例えば、「少人数クラスに対して、元々学力が高い生徒を割り当てる」「少人数クラスには、より熱心な教師を割り当てる」ような割り付けを行ってしまうと、少人数クラスの生徒群の方が（実際には少人数クラスそのものに教育的な効果がないにもかかわらず）高い教育効果がみられる、といった誤った結論を導いてしまうかもしれません。

本プロジェクトにおいても、実験期間中生徒と教師を各群にランダムに割り付ける(RCT: ランダム化比較試験)ことで、「選択バイアス」の発生を回避しているようです。

ただ、実際には選択バイアスを完全に制御することは難しいとされています。
本プロジェクトにおいても、実際には完全なRCTにはなっていないのではないか、という指摘もされています。³

本ブログ記事では、実験後公開されているデータ(学生と教師のデモグラフィックデータと、教育効果を測定するための各種学力テスト等の成績情報)を元に、

データセットの概観・可視化
(STARプロジェクトをRCTとみなしたときの)処置効果の確認
選択バイアスの確認
傾向スコアによる補正等を行った際の介入効果(大人数クラスに対する小規模クラスの教育効果)の確認

を実施していきます。

2. データセットの概観、可視化

実験において取得されたデータは下記URLにおいてパブリックドメインで公開されており、

・Tennessee's Student Teacher Achievement Ratio (STAR) project
https://dataverse.harvard.edu/dataset.xhtml?persistentId=hdl:1902.1/10766

主に

実験期間中(幼稚園から小学3年生まで)に取得された、心理尺度(自己概念、動機付け)に関する測定結果や、SAT学力テストなどの結果
フォローアップ期間(高校卒業時まで)の、介入の持続的効果を測定するためのデータ。各都市の学力テストの結果や、科目などの履修状況、高校進学有無、大学入試の参加状況と得点　等
生徒・教師・学校のデモグラフィック情報(生徒・教師の人種・性別、学校の都会度・規模など)

等の情報が確認できます。

本データセットは下記の4つのtabファイルから構成されています。

STAR_Students.tab
- 学生・教師に関するデモグラフィックデータ、学年ごとの各種心理尺度、学力テスト結果等
STAR_K-3_Schools.tab
- STAR実施期間中(幼稚園(GK)から3年生(G3))までの学校情報
- 上記STAR_Students.tabと学年別の学校ID情報(G[x]SCHID)で結合する
STAR_High_Schools.tab
- フォローアップ期間中に生徒が所属した高校の情報
- 本記事では利用しません
Comparison_Students.tab
- STARに参加しなかったテネシー州の他学校生徒のデモグラフィックデータ、各種心理尺度、学力テスト結果等
- 本記事では利用しません

tabファイルには列情報が存在しませんが、上記ページからダウンロードできる「starUsersGuide.pdf」に
各ファイルごとの列名や詳細情報が記載されているので、それを元に列情報を付与しております。

なお、データの加工や実際の集計可視化の過程については、下記のgithubページに公開しておりますので、
詳細を知りたい方はご確認ください。

データ概観

本件に参加した学生データは、11,601件のレコードと、379個の変数で構成されています。
1学生ごとに1レコードとなっており、デモグラフィック情報や各学年ごとの学校・教師、高校までの成績データなどを横持ちで保持しています。
なお、個々の学生が所属した学校に関するデモグラフィックデータは、各学年ごとに個別に持っている学校ID(G[x]SCHID)をキーに、STAR_K-3_Schools.tabと紐づけることで取得可能です。

実験期間について

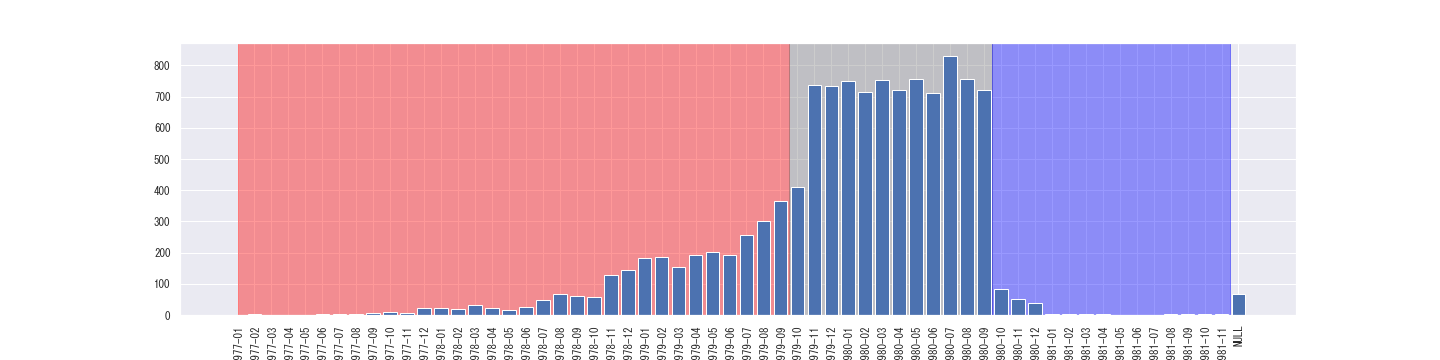
STARプロジェクトは1985年から始まった4年間のプロジェクトになっていますが、各生徒が毎年STARプロジェクトに参加しているわけではありません。

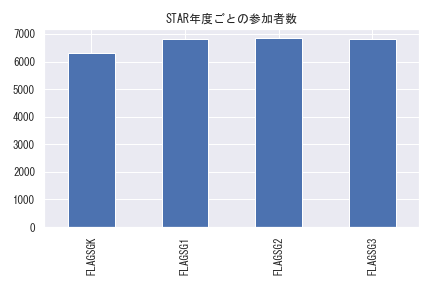
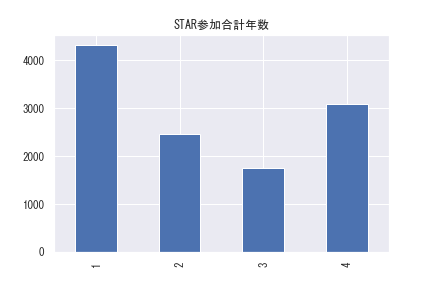
延べ1万人以上参加していますが、各年度ごとのSTARプロジェクト参加者数はおよそ6,000～7,000人程度で、生徒単位でみた4年間における合計プロジェクト参加年数もバラついていることが分かります。

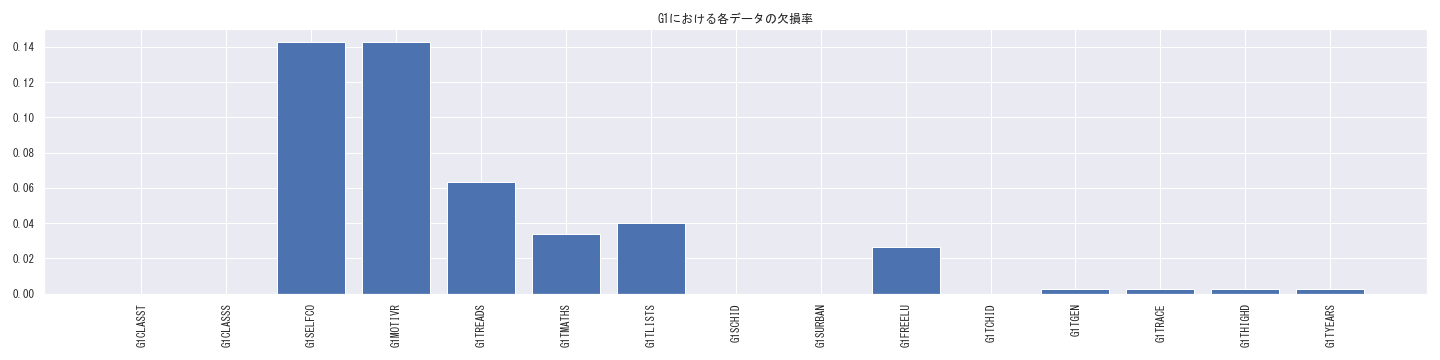
各列のデータ欠損について

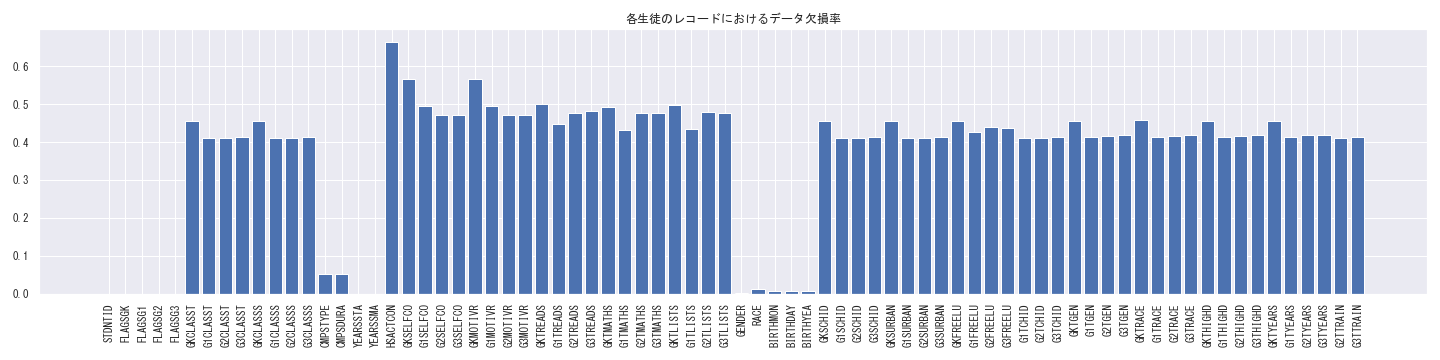
各学年の成績データや心理尺度データをみると、データ欠損が発生していることが分かります。

欠損理由の多くは、「STARプロジェクトに参加していない年度のデータが取得できない」ことによるものですが、
上記のようにSTARプロジェクト参加年度であっても、処置効果に関する変数(GxSELFCO・GxMOTIVR(x年次の心理尺度), GxTREADS, GxTMATHS, GxTLIST(x年次の学力テスト結果))や、デモグラフィック変数(G[x]FREELU等)の双方に1~20%程度の欠損があることが分かります。

(後述しますが、欠損原因が不明である欠損データについては、単純に削除や穴埋めをするだけでは問題が発生する可能性があります。)

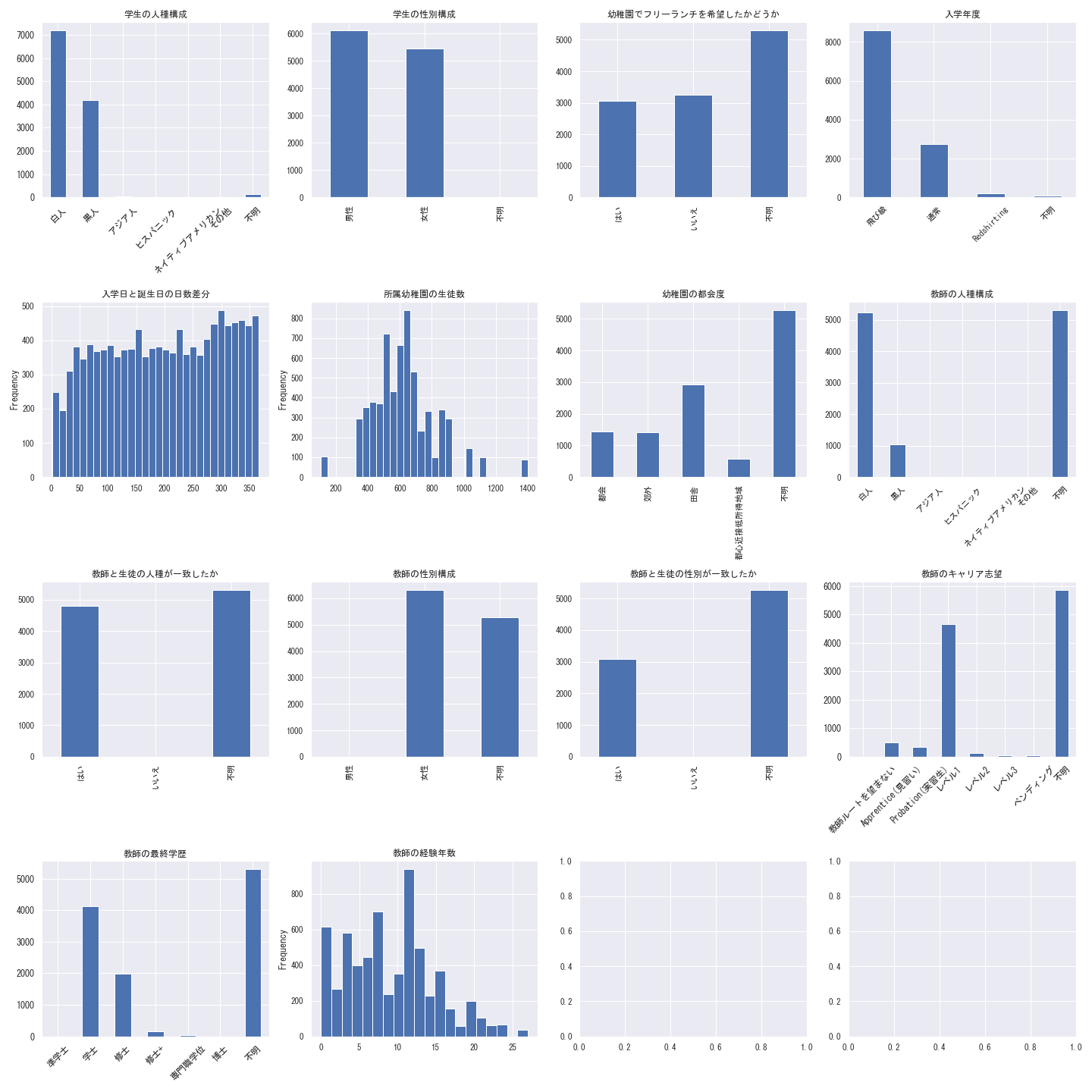
デモグラフィック変数

次に、デモグラフィックデータを確認していきます。

STAR開始年度は1985年であり、アメリカの幼稚園は満5歳での入学となることから、
通常であれば1979年10月から1980年9月までの生まれの子供が入園することになります。

一方で、実際に生徒の誕生日の内訳を確認すると、上記年度の前後年に生まれた学生も参加していることがわかります。

アメリカでは、日本と異なり
・Academic Redshirting (意図的な入学時期の遅れ)
・Grade Skipping(飛び級)
と呼ばれる、入学年度の「ずらし」が行われています。

Redshirtingは(下降傾向ではあるものの)およそ学生の14％、Grade Skippingは1%程度行われているようで³、本データの傾向とも乖離しません。

上記のような入学年度の「ずらし」は学力に影響がある可能性が高く⁴、また、同一年度内においても、早生まれ・遅生まれが学力に影響を与える可能性があります。⁵

このような、特に学力に影響を及ぼす可能性があり、介入群と対象群で分布が異なる可能性があるデモグラフィック変数については処置群・対象群間で偏りがないかを確認したほうが良いと思われます。

その他学力と介入割当に影響する可能性があるデモグラフィック変数を下記にまとめました。

特徴量	取得元ファイル	列名	変数の型	備考
性別	STAR_Students.tab	GENDER	カテゴリ変数	1: 男性 2: 女性
人種	STAR_Students.tab	RACE	カテゴリ変数	1: 白人 2: 黒人 3: アジア人 4: ヒスパニック 5: ネイティブアメリカン 6: その他
フリーランチの希望有無	STAR_Students.tab	G[x]FREELU	カテゴリ変数	1: 有 2: 無
入学年度	STAR_Students.tab	加工データ(ENTRANCE_GRADE)	カテゴリ変数	0: Grade Skipping(飛び級) 1: Academic Redshirting (意図的な入学時期の遅れ 2: それ以外
入学基準日からの経過日数	STAR_Students.tab	加工データ(DATEDIFF_FROM_ENTRANCE_DATE)	数値変数	テネシー州での入学基準日(cut-off-date)⁶である9/30からの日数差分
学校規模(該当学年における在籍者数)	STAR_K-3_Schools.tab	G[x]ENRMNT	数値変数
幼稚園時のデータを取得できるかどうか	STAR_K-3_Schools.tab	FLAGGK	カテゴリ変数	STAR実施時、テネシー州において幼稚園入園は義務教育ではなかったため、幼稚園時のデータを利用できるかどうかによって「幼稚園に行っていたかどうか」を間接的に確認する
所属する学校の都会度	STAR_Students.tab	G[x]SURBAN	カテゴリ変数	1: URBAN(都会) 2: SUBURBAN(郊外) 3: RURAL(田舎) 4: INNERCITY(都心近接低所得地域)
過去のSTARプロジェクト参加年度における小規模クラス経験回数	STAR_Students.tab	加工データ	数値変数	幼稚園時は取得できないので除く
担当教師の性別	STAR_Students.tab	G[x]TGEN	カテゴリ変数	1: 男性 2: 女性
担当教師の性別が生徒の性別と一致するかどうか⁷⁸	STAR_Students.tab	加工データ	カテゴリ変数	1: はい 2: いいえ
担当教師の人種	STAR_Students.tab	G[x]TRACE	カテゴリ変数	カテゴリ名は上記「人種」列と同一
担当教師の人種が生徒の人種と一致するかどうか⁹	STAR_Students.tab	加工データ	カテゴリ変数	1: はい 2: いいえ
担当教師のキャリア志望	STAR_Students.tab	G[x]TCAREE	カテゴリ変数	1: 教師になることを望まない 2: Apprentice(見習い) 3: Probation(実習生) 4: キャリアラダー: レベル1 5: キャリアラダー: レベル2 6: キャリアラダー: レベル3 7: ペンディング
担当教師の最終学歴 ¹⁰	STAR_Students.tab	G[x]THIGHD	カテゴリ変数	1: 準学士 2: 学士 3: 修士 4: 修士+ 5: 専門職学位 6: 博士
担当教師の経験年数 ¹¹	STAR_Students.tab	G[x]TYEARS	数値変数

(列名に含まれる[x]には、それぞれK, 1, 2, 3のいずれかが入り、STARの参加年度を表します。Kは幼稚園(Kindergarden)時、1, 2, 3はそれぞれ小学1, 2, 3年生時の情報を意味します。)

次に、目的変数(処置効果)について確認していきます。
前述の通り、STAR期間中から高校生に至るまで年次で様々な学力テスト、心理尺度テストの結果等を取得しています。

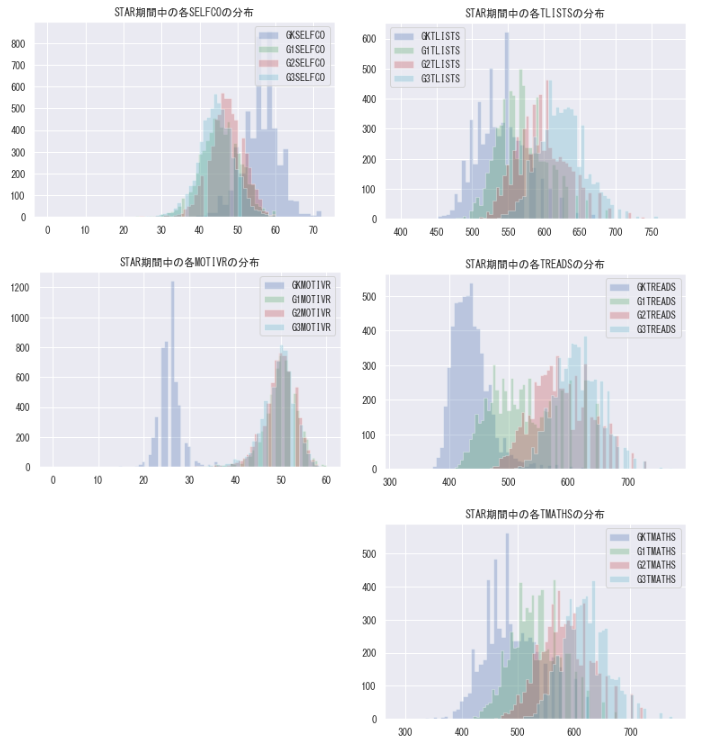
まず、短期的な結果については、(STAR期間中x年次に取得した心理尺度(G[x]SELFCO, G[x]MOTIVR)、SAT学力テスト結果(G[x]TLISTS, G[x]TREADS, G[x]TMATHS)の5つについて確認していきます。

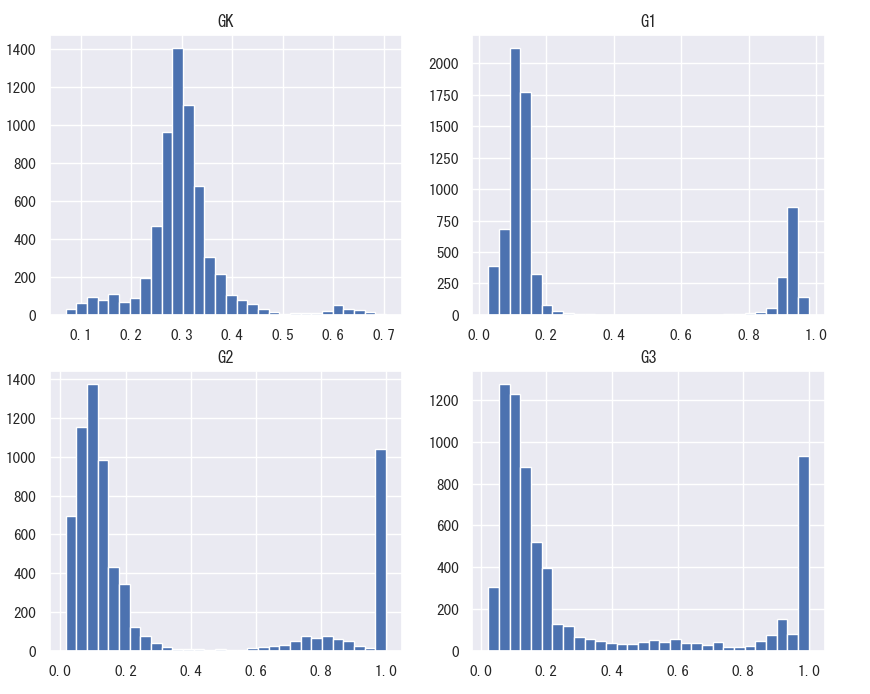
各学年ごとの目的変数を見ると、下記のような特徴があることがわかります。

心理尺度系の目的変数は、幼稚園時は高いが、小学校1～3年ではほぼ平均が変わらない傾向がある
SAT学力テスト系の目的変数は、学年次が上がるにつれて分布が右にズレていく(平均が高くなる)傾向がある
学力テスト系は特に、学年間では比較せず、学年ごとに比較するのがよさそうです。

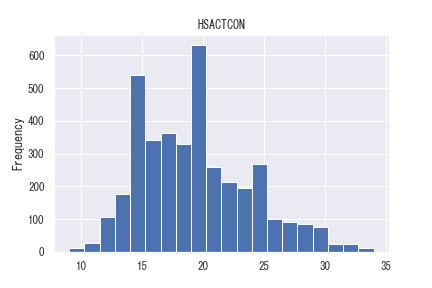
また、STAR以降の長期的な目的変数(HSACTCON: 高校時のSAT, ACTスコア)について確認します。

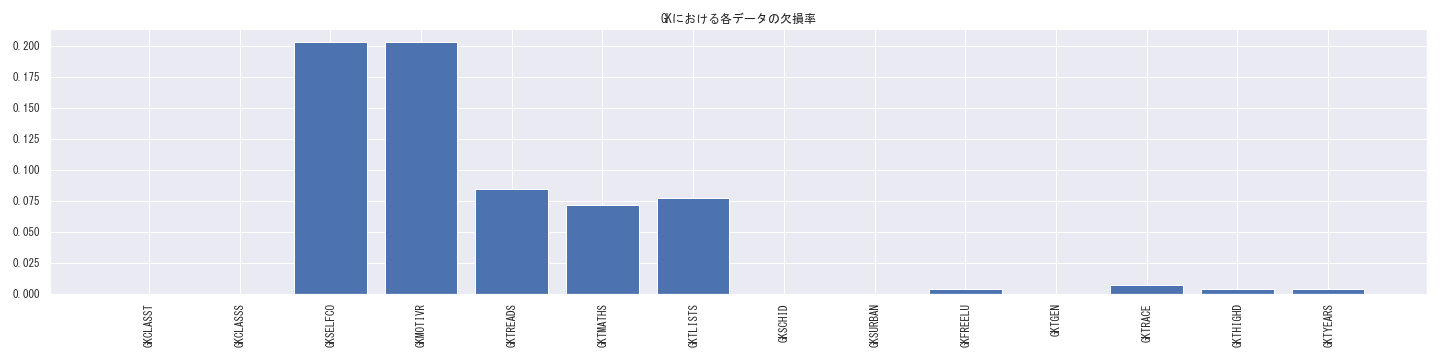
なお、データの欠損率は6割程度あります。STAR期間内の心理尺度データの欠損率が2割程度、学力テストの欠損率が7％程度だったので、高校時のデータはかなりデータ欠損率が高いことが分かります。

詳しくは記載しませんが、STARプロジェクト以降の各種変数は、年次が上がるにつれて欠損率が上がっていく傾向があります。
おそらく、STAR期間から時間経過することで、

他州への転校などにより追跡できなくなる数が増える
高校へ進学しないため、データ自体が存在しない

といった理由で、欠損が増えていったものと思われます。

ACT_SATのスコアの欠損理由を考えてみると、もし学生大学進学せず就職を希望する状況であれば、
SAT/ACTなどの学力テストを受験する必要がないため、欠損になると考えられます。
上記のような学生にSAT/ACTを受けさせた場合は、進学のための勉強などをあまり行っていないため、SAT/ACTを受験した学生よりも平均的に低い結果になることが見込まれます。
つまり、欠損値を適切に穴埋めしようと思った場合、例えば観測値の平均をそのまま割り当てる、といった処理を行うのでは、
真の値より高く見積もってしまう可能性が高いと想定されます。

このように、ランダムではなく、学生の状態に依存して欠損確率が変化すると思われる欠損値をMNAR(Missing Not At Random)と呼びます。

MNARにおけるレコードの欠損確率は、その他の変数(ここではデモグラフィック変数)と何らかの相関があるものと思われます。
例えば、(SAT/ACTのスコアと関連すると思われる)アメリカにおける高校卒業率は、フリーランチ(無料給食)の有無と負の相関があるようです。¹²

このような変数については、欠損をその他のデモグラフィック変数の値に応じた補完ロジックで予測を行うのが望ましいです。

ただ、「欠損値のないレコードのみを学習データとして、欠損値の予測モデルを構築し、予測値を使って欠損を穴埋めする」という単純な方法では「欠損が全く起こっていないデータのみで学習する」という、一種のバイアスがかかったデータで学習を行ってしまうことになり、それはそれで偏った予測を行ってしまうリスクがあります。

後述しますが、上記のようなリスクをできる限り回避するために、本記事では下記の2種類の方法で欠損データの処理・比較を行い、分析を進めていきます。

リストワイズ法(欠損データは一律削除して分析を行う)
多重代入法

（筆者がまだきちんと理解しきれていないこともあり）欠測データの取り扱いについては詳細な言及は避けますが、興味のある方がいらっしゃいましたら下記の書籍などをご確認いただくと良いかと思います。

・欠測データの統計科学
https://www.amazon.co.jp/dp/400029847X

備考

なお、本データに添付された「starUsersGuide.pdf」(英語)によると、
HSATCON(SAT, ACTのテスト結果)の欠損や算出法について、下記の記載があります。
欠損の発生理由に基づく欠損値補完ロジックを組むことで、より正しく補完できる可能性があります。

ACT, Inc.とカレッジボード、教育テストサービス（ETS）の2つのテストパブリッシャーの協力を得て、STAR の情報と ACT/SAT の受験記録を結びつけた（Krueger & Whitmore, 2001a）。2社は卒業クラスごとにファイルを整理しており、1998 年に卒業した学生は、居住地に関係なく、3 年生または 4 年生時に SAT もしくは ACT を受験していれば一致する。名前、誕生日、社会保障番号単位でファイルが一致しない STAR の学生は、試験を受けなかったと分類された。

HSACTCONはACTを受験した学生のACT合計点、SATを受験した学生のSAT合計点をACTの尺度に変換したものある。（Krueger and Whitmore, 2001aを参照）

上記で紹介してきた各目的変数について、下記にまとめます。

特徴量	取得元ファイル	列名	変数の型	備考
心理尺度(自己概念)	STAR_Students.tab	GxSELFCO	数値変数	各STAR年次ごとに個別に分析する
心理尺度(モチベーション)	STAR_Students.tab	GxMOTIVR	数値変数	各STAR年次ごとに個別に分析する
SAT学力テスト(読解力)	STAR_Students.tab	GxTREADS	数値変数	各STAR年次ごとに個別に分析する
SAT学力テスト(数学)	STAR_Students.tab	GxTMATHS	数値変数	各STAR年次ごとに個別に分析する
SAT学力テスト(リスニング)	STAR_Students.tab	GxTLISTS	数値変数	各STAR年次ごとに個別に分析する
高校時のSAT/ACTのスコア	STAR_Students.tab	HSACTCON	数値変数

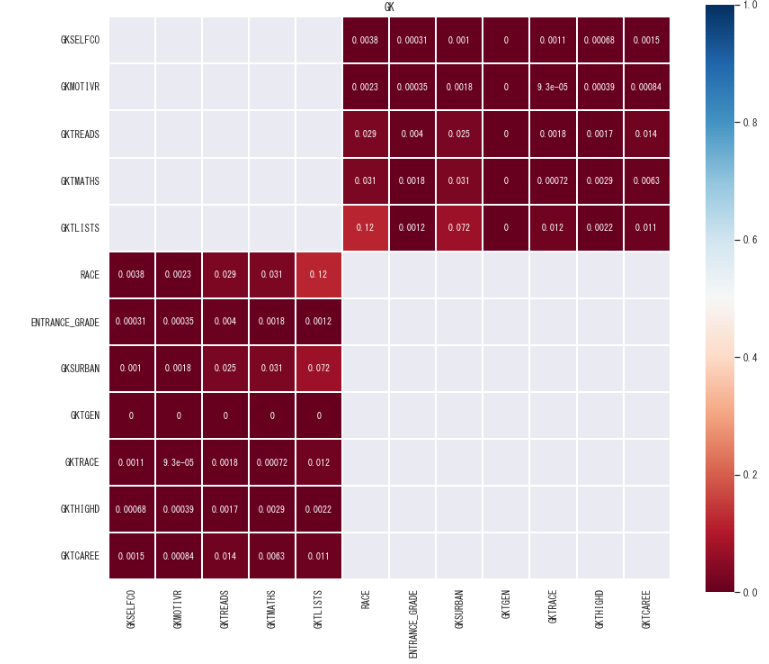
最後に、説明変数と目的変数の相関(スピアマンの相関係数)を確認していきます。
4年分のデータを確認すると冗長になるため、幼稚園時の相関係数のみ確認していきます。

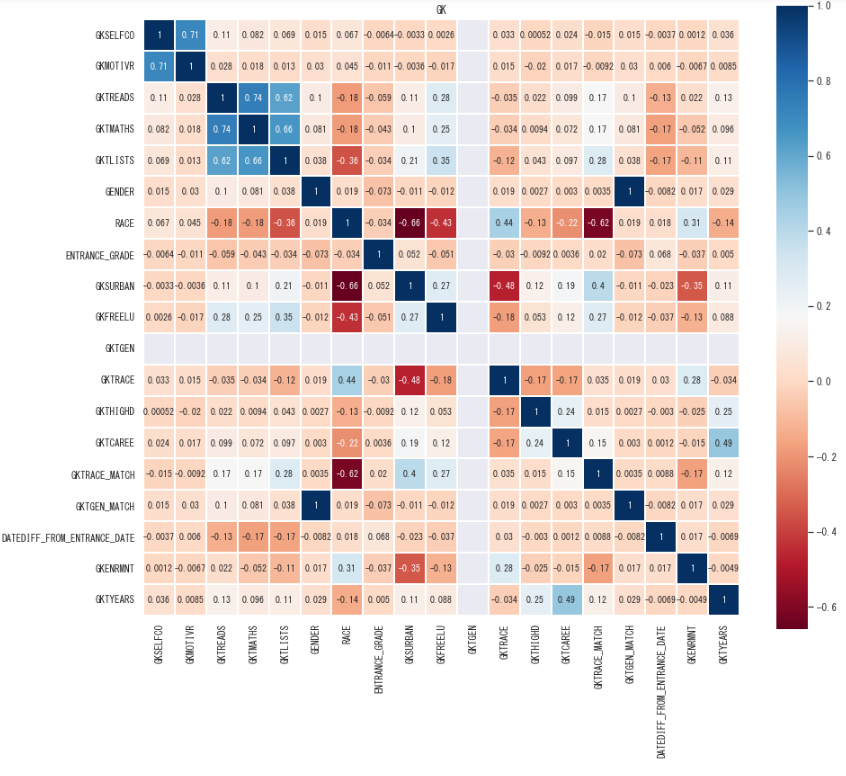
特に学力テスト回りの目的変数　(読解力テスト(GKTREADS), 数学テスト（GKTMATHS), リスニングテスト(GKTLISTS))に対して、RACE(人種)、GKFREELU(フリーランチの有無)、GKTRACE_MATCH(教師と人種が一致するかどうか)、DATEDIFF_FROM_ENTRANCE_DATE(入学日と誕生日の日数差分)間に弱い相関(±0.2~±0.4)があることが確認できます。

リスニングテストと人種の相関については、英語ネイティブの白人と、非英語ネイティブの他人種の違いに由来するという意味で、直観とも一致します。

備考

スピアマンの相関係数では(特に3値以上の値をとりうる)カテゴリ変数と量的変数間の相関関係を確認するには適切ではありません。

目的変数と、(3値以上の値をとりうる)カテゴリ変数間の相関については、別途相関比¹³行列を出力しました。

相関比ベースでみると、人種や都市の学校の都会度との相関が多少見られるようで、それ以外の相関はあまりみられません。

3. (STARプロジェクトをRCTとみなしたときの)処置効果の統計的確認

次に、処置群と対象群を比較し、処置効果(通常サイズのクラスに対して、小規模クラスが及ぼした影響量)を確認していきます。

今回の実験を元々の想定通りRCT(ランダム化比較試験)とみなす場合、実験による処置効果の平均値(ATE: Average Treatment Effect)を点推定をするのであれば、単純に2群間の平均の差(あるいは何らかのロジックにもとづいて標準化した効果量)を算出することになります。

もちろん、処置群、対象群が確率的に選ばれている以上、「偶然処置群が対象群に比べて良い結果が出てしまった」可能性も考慮する必要はあります。

上記を踏まえて、今回は下記のプロセスで処置効果の確認を行っていきます。

処置効果を表す各目的変数について、リストワイズ法・多重代入法にもとづいた欠損値の処理を行う
独立な2組(処置群・対象群)の分布が異なるかどうかを「マン・ホイットニーのU検定」によって検定する
有意差が出た目的変数について、効果量を点推定する(2群の平均の差、Cohenのd)
一定以上の効果量(Cohenのd>0.2)を持ち、かつ検定により2群間の有意差が認められた目的変数をリストアップする

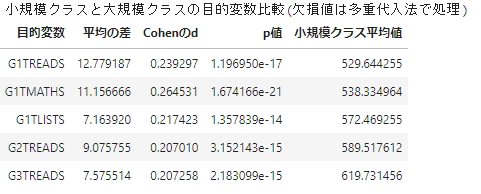
結果、

心理尺度(自己概念、モチベーション)系の特徴量は大きな差が認められなかった
SAT学力テストはいくつかの学年において(LISTS(リスニング)、MATHS(数学)、READS(読解力)一定以上の有意差が認められた
という状況が見られました。

次に、多重代入法による目的変数の欠損値の穴埋めを行った後、有意差を確認してみます。
Pythonの場合、schikit-learnのバージョン0.21以降に実装されているimpute.IterativeImputerクラスを使って多重代入法を実装することができます。

(なお、現状での実装は「experimental」となっており、ドキュメントにも記載されている通り今後のバージョンアップで実装が変わる可能性があります。)

他のscikit-learnのクラス同様、学習器は自由に渡すことができ、
fit_transformメソッドで学習から予測を行うことができます。

なお、予測器はデフォルトの実装(Bayesian Ridge回帰)で実施します。

備考

デフォルトの実装は、「係数wの事前分布を球面ガウス分布とするベイジアンリッジ回帰」となっているようです。 https://scikit-learn.org/stable/modules/linear_model.html#bayesian-ridge-regression

# テスト実装であるため、明示的に「enable_iterative_imputer」をimportすることで利用可能になる
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer

mi_list = IterativeImputer(max_iter=3).fit_transform(df['目的変数', 'その他の説明変数'])

# 全ての列について予測値が補完された多次元配列として格納されるので、必要な目的変数の予測値のみ抽出する
mi_list = [x[0] for x in mi_list]

リストワイズ法・多重代入法のいずれの欠損値処理においても、(効果量などの点推定結果は多少変わるにせよ)同様の有意差が確認できました。

備考

上記の内容を含めて、有意差の有無は個別の変数ごとにp値<0.05を閾値として確認しています。多重検定の問題を考慮していませんが、一旦大きな影響もないと考えられるため、今回はそのまますすめています。・統計的仮説検定における多重検定の問題とその対処法 https://note.com/dd_techblog/n/n8907f500b7e1

おそらく、STAR期間内の目的変数は欠損率が低く、また欠損理由自体に他の変数への依存性が低いものであったため、2つの欠損処理の間で差異が出なかったと推定されます。

次に、STAR期間後の目的変数について確認していきます。
今回利用する変数は下記です。

HSSATCON : 高校時のSAT,ACTのスコア

備考

「STAR期間中各4年間でランダムで各クラスに割り当てられている中で、4年間(4回)分のランダムな介入について、4年間を総括して「小規模クラスだったか」「通常クラスだったか」をどう分類するか」という問題を考慮する必要があります。

本データ内に、特定のロジックを元にどちらのクラスと判別したかを判定したカラム「CMPSTYPE, YEARSSMA」が存在しますので、今回はそちらを利用しました。

また、デモグラフィック変数については、全年共通ではなく、各年ごとに個別に取得したデータも存在します。（例えば、フリーランチの有無はSTAR参加年度ごとに収集しています。）

上記の場合は、「STAR期間中に取得できた変数のうち、もっとも年次が上のもの」を利用しています。

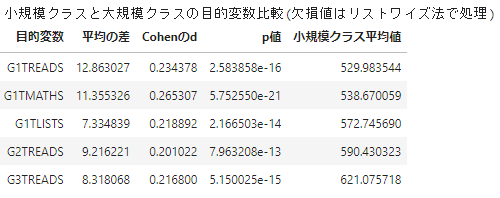
STARプロジェクト後10年後の変数であるHSSATCON(高校時のSAT_ACTのスコア)については、
欠損値を多重代入法で処理したことで2群間の差が明確になっているようです。

4. 選択バイアスの確認

次に、そもそも今回の実験がRCTかどうか（介入の割当に選択バイアスが発生していないか）を確認していきます。
選択バイアスが発生している場合、観察されたその他の説明変数についても、何らかの偏りが発生していると想定されます。

本プロジェクトにおいては、小規模クラスと大規模クラスの介入割り付けについて、
特にGENDER(性別)、RACE(人種)、FREELU(無料給食の希望有無)について、バイアスが存在しないことが検証されているようです。

一方で、上記以外のデモグラフィック変数については、介入割り付けにおいて偏りがある可能性があります。
また、単変量観点では偏りがなくても、多変量観点では偏りがあるかもしれません。

今回は、下記の方法でその偏りについて確認していきます。

介入群と対象群についてデータの可視化を行い、各変数間で分布の差異がないかを確認する
各説明変数について、多重代入法にもとづいた欠損値の処理を行う
説明変数ごとに、処置群・対象群で偏りがないかの比較(単変量での比較)
傾向スコアによる比較(多変量での比較)

データの可視化

介入群と対象群のデータを比較します。
(4年分のデータを確認すると冗長になるため、小学校1年生時の各説明変数についてのみ記載しています。)

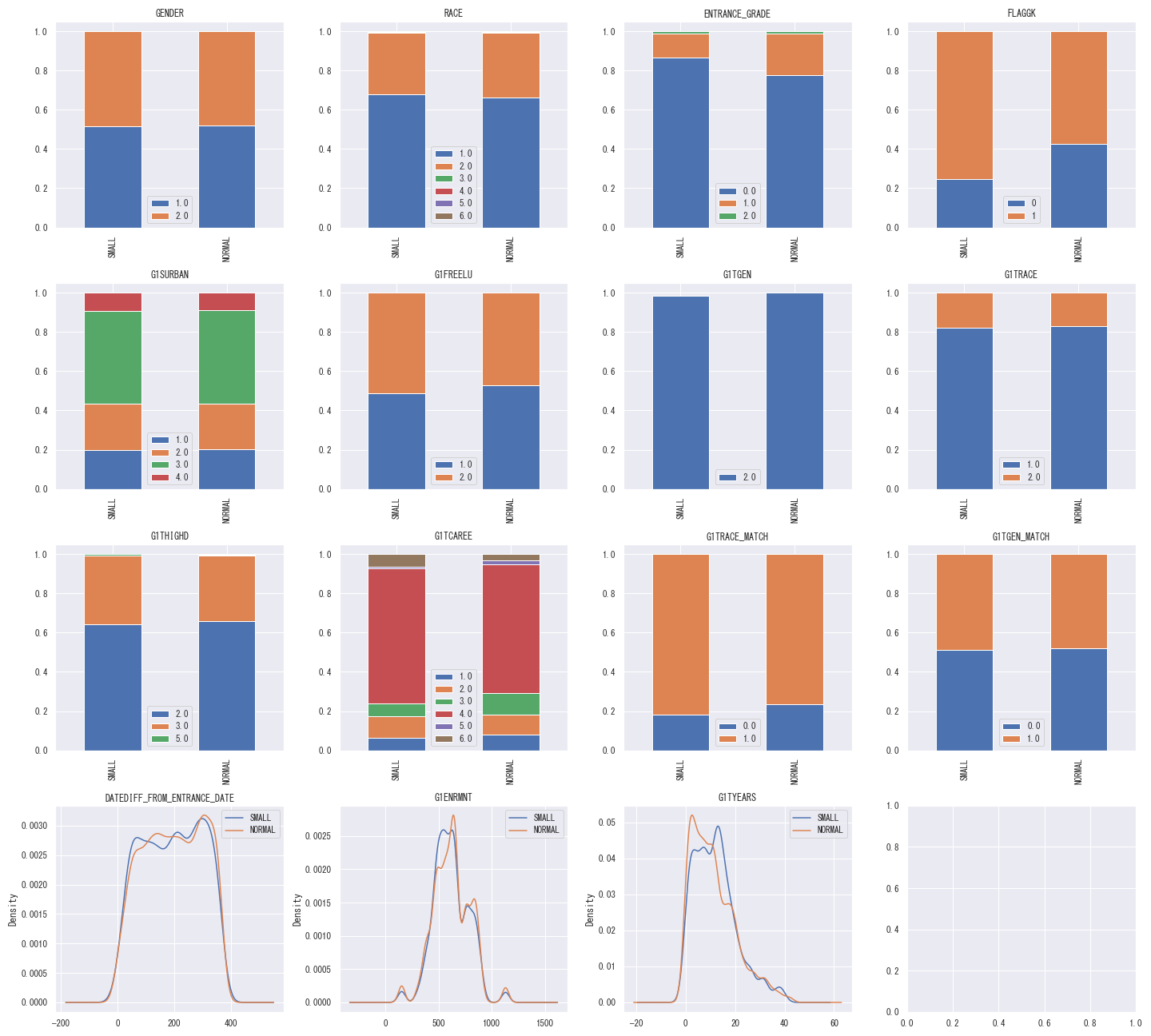
小学1年生時の分布の差について、処置群(小規模クラス)と対象群(通常クラス、通常クラス+補助員)で変数の分布を学年ごとに確認すると、
前述の通りGENDER, RACE, G1FREELUなどでは偏りはないようですが、

ENTRANCE_GRADE(入学年度)について、通常クラスのほうがAcademicRedshirting(意図的な入学年度の遅れ)が多くなっている
G1TYEARS(教師の経験年数)が通常クラスの方が高め
FLAGGK(幼稚園時のデータを利用できるか)どうかについて、小規模クラスの方が高め

といった傾向はあるようです。こういった違いが統計的に有意な差であるかは、後ほど確認していきます。

単変量での比較

処置群と対象群間の各デモグラフィック変数の分布比較は、目的変数群の2群比較とほぼ同じ手法になります。

各デモグラフィック変数について、リストワイズ法・多重代入法にもとづいた欠損値の処理を行う
独立な2組(処置群・対象群)の分布が異なるかどうかを検定する
検定により2群間の有意差が認められたデモグラフィック変数をリストアップする

備考

デモグラフィック変数にはカテゴリ変数が含まれます。
カテゴリ変数では2群間の分布比較の際の検定手法、効果量の測定手法が量的変数と異なります。

今回は、下記の手法で分布の差を確認します。

量的変数(目的変数の時と同じ)
　検定: マン・ホイットニーのU検定
　差の大きさ: 2群の平均の差、Cohenのd
カテゴリ変数
　検定: カイ二乗検定
　差の大きさ: クラメールの連関係数/b>

デモグラフィック変数についてカテゴリ変数と数値変数それぞれについて有意差を確認すると、

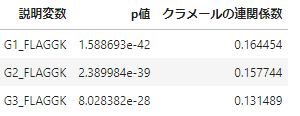
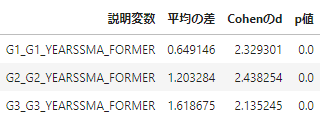
幼稚園時のデータが使えるかどうか(FLAGGK)や、過去のSTARプロジェクト参加年度における小規模クラス経験回数(YEARSSMA_FORMER)で一定以上の有意差が発生しました。

実験当時のテネシー州では小学校に入るのは義務教育であるものの、幼稚園に入るかどうかは選択制であったようで³、
小学1年生以降の実験において、小規模クラスへの割り当てについて、幼稚園に行った（≒幼稚園時のデータが使える）学生が割り当てられやすくなる傾向が出ています。
推測になりますが、中途学年から新しくSTARプロジェクトに参加した学生の群割り当てについて、プロジェクト遂行上何らかの制約があったのかもしれません。

多変量での比較

今まででは、単変量ごとに2群間比較を行い、群間に差があるかの統計検定、効果量の測定を行ってきました。
ここでは、多変量のデモグラフィック変数について、「傾向スコア」を使って2群間の比較を行っていきます。
傾向スコアとは、共変量を元に「処置群」に割り当てられる確率を計算したものです。確率算出には、通常ロジスティック回帰が使われることが多いようです。

備考

傾向スコアはあくまで確率を予測したものであるため、ロジスティック回帰以外にも機械学習で使われるアルゴリズムを利用することが可能です。
なお、傾向スコアを用いた因果推論を行う際には、データにおいて「SUTVA」等の前提を満たす必要があります。¹⁴ 本来前提を満たすかどうかの確認は簡単ではありませんが、今回は一旦これらの前提が満たされているものとして解析をすすめています。

欠損値の処理→傾向スコアの算出を行います。
下記は、学年ごとの全レコードについて、デモグラフィック変数のみを使って
傾向スコア（処置群(小規模クラス)への割り当て確率）を計算し、その分布を確認したものです。

分布を確認すると、幼稚園時はある程度ランダム性が高いと思われるものの、
小学校1年生～小学校3年生は、大きく2つの山があり、明確に傾向に違いがあるようです。

小学校1年生～小学校3年生までの傾向スコア分布の2峰で、説明変数群の分布の差を確認すると、
・特に「幼稚園時にSTARプロジェクトに参画していたか(FLAGGK)」「過去のSTAR参加年度数」
・入学年度(ENTRANCE_GRADE)
説明変数における2群比較時と同様、大きな差が見受けられました。

5. 傾向スコアによる補正等を行った際の介入効果の確認

最後に、上記の傾向スコアを用いて、介入効果の補正を行った上で、処置群と対象群の目的変数の比較を行っていきます。

今回はIPW（逆数重みづけ）法を用いた手法を実施します。
やり方は簡単で、処置群と対象群の各目的変数を、処置群に割り当てられる確率(傾向スコア)について、確率が高いほど重みを軽く、確率が低いほど重みを重くすることで、
バイアスの効果を取り除いて処置効果の比較を行うことができます。

このように算出したIPW推定量には不偏性があり、バイアスのある2群の比較において(ある程度)妥当な推定を行うことができます。

IPWのアルゴリズムの詳細や、問題点などについては、下記の書籍が詳しいかと思いますので、ご参考にしていただければ幸いです。

・調査観察データの統計科学(第３章　セミパラメトリック解析)
https://www.iwanami.co.jp/book/b257892.html

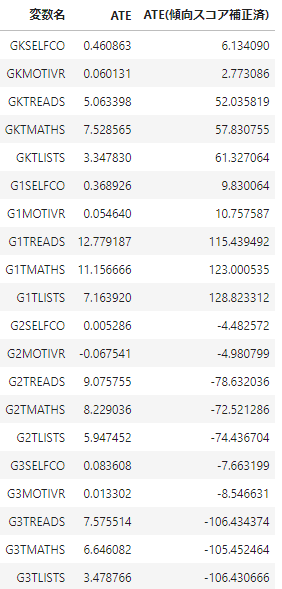
早速上記について、ATEのIPW補正値を推定した結果を下記に記載します。

全体として、

幼稚園、1年生時の結果については傾向スコアの補正により、より処置効果が大きくなった
2年生、3年生時の結果については逆に処置効果が小さくなり、ものによっては介入によってマイナスの影響を与えると解釈されるようになった

様子が確認できました。

6. まとめ

今回、STARプロジェクトという大規模なプロジェクトについて、統計検定、因果推論という2つの手法を用いて検証を行ってみました。
STARプロジェクトのデータについては日本語でまとまった資料がないため、データの確認には苦労できましたが、
「教育における最大規模のRCT」ということからデータも充実しており、今後も色々と分析を進めてみようと思います。

今回はあくまでRCTかどうか、処置効果の平均(ATE)を元に確認していきましたが、
実際の分析現場では「特定の属性を与えられた時の処置効果の平均(CATE)」（この例であれば、処置効果は男性と女性で異なるか、人種ごとに異なるか、など）が重要になってくることも多いかと思います。

引き続き、本データセットを使って、最新の機械学習アルゴリズムとライブラリ(EconML)を用いたCATEの分析などを進めていければと思います。

ありがとうございました。

アメリカにおける教職員配置の改革動向
https://www.jstage.jst.go.jp/article/kansaisea/28/0/28_48/_pdf/-char/ja ↩
今後の学級編制及び教職員定数の改善に関する有識者ヒアリング
https://www.mext.go.jp/b_menu/shingi/chousa/shotou/072/shiryo/attach/1293877.htm ↩
Some findings from an independent investigation of the Tennessee STAR experiment and from other investigations of class size effects.
https://journals.sagepub.com/doi/10.3102/01623737021002143 ↩ ↩² ↩³
The Effects of Academic Redshirting and Relative Age on Student Achievement
https://eric.ed.gov/?id=EJ973826 ↩
Is Early Learning Really More Productive? The Effect of School Starting Age on School and Labor Market Performance
https://www.researchgate.net/publication/5095819_Is_Early_Learning_Really_More_Productive_The_Effect_of_School_Starting_Age_on_School_and_Labor_Market_Performance ↩
Kindergarten Entrance Ages: A 35 Year Trend Analysis
http://www.ecs.org/clearinghouse/73/67/7367.pdf ↩
Same-sex and opposite-sex teacher model influences on science career commitment among high school students.
https://psycnet.apa.org/record/1979-09651-001 ↩
Unmasking the Myth of the Same-Sex Teacher Advantage
https://www.researchgate.net/publication/233388680_Unmasking_the_Myth_of_the_Same-Sex_Teacher_Advantage ↩
The Long-Run Impacts of Same-Race Teachers
https://www.aeaweb.org/articles?id=10.1257/pol.20190573
※STARプロジェクトのデータを使った研究 ↩
Do teachers’ years of experience make a difference in the quality of teaching?
https://www.sciencedirect.com/science/article/pii/S0742051X20313810 ↩
What Does Certification Tell Us About Teacher Effectiveness? Evidence from New York City
https://www.nber.org/papers/w12155 ↩
Diploma Disparities: High School Graduation Rates in New York City
https://comptroller.nyc.gov/reports/diploma-disparities-high-school-graduation-rates-in-new-york-city/ ↩
相関比(１/２）株式会社アイスタット｜統計分析研究所
https://istat.co.jp/sk_commentary/correlation_ratio ↩
傾向スコアを用いた共変量調整による因果効果の推定と臨床医学・疫学・薬学・公衆衛生分野での応用について
https://www.niph.go.jp/journal/data/55-3/200655030007.pdf ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up