制御バリア関数(CBF)を使えるようになろう

はじめに

制御界隈では言わずと知れた制御バリア関数(CBF: Control Barrier Function)。ロボットが安全な「状態」から逸脱しないように数理的制約を課し、最適化によって入力を決める制御方法の一種ですが、あまりダイレクトに解説してくれている日本語の記事を見かけません。

※元論文はこちら
Control Barrier Functions: Theory and Applications

この記事では、制御に関する前提知識がほとんど無い人でも吐き気を催さずに制御バリア関数を理解できるよう、難しい数式はなるべく省いた説明を心掛けます。ただし、高校物理&数Ⅲまでの数学は理解している人が対象です。また議論が厳密でない部分は多々あると思いますが、ご了承ください。

とりあえず安全制約を考えよう

問題設定

直線上を動くロボットがあるとします。今あなたはこのロボットに速度指令を出すことが出来ますが、$x=1$のところに立ち入り禁止の看板があり、それより先に進むとロボットは落下してしまいます。

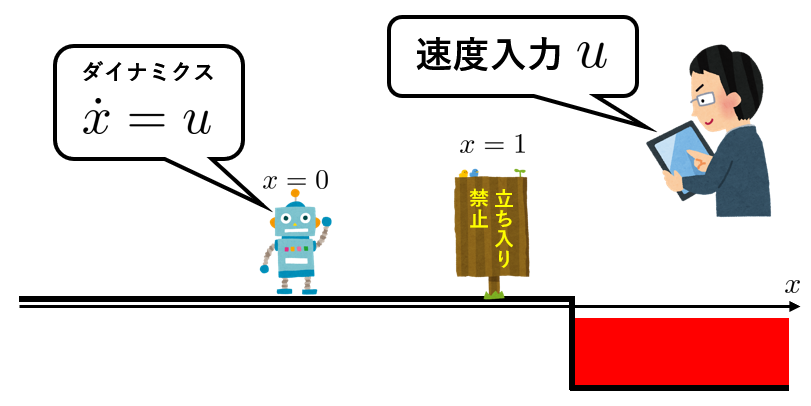
人間の操作は絶対安全とは限りません。うっかりロボットが落ちてしまわないよう、タブレットに安全機能を設けましょう。
まず初めに思いつくような安全機能は次のようなものではないでしょうか。

• 安全機能は人間の入力$u$を審査し、(必要に応じて編集した上で)ロボットに実際の指令$u'$を伝える。
• ロボットの位置$x$が$x> 1$の時は、$u<-1$ならば$u'=u$、$u\geq -1$ならば$u'=-1$
• ロボットの位置$x$が$x=1$の時は、$u<0$ならば$u'=u$、$u\geq 0$ならば$u'=0$
• ロボットの位置$x$が$x<1$の時は、$u'=u$

すなわち、ロボットが安全地帯にいる時は人間の信号を素通ししますが、ロボットが危険地帯に入った時は強制的に引き戻す、あるいは負の方向の速度入力のみ受け付ける、という安全装置です。勿論これはとても妥当な安全対策です。でも条件分岐のオンパレード。if文でプログラミングするのは骨が折れますね...。

もう少し場合分けせずに$u'$を決める方法はないでしょうか。

最適化問題

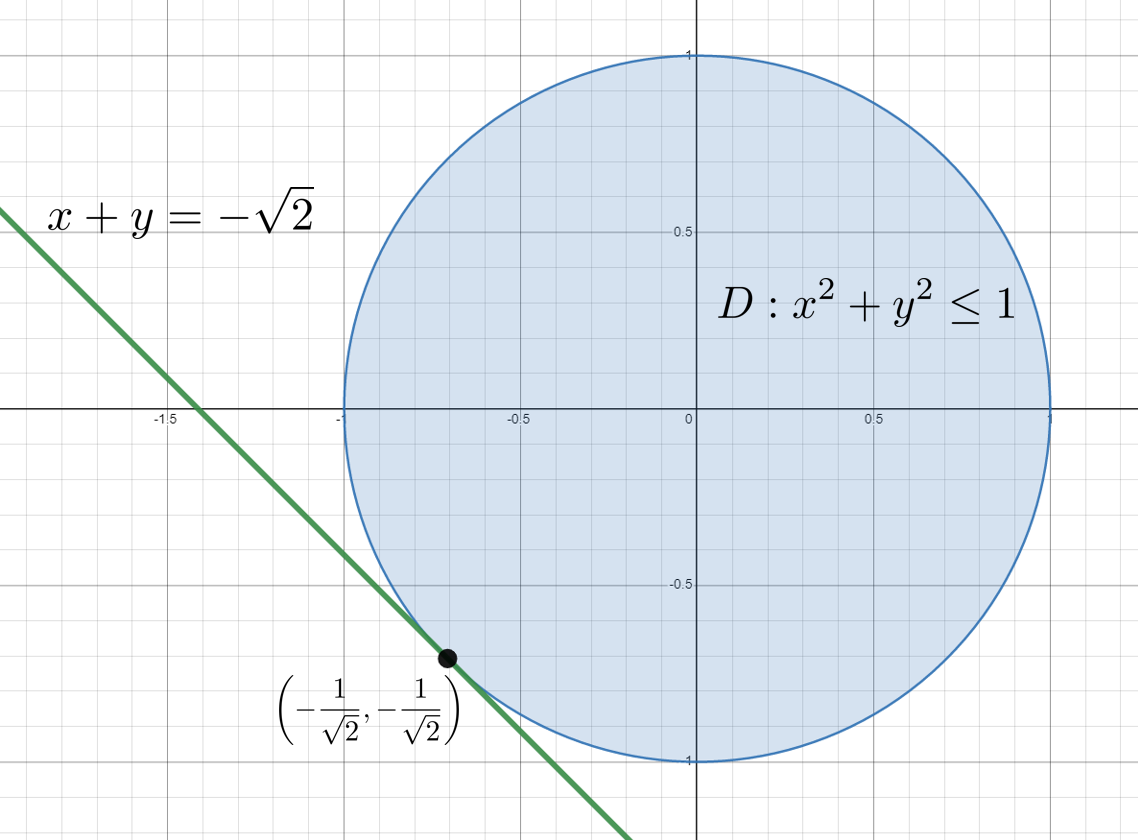
ここで少し高校数学に戻ってみましょう。次のような問題を解いたことはあるでしょうか。

問
$x^2+y^2\leq1$で表される領域を$D$とする。$D$内の点$(x,y)$のうち、$x+y$の値を最小化する点を答えよ。
解
$x+y=k$とおくと、この式は$xy$平面内の直線を表す。この直線と$D$が共有点を持つという条件の下で$k$の値を小さくしていくと、点$(-1/\sqrt2,-1/\sqrt2)$において$k_{min}=-\sqrt2$であることがわかる。よって$(-1/\sqrt2,-1/\sqrt2)$が解である。

この問題をもう少しすっきり書くと、

minimize\, \,\,\, x+y\\
s.t.\,\,\, x^2+y^2\leq 1

となります。$x^2+y^2\leq 1$のもとで(such that)、$x+y$を最小化(minimize)せよ、ということですね。専門用語では、この$x+y$を評価関数(あるいはコスト関数)、$x^2+y^2\leq 1$を拘束(あるいは制約)条件といいます。そして、評価関数を拘束条件のもとで最小化する問題を、最適化問題というのです。最適化問題を解くためのプログラムは世の中に沢山転がっています。今回は、その解き方は一度置いておいて、安全制約を最適化問題に落とし込む方法を考えてみます。

安全制約を最適化問題にする

先程の問題設定で考えた、安全機能をもう一度確認します。

• 安全機能は人間の入力$u$を審査し、(必要に応じて編集した上で)ロボットに実際の指令$u'$を伝える。
• ロボットの位置$x$が$x> 1$の時は、$u<-1$ならば$u'=u$、$u\geq -1$ならば$u'=-1$
• ロボットの位置$x$が$x=1$の時は、$u<0$ならば$u'=u$、$u\geq 0$ならば$u'=0$
• ロボットの位置$x$が$x<1$の時は、$u'=u$

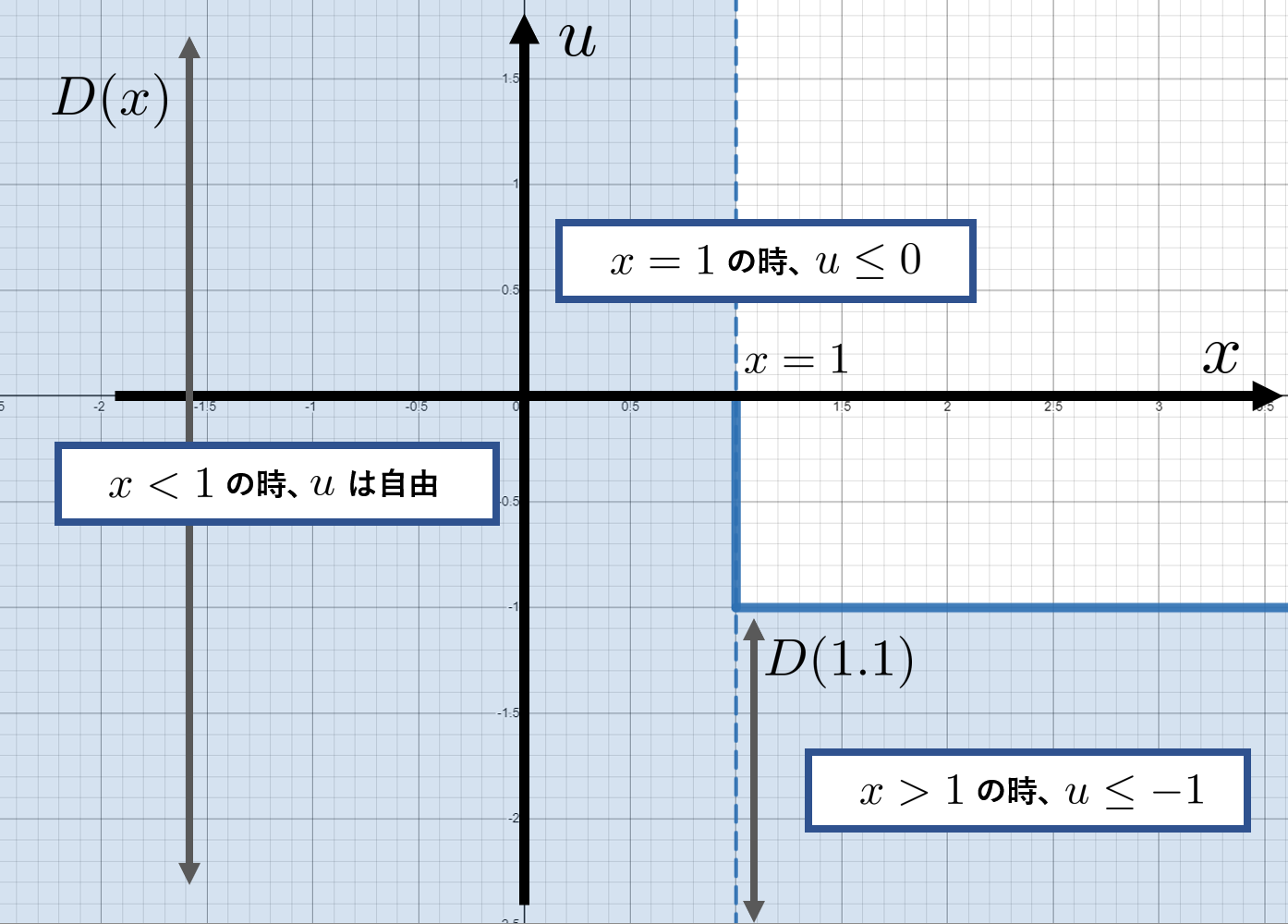
この問題の解$u'$は、次の最適化問題と同じになるはずです。

minimize\, \,\,\, |u'-u|\\
s.t.\,\,\, u'\in D(x)\\
D(x)=\left\{
\begin{aligned}
&-\infty<u'<\infty\,\,\,(x<1)\\
&-\infty<u'\leq 0\,\,\,(x=1)\\
&-\infty<u'\leq -1\,\,\,(x>1)\\
\end{aligned}
\right.

この問題は1次元の最適化です。$u'$が存在できる範囲$D(x)$が自機位置$x$の関数になっています。$u'$が$D(x)$内に存在するという拘束条件の下で、評価関数$|u'-u|$($u'$と$u$の差の大きさ)をなるべく小さくしなさい、という問題ですね。これで安全が保障され、かつ人間の入力$u$になるべく近い$u'$が求まることになります。
例えば$x=1.1$という危険域に足を踏み込んでいる場合は、$u=10$のように人が正方向に速度を入れていても、$u'\in D(1.1)$より$u'\leq -1$が指定されるので$u$に最も近い$u'=-1$が解になるわけです。

関数で領域と制約を再定義する

安全領域を関数h(x)で表す

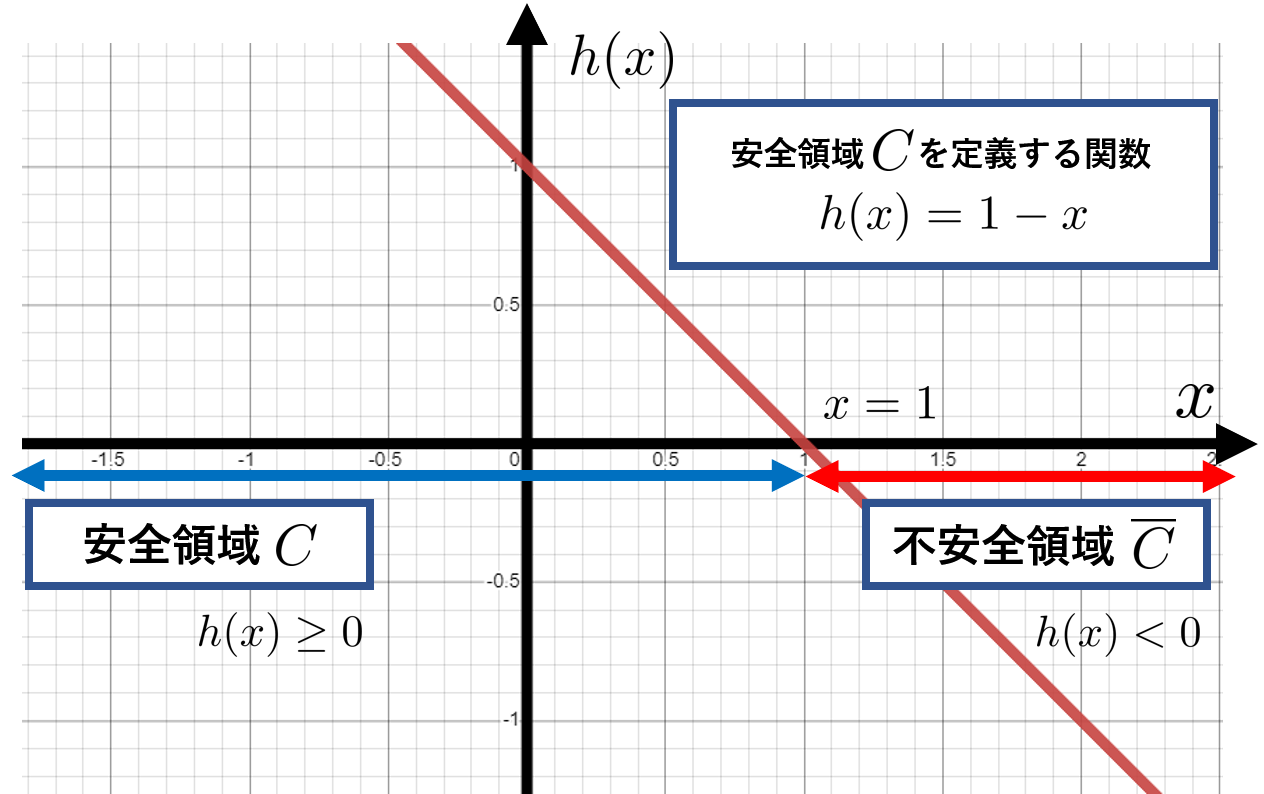
さて、ここまでで安全制約を最適化問題として解くアイデアを紹介しました。しかしまだ$D(x)$の場合分けが煩雑です。そこで新たに安全領域を関数で表す、というアイデアを紹介します。
冒頭の問題では、$x=1$を踏み超えてはならないという問題を考えていました。ここで、$x$がいてよい領域、すなわち安全領域$C$を、$C=\{x\mid h(x)\geq 0\}$のように関数$h(x)$を用いて定義します。本問では、$h(x)=1-x$とすればよいです。(他にも様々な$h(x)$が考えられますが、今はこれを使いましょう。)

安全機能を関数h(x)で表す

ロボットが安全で居続けるということは、$h(x)\geq 0$が成り立ち続けるということと同値です。$x$は時間によって変化しますので、$h(x)$も暗に時間の関数です。そこで、速度$\dot x(=dx/dt)$を考えるため、$h(x)$を時間で微分してみましょう(合成関数の微分(数Ⅲ)を使います)。

\begin{aligned}
\dot{h}(x)&=\frac{dh(x)}{dx}\times\frac{dx}{dt}\\
&=(1-x)'\times \dot x\\
&=-u
\end{aligned}

なかなか綺麗な式が出てきました。ここで一度高校2年生に戻って、次の太郎くんと花子さんの会話を聞いてみましょう。

連続で微分可能な関数$f(x)$は$f(0)=0$である。$x\geq 0$で常に$f(x)\geq 0$であるためには、$f'(x)$はどのような条件を満たせばよいか考えよ。

太郎「簡単だよ、$f'(x)\geq 0$であればいいさ。」
花子「あら、どうして？」
太郎「$f'(x)\geq 0$なら、$f(x)$が減少することはない。$f(0)=0$なんだから、これ以上$f(x)$が減少しなければ$f(x)\geq 0$が成り立つだろう？」
花子「それは十分条件ね。でも逆は成り立たないわよ。$f(x)=\sin^2x$とか、$f'(x)$が負になるときもあるけど、$f(x)\geq 0$でしょう？」
太郎「ぐぬぬ」

この問題、ふざけているようで制御では昔結構問題になっていました。冒頭の問題に当てはめると、$h(x)$は暗に時間の関数ですから、$h(x)\geq 0$であるために、$h(x)$は時間経過で減少してはならない。すなわち$\dot{h}(x)=-u\geq 0$でなければならない。よって$u\leq 0$という入力しか許してはならない。という結論になります。これではロボットがどこにいようと正の速度入力が出来ないことになり、たしかに絶対安全ですが、保守的すぎて困ります。

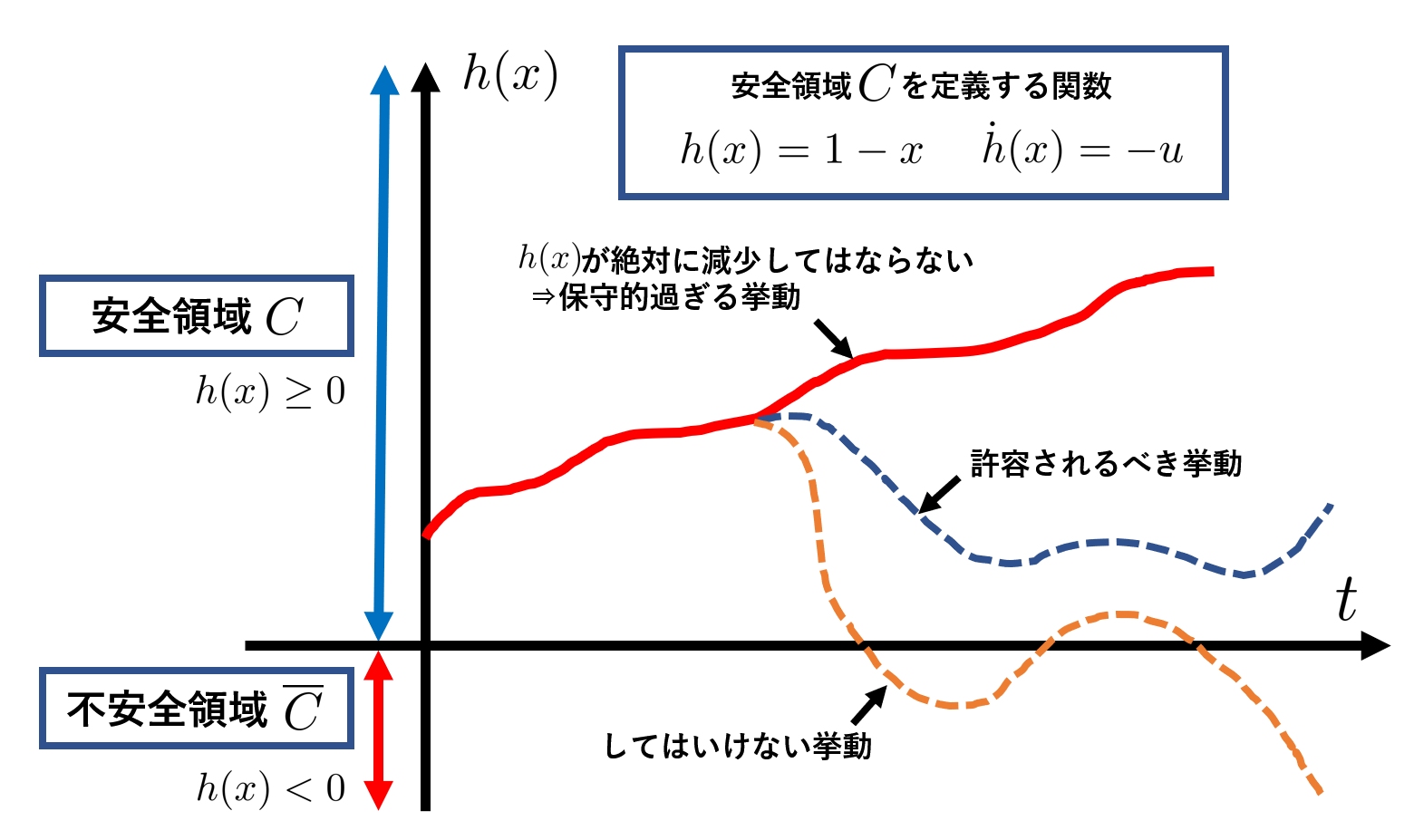
太郎くんと花子さんの会話の続きを見てみましょう。

花子「ぶっちゃけ$f(x)>0$の時って、$f(x)$は減っても増えてもいいから$f'(x)$の条件は定まらないわよね。」
太郎「確かに。$f(x)=0$の時に、$f'(x)\geq 0$でさえあれば大丈夫ってことか。」
花子「そういうこと。それが必要条件ね。」

この考察を冒頭の問題に当てはめて得られる結果は、「$x=1$の時には、$-u\geq 0$、すなわち$u\leq 0$であれ。」これは一番最初の安全機能とほぼ一致します。しかしここから応用が利くのが$h(x)$の良いところです。追加の要求として、次の2つを考えましょう。

• 不安全領域に入ってしまった場合、必ず安全領域に引き戻すような制約をつけたい。
• たとえ安全領域にいても、不安全領域との境界付近では、安全領域を飛び出していくような方向の極端に大きな入力は許したくない。

太郎くんと花子さんの会話はあくまで数学の話ですが、制御は物理システムが相手です。これらは極めて妥当な要求でしょう。そしてこれらは数式で次のように解釈されます。

• $h(x)<0$では$\dot{h}(x)>0$であって欲しい。
• $h(x)>0$でも、$h(x)=0$の近傍では$\dot{h}(x)$はある程度大きくあって欲しい。

さあ、制約の全体像が見えてきました。$h(x)$と$\dot{h}(x)$に対して、次のような図が成り立っていると望ましいということになります。

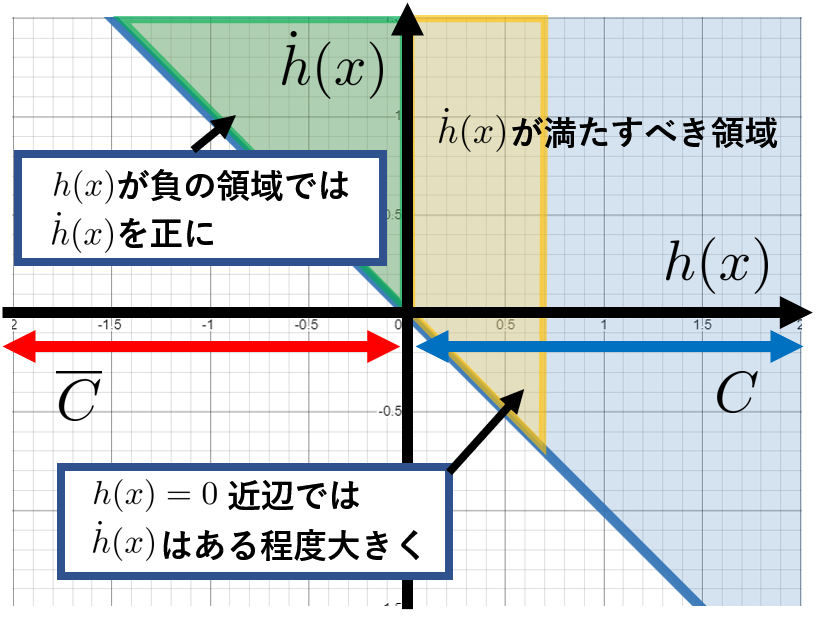
すなわち、$h(x)$と$\dot{h}(x)$の関係式の一例として、

\dot{h}(x)\geq -h(x)

「のような大小関係」が求められるということです(詳しくは次章)。
もとの問題設定では、$h(x)=1-x$、$\dot{h}(x)=-u$でした。

\begin{aligned}
-u&\geq -(1-x)\\
\iff u&\leq 1-x
\end{aligned}

改めて上のグラフを$x$、$u$を軸として描くと次のようになります。

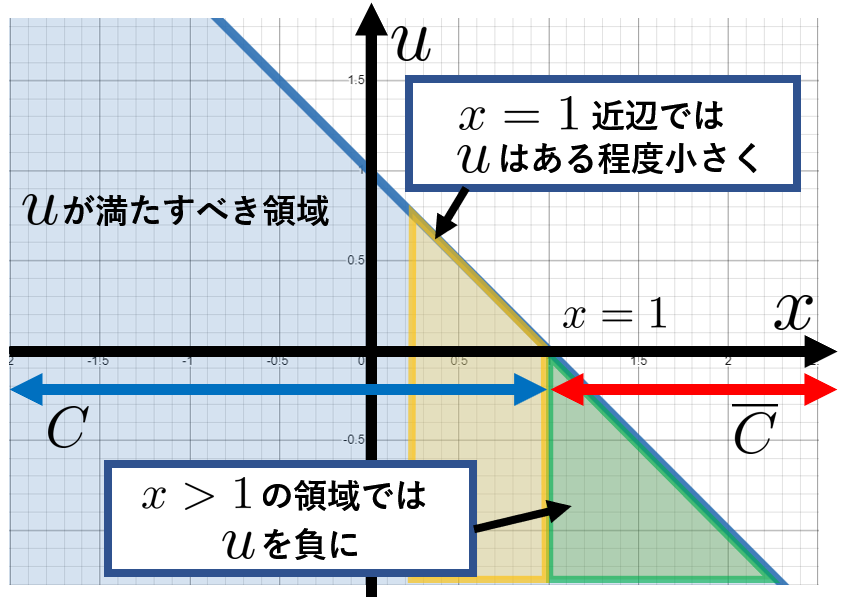
最後にこれを最適化問題として書き直してみます。

minimize\, \,\,\, |u'-u|\\
s.t.\,\,\, u'\leq 1-x

1章の$D(x)$を使った最適化問題から一転、場合分けが無くなってとてもすっきりした問題になりました。拘束条件を前章のものと見比べてみましょう。

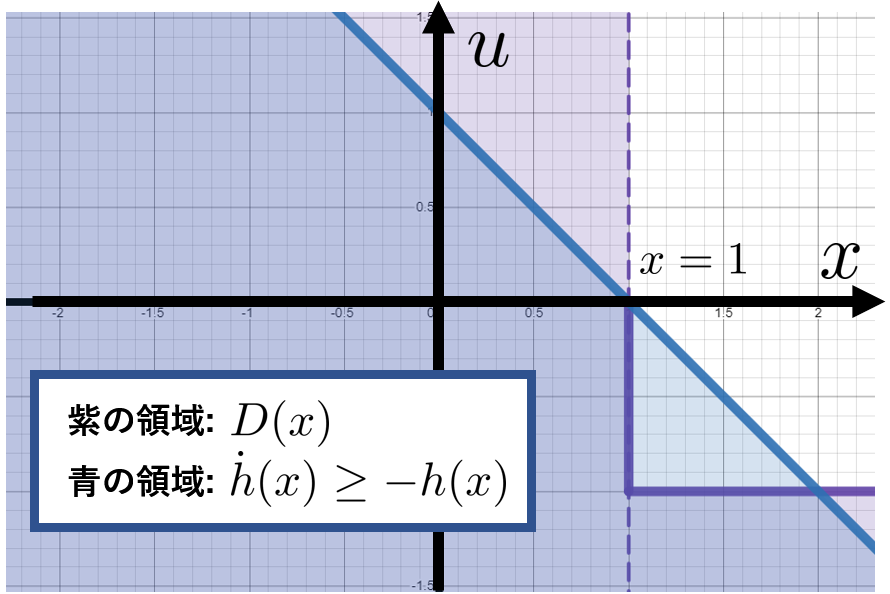
見た目は違いますが、$x=1$を境に正負が分かれるなど、要所に共通点も見られます。
$\dot{h}(x)<-h(x)$の方が滑らかな制御が可能な一方、良くも悪くも安全領域境界付近での操作性は悪くなっています。

制御バリア関数

拡張クラスΚ関数

さて、先ほど

$h(x)$と$\dot{h}(x)$の関係式の一例として、

\dot{h}(x)\geq -h(x)

「のような大小関係」が求められる

と述べました。ですが、$\dot{h}(x)\geq -2h(x)$ではいけない理由は見当たりません。もう一度$h(x)$と$\dot{h}(x)$の関係について、満たすべき要求を整理しましょう。

• $h(x)<0$の時、$\dot{h}(x)>0$。(不安全領域からは引き戻す必要がある。)
• $h(x)=0$の時、$\dot{h}(x)\geq 0$。(それ以上不安全領域に近づいてはならない。)
• $h(x)>0$の時、$h(x)$が大きいほど$\dot{h}(x)$は自由に動いてよい。(十分に安全な領域では自由に制御したい)

するとこれらを満たす$h(x)$と$\dot{h}(x)$関係は、次のようなグラフになると理想的です。つまり、前章の$\dot{h}(x)\geq -h(x)$は条件の一例に過ぎません。

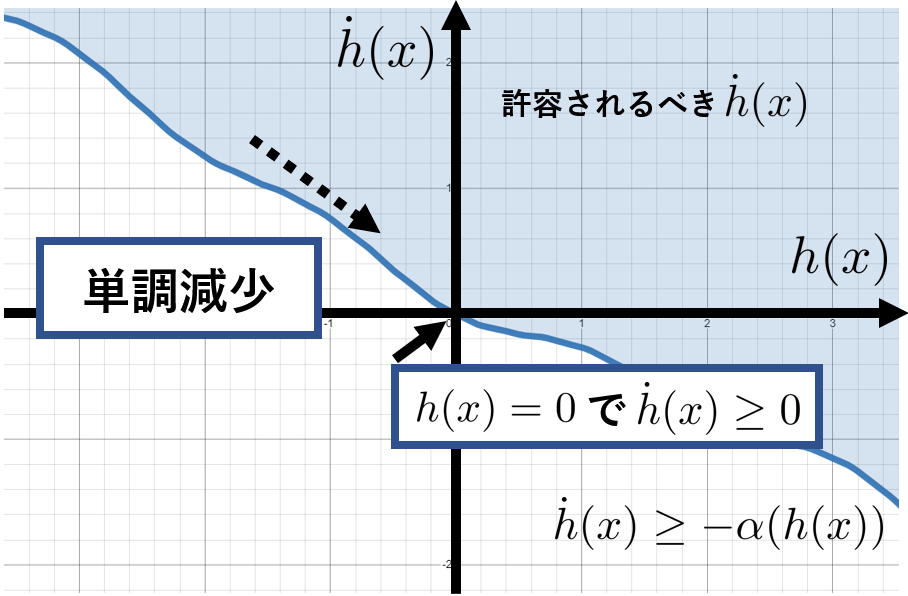
この$\dot{h}(x)$の下限を決める境界となる関数を$-\alpha(h(x))$としましょう。すると$h(x)$と$\dot{h}(x)$関係は

\dot{h}(x)\geq -\alpha(h(x))

でさえあればよい、ということになります。ただし、$-\alpha(h)$は連続で(厳密に)単調減少し、$-\alpha(0)=0$を満たす関数。すなわち$\alpha(h)$は連続で(厳密に)単調増加し、かつ$\alpha(0)=0$を満たす関数です。このような関数$\alpha(h)$は専門用語で拡張クラスΚ関数とも呼ばれています。

定式化

さて、これで安全領域$C$に対応する安全制約が$\dot{h}(x)\geq -\alpha(h(x))$という不等式で表せることが分かりました。ここからざっくりと、次の定理が成り立ちます。

[制御バリア関数を用いた安全保障]

$\dot x=f(x,u)$というダイナミクスで動くシステムに対し、スカラ関数$h(x)$と、$C=\{x\mid h(x)\geq 0\}$で定義される安全集合$C$を定義する。この時、入力$u$が$\dot{h}(x)\geq -\alpha(h(x))$を満たし続けるならば、$C$内から動き始めたシステムは$C$内に留まり続け、$C$外から動き始めたシステムもいずれ$C$内に留まり続ける。

また、人間の入力$u$に対し、可能な限り$u$に近く、かつシステムの安全を保障する入力$u'$を求めるには、次の最適化問題を解けばよい。

minimize\, \,\,\, |u'-u|\\
s.t.\,\,\, \dot{h}(x)\geq -\alpha(h(x))

なお、拘束条件の式に$u'$が出てきていませんが、問題ありません。

\begin{aligned}
\dot{h}(x)&=\frac{dh(x)}{dx}\times\frac{dx}{dt}\\
&=\frac{dh(x)}{dx}\times f(x,u')\\
\end{aligned}

なので、拘束条件の式は暗に$u'$を含んでいます。さあ、ここまで引っ張り続けてきましたが、この$h(x)$こそ制御バリア関数と呼ばれるものの正体です。

制御バリア関数(応用編)

α、hはなんでもいいのか？

さて、ここからはさらに細かい議論をしていきます。まずは制御バリア関数$h(x)$や拡張クラスΚ関数$\alpha(h)$は、式によって動特性にどう影響するのかを考えてみましょう。はじめに、冒頭の問題を例に$u$の制約を表すグラフと動特性を定性的に紐づけて理解しておきましょう。次のグラフを見てください。

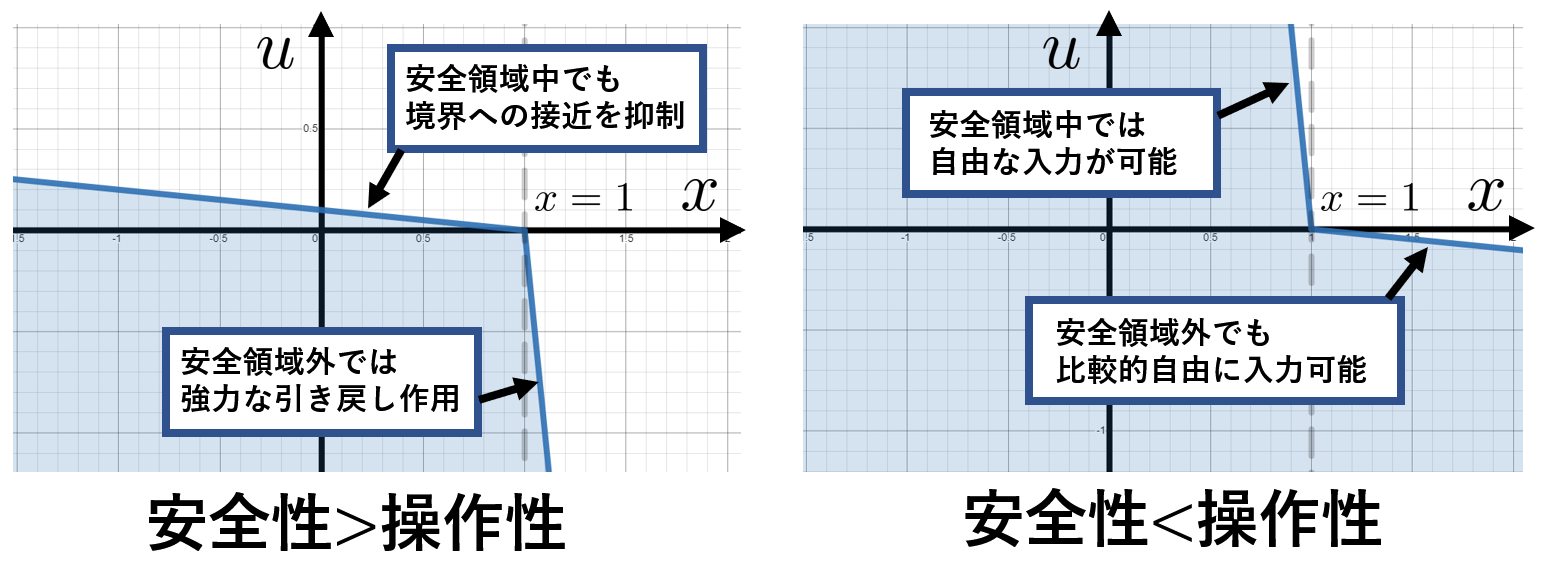
左側は、$u$の制約が厳しい例です。ロボットが安全領域内にいる時も大きな正方向の入力が出来ず、境界に近づくのが難しくなっています。また安全領域外ではたちまち大きな負の方向の入力が要求されるため、安全領域内に帰るような強い引き戻しが生じます。したがって、操作性よりも安全性を重視した制約と言えるでしょう。一方右側は、$u$の制約が緩い例です。安全領域内では境界に近くても自由に正方向の入力が可能です。また安全領域外であっても少しでも戻る方向の入力であれば許容されます。したがって、こちらは安全性よりも操作性を重視した制約と言えるでしょう。

さて、まずは制御バリア関数$h(x)$の比較を行います。冒頭の問題では$x\leq 1$が安全領域であり、これを定義するために$h(x)=1-x$としました。ですが他の関数でも同じ安全領域が定義できるはずです。

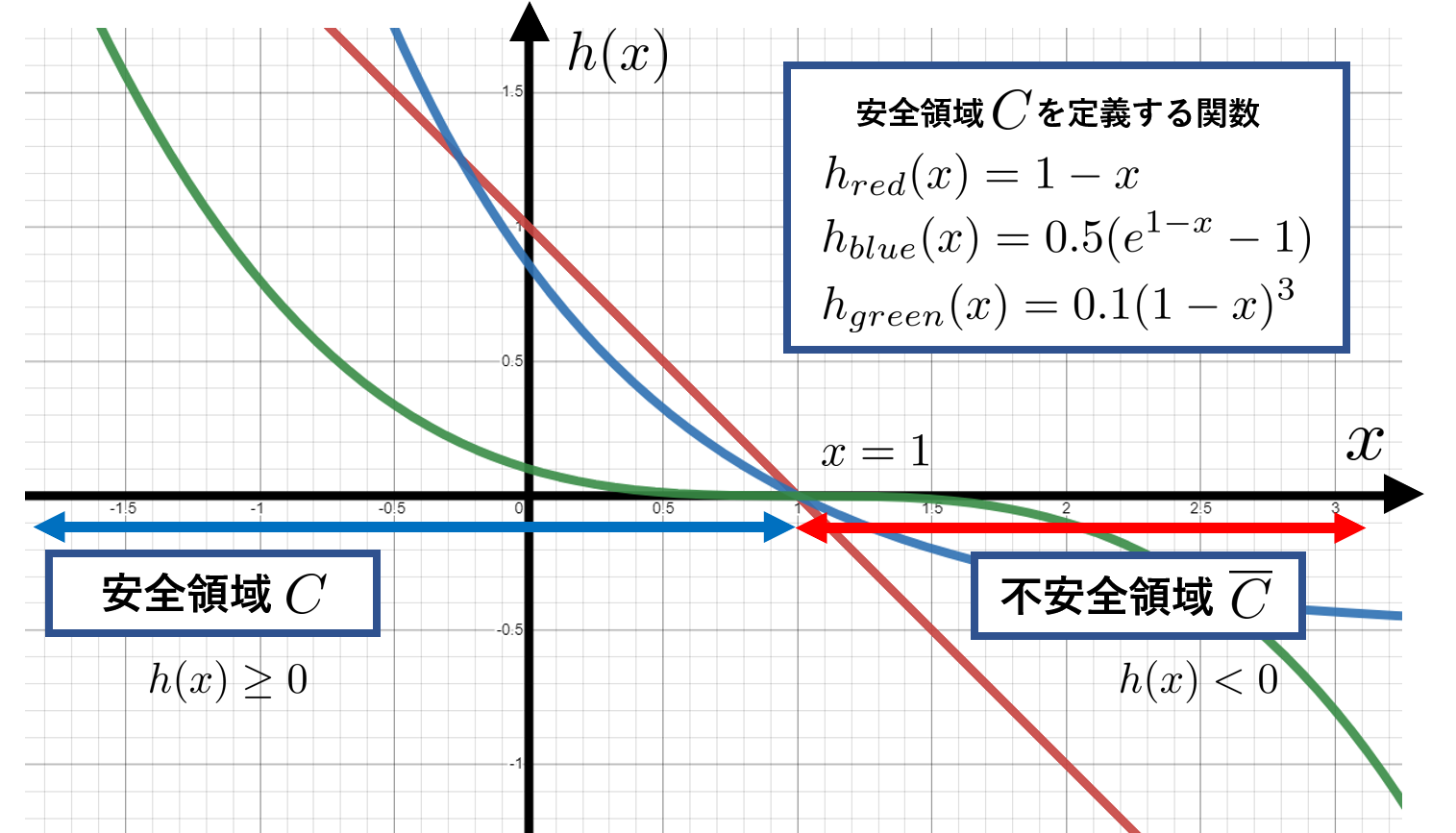
ここでは、上の3つの制御バリア関数それぞれに対し$u$の制約を考えてみましょう。公平に比較するため、$\alpha(h)=h$に統一します。$u$の制約はそれぞれ次のようになります。
$h_{red}(x)$に対する制約:

\begin{aligned}
\dot h_{red}(x)=-u&\geq-(1-x)\\
\iff u&\leq 1-x
\end{aligned}

$h_{blue}(x)$に対する制約:

\begin{aligned}
\dot h_{blue}(x)=0.5(-e^{1-x})u&\geq-(0.5(e^{1-x}-1))\\
\iff e^{1-x}u&\leq e^{1-x}-1\\
\iff u&\leq 1-e^{x-1}
\end{aligned}

$h_{green}(x)$に対する制約:

\begin{aligned}
\dot h_{green}(x)=-0.3&(1-x)^2u\geq-0.1(1-x)^3\\
\iff &(1-x)^2u\leq\frac{1}{3}(1-x)^3\\
\iff &\left\{
\begin{aligned}
&u\leq\frac{1}{3}(1-x)&(x\neq 1)\\
&u \text{は任意}&(x= 1)
\end{aligned}
\right .
\end{aligned}

まず、$h_{green}(x)$がまずい、ということがわかります。安全領域の境界$(x=1)$において、$u$に制約がかからなくなっています。これは、

\begin{aligned}
\dot h_{green}(1)&=\left .\frac{dh_{green}(x)}{dx}\right|_{x=1}\times u\\
&=0\times u\\
-\alpha(h_{green}(1))&=-\alpha(0)\\
&=0
\end{aligned}

であり、境界において制約$\dot{h}(1)= -\alpha(h(1))=0$が$u$に関わらず成り立ってしまうことが原因です。したがって、$h(x)$は境界、すなわち$h(x_b)=0$となるすべての$x=x_b$において$\left .\frac{dh(x)}{dx}\right |_{x=x_b}\neq 0$でなければなりません。 また、$h(x)=k\tilde {h}(x)\,\,\,\,(k>0)$というように、元の制御バリア関数を定数$k$倍して得られる新たな制御バリア関数は、制約を求める際結局$k$が打ち消されます。そのためバリア関数を定数倍することには意味がありません。
それぞれの制御バリア関数に対する$u$の制約を図示すると次のようになります。

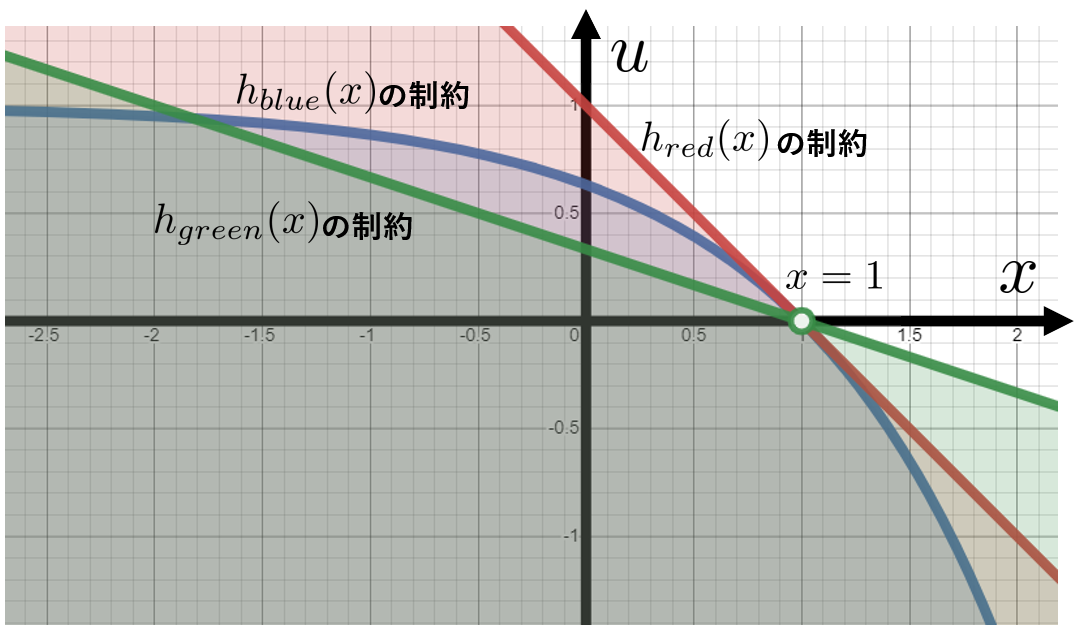
制御バリア関数の設定の仕方次第で、動特性に影響が出ることがわかります。$h_{blue}(x)$では比較的安全性を重視した制御になるようです。

次に、拡張クラスΚ関数$\alpha(h)$の比較を行います。制御バリア関数は$h(x)=1-x$で統一します。今回は2種類の関数を用意します。

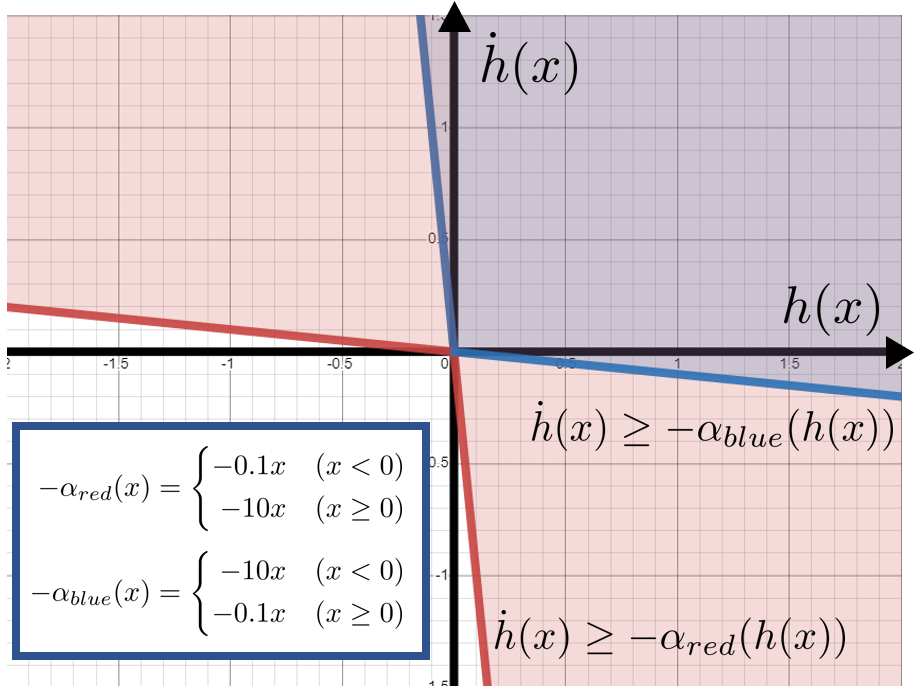
場合分けがあるのが多少面倒ですが、$u$の制約は次のようになります。

$\alpha_{red}(h)$に対する制約:

\begin{aligned}
\dot h(&x)=-u\geq-\alpha_{red}(1-x)\\
&\iff u\leq\alpha_{red}(1-x)\\
&\iff \left\{
\begin{aligned}
&u\leq10(1-x)&(x<1)\\
&u\leq0.1(1-x)&(x\geq 1)
\end{aligned}
\right .
\end{aligned}

$\alpha_{blue}(h)$に対する制約:

\begin{aligned}
\dot h(&x)=-u\geq-\alpha_{blue}(1-x)\\
&\iff u\leq\alpha_{blue}(1-x)\\
&\iff \left\{
\begin{aligned}
&u\leq0.1(1-x)&(x<1)\\
&u\leq10(1-x)&(x\geq 1)
\end{aligned}
\right .
\end{aligned}

よって、それぞれの拡張クラスΚ関数に対する$u$の制約を図示すると次のようになります。

これはまさに本章冒頭の図と同じです。$h(x)$に対する$\dot h(x)$の自由度が、そのまま$u$の自由度に反映されていると考えられるでしょう。$\alpha_{red}(h)$は操作性を、$\alpha_{blue}(h)$は安全性を重視した制御になるようです。
一概に$h(x)$や$α(h)$の良し悪しを決めることは出来ませんが、制御対象の安全性と操作性、どちらを重視したいかによって柔軟に設計することが大切です。

多変数システムの場合

ここまではロボットが1次元上を動くことを前提に話を進めていましたが、2次元平面内を動くロボットにも同じ理論が適用できるでしょうか。ここでは例題として、次のような円状の安全領域内にロボットを留める制御を考えます。

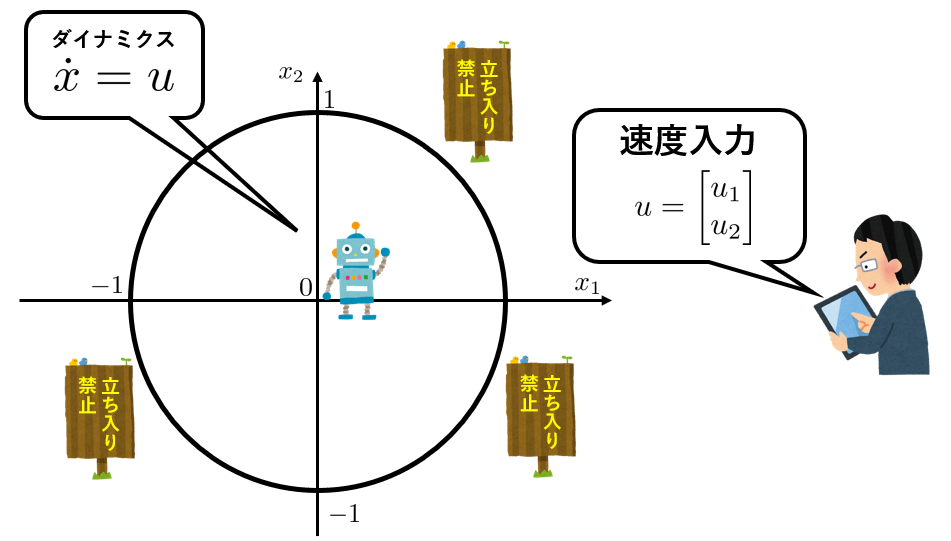
制御バリア関数は

h(x)=1-{x_1}^2-{x_2}^2

でよいでしょう。問題は$\dot h(x)$ですが、これはちょっと難しいです。「$h(x)$を$t$で微分する」とは、時刻が$t\to t+dt$に変化した時、$h(x)$が$h\to h+dh$に変化することを考え、その変化の割合$dh/dt$を求める、ということです。$dh$は次のようなプロセスを踏んで求まります。

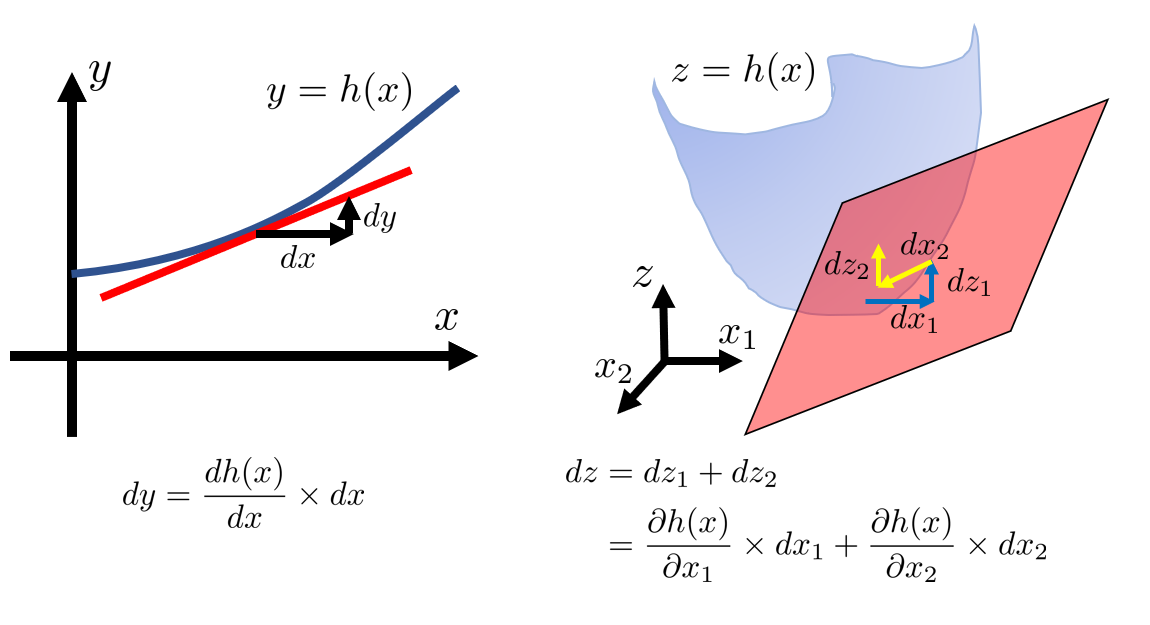
$h(x)$が$x$という1文字の変数からなる関数の時:

1. $dt$は微小なので、$h(x)$も直線に近似して考えてよい。
2. $t\to t+dt$によって、$x$は$dx=\frac{dx}{dt}\times dt$だけ変化する。
3. $x\to x+dx$によって、$h(x)$は$dh=\frac{dh}{dx}\times dx$だけ変化する。
4. 2.を3.に代入すると$dh=\frac{dh}{dx}\times\frac{dx}{dt}\times dt$
5. よって$\frac{dh}{dt}=\frac{dh}{dx}\times\frac{dx}{dt}$となる。

$h(x)$が$x_1, x_2$という2文字の変数からなる関数の時:

1. $dt$は微小なので、$h(x)$も平面に近似して考えてよい。
2. $t\to t+dt$によって、$x_1$は$dx_1=\frac{dx_1}{dt}\times dt$だけ、$x_2$は$dx_2=\frac{dx_2}{dt}\times dt$だけ、変化する。
3. $x_1\to x_1+dx_1$、$x_2\to x_2+dx_2$によって、$h(x)$は$dh=\frac{\partial h}{\partial x_1}\times dx_1+\frac{\partial h}{\partial x_2}\times dx_2$だけ変化する。
4. 2.を3.に代入すると$dh=\frac{\partial h}{\partial x_1}\times \frac{dx_1}{dt}\times dt+\frac{\partial h}{\partial x_2}\times \frac{dx_2}{dt}\times dt$
5. よって$\frac{dh}{dt}=\frac{\partial h}{\partial x_1}\times \frac{dx_1}{dt}+\frac{\partial h}{\partial x_2}\times \frac{dx_2}{dt}$となる。

頭が痛くなりそうな説明ですが、要約すると2変数関数では、曲面を平面に近似することで増加量$dh$を各変数成分による個別の増加量の和で表すことが可能です。 各成分の増加量は、その成分だけに着目した微分、すなわち偏微分で求まるため、比較的簡単に求めることが出来ます。以上を用いると、本例題では$\dot h(x)$は

\begin{aligned}
h(x)&=1-{x_1}^2-{x_2}^2\\
\dot h(x)&=\frac{\partial h}{\partial x_1}\times u_1+\frac{\partial h}{\partial x_2}\times u_2\\
&=-2x_1u_1-2x_2u_2
\end{aligned}

となります。$\alpha(h)=h$とすると、解くべき最適化問題は次のようになります。

minimize\, \,\,\, \|u'-u\|\\
s.t.\,\,\, -2x_1u_1-2x_2u_2\geq-(1-{x_1}^2-{x_2}^2)

一般に、多変数システムの場合は$\dot h(x)$を時間に関する全微分と解釈することで1変数システムと同様に考えられます。

より一般的なダイナミクスに対応する

ここまでは速度入力が出来るロボット、すなわち$\dot x=u$というダイナミクスで動くシステムを前提に考えていました。しかし摩擦や空気抵抗があるシステムでは、必ずしも純粋な速度入力が行えるとは限りません。制御バリア関数は非常に幅広いダイナミクスに対して適用可能ですが、一番効果を発揮できるのは

\dot x=f(x)+g(x)u

という形で書かれるシステム(専門用語で非線形アフィンシステムと言います)までです。実際にこのダイナミクスに基づいて最適化問題を考えることで、この理由を考えていきましょう。

多変数システムを仮定します。制御バリア関数$h(x)$の時間に関する全微分は、

\begin{aligned}
\dot h(x)&=\frac{\partial h}{\partial x_1}\times \dot{x_1}+\frac{\partial h}{\partial x_2}\times \dot{x_2}+\cdots\\
&=\sum_{i=1}^n \frac{\partial h}{\partial x_i}\times \dot{x_i}
\end{aligned}

となります。ここで、$\dot x=f(x)+g(x)u$を次のように書き下します。

\dot x=
\begin{bmatrix}
\dot{x_1}\\\dot{x_2}\\\vdots
\end{bmatrix}=
\begin{bmatrix}
f_1(x)+g_1(x)u_1\\f_2(x)+g_2(x)u_2\\\vdots
\end{bmatrix}

すると$h(x)$の全微分は次のように書けます。

\begin{aligned}
\dot h(x)&=\sum_{i=1}^n \frac{\partial h}{\partial x_i}\times \dot{x_i}\\
&=\sum_{i=1}^n \frac{\partial h}{\partial x_i}\times \left(f_i(x)+g_i(x)u_i\right)
\end{aligned}

つまり、最適化問題として制約$\dot{h}(x)\geq -\alpha(h(x))$を解く時には、コンピューターは$x_1, x_2,\cdots$は全て定数として分かっているわけですから、結果的に

minimize\, \,\,\, \|u'-u\|\\
s.t.\,\,\, 
a_0+a_1u_1+a_2u_2+\cdots+a_nu_n\geq 0

という形式の最適化問題を解くことになるわけです。この$a_0+a_1u_1+a_2u_2+\cdots+a_nu_n\geq 0$という拘束条件は、$n$次元空間を1枚の平面で切り分けた時の、どちらか一方の領域を表します。非常にシンプルな問題なので、(評価関数の複雑さにもよりますが)そこまでの計算量を必要としません。最適化問題は往々にして計算が重くなってしまいがちですが、制御バリア関数による制御は、非線形アフィンシステムというかなり広い定義のシステムに対して、そこそこ軽い最適化問題で解を得ることができるという強みを持っています。

制御バリア関数(実践編)

本章ではここまでで構築した制御バリア関数の知識を用いて、更に発展的な課題に対する実践的な制御設計を行います。

高階微分までしないと制約条件が得られないシステム

次の問題を考えてみましょう。

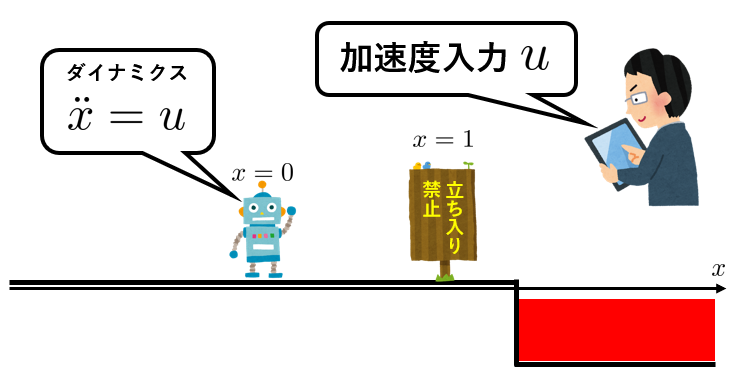
一番最初の問題設定に似ていますが、人間が速度ではなく加速度入力を行うというシチュエーションです。二階微分のダイナミクスは、一階微分連立方程式に書き直すのがセオリーです。

\dot x=
\begin{bmatrix}
\dot{x_1}\\\dot{x_2}\\
\end{bmatrix}=
\begin{bmatrix}
x_2\\u
\end{bmatrix}

$x_1$が位置、$x_2$が速度ですので、$x_2$のー階微分が$u$になります。
さて、今まで通り位置についての制約$h(x)=1-x_1$を制御バリア関数としましょう。$\alpha(h)=h$とすると、

\begin{aligned}
\dot{h}(x)&=\frac{\partial h}{dx_1}\times x_2+\frac{\partial h}{dx_2}\times u\\
&=-x_2\\
\dot{h}(x)&\geq -h(x)\\
\iff -x_2&\geq -(1-x_1)\\
\iff 1-x_1-x_2&\geq 0\\
\end{aligned}

となり、制約条件に$u$が出てきません。そこで、得られた制約条件を新たな安全集合だと思ってもう一度微分してみましょう。
安全集合$C'$を$h_2(x)=1-x_1-x_2$で定義します。同じく$\alpha(h_2)=h_2$として制約を考えます。

\begin{aligned}
\dot{h_2}(x)&=\frac{\partial h_2}{dx_1}\times x_2+\frac{\partial h_2}{dx_2}\times u\\
&=-x_2-u\\
\dot{h_2}(x)&\geq -h_2(x)\\
\iff -x_2-u&\geq -(1-x_1-x_2)\\
\iff u&\leq 1-x_1-2x_2\\
\end{aligned}

これで$u$に関する制約を得られました。$u$の存在範囲は位置$x_1$だけでなく、速度$x_2$に依存して変化することになります。

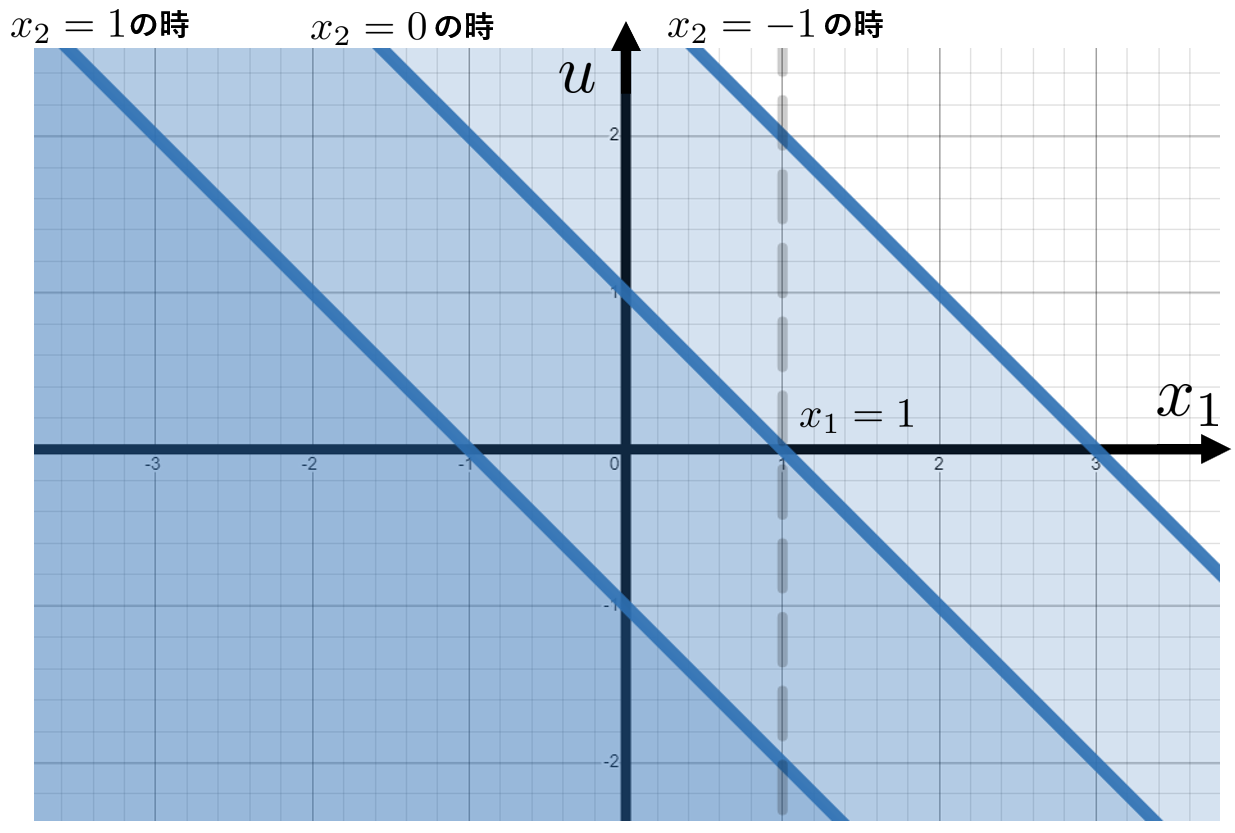
境界付近でロボットが正の速度を持っている場合、かなり大きめに負の加速度入力をして、ブレーキをかけなければなりません。一方境界付近であっても既にロボットが負の速度を持っているなら、正の加速度入力をしても良いはずです。この制約条件は直感的に正しいと言えるでしょう。

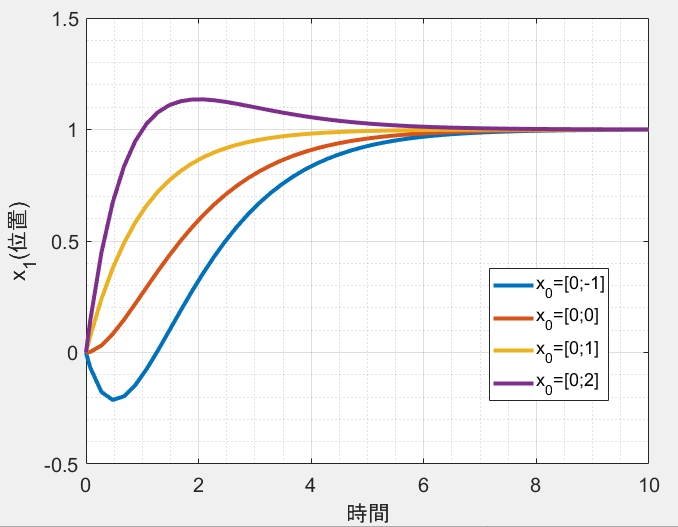
しかしこれで十分でしょうか。例えば時刻$t=0$でロボットが$x_1(0)=0$、$x_2(0)=2$の状態から制御をスタートしたとしましょう。初期条件$x_1(0)=0$、$x_2(0)=2$は、$h(x)=1-x_1>0$を満たしているので、所望の安全集合内から開始しています。先ほどの考察から$u$は$u\leq 1-x_1-2x_2$を満たしていれば良いですから、ロボットに最大入力$u(t)=1-x_1(t)-2x_2(t)$を与え続けましょう。この時のダイナミクスは次のように書けます。可能な限り前に進むような入力ですから、きっと$x_1=1$に収束するはずです。

\dot x=
\begin{bmatrix}
\dot{x_1}\\\dot{x_2}\\
\end{bmatrix}=
\begin{bmatrix}
x_2\\1-x_1-2x_2
\end{bmatrix}

シミュレーションしてみると、応答が$x_1=1$を超えてしまいました(紫の軌道)。初速が異なるその他の3本の軌道は、どれも安全集合を飛び出すことなく$x_1=1$に収束しています。

なぜこんなことが起きてしまったのでしょうか。先ほど私たちは安全領域$C$、すなわち$h(x)\geq 0$を満たすべく、その制約$h_2(x)=\dot{h}(x)+\alpha(h(x))\geq 0$で表される新たな安全領域$C'$を定義しました。この時実は、$C'$は$C$と下図のような関係になっています。

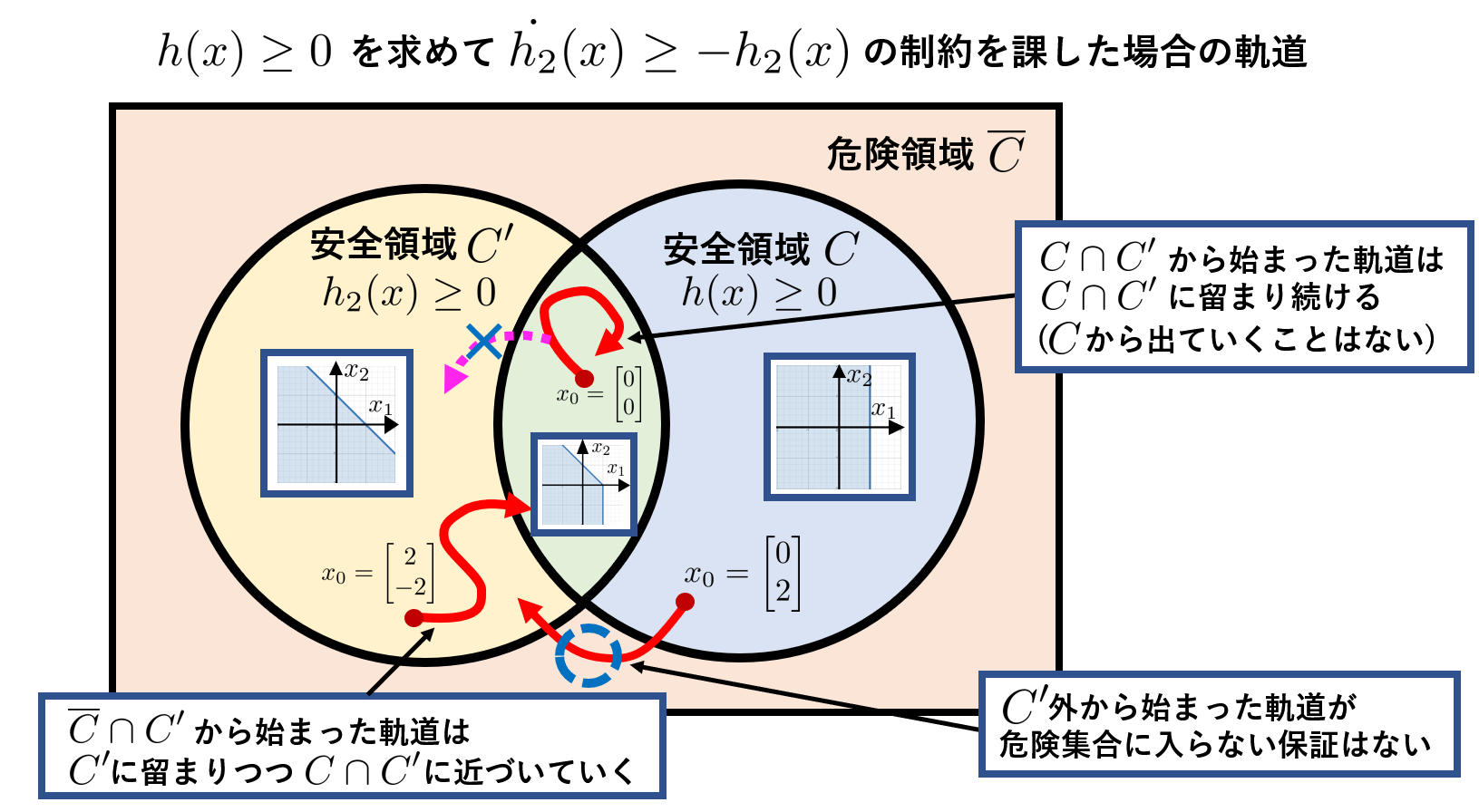
一般に、制御バリア関数やクラスK関数の設計に関わらず、制御バリア関数$h(x)$による制御は、$h(x)$が示す安全領域内からスタートしたものについては領域内に留めることが出来ます。しかし安全領域外からスタートしたものについては、その軌道がどのような範囲に収まるかわかりません。$C'$の安全を満たすべく$\dot{h_2}(x)\geq -\alpha(h_2(x))$を制約に$u$を設計することは、$C\cap \overline{C'}$内、すなわち本来の安全領域$C$内ではあるが$C'$内ではない初期状態に対して安全性を保障できていないのです。初期条件$x(0)=[0, 2]^T$は$C$内の状態ですが、$h_2(x_0)=-1<0$より安全領域$C'$を逸脱しているのでその後オーバーシュートが起きてもおかしくなかった、ということです。

参考
なお、$C\cap C'$内からスタートしたシステムは、必ず$C\cap C'$に留まり続けます。「$C'$に対して制御バリア関数で制御しているのだから、$C'$内でさえあれば入力次第で$C$の境界くらい自由に行き来できるのではないか」と思うかもしれません。ですがそれは$u$に制約がある本条件下では不可能です。これは次のように示せます。

1.初期条件を$x_0\in C\cap C'$とする
2.$\dot{h_2}(x)\geq -\alpha(h_2(x))$かつ$x_0\in C'$より、任意の時刻で$x\in C'$、すなわち$h_2(x)\geq 0$
3.$h_2(x)=\dot{h}(x)+\alpha(h(x))$の定義より、$h_2(x)\geq 0\iff \dot{h}(x)\geq-\alpha(h(x))$
4.$\dot{h}(x)\geq-\alpha(h(x))$かつ$x_0\in C$より、任意の時刻で$x\in C$
5.よって任意の時刻で$x\in C\cap C'$が成り立つ

同様に、それ以外の場所、すなわち$\overline{C\cap C'}$からスタートしたシステムも、集合$C\cap C'$に近づくことが示せます。

1.今、$x\in\overline{C\cap C'}$であるとする。この時、$h(x)<0$または$h_2(x)<0$である
2.$\dot{h_2}(x)\geq -\alpha(h_2(x))$の制御により、$h_2(x)<0\implies \dot{h_2}(x)>0$。したがっていずれは$h_2(x)\geq0$が成立する。
3.$h_2(x)=\dot{h}(x)+\alpha(h(x))$の定義より、$h_2(x)\geq 0\iff \dot{h}(x)\geq-\alpha(h(x))$
4.$\dot{h}(x)\geq -\alpha(h(x))$の成立により、$h(x)<0\implies \dot{h}(x)>0$。したがっていずれは$h(x)\geq0$が成立する。
5.よって時間経過とともにシステムは領域$C\cap C'$に近づく

したがって安全な制御をするためには、初期条件が$x_0\in C\cap C'$であることが肝要となります。

話が難しくなってきましたが、ここで問題点をおさらいしましょう。

加速度入力システムにおいて、$h(x)=1-x_1$を満たす入力$u$を得たい。しかし$\dot{h}(x)\geq -h(x)$という制約式には$u$が現れなかったため、$h_2(x)=\dot{h}(x)+h(x)\geq 0$を改めて目標安全領域として設定し、$\dot{h_2}(x)\geq -h_2(x)$を$u$への制約とすることで一旦の解を得た。だが初期状態がもとの安全領域内であっても、一部の初期状態$\left(x_0\in C\cap\overline{C'}\right)$では$h(x)\geq 0$の安全性が担保できなくなる問題が生じた。

なぜ$x_0\in C\cap \overline{C'}$という初期条件が存在してしまうのでしょうか。それは制約$\dot{h}(x)\geq -\alpha(h(x))$が、$\alpha(h)=h$としたために余裕を持ちすぎているからです。グラフで考えましょう。

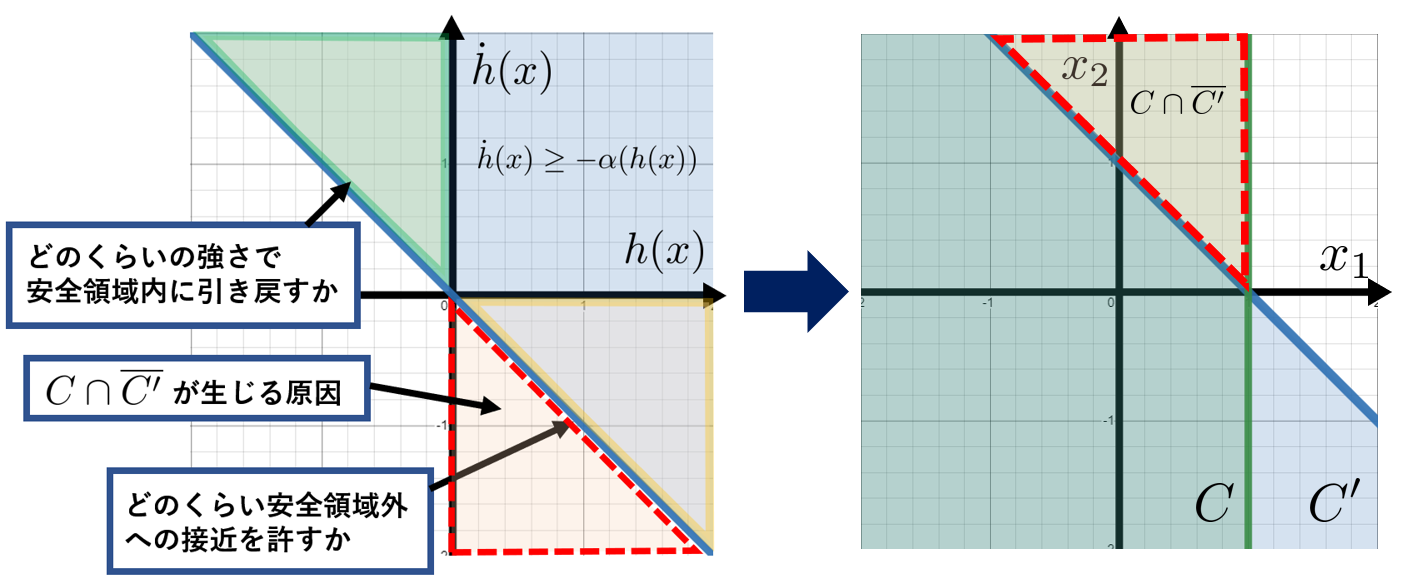
左図の緑の領域は$h(x)<0$、すなわちロボットが危険領域に侵入している状態です。ここでは安全領域に引き戻すような動作が必要になります。$\alpha(h)$の傾きが急なほど、「少しでも安全領域外に出たら大きな$\dot{h}(x)$を要求する」ということになり、結果として安全領域外で大きな入力(状態)制限が生じることが予想できます。一方黄色の領域は$h(x)>0$かつ$\dot{h}(x)<0$、すなわちロボットが安全領域から危険領域に向かって動いている状態です。この部分における$\alpha(h)$の傾きが急なほど、「安全領域の境界すれすれであっても$\dot{h}(x)$が大きく負であることを許容する」ということになり、結果として安全領域内の入力(状態)制限を緩和する方向に働きます(その結果、現実のシステムでは外に飛び出してしまうこともあるかもしれませんが...)。
したがって、左図の赤い領域の状態を許容しない⇒$h_2(x)\geq0$で定義される安全領域$C'$が狭まる⇒右図の赤い領域$C\cap\overline{C'}$が大きくなる、という因果関係があるわけです。赤い領域を減らすためには、最もシンプルな方法として$-\alpha(h)$の傾きを急にするということが考えられます。$k=2$として、先ほどと同じ初期条件でシミュレーションしてみましょう。

\begin{aligned}
\dot{h}(x)&\geq -2h(x)\\
\iff -x_2&\geq -2(1-x_1)\\
\iff 2-2x_1-x_2&\geq 0\\
\end{aligned}

$h_2(x)=2-2x_1-x_2$と定義して、後は同じように$\dot{h_2}(x)\geq -h_2(x)$から制約を得ます。

\begin{aligned}
\dot{h_2}(x)&\geq -h_2(x)\\
\iff -2x_2-u&\geq -(2-2x_1-x_2)\\
\iff u&\leq 2-2x_1-3x_2\\
\end{aligned}

従って最大入力を入れ続けた場合のダイナミクスは次のようになります。

\dot x=
\begin{bmatrix}
\dot{x_1}\\\dot{x_2}\\
\end{bmatrix}=
\begin{bmatrix}
x_2\\2-2x_1-3x_2
\end{bmatrix}

シミュレーションしてみると、$-\alpha(h)=-2h$とした右側の制御では、初期条件$x_0=[0, 2]^T$が$x_0\in C\cap C'$を満たしているためオーバーシュートが無くなっています。

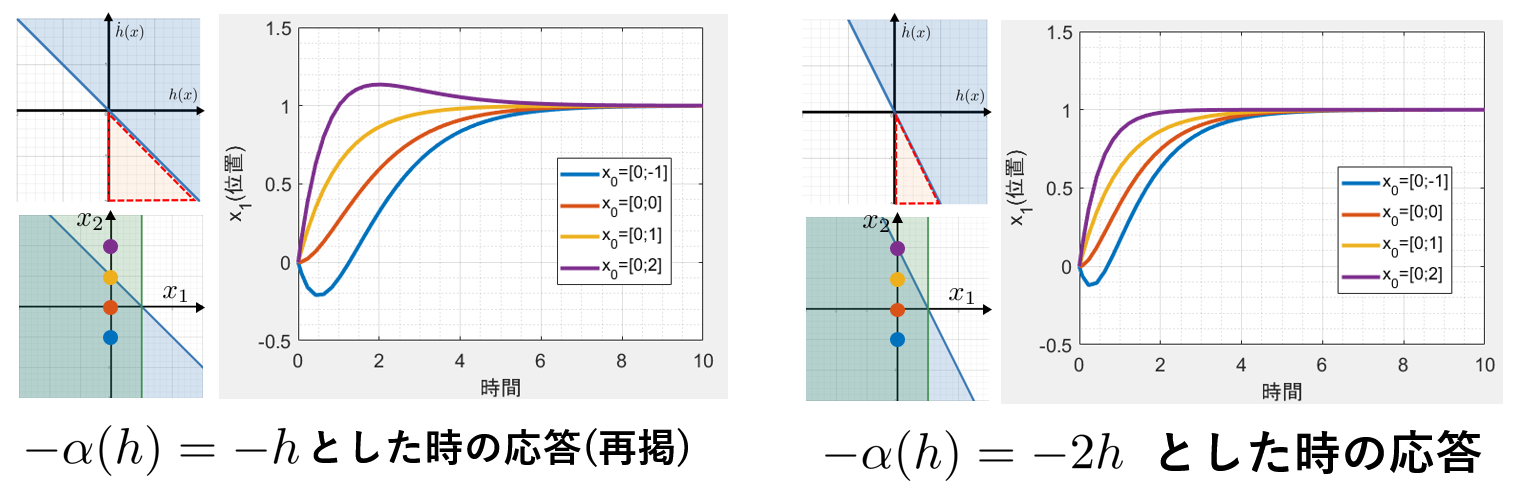
考えたいシステムに応じて適切な$-\alpha(h)$を設計する必要がある良い例となりました。

マルチロボットシステムにおける衝突回避

もう一つ、次のような問題を考えてみます。

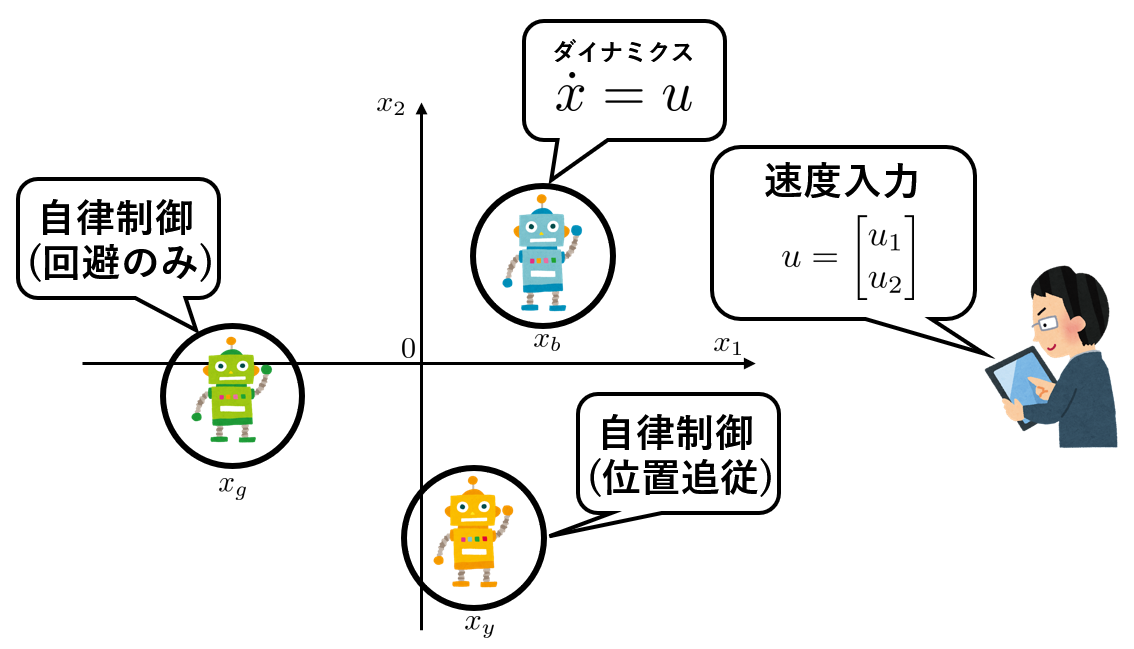
緑と黄色のロボットは自律制御(人間の入力を必要とせず、勝手に動き回る)とし、人間は青いロボットのみに速度を入力します。ロボットは互いに接触すると壊れてしまいますので、それぞれが持つ半径$0.1$の円内には侵入してはいけないものとします。
まずは簡単のため、自分から能動的には動かないが、他者との衝突は回避する緑ロボットを設計します。もう少し具体的に、次のように問題を設定しましょう。

緑ロボットは自機位置$x_g$、及び他2ロボットの位置$x_b$、$x_y$を認識できる。これらを用いてお互いのテリトリーを侵害しないよう、$x_g$に適切な回避入力を与えよ。

さて、今回は制御バリア関数が2本成立します。数学的に2点間$A,B$の距離は$\|A-B\|$で表されます。ここでは計算を楽にするために距離の二乗を評価します。

\begin{aligned}
h_{g1}(x)&=\|x_b-x_g\|^2-0.04\\
&=(x_{b1}-x_{g1})^2+(x_{b2}-x_{g2})^2-0.04\\
h_{g2}(x)&=\|x_y-x_g\|^2-0.04\\
&=(x_{y1}-x_{g1})^2+(x_{y2}-x_{g2})^2-0.04\\
\end{aligned}

緑ロボットは自機以外がどのような速度入力で動いているかは知りませんので、$x_b$や$x_y$は定数として扱います。$\alpha(h)=-h$として$u_g$の制約を考えましょう。

\begin{aligned}
\dot h_{g1}(x)&\geq -h_{g1}(x)\\
-2(x_{b1}-x_{g1})\dot x_{g1}-2(x_{b2}-x_{g2})\dot x_{g2}&\geq -\left ((x_{b1}-x_{g1})^2+(x_{b2}-x_{g2})^2-0.04\right )\\
-2d_{bg1}u_{g1}-2d_{bg2}u_{g2}+\left (\|d_{bg}\|^2-0.04\right )&\geq 0\\\\
\dot h_{g2}(x)&\geq -h_{g2}(x)\\
-2(x_{y1}-x_{g1})\dot x_{g1}-2(x_{y2}-x_{g2})\dot x_{g2}&\geq -\left ((x_{y1}-x_{g1})^2+(x_{y2}-x_{g2})^2-0.04\right )\\
-2d_{yg1}u_{g1}-2d_{yg2}u_{g2}+\left (\|d_{yg}\|^2-0.04\right )&\geq 0\\
\end{aligned}

見やすくするため差分ベクトル$d_{bg}$、$d_{yg}$を用いています。添え字が仰々しいですが、$u_{g1}$、$u_{g2}$に対してこれらはただの直線的な制約です。満たすべき領域が複数の制御バリア関数で定義されるときも、制約の共通部分を満たす入力を求めれば両方の安全性が保障できます。 緑ロボットは能動的には動かず、すなわち目標速度は$[0,0]^T$ですので、入力は次の最適化問題によって与えられます。

minimize\, \,\,\, \|u_g\|\\
s.t.\,\,\, \left\{
\begin{aligned}
-2d_{bg1}u_{g1}-2d_{bg2}u_{g2}+\left (\|d_{bg}\|^2-0.04\right)&\geq 0\\
-2d_{yg1}u_{g1}-2d_{yg2}u_{g2}+\left (\|d_{yg}\|^2-0.04\right)&\geq 0\\
\end{aligned}
\right.

それでは次に、衝突回避をしつつ、人間の速度入力$u_h$を受信する青ロボットを設計します。これも考え方は緑ロボットと全く同じです。目標速度を人間の入力に置き換えるだけですので、少し添え字を弄って入力は次の最適化問題によって与えられます。

minimize\, \,\,\, \|u_b-u_h\|\\
s.t.\,\,\, \left\{
\begin{aligned}
-2d_{yb1}u_{b1}-2d_{yb2}u_{b2}+\left (\|d_{yb}\|^2-0.04\right)&\geq 0\\
-2d_{gb1}u_{b1}-2d_{gb2}u_{b2}+\left (\|d_{gb}\|^2-0.04\right)&\geq 0\\
\end{aligned}
\right.

最後に衝突回避をしつつ、なるべく座標原点$[0,0]^T$に留まるよう、能動的に動く黄色ロボットを考えましょう。自律入力$u_{auto}$は、次のような非常にシンプルな式で表すことが出来ます。

u_{auto}=-x_y

一応証明をしておきましょう。

簡単のため1次元で考える。$\dot x=u, u=-x$のダイナミクスで動くシステムが、$x=0$に収束することを示す。
$x$は時間の関数であり、$\dot x(t)=-x(t)$の解は$x(t)=Ce^{-t}$である。ここで、$C$は任意の定数であり、初期条件$x(0)$が分かっている場合は$C=x(0)$と定まる。
この関数は初期条件に関わらず$t$の増加と共に$0$に収束していくので、$u=-x$を入力としたシステムは$x=0$に収束する。
この事実は$x$をベクトルに拡張しても、成分ごとに同様の証明ができ、成り立つ。

黄色ロボットの制御は、自律入力$u_{auto}$を計算した後、その$u_{auto}$に制御バリア関数による保障をかけてあげることで達成されます。評価関数は$\|u_y-u_{auto}\|$ですが、今回$u_{auto}=-x_y$ですので、解くべき最適化問題は次のようになります。

minimize\, \,\,\, \|u_y+x_y\|\\
s.t.\,\,\, \left\{
\begin{aligned}
-2d_{gy1}u_{y1}-2d_{gy2}u_{y2}+\left (\|d_{gy}\|^2-0.04\right)&\geq 0\\
-2d_{by1}u_{y1}-2d_{by2}u_{y2}+\left (\|d_{by}\|^2-0.04\right)&\geq 0\\
\end{aligned}
\right.

では、これをUnity上で実装してみましょう。Unityで最適化問題を解くには普通それなりの準備が必要ですが、今回くらいの問題設定であれば高校2年生レベルの数学で解けます。

問
$xy$平面上に点$P(a,b)$がある。二つの不等式

s_1x+t_1y+u_1\geq 0 \,\,\,\cdots(1)\\
s_2x+t_2y+u_2\geq 0\,\,\,\cdots(2)\\

によって定義される領域$D$に属す点のうち、点$P$と最も近い距離にあるものを答えよ。
解
解になる可能性があるのは、

• 点$P(a,b)$自身
• 点$P(a,b)$から(1)の境界へ降ろした垂線の足$H_1$、あるいは(2)の境界へ降ろした垂線の足$H_2$
• (1)の境界と(2)の境界の交点$I$

のいずれかである。
$H_1$は、

\left(\frac{at_1^2-bs_1t_1-s_1u_1}{s_1^2+t_1^2},\frac{bs_1^2-as_1t_1-t_1u_1}{s_1^2+t_1^2} \right)

である。同様に$H_2$も計算できる。また$I$は、

\left(\frac{u_1t_2-t_1u_2}{t_1s_2-s_1t_2},\frac{s_1u_2-u_1s_2}{t_1s_2-s_1t_2} \right)

である。下に行くにつれ点$P$から離れていくので、順に計算し、各点が$D$に含まれるか確認すればよい。

この問題のソルバーをC#で書くとこんな感じになります。

クリックでプログラムを確認

    Vector2 rangeoptimizer(Vector2 P,float[] C1, float[] C2)
    {
        //Pが領域内部ならPを返す
        if (isInside(P, C1) && isInside(P, C2)) return P;

        //そうでない場合まず、H1、H2の距離を比較する。
        float[] d = { 10000, 10000, 10000 };
        Vector2 H1 = new Vector2(0, 0);
        if (C1[0]!=0||C1[1] != 0)
        {
            H1.x = P.x * C1[1] * C1[1] - P.y * C1[0] * C1[1] - C1[0] * C1[2];
            H1.y = P.y * C1[0] * C1[0] - P.x * C1[0] * C1[1] - C1[1] * C1[2];
            H1 = H1 / (C1[0] * C1[0] + C1[1] * C1[1]);
        }
        Vector2 H2 = new Vector2(0, 0);
        if (C2[0] != 0 || C2[1] != 0)
        {
            H2.x = P.x * C2[1] * C2[1] - P.y * C2[0] * C2[1] - C2[0] * C2[2];
            H2.y = P.y * C2[0] * C2[0] - P.x * C2[0] * C2[1] - C2[1] * C2[2];
            H2 = H2 / (C2[0] * C2[0] + C2[1] * C2[1]);
        }
        //H1,H2がDに属しているかを確認する。
        if (isInside(H1, C2)) d[0] = Vector2.Distance(P, H1);
        if (isInside(H2, C1)) d[1] = Vector2.Distance(P, H2);
        if (d[0] <= d[1] && d[0] != 10000) return H1;
        if (d[1] <= d[0] && d[1] != 10000) return H2;

        //このどれにも該当しない場合はIが答えになる。
        Vector2 I= new Vector2(0, 0);
        if (C1[1] * C2[0] - C1[0] * C2[1] == 0) return I;
        else
        {
            I.x = C1[2] * C2[1] - C1[1] * C2[2];
            I.y = C1[0] * C2[2] - C1[2] * C2[0];
            I = I / (C1[1] * C2[0] - C1[0] * C2[1]);
            return I;
        }
    }
    bool isInside(Vector2 P, float[] C)
    {
        if (C[0]*P.x+ C[1] * P.y + C[2]>=0)return true;else return false;
    }

3台のロボットの動きを動画で確認してみましょう。

入力に制限がかかり、衝突の回避が出来ています。しかしよく見ると止まっているロボットがびくとも動きません。このままでは状況によってはロボットがスタックしてしまいそうです。

制約の片方の安全距離を$r=0.15$に広げてみましょう。$0.15^2=0.09$ですから、例えば緑ロボットは次のような制約式になります。

minimize\, \,\,\, \|u_g\|\\
s.t.\,\,\, \left\{
\begin{aligned}
-2d_{bg1}u_{g1}-2d_{bg2}u_{g2}+\left (\|d_{bg}\|^2-0.09\right)&\geq 0\\
-2d_{yg1}u_{g1}-2d_{yg2}u_{g2}+\left (\|d_{yg}\|^2-0.04\right)&\geq 0\\
\end{aligned}
\right.

こうすることで、緑色ロボットは、青色ロボットが半径$0.15$の自分のテリトリーに入ってきた時点で回避行動をとるようになります。

これでスタックする心配がなくなりました。

全体のコードはこちら

クリックで全体のプログラムを確認

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class colisionavoldu : MonoBehaviour
{
    public int mode;
    public GameObject friend1;
    public GameObject friend2;
    public Vector2 p;
    // Start is called before the first frame update
    void Start()
    {
    }

    // Update is called once per frame
    void Update()
    {
        p = new Vector2(0, 0);
        if (mode == 1)
        {
        }
        else if (mode == 2)
        {
            if (Input.GetKey(KeyCode.UpArrow)) p.y += 1;
            if (Input.GetKey(KeyCode.RightArrow)) p.x += 1;
            if (Input.GetKey(KeyCode.DownArrow)) p.y -= 1;
            if (Input.GetKey(KeyCode.LeftArrow)) p.x -= 1;
            p.Normalize();
        }
        else if (mode == 3)
        {
            p.x = -0.4f*this.transform.position.x;
            p.y = -0.4f*this.transform.position.z;
        }
        Vector3 delta1 = friend1.transform.position-this.transform.position;
        Vector3 delta2 = friend2.transform.position-this.transform.position;
        float[] cs1 = new float[3];
        float[] cs2 = new float[3];
        cs1[0] = -2 * delta1.x;
        cs1[1] = -2 * delta1.z;
        cs1[2] = 10f*(Vector3.Magnitude(delta1)* Vector3.Magnitude(delta1) - 0.04f);
        cs2[0] = -2 * delta2.x;
        cs2[1] = -2 * delta2.z;
        cs2[2] = 10f*(Vector3.Magnitude(delta2) * Vector3.Magnitude(delta2) - 0.09f);

        Vector2 v2 = rangeoptimizer(p, cs1, cs2);
        Vector3 v3 = new Vector3(v2.x, 0,v2.y);
        this.transform.position +=v3 * Time.deltaTime;
    }


    //点Pの座標、拘束式(s,t,uの順に2本)を引数にする。
    Vector2 rangeoptimizer(Vector2 P,float[] C1, float[] C2)
    {
        //Pが領域内部ならPを返す
        if (isInside(P, C1) && isInside(P, C2)) return P;

        //そうでない場合まず、H1、H2の距離を比較する。
        float[] d = { 10000, 10000, 10000 };
        Vector2 H1 = new Vector2(0, 0);
        if (C1[0] != 0 || C1[1] != 0) 
        {
            H1.x = P.x * C1[1] * C1[1] - P.y * C1[0] * C1[1] - C1[0] * C1[2];
            H1.y = P.y * C1[0] * C1[0] - P.x * C1[0] * C1[1] - C1[1] * C1[2];
            H1 = H1 / (C1[0] * C1[0] + C1[1] * C1[1]);
        }
        Vector2 H2 = new Vector2(0, 0);
        if (C2[0] != 0 || C2[1] != 0)
        {
            H2.x = P.x * C2[1] * C2[1] - P.y * C2[0] * C2[1] - C2[0] * C2[2];
            H2.y = P.y * C2[0] * C2[0] - P.x * C2[0] * C2[1] - C2[1] * C2[2];
            H2 = H2 / (C2[0] * C2[0] + C2[1] * C2[1]);
        }
        //H1,H2がDに属しているかを確認する。
        if (isInside(H1, C2)) d[0] = Vector2.Distance(P, H1);
        if (isInside(H2, C1)) d[1] = Vector2.Distance(P, H2);
        if (d[0] <= d[1] && d[0] != 10000) return H1;
        if (d[1] <= d[0] && d[1] != 10000) return H2;

        //このどれにも該当しない場合はIが答えになる。
        Vector2 I= new Vector2(0, 0);
        if (C1[1] * C2[0] - C1[0] * C2[1] == 0) return I;
        else
        {
            I.x = C1[2] * C2[1] - C1[1] * C2[2];
            I.y = C1[0] * C2[2] - C1[2] * C2[0];
            I = I / (C1[1] * C2[0] - C1[0] * C2[1]);
            return I;
        }
    }
    bool isInside(Vector2 P, float[] C)
    {
        if (C[0]*P.x+ C[1] * P.y + C[2]>=0)return true;else return false;
    }
}

おわりに

制御バリア関数の理論は、本来は不変性や安定性など様々な前提理論の上に成り立っています。ですが単純な問題設定を考えればそう取っつきにくいものではありません。幅広いシステムに対して線形制約に対する最適化だけで安全が保障できるというのは非常に魅力的なことです。ぜひ習得しておきたい知識といえます。

なお、万能なように見える制御バリア関数ですが、実は定式化が大変という大きなデメリットもあります。予め$\dot{h(x)}$を手作業で微分しておかないと、$u$に関する制約を得られないからです。また応用編で確認したように、制御バリア関数による制御は$h(x)$や$\alpha(h)$の設計によって操作性が悪くなることもあり得ます。便利なものだからこそ、しっかり理解した上で使いたいものです。