はじめに
kaggleのチュートリアルであるタイタニック号の生存者予測にチャレンジしてみました。
今回は機械学習のモデルを組んで生存確率を予測するのではなく、データ同士の関係を見て、どのような人が生き残ったのかを調べていきます。
そして得られた結果を欠損値の補完や特徴量生成をする際に利用していきたいと思います。
追記 : kaggleのtitanicについては以下の3つの記事を書きました。予測値を出すところまでやっているのでよろしければこちらも御覧ください。
kaggleのtitanic xgboostを使った生存者予測 [80.1%]
kaggleのtitanic ニューラルネットを使った生存者予測 [80.4%]
kaggleのtitanic スタッキングを使った生存者予測[81.3%]
1. データの概要
ライブラリをインポートしてtrainデータを読み込み&確認
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
data=pd.read_csv("/kaggle/input/titanic/train.csv")
data.head()
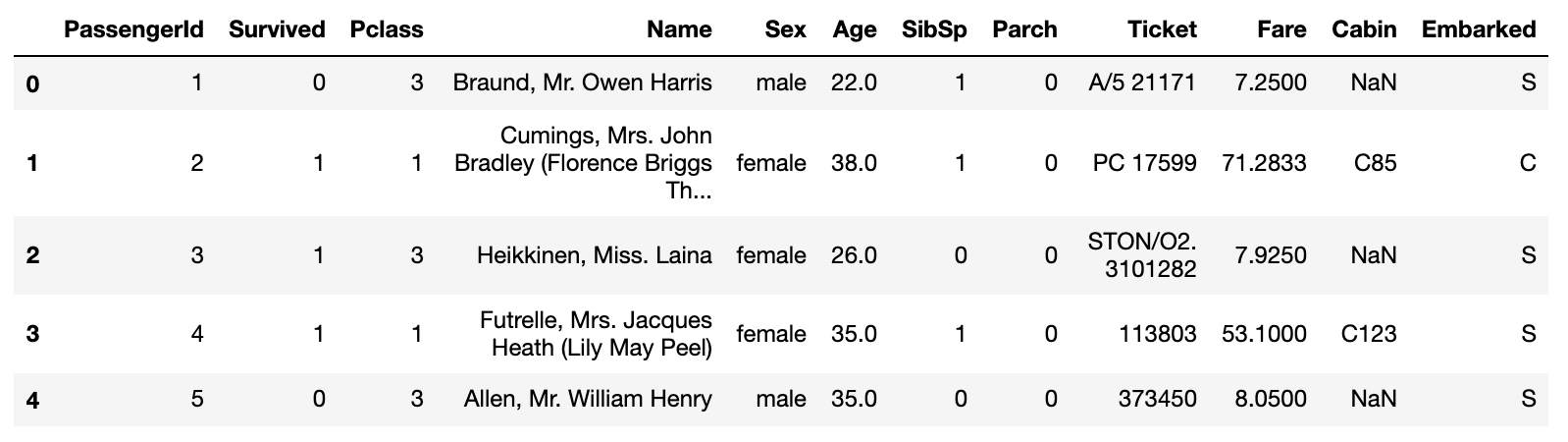
特徴量の種類
・PassengerId : 乗客のID
・Survived : 生死(0:死亡,1:生存)
・Pclass : 乗客の社会階級(1:Upper, 2:Middle, 3:Lower)
・Name : 名前
・Sex : 性別
・Age : 年齢
・SibSp : 一緒に乗っている兄弟、配偶者の数
・Parch : 一緒に乗っている親、子供の数
・Ticket : チケットの番号
・Fare : 乗船料
・Cabin : 客室番号
・Embarked : 乗船した港
はじめにデータの欠損値、要約統計量、各特徴量同士の相関係数を見てみます。
# 欠損値を確認
data.isnull().sum()
| 欠損値の数 | |
|---|---|
| PassengerId | 0 |
| Survived | 0 |
| Pclass | 0 |
| Name | 0 |
| Sex | 0 |
| Age | 177 |
| SibSp | 0 |
| Parch | 0 |
| Ticket | 0 |
| Fare | 0 |
| Cabin | 687 |
| Embarked | 2 |
# 要約統計量を確認
# 最大値や最小値、平均値、分位数が確認できる
# 欠損値がある場合は除外して計算される
data.describe()
| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| count | 891.000000 | 891.000000 | 891.000000 | 714.000000 | 891.000000 | 891.000000 | 891.000000 |
| mean | 446.000000 | 0.383838 | 2.308642 | 29.699118 | 0.523008 | 0.381594 | 32.204208 |
| std | 257.353842 | 0.486592 | 0.836071 | 14.526497 | 1.102743 | 0.806057 | 49.693429 |
| min | 1.000000 | 0.000000 | 1.000000 | 0.420000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 223.500000 | 0.000000 | 2.000000 | 20.125000 | 0.000000 | 0.000000 | 7.910400 |
| 50% | 446.000000 | 0.000000 | 3.000000 | 28.000000 | 0.000000 | 0.000000 | 14.454200 |
| 75% | 668.500000 | 1.000000 | 3.000000 | 38.000000 | 1.000000 | 0.000000 | 31.000000 |
| max | 891.000000 | 1.000000 | 3.000000 | 80.000000 | 8.000000 | 6.000000 | 512.329200 |
# 各特徴量の相関係数を確認
data.corr()
| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| PassengerId | 1.000000 | -0.005007 | -0.035144 | 0.036847 | -0.057527 | -0.001652 | 0.012658 |
| Survived | -0.005007 | 1.000000 | -0.338481 | -0.077221 | -0.035322 | 0.081629 | 0.257307 |
| Pclass | -0.035144 | -0.338481 | 1.000000 | -0.369226 | 0.083081 | 0.018443 | -0.549500 |
| Age | 0.036847 | -0.077221 | -0.369226 | 1.000000 | -0.308247 | -0.189119 | 0.096067 |
| SibSp | -0.057527 | -0.035322 | 0.083081 | -0.308247 | 1.000000 | 0.414838 | 0.159651 |
| Parch | -0.001652 | 0.081629 | 0.018443 | -0.189119 | 0.414838 | 1.000000 | 0.216225 |
| Fare | 0.012658 | 0.257307 | -0.549500 | 0.096067 | 0.159651 | 0.216225 | 1.000000 |
相関係数からSurvivedと関係のある特徴量を見たいのですが数字だけの表だとちょっとわかりづらいですね...
ですのでこの表のかぶっている値を取り除き、絶対値表記にしたものをヒートマップで表してみます。
# 値を絶対値にする
corr_matrix = data.corr().abs()
# 下三角行列をつくり、corr_matrixに当てはめる
map_data = corr_matrix.where(np.tril(np.ones(corr_matrix.shape), k=-1).astype(np.bool))
# 画像の大きさを決めてヒートマップに変換
plt.figure(figsize=(10,10))
sns.heatmap(map_data, annot=True, cmap='Greens')
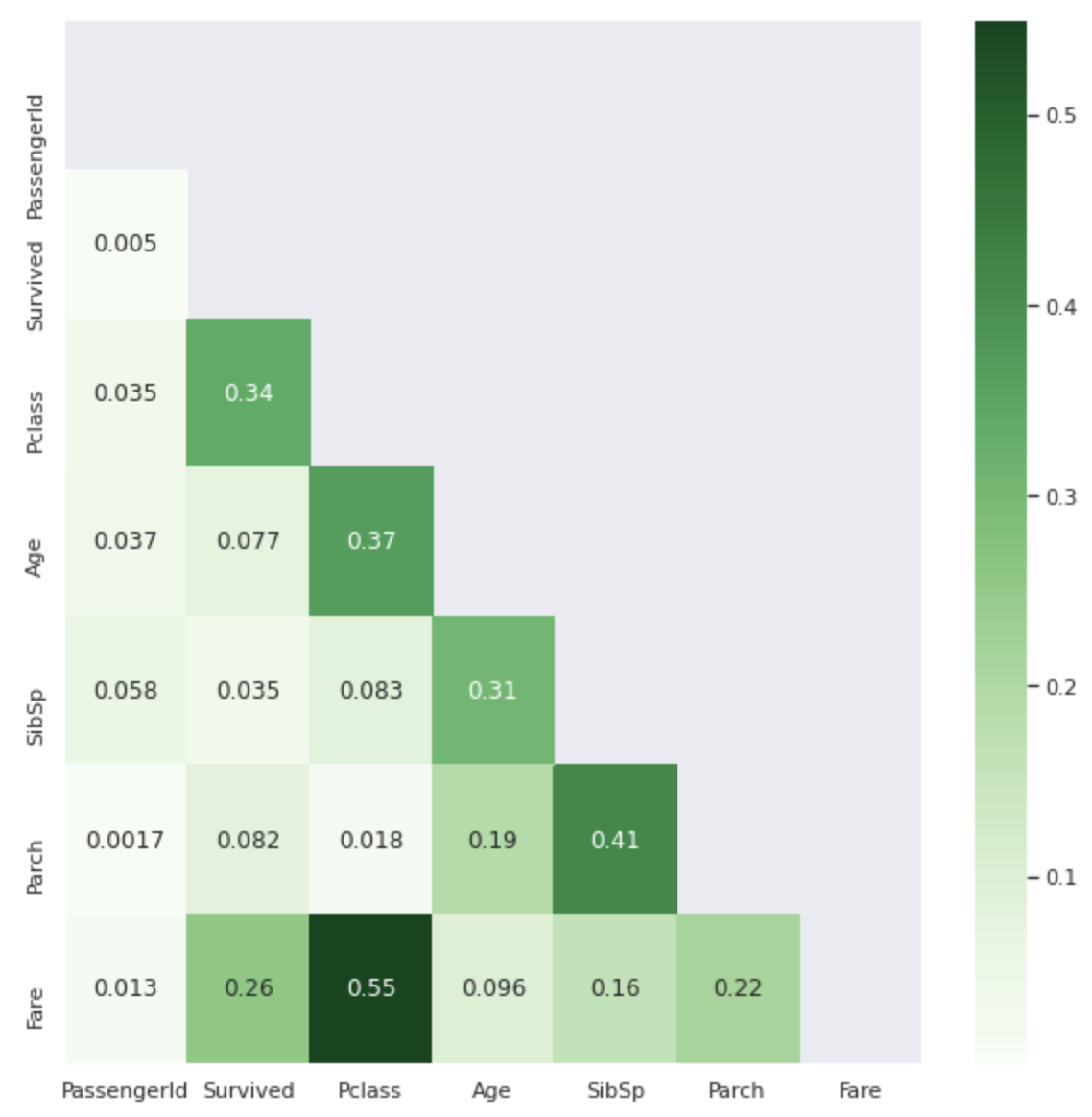
色の濃い部分ほど相関係数の値が1に近くなっています。
.corr( )の表よりも見やすくなったのではないでしょうか。
特徴量が数値でないもの(Name,Sex,Ticket,Cabin,Embarked)に関してはわかりませんが、上の表からSurvivedに大きく関与しているのはPclassとFareだということが読み取れます。
2. Pclass
まずPclassとSurvivedの関係を確認します。
sns.barplot(x='Pclass',y='Survived',hue='Sex', data=data)

Pclassが高い人ほど生存率が高いですね。
階級が上の人ほど優先的に助けられたということでしょうか。
また、どの階級においても女性の生存率が男性の倍以上あることがわかります。
ちなみに全体での男性の生存率は18.9%、女性の生存率は74.2%でした。
3. Fare
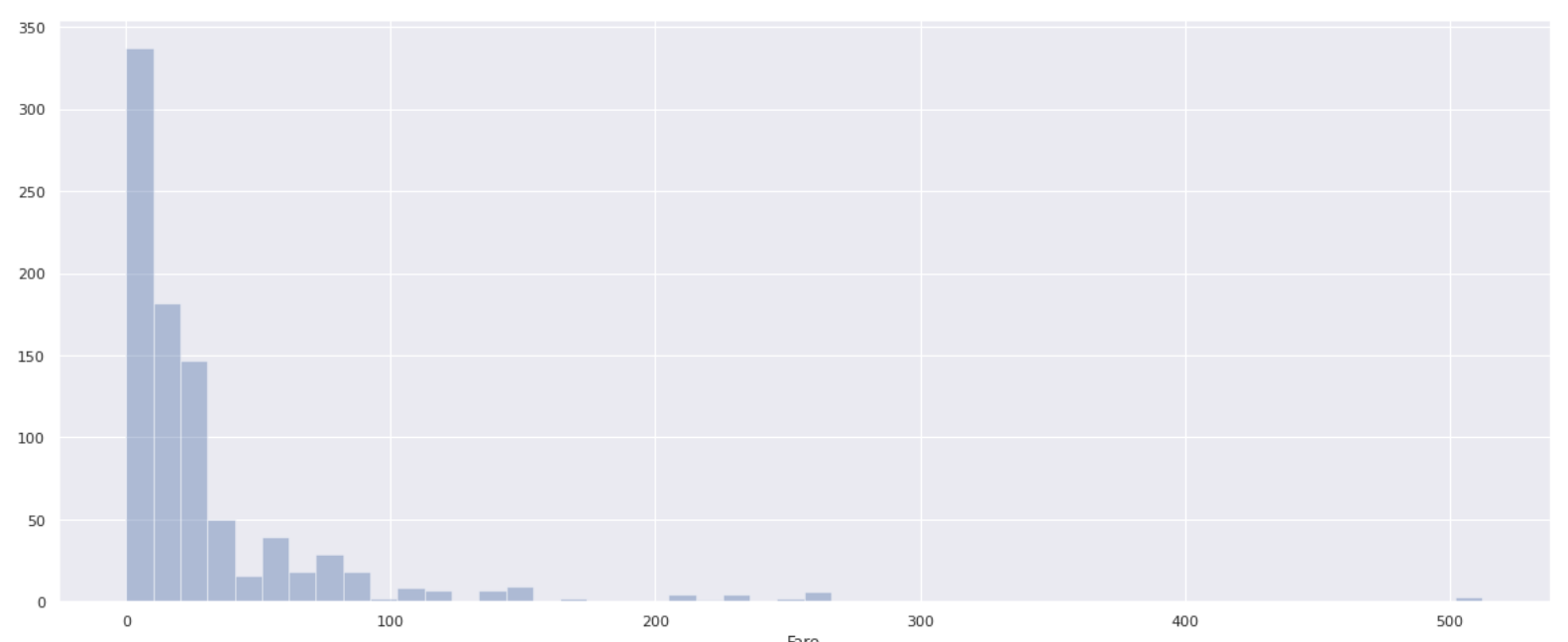
最小値が0、最大値が512と幅広いので全体的な分布を調べてみます。
plt.figure(figsize=(20,8))
sns.distplot(data['Fare'], bins=50, kde=False)
乗船料が100を超えている人たちは少なく、ほとんどの乗客の乗船料は0~100であることがわかります。
乗船料によって生存率がどう変わるかを調べるためにFareの値を10ずつ区分け(0~10, 10~20, 20~30・・・)してそれぞれの生存率を求めます。
# 10ずつに区分けした'Fare_bin'の列をdataに追加
data['Fare_bin'] = pd.cut(data['Fare'],[i for i in range(0,521,10)], right=False)
bin_list = []
survived_list = []
for i in range(0,511,10):
#各区間における生存率を求める
survived=data[data['Fare_bin'].isin([i])]['Survived'].mean()
#NaNになっている区間を除外して生存率を求められる区間だけをリストに追加
if survived >= 0:
bin_list.append(f'{i}~{i+10}')
survived_list.append(survived)
# 2つのリストからデータフレームをつくってグラフへ
plt.figure(figsize=(20,8))
fare_bin_df = pd.DataFrame({'Fare_bin':bin_list, 'Survived':survived_list})
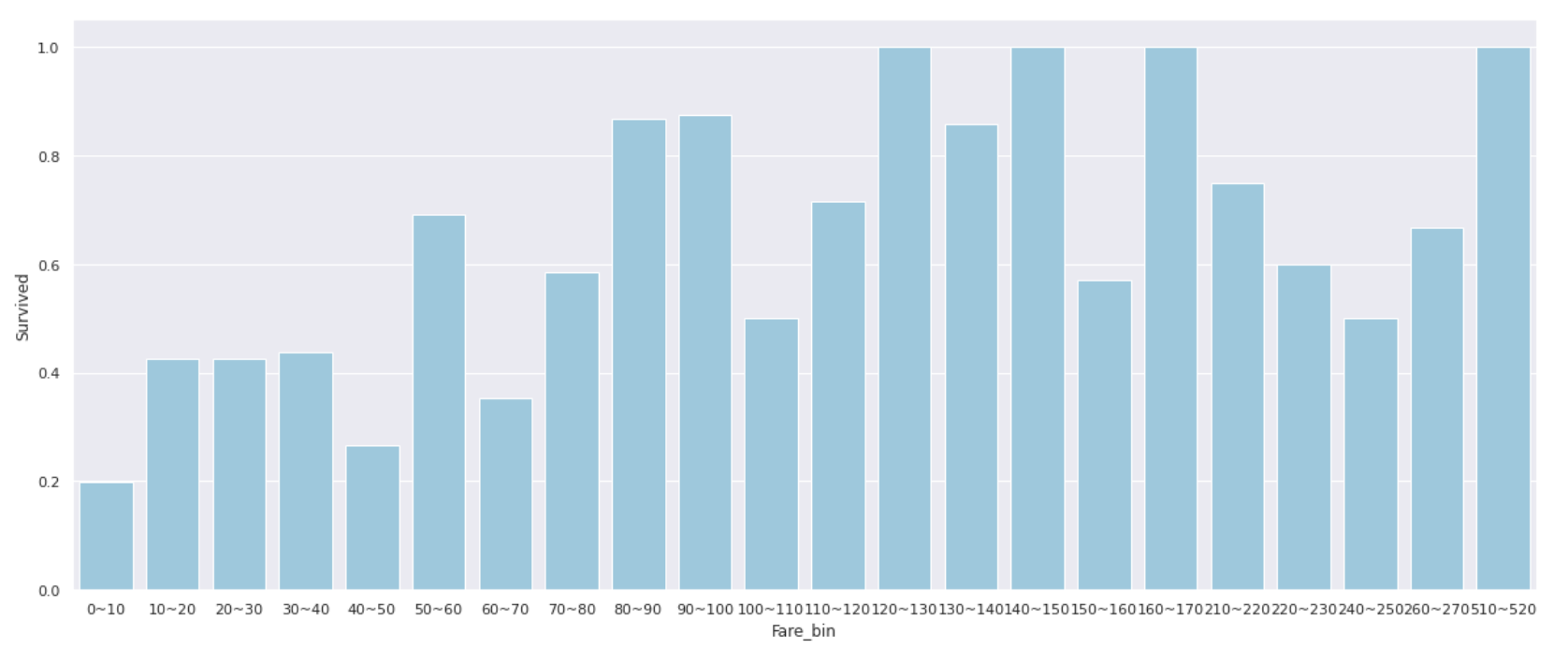
sns.barplot(x='Fare_bin', y='Survived', data=fare_bin_df, color='skyblue')
Fareが0~10の人は生存率が20%以下と極端に低く、Fareが50を超えてくると生存率が50%を上回る場合が多くなるようです。
値をそのまま使うのではなく、0~10の人は'Low',10~50の人は'Middle'というように__クラス分けしたものを特徴量として使う__のもいいかもしれません。
また、PclassとFareの相関係数も0.55となっていたのでついでにその2つの関係を見てみると下のグラフのようになりました。
(※Fareが100以上の人のPclassは全て1だったので割愛)
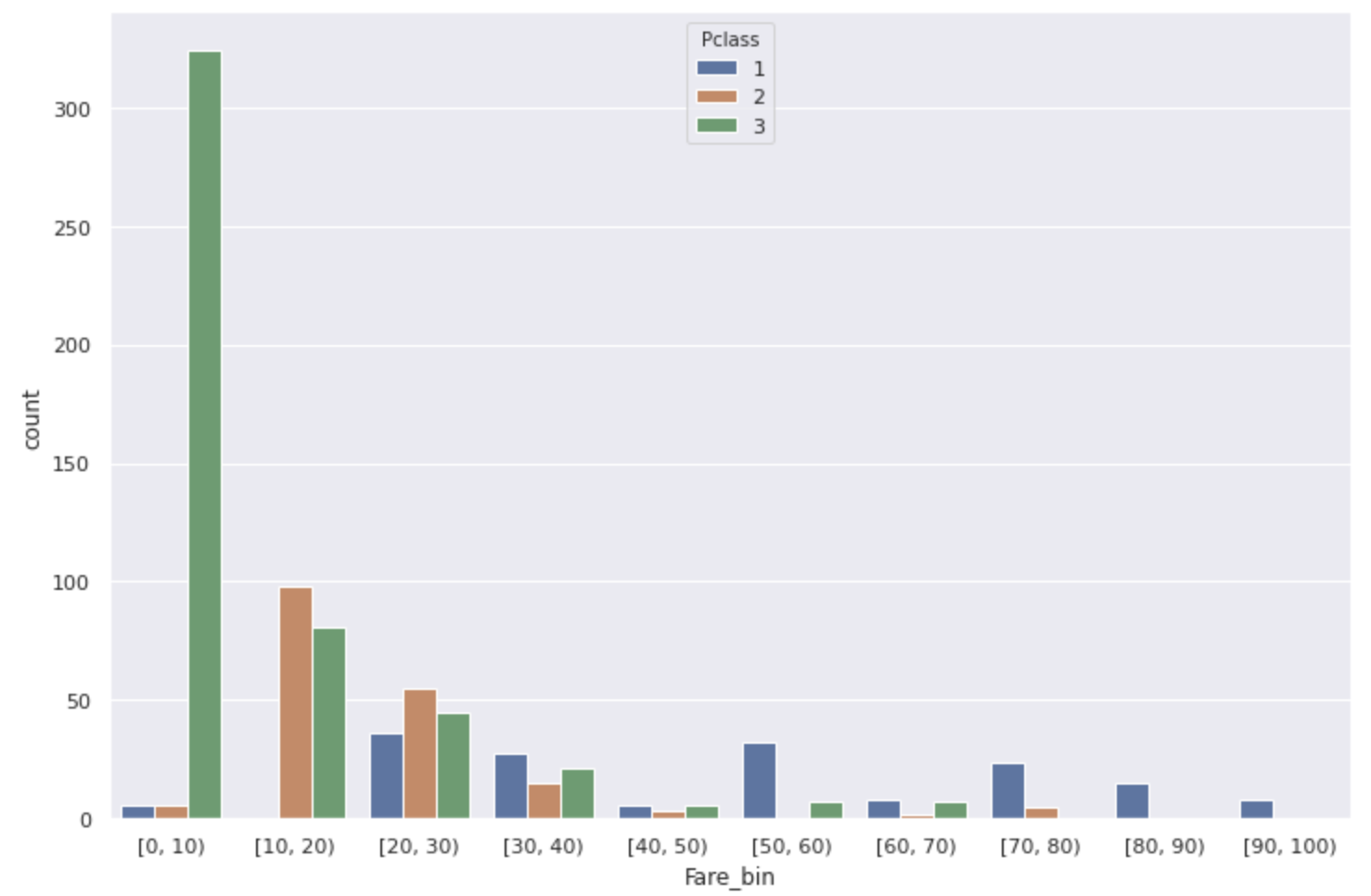
やはり生存率の低いFare[0,10)のほとんどは階級の低い人たちですね。
さらにSurvivedとFare_binのグラフで生存率が1.0になっているところのデータを見てみると名字が共通していたり、チケット番号が同じになっています。
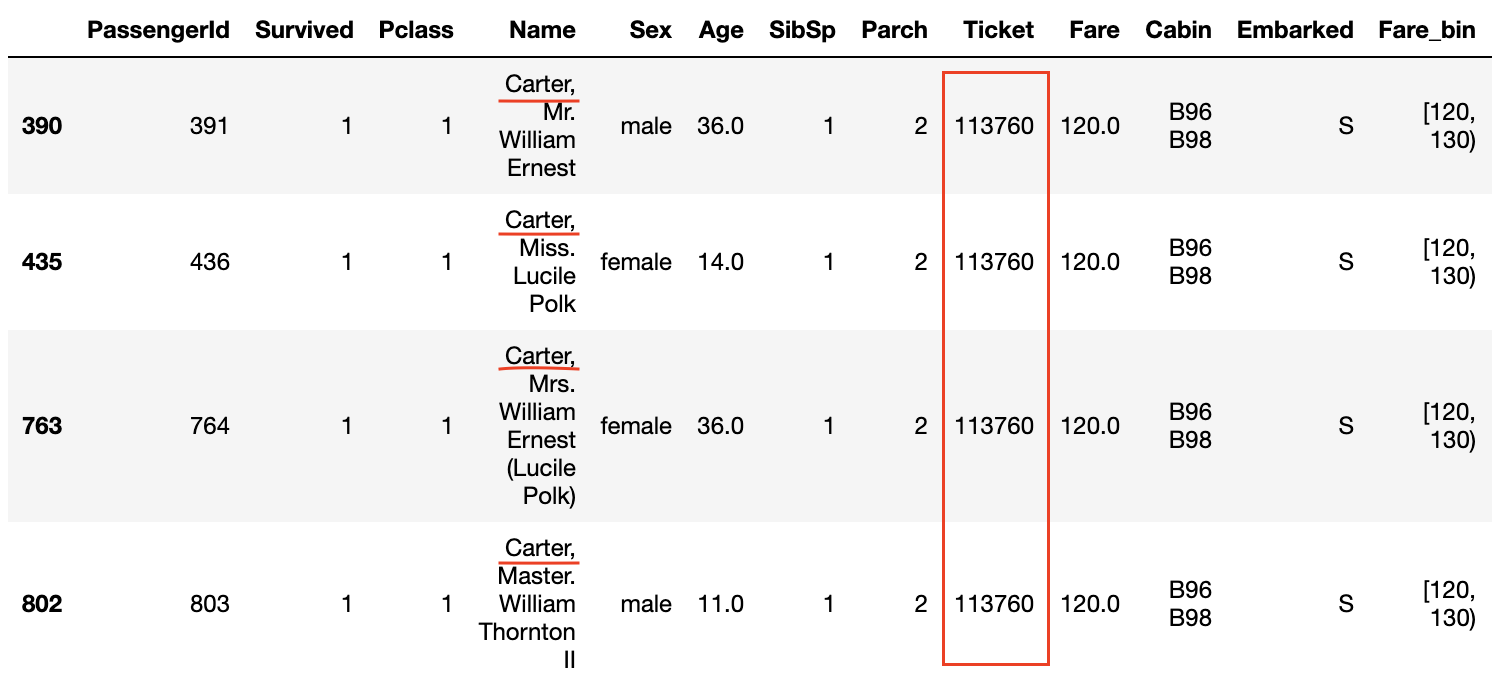
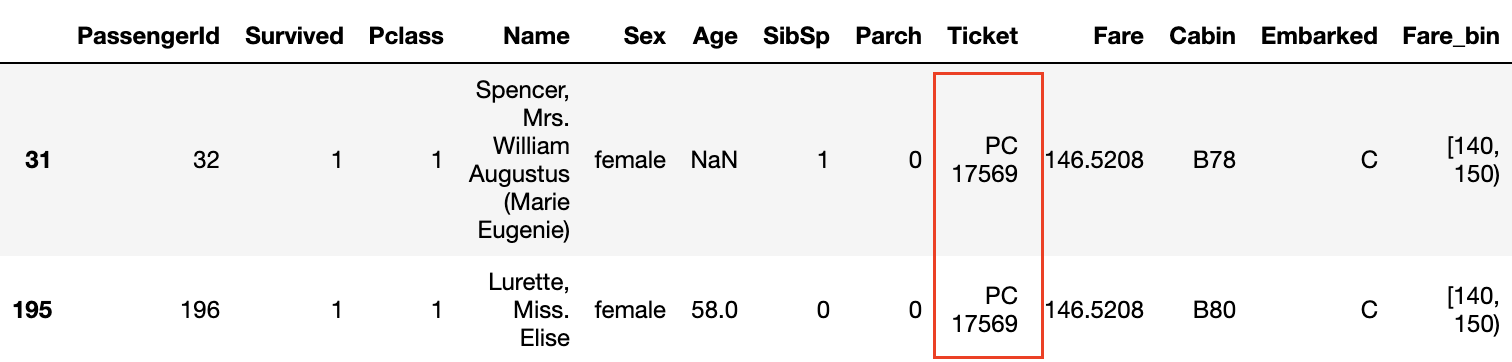

また、Pclassが3でFareが高くない場合でもチケット番号が同じであれば生存率が高いように思われます。
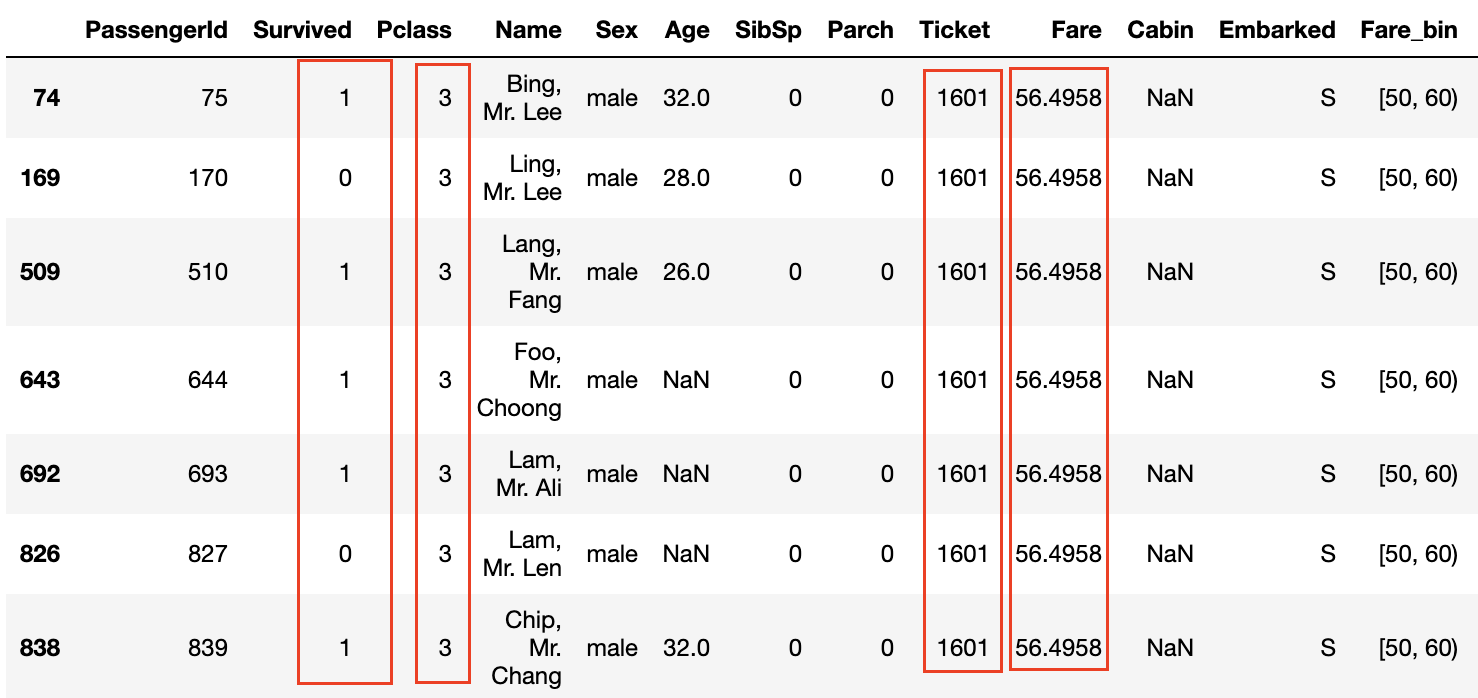
チケット番号が同じということは家族や友人同士で一緒にチケットを購入したということであり、船内でも行動をともにしたり、船から逃げるときも助け合ったりすることができたということになりそうです。
では、家族の人数やチケットの番号によって生存率に違いがあるのか調べてみましょう。
4. SibSPとParch
タイタニックのデータにもとからあるSibSpとParchの値を使って何人家族でタイタニックに乗船したかという特徴量'Family_size'をつくってみます。
# Family_sizeの特徴量を作成
data['Family_size'] = data['SibSp']+data['Parch']+1
fig,ax = plt.subplots(1,2,figsize=(20,8))
# 生存者と死亡者の数をグラフ化
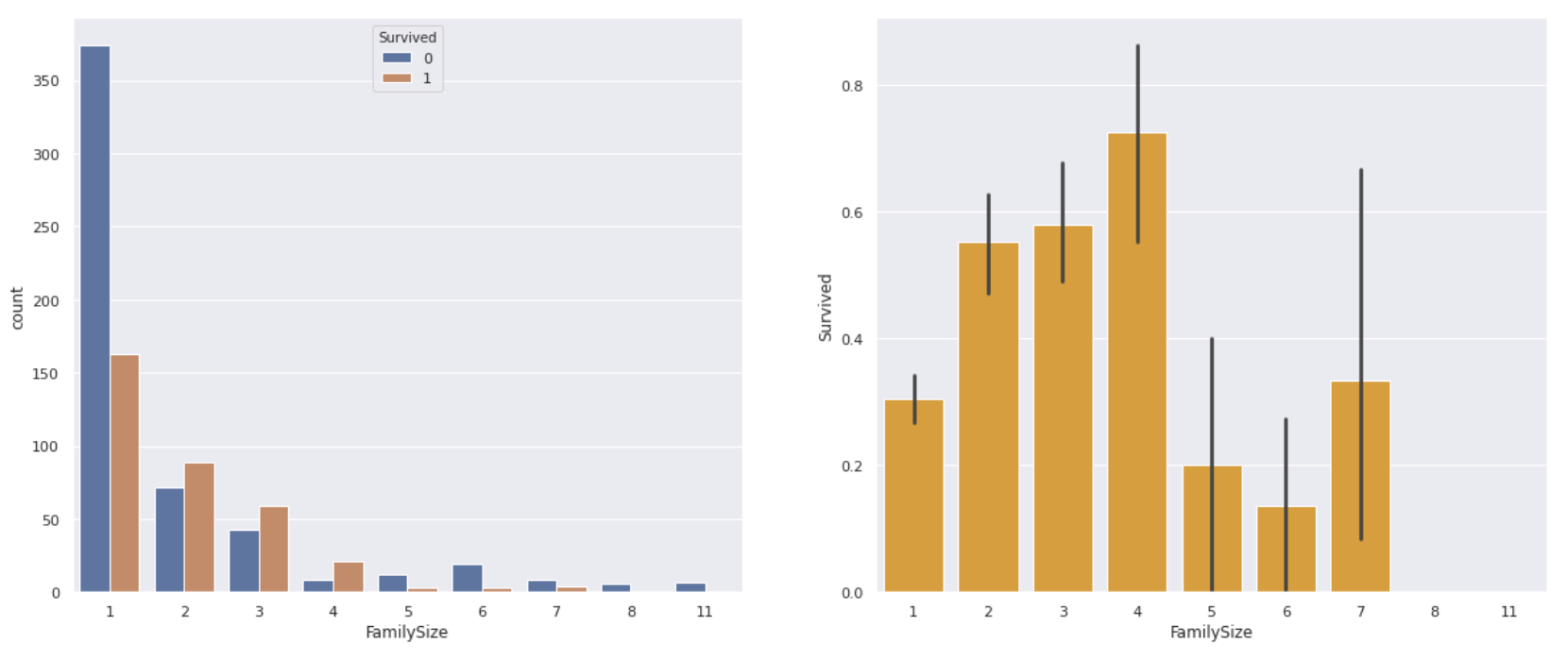
sns.countplot(data['Family_size'],hue=data['Survived'], ax=ax[0])
# Family_sizeごとの生存率を求める
sns.barplot(x='Family_size', y='Survived',data=data, color='orange', ax=ax[1])
**1人で乗っていた人は家族と乗っていた人に比べて生存率が低く、4人家族の場合が最も生存率が高くなりました。**逆に家族の人数が多すぎると、まとまって行動するのが難しかったのか生き残ることはできなかったようです。
これもFareと同じように家族の人数に応じて4つぐらいにクラス分けすると特徴量として利用できそうです。
5. Ticket
チケット番号が重複している数を'Ticket_count'の列に入れていきます
これによって家族だけではなく、(おそらく)友人同士で乗船した人たちの生存率も合わせて見ることができそうです。
# Ticket_countの列を作成
data['Ticket_count'] = data.groupby('Ticket')['PassengerId'].transform('count')
# 生存率を求める
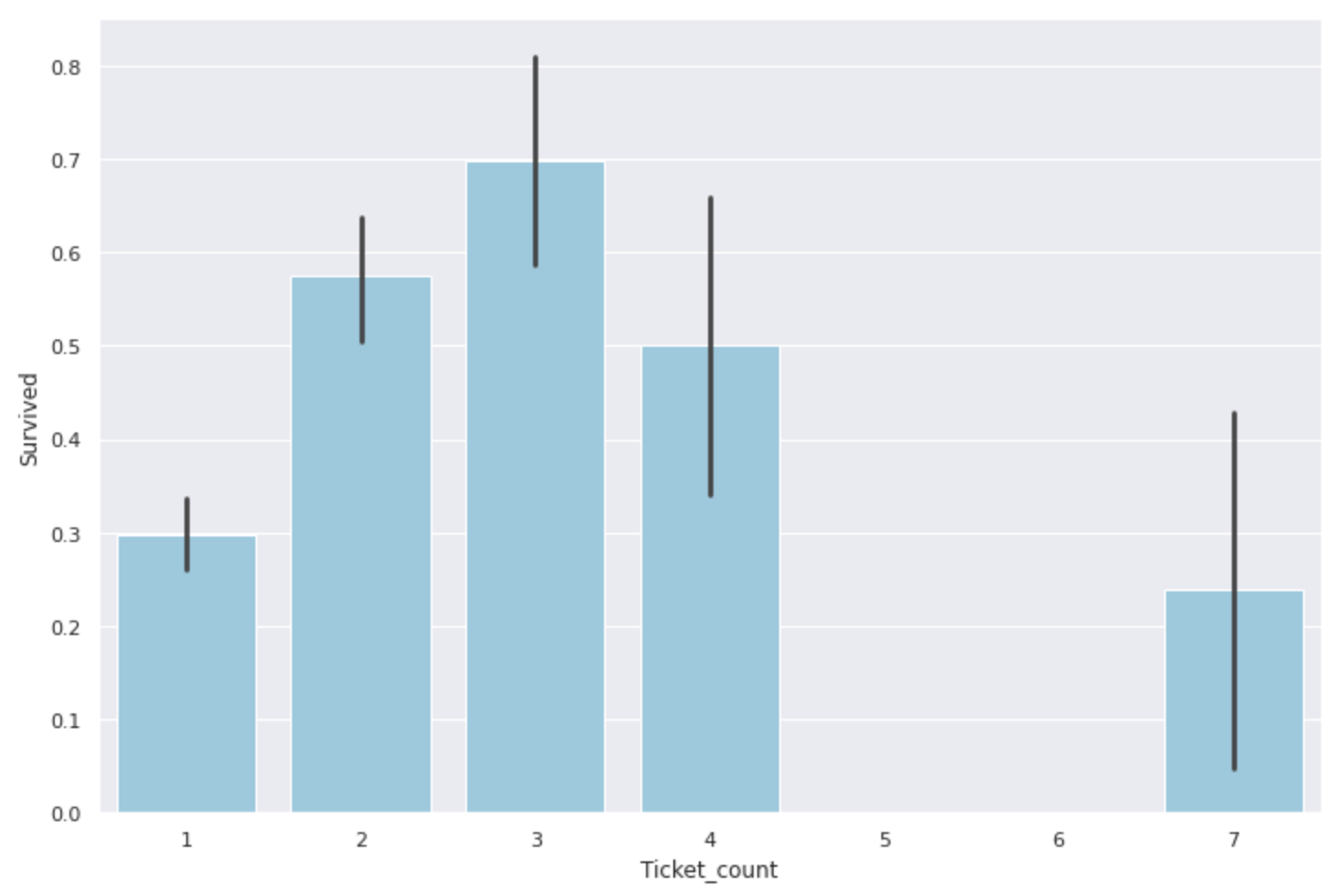
plt.figure(figsize=(12,8))
sns.barplot(x='Ticket_count', y='Survived',data=data, color='skyblue')
家族の人数で比べたときと同じように2~4人の団体が最も助かりやすく、1人で来ている人、または5人以上の団体は生存率が低いようです。
これもFareやFamily_sizeと同様にクラス分けしたものが特徴量として使えます。
ここで、チケットから得られる情報を深堀りしてみましょう。
Ticketの細かい区分にはこちらのサイトを参考にさせていただきました。
pyhaya’s diary : Kaggleのタイタニックデータの解析
チケット番号には数字だけのものと数字&アルファベットのものがあるので、それらを分類します。
# 数字のみのチケットを取得
num_ticket = data[data['Ticket'].str.match('[0-9]+')].copy()
num_ticket_index = num_ticket.index.values.tolist()
# 元のdataから数字のみのチケットの行を落とした残りがアルファベットを含むチケット
num_alpha_ticket = data.drop(num_ticket_index).copy()
まず、数字のみのチケット番号がどのような分布になっているのかを見てみます。
# チケット番号は文字列で入力されているので数値に変換
num_ticket['Ticket'] = num_ticket['Ticket'].apply(lambda x:int(x))
plt.figure(figsize=(12,8))
sns.jointplot(x='PassengerId', y='Ticket', data=num_ticket)
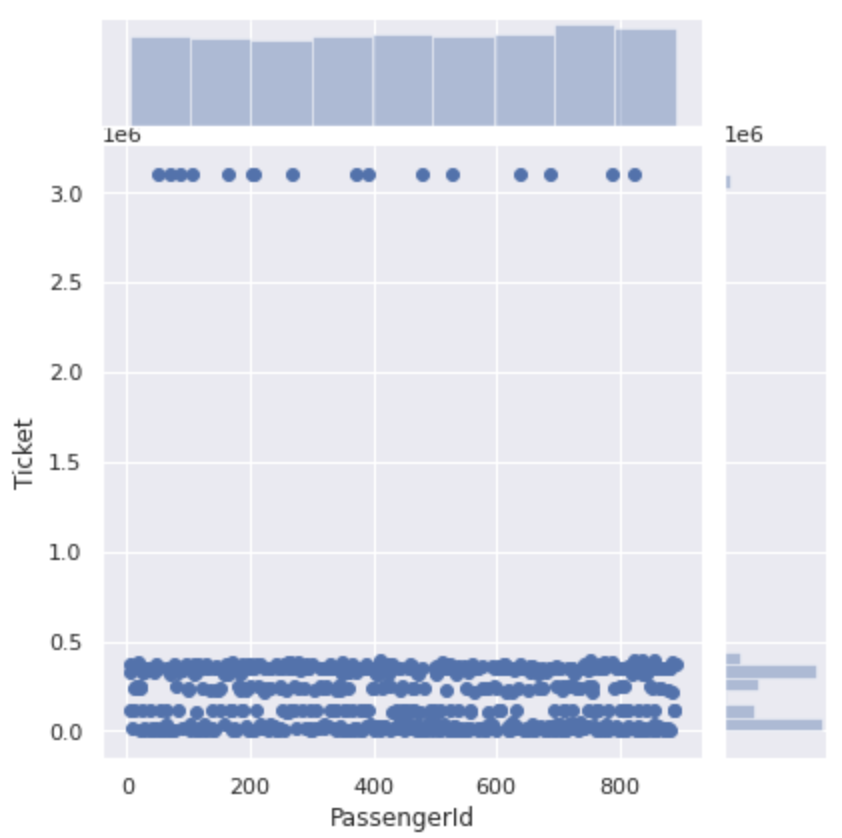
大きく分けて500000以下の番号と3000000以上の番号に分けられています。
さらに0~500000の区間を細かく見ると、この区間のチケット番号は4つに分かれています。
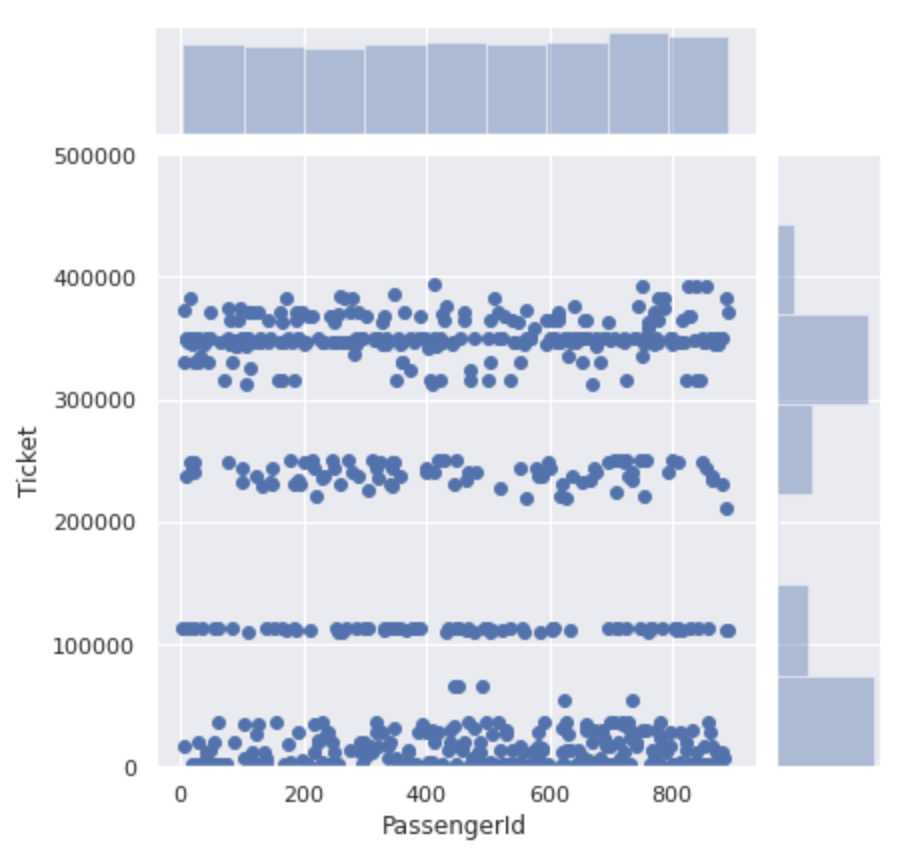
チケット番号は単に連番というわけではなく番号ごとのまとまりがあるようです。
これもまとまりごとにクラス分けをしてそれぞれの生存率の違いを見てみましょう。
# 0~99999の番号のチケットは0のクラス
num_ticket['Ticket_bin'] = 0
num_ticket.loc[(num_ticket['Ticket']>=100000) & (num_ticket['Ticket']<200000),'Ticket_bin'] = 1
num_ticket.loc[(num_ticket['Ticket']>=200000) & (num_ticket['Ticket']<300000),'Ticket_bin'] = 2
num_ticket.loc[(num_ticket['Ticket']>=300000) & (num_ticket['Ticket']<400000),'Ticket_bin'] = 3
num_ticket.loc[(num_ticket['Ticket']>=3000000),'Ticket_bin'] = 4
plt.figure(figsize=(12,8))
sns.barplot(x='Ticket_bin', y='Survived', data=num_ticket)
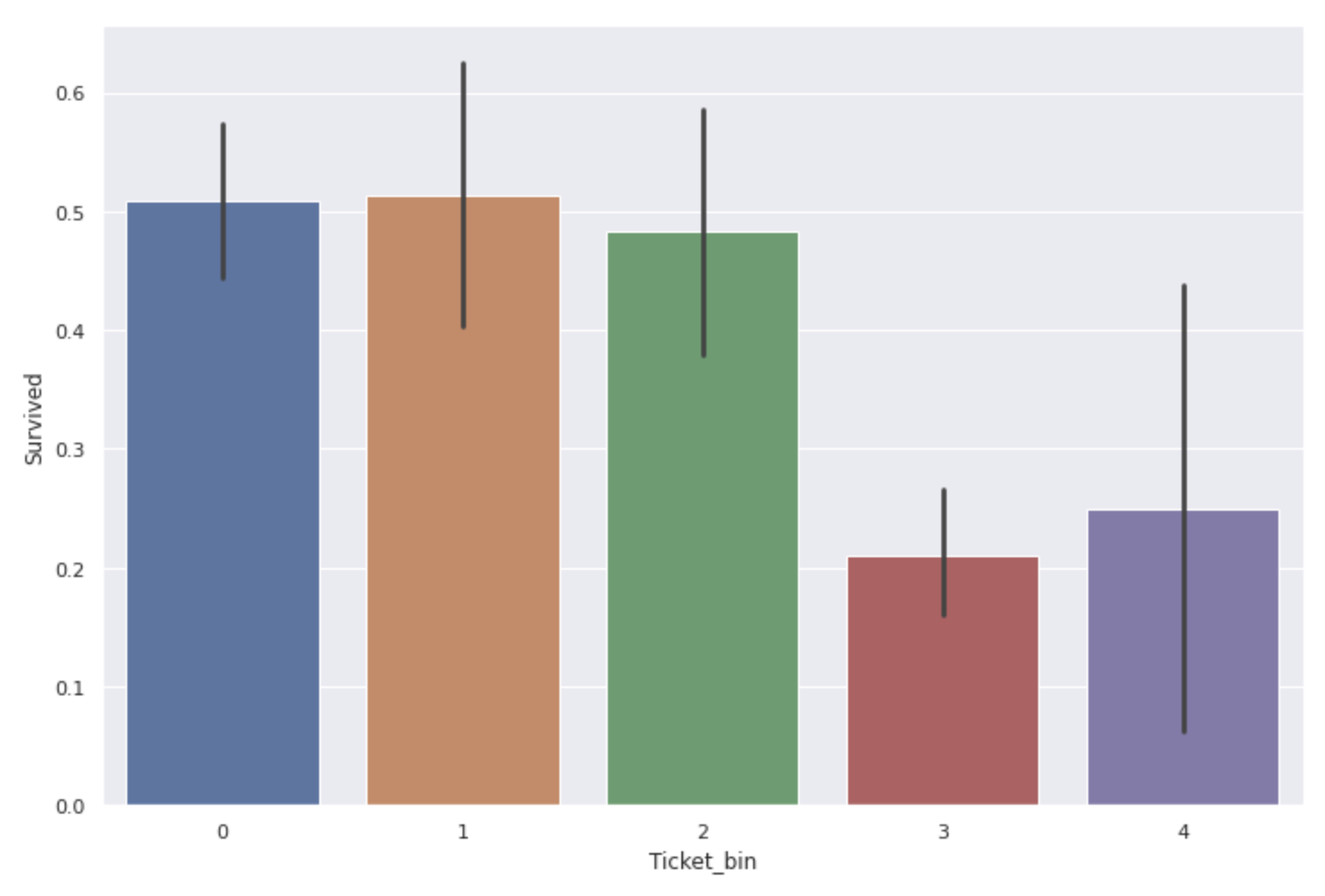
300000~400000と3000000以上のチケット番号の人の生存率がかなり低くなっています。
次に数字&アルファベットのチケットについても同様に調べていきます。
まず、どんな種類があるのかを確認します。
# 種類ごとに見やすくするためにsortする
sorted(num_alpha_ticket['Ticket'].value_counts().items())
種類が多いのである程度数があるものには1~10のクラスをそれぞれに与え、それ以外の数が少ないものはまとめて0のクラスにしました。
num_alpha_ticket['Ticket_bin'] = 0
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('A.+'),'Ticket_bin'] = 1
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('C.+'),'Ticket_bin'] = 2
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('C\.*A\.*.+'),'Ticket_bin'] = 3
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('F\.C.+'),'Ticket_bin'] = 4
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('PC.+'),'Ticket_bin'] = 5
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('S\.+.+'),'Ticket_bin'] = 6
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('SC.+'),'Ticket_bin'] = 7
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('SOTON.+'),'Ticket_bin'] = 8
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('STON.+'),'Ticket_bin'] = 9
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('W\.*/C.+'),'Ticket_bin'] = 10
plt.figure(figsize=(12,8))
sns.barplot(x='Ticket_bin', y='Survived', data=num_alpha_ticket)
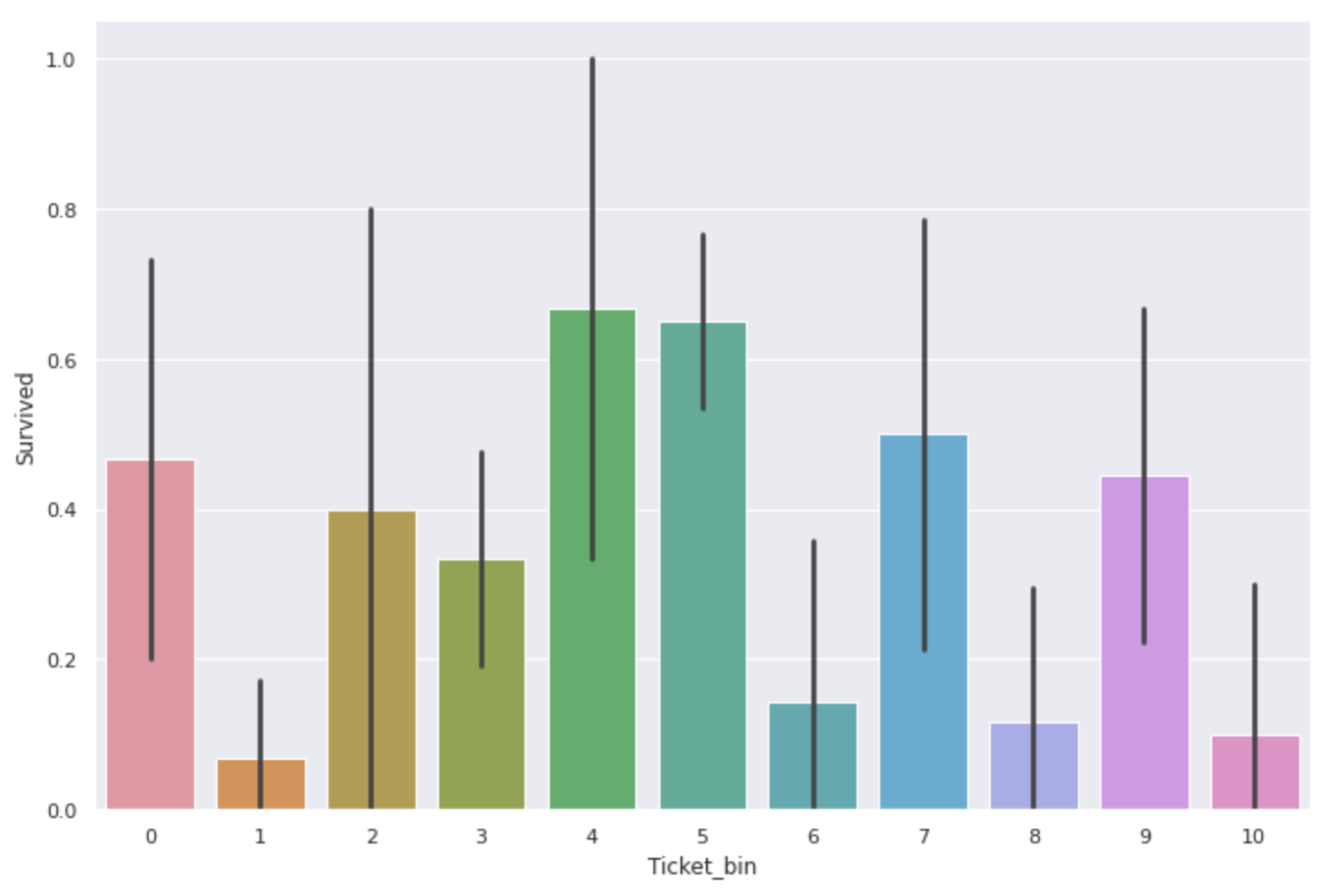
こちらも同様に生存率の違いが出ました。'F.C'と'PC'がついたものは特に高いですね。
ただ、アルファベットを含むチケットのデータは全体でも230個しかなく、数字のみのチケットに比べるとデータ数が3分の1ほどしかないので生存率の値そのものの信憑性はあまりないかもしれません。
チケット番号によって生存率が変わるのは部屋の場所やランクによって番号が分けられているからだと思われます。
ここでチケットと関係がありそうなPclassとFareについてそれぞれ関係を見てみます。
↓数字のみのチケットについて
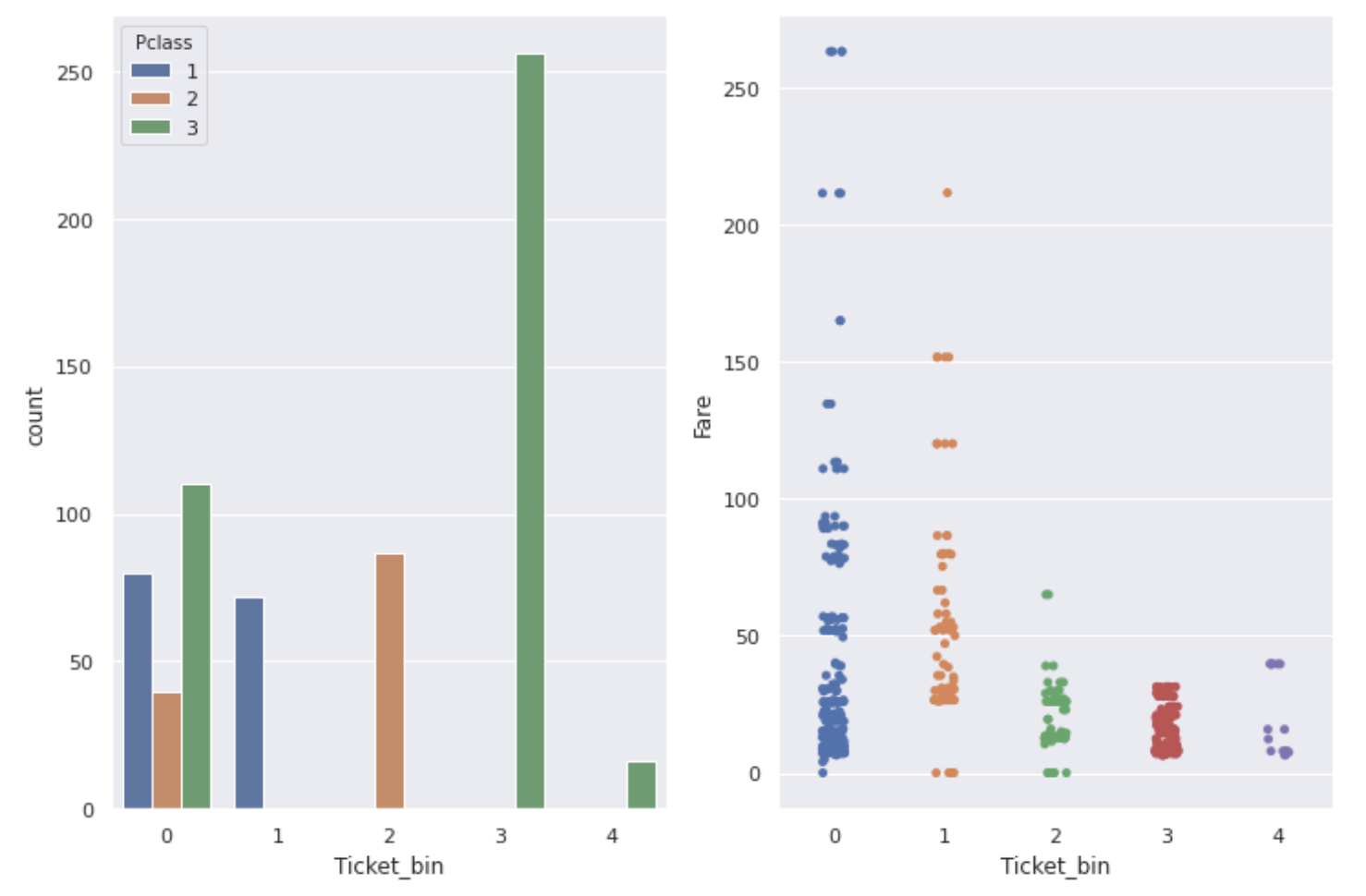
fig,ax = plt.subplots(1,2,figsize=(12,8))
sns.countplot(num_ticket['Ticket_bin'], hue=num_ticket['Pclass'], ax=ax[0])
sns.stripplot(x='Ticket_bin', y='Fare', data=num_ticket, ax=ax[1])
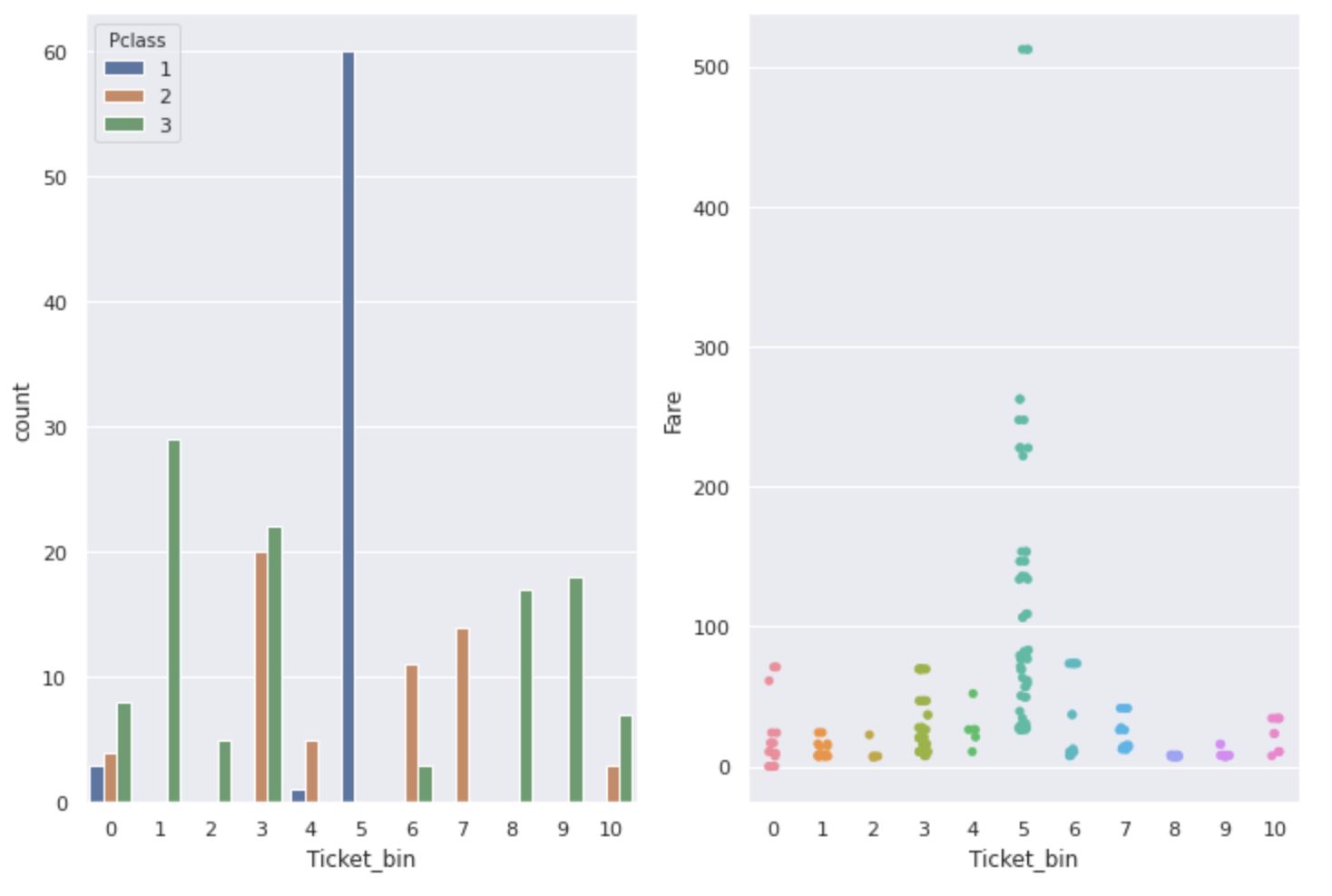
fig,ax = plt.subplots(1,2,figsize=(12,8))
sns.countplot(num_alpha_ticket['Ticket_bin'], hue=num_alpha_ticket['Pclass'], ax=ax[0])
sns.stripplot(x='Ticket_bin', y='Fare', data=num_alpha_ticket, ax=ax[1])
グラフからわかるようにTicket,Pclass,Fareの3つは互い関係があり、特に生存率が高いチケット番号はFareも高く、Pclassが1の人がほとんどです。
一見役立たなそうなチケット番号も、このように探ってみると十分有用な特徴量になるのではないでしょうか。
6. Age
欠損値が含まれているのでひとまず欠損値のある行を落としてから10歳ごとにクラス分けをして、生存率を調べます。
# Ageの欠損値を除いたデータフレーム'age_data'を作成
data_age = data.dropna(subset=['Age']).copy()
# 10歳ごとに区分け
data_age['Age_bin'] = pd.cut(data_age['Age'],[i for i in range(0,81,10)])
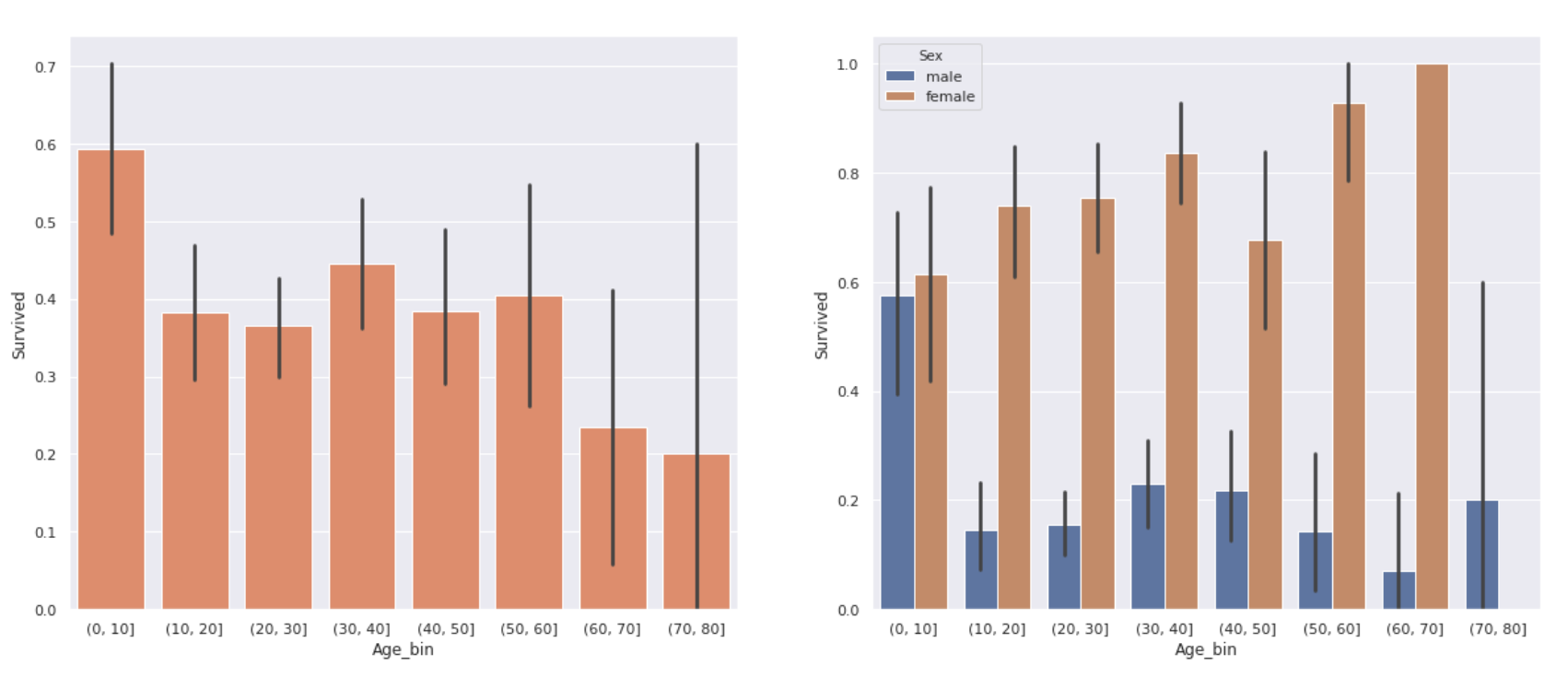
fig, ax = plt.subplots(1,2, figsize=(20,8))
sns.barplot(x='Age_bin', y='Survived', data=data_age, color='coral', ax=ax[0])
sns.barplot(x='Age_bin', y='Survived', data=data_age, hue='Sex', ax=ax[1])
右のグラフは左のグラフを男女別にしたものです。
年代によって生存率に違いがでました。10歳以下の子供の生存率は比較的高く、60歳以上の高齢者は生存率が20%程とかなり低いです。
また、10代〜50代の間での生存率に大きな差はありませんでした。
ただ、男女別に見てみると女性の場合は60歳以上の人でも生存率がかなり高くなっています。
左のグラフで高齢者の生存率が低かったのは60歳以上の女性の数が少なかった(3人のみ)ことも影響している可能性があります。
7. Embarked
乗客が乗船した港によって違いはあるのでしょうか。
plt.figure(figsize=(12,8))
sns.barplot(x='Embarked', y='Survived', data=data)
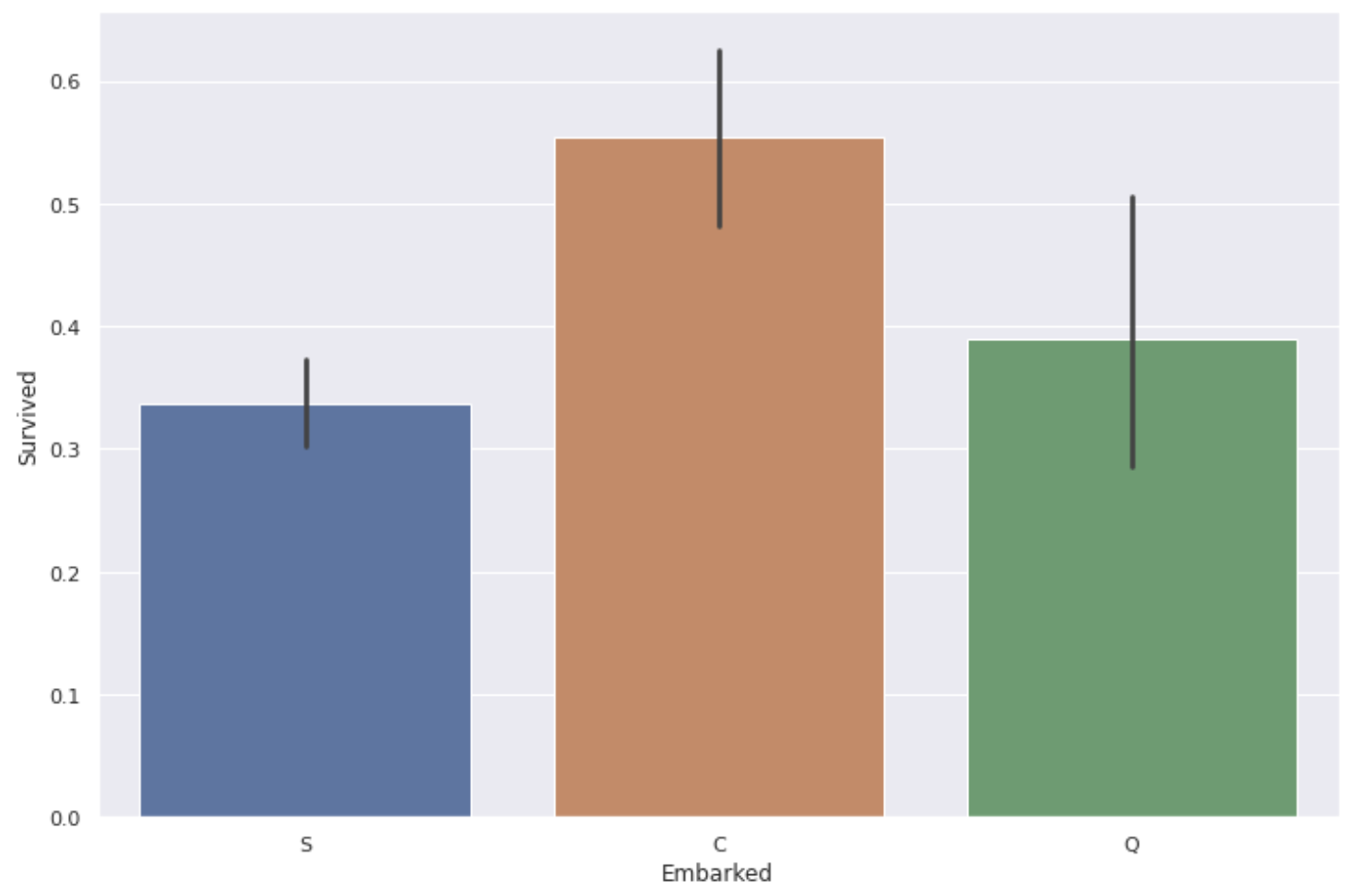
C(Cherbourg)の港から乗船した人の生存率が少し高いです。
港そのものが影響を与えているとは考えにくいので港の種類ごとのPclassとFareを見てみます。
fig, ax = plt.subplots(1,2, figsize=(12,8))
sns.countplot(data['Embarked'], hue= data['Pclass'], ax=ax[0])
sns.boxplot(x='Embarked', y='Fare', data=data, sym='', ax=ax[1])
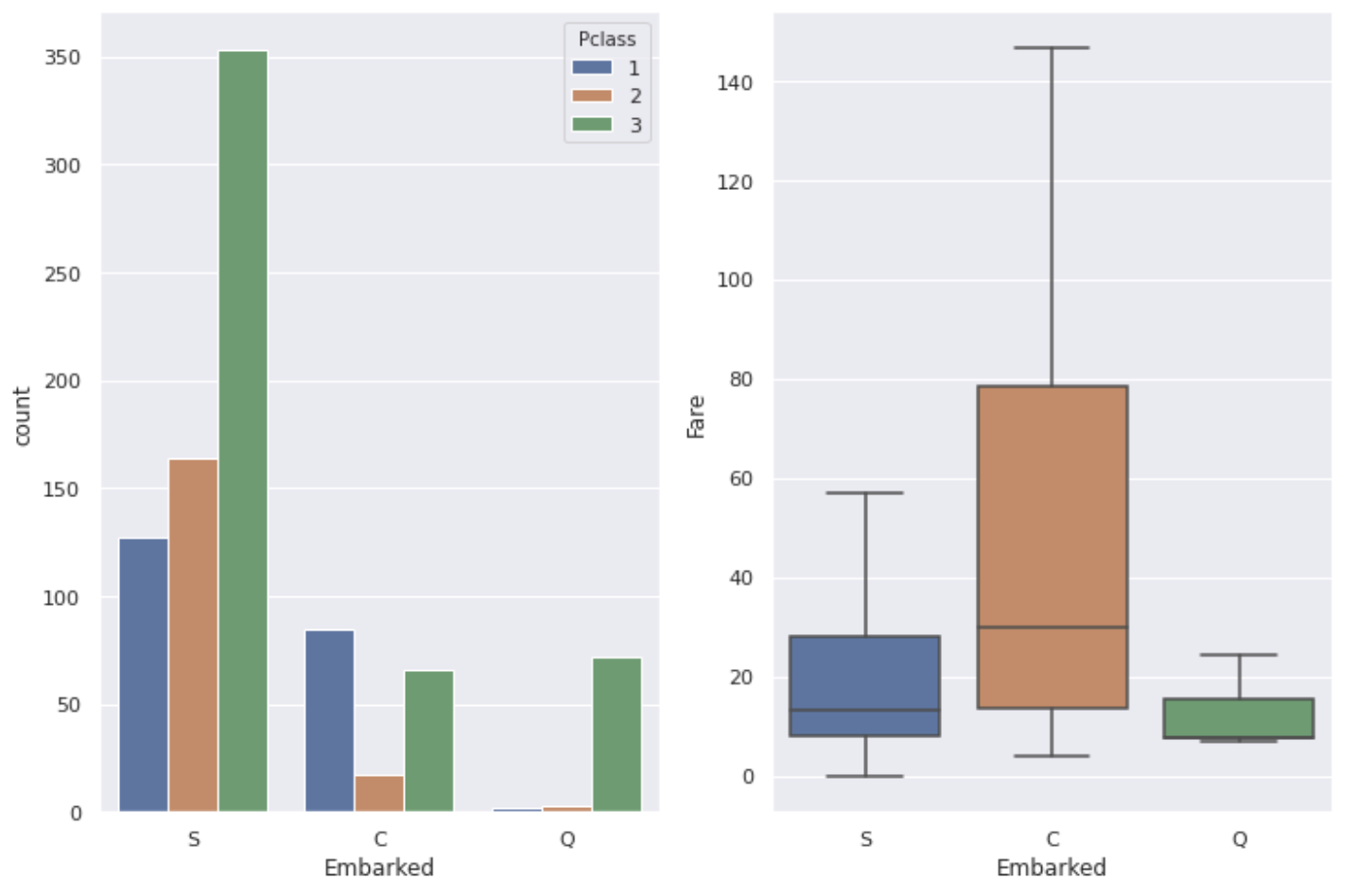
地域によってそこに住む人の階級や職業なども異なっていそうなので港によっても上のグラフのような差がでています。
全体を見るとS(Southampton)の港から乗った人がかなり多いようです。
Cの港での生存率が高かったのはPclass:1の人の割合が高く、Fareも比較的高いからだといえます。
Q(Queenstown)の港から乗ったほとんどの人はPclass:3なので生存率が一番低くてもよさそうなのですが実際はSの港での生存率が一番低くなっています。
SとQでそこまで大きな差があるわけではありませんがデータ数の違いもあるのでSの港から乗った人の生存率が一番低い理由は単に**「Pclass:3の人が多いから」**としか言いようがなさそうです。
8. Cabin
欠損値の割合が77%もあるので予測モデルに与える特徴量としては使うのは難しいですが記録されているデータを使ってなにか得れるものがないか調べてみます。
タイタニックの船の図面がこちらのサイトに載っていました。
Plans détaillés du Titanic
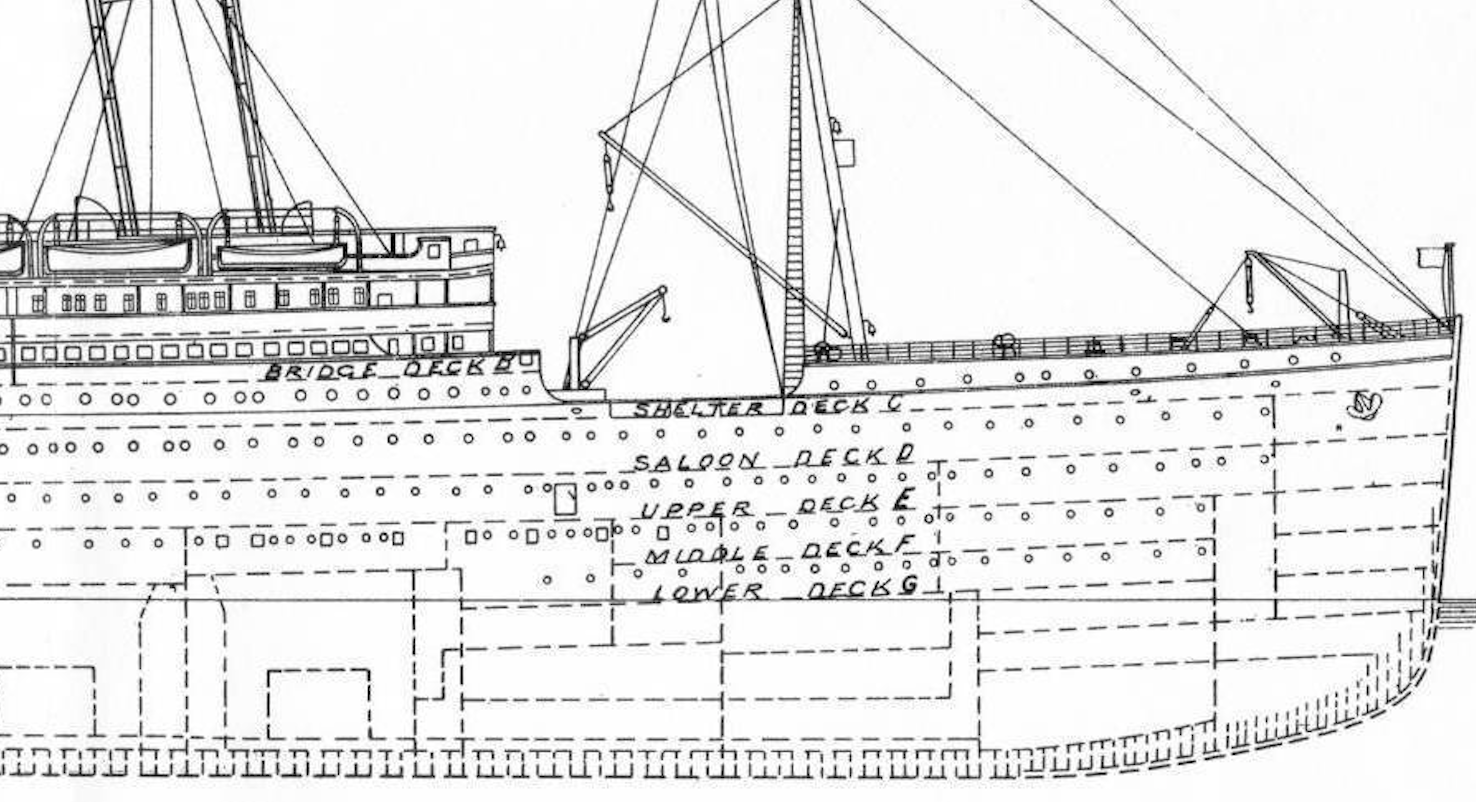
客室は「B96」のように表記されており先頭のアルファベットが客室の階層を表しています。
アルファベットはA~G,Tの種類があり、Aが船の一番上の階(豪華な部屋)、Gが一番下の階(普通の部屋)になっています。
救命ボートは上のデッキに置いてあること、船への浸水は下から始まることを考えると上のデッキに一番近いAの客室の人の生存率が高そうです。
実際のデータではどうなるか見てみます。
# Cabinのアルファベットだけを入れた'Cabin_alpha'の列を作成
# nは欠損値になっている行
data['Cabin_alpha'] = data['Cabin'].map(lambda x:str(x)[0])
data_cabin=data.sort_values('Cabin_alpha')
plt.figure(figsize=(12,8))
sns.barplot(x='Cabin_alpha', y='Survived', data=data_cabin)
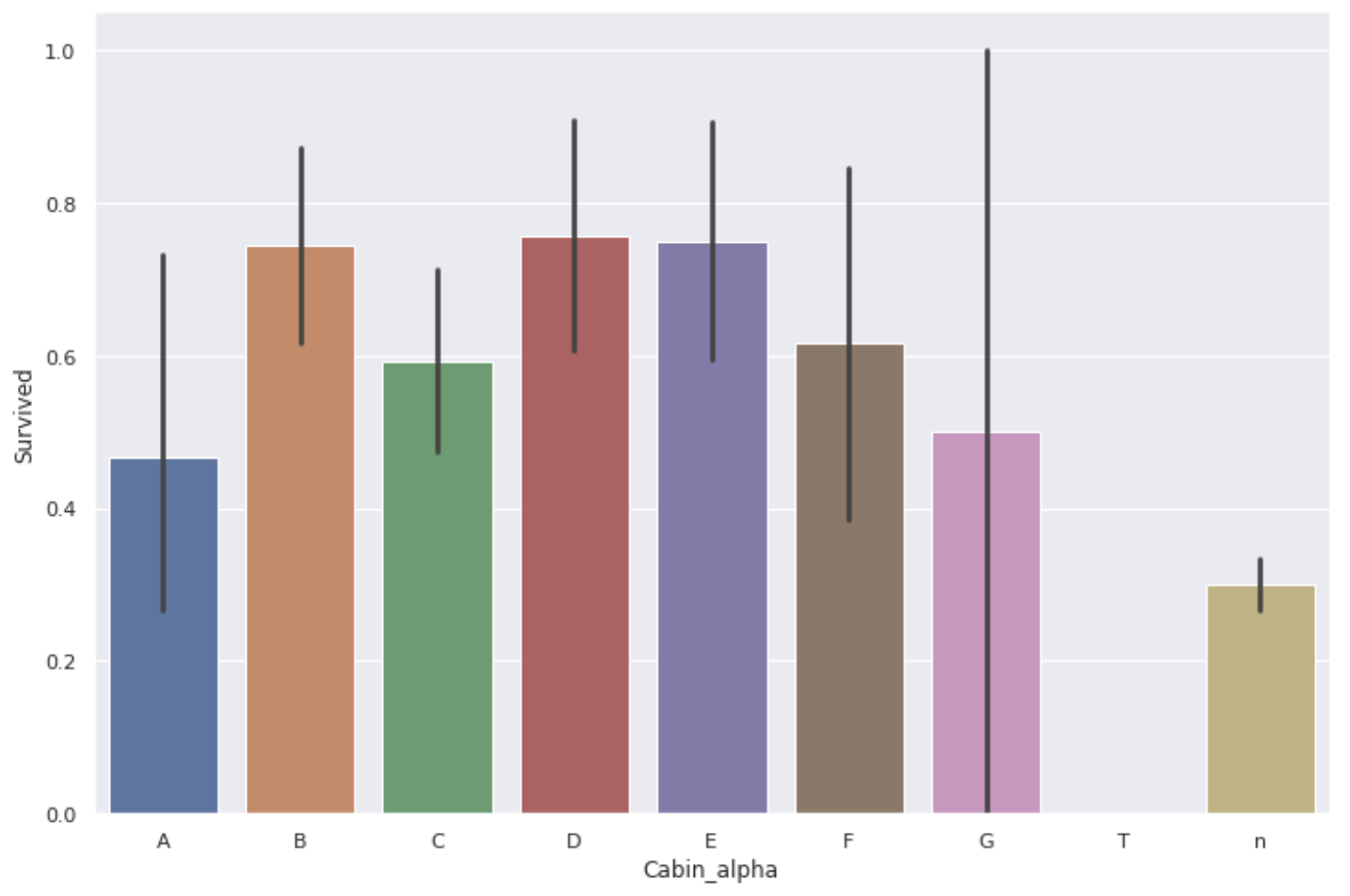
予想に反して、Aの客室の生存率はあまり高くありませんでした。
データの数も合わせてみてみると下の表のようになります。
data['Survived'].groupby(data['Cabin_alpha']).agg(['mean', 'count'])
| mean | count | |
|---|---|---|
| Cabin_alpha | ||
| A | 0.466667 | 15 |
| B | 0.744681 | 47 |
| C | 0.593220 | 59 |
| D | 0.757576 | 33 |
| E | 0.750000 | 32 |
| F | 0.615385 | 13 |
| G | 0.500000 | 4 |
| T | 0.000000 | 1 |
| n | 0.299854 | 687 |
B,Cのデータ量はまだマシかもしれませんが、A,Gのデータ量はかなり少ないので客室の階層によって生存率に違いがあったと言い切ることは出来ません。
また、チケットのときと同様に同じ客室番号の人がいたので「部屋が同じ」→「友人や家族で乗船」→「生存率に違いが出る」と思い、部屋番号が重複しているかどうかでそれぞれの生存率を求めました。
data['Cabin_count'] = data.groupby('Cabin')['PassengerId'].transform('count')
data.groupby('Cabin_count')['Survived'].mean()
| Cabin_count | 生存率 |
|---|---|
| 1 | 0.574257 |
| 2 | 0.776316 |
| 3 | 0.733333 |
| 4 | 0.666667 |
| 見た感じだと1人で部屋にいた人の生存率が少し低いかな...ぐらいの差しか得られませんでした。 | |
| やはりデータ数が少なすぎるのではっきりとした結果が出ません。 |
Cabinの列は逆に予測の妨げや過学習の原因になると割り切って切り捨ててしまってもいいかもしれません。
まとめ
今回は予測モデルに与える特徴量として使えそうなデータを見つけるためにSurvivedとの関係をメインにデータ分析をしてみました。
生存率に大きく関係していそうな特徴量はPclass、Fare、家族の人数(Family_size)、チケットの重複(Ticket_count)、性別、年齢ということがわかりました。
次回はtrainデータとtestデータに含まれる欠損値を補い、予測モデルに与えるデータフレームを完成させたいと思います。
ご意見、ご指摘などがございましたらコメントしていただけるとありがたいです。