kaggleのtitanic ニューラルネットを使った生存者予測 [80.4%]

前回は決定木ベースのxgboostを使って生存率を予測してみました。
前回：kaggleのtitanic xgboostを使った生存者予測 [80.1%]

今回はkaggleでもよく使われているNeuralNetworkを用いてタイタニックの生存者予測にチャレンジしてみます。

コードはGitHubでも公開しています。
neuralnetwork.py

1.　データの取得と欠損値の確認

import pandas as pd
import numpy as np
import os, random
import tensorflow as tf

#乱数を固定する関数
def reset_seed(seed):
    os.environ['PYTHONHASHSEED'] = '0'
    random.seed(seed) # random関数のシードを固定
    np.random.seed(seed) # numpyのシードを固定
    tf.random.set_seed(seed) # tensorflowのシードを固定

#乱数を固定
reset_seed(28)

train = pd.read_csv('/kaggle/input/titanic/train.csv')
test = pd.read_csv('/kaggle/input/titanic/test.csv')
#trainデータとtestデータを１つにまとめる
data = pd.concat([train,test]).reset_index(drop=True)
#欠損値が含まれる行数を確認
train.isnull().sum()
test.isnull().sum()

それぞれの欠損値の数は下のようになりました。

	trainデータ	testデータ
PassengerId	0	0
Survived	0
Pclass	0	0
Name	0	0
Sex	0	0
Age	177	86
SibSp	0	0
Parch	0	0
Ticket	0	0
Fare	0	1
Cabin	687	327
Embarked	2	0

2. 欠損値の補完と特徴量の作成

2.1 Fareの補完

欠損している行のPclassは3でEmbarkedはSでした。

この2つの条件を満たす人の中での中央値で補完します。

data['Fare'] = data['Fare'].fillna(data.query('Pclass==3 & Embarked=="S"')['Fare'].median())

2.2 グループごとの生死の違い'Family_survival'の作成

Titanic [0.82] - [0.83]こちらのコードで紹介されていた 'Family_survival' という特徴量を作成します。

家族や友人同士だと船内で行動を共にしている可能性が高いので生存できたかどうかもグループ内で同じ結果になりやすいといえます。

そこで名前の名字とチケット番号でグルーピングを行い、そのグループのメンバーが生存しているかどうかで値を決めます。

この特徴量を作成することで予測の正解率が2％ほど向上したのでこのグルーピングはかなり有効です。

#名前の名字を取得して'Last_name'に入れる
data['Last_name'] = data['Name'].apply(lambda x: x.split(",")[0])

data['Family_survival'] = 0.5 #デフォルトの値
#Last_nameとFareでグルーピング
for grp, grp_df in data.groupby(['Last_name', 'Fare']):

    if (len(grp_df) != 1):
        #(名字が同じ)かつ(Fareが同じ)人が2人以上いる場合
        for index, row in grp_df.iterrows():
            smax = grp_df.drop(index)['Survived'].max()
            smin = grp_df.drop(index)['Survived'].min()
            passID = row['PassengerId']

            if (smax == 1.0):
                data.loc[data['PassengerId'] == passID, 'Family_survival'] = 1
            elif (smin == 0.0):
                data.loc[data['PassengerId'] == passID, 'Family_survival'] = 0
            #グループ内の自身以外のメンバーについて
            #1人でも生存している → 1
            #生存者がいない(NaNも含む) → 0
            #全員NaN → 0.5

#チケット番号でグルーピング
for grp, grp_df in data.groupby('Ticket'):
    if (len(grp_df) != 1):
        #チケット番号が同じ人が2人以上いる場合
        #グループ内で1人でも生存者がいれば'Family_survival'を1にする
        for ind, row in grp_df.iterrows():
            if (row['Family_survival'] == 0) | (row['Family_survival']== 0.5):
                smax = grp_df.drop(ind)['Survived'].max()
                smin = grp_df.drop(ind)['Survived'].min()
                passID = row['PassengerId']
                if (smax == 1.0):
                    data.loc[data['PassengerId'] == passID, 'Family_survival'] = 1
                elif (smin == 0.0):
                    data.loc[data['PassengerId'] == passID, 'Family_survival'] = 0

2.3 家族の人数を表す特徴量 'Family_size' の作成と階級分け

SibSpとParchの値を使って何人家族でタイタニックに乗船したかという特徴量'Family_size'をつくり、その人数に応じて階級分けをします。

#Family_sizeの作成
data['Family_size'] = data['SibSp']+data['Parch']+1
#1, 2~4, 5~の3つに分ける
data['Family_size_bin'] = 0
data.loc[(data['Family_size']>=2) & (data['Family_size']<=4),'Family_size_bin'] = 1
data.loc[(data['Family_size']>=5) & (data['Family_size']<=7),'Family_size_bin'] = 2
data.loc[(data['Family_size']>=8),'Family_size_bin'] = 3

2.4 名前の敬称 'Title' の作成

Nameの列から'Mr','Miss'などの敬称を取得します。
数が少ない敬称('Mme','Mlle'など)は同じ意味を表す敬称に統合します。

#名前の敬称を取得して'Title'に入れる
data['Title'] = data['Name'].map(lambda x: x.split(', ')[1].split('. ')[0])
#数の少ない敬称を統合
data['Title'].replace(['Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Officer', inplace=True)
data['Title'].replace(['Don', 'Sir',  'the Countess', 'Lady', 'Dona'], 'Royalty', inplace=True)
data['Title'].replace(['Mme', 'Ms'], 'Mrs', inplace=True)
data['Title'].replace(['Mlle'], 'Miss', inplace=True)
data['Title'].replace(['Jonkheer'], 'Master', inplace=True)

2.5 Ageの補完と階級分け

Ageの欠損値の補完には名前の敬称ごとに求めた年齢の平均値を使用します。
そして子供(0~18)、成人(18~60)、高齢者(60~)の3つに階級分けします。

#敬称ごとの平均値でAgeの欠損値を補完
title_list = data['Title'].unique().tolist()
for t in title_list:
    index = data[data['Title']==t].index.values.tolist()
    age = data.iloc[index]['Age'].mean()
    age = np.round(age,1)
    data.iloc[index,5] = data.iloc[index,5].fillna(age)

#年齢ごとに階級分け
data['Age_bin'] = 0
data.loc[(data['Age']>18) & (data['Age']<=60),'Age_bin'] = 1
data.loc[(data['Age']>60),'Age_bin'] = 2

2.6 Fareの標準化&特徴量のダミー変数化

Fareの値は変数のスケール差が大きいので、ニューラルネットが学習しやすいように標準化(平均値が0、標準偏差を1にする)します。

そして文字列になっている列をget_dummiesでダミー変数化していきます。
Pclassは数値ですが値の大きさそのものに意味はないのでこちらもダミー変数に変換しておきましょう。

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
#Fareを標準化したものを'Fare_std'に入れる
data['Fare_std'] = sc.fit_transform(data[['Fare']])
#ダミー変数に変換
data['Sex'] = data['Sex'].map({'male':0, 'female':1})
data = pd.get_dummies(data=data, columns=['Title','Pclass','Family_survival'])

最後に不要な特徴量を落とします。

data = data.drop(['PassengerId','Name','Age','SibSp','Parch','Ticket',
                     'Fare','Cabin','Embarked','Family_size','Last_name'], axis=1)

データフレームはこのような形になりました。

	Survived	Sex	Family_size_bin	Age_bin	Fare_std	Title_Master	Title_Miss	Title_Mr	Title_Mrs	Title_Officer	Title_Royalty	Pclass_1	Pclass_2	Pclass_3	Family_survival_0.0	Family_survival_0.5	Family_survival_1.0
0	0.0	0	1	1	-0.503176	0	0	1	0	0	0	0	0	1	0	1	0
1	1.0	1	1	1	0.734809	0	0	0	1	0	0	1	0	0	0	1	0
2	1.0	1	0	1	-0.490126	0	1	0	0	0	0	0	0	1	0	1	0
3	1.0	1	1	1	0.383263	0	0	0	1	0	0	1	0	0	1	0	0
4	0.0	0	0	1	-0.487709	0	0	1	0	0	0	0	0	1	0	1	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
1304	NaN	0	0	1	-0.487709	0	0	1	0	0	0	0	0	1	0	1	0
1305	NaN	1	0	1	1.462069	0	0	0	0	0	1	1	0	0	0	0	1
1306	NaN	0	0	1	-0.503176	0	0	1	0	0	0	0	0	1	0	1	0
1307	NaN	0	0	1	-0.487709	0	0	1	0	0	0	0	0	1	0	1	0
1308	NaN	0	1	0	-0.211081	1	0	0	0	0	0	0	0	1	0	0	1

1309 rows × 17 columns

統合させていたデータをtrainデータとtestデータに分けて特徴量の処理は終了です。

model_train = data[:891]
model_test = data[891:]

x_train = model_train.drop('Survived', axis=1)
y_train = pd.DataFrame(model_train['Survived'])
x_test = model_test.drop('Survived', axis=1)

3. モデルの構築と予測

データフレームが完成したのでニューラルネットのモデルを構築し予測をさせてみます。

from keras.layers import Dense,Dropout
from keras.models import Sequential
from keras.callbacks import EarlyStopping
#モデルの初期化
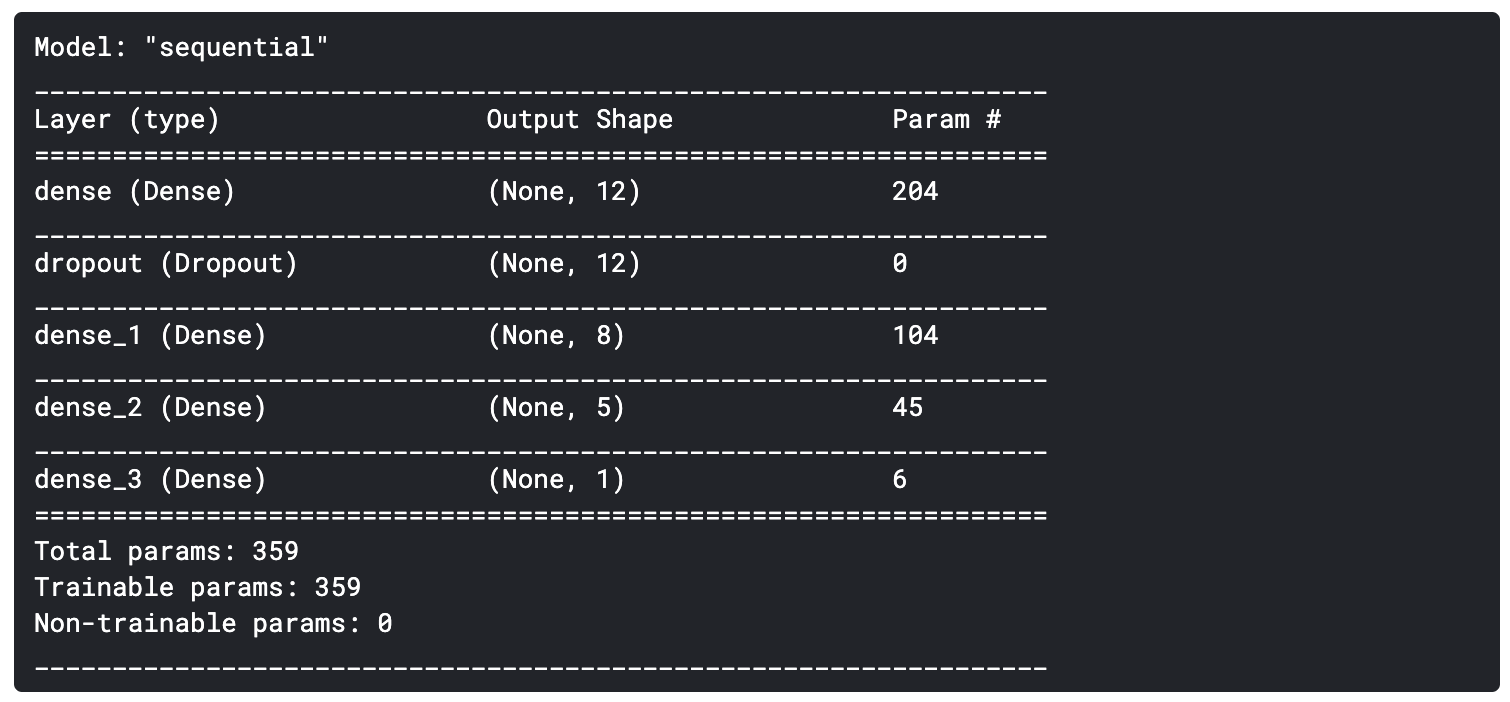
model = Sequential()
#層の構築
model.add(Dense(12, activation='relu', input_dim=16))
model.add(Dropout(0.2))
model.add(Dense(8, activation='relu'))
model.add(Dense(5, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
#モデルの構築
model.compile(optimizer = 'adam', loss='binary_crossentropy', metrics='acc')
#モデルの構造を表示
model.summary()

trainデータを渡して学習をさせます。
validation_splitを設定しておけばtrainデータの中からvalidation用のデータを勝手に分けてくれるので楽ですね。

log = model.fit(x_train, y_train, epochs=5000, batch_size=32,verbose=1,
                callbacks=[EarlyStopping(monitor='val_loss',min_delta=0,patience=100,verbose=1)],
                validation_split=0.3)

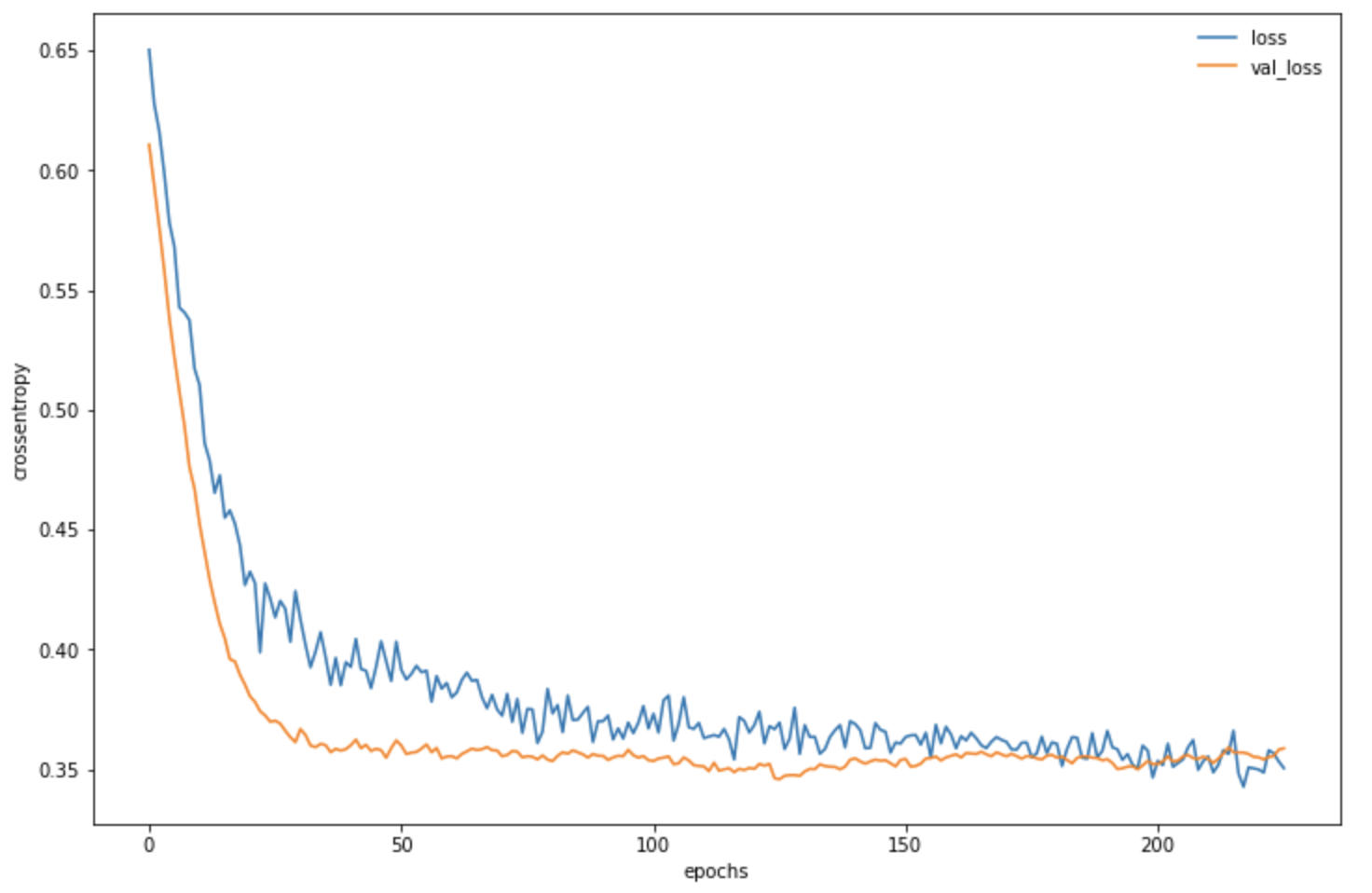
学習が進行する様子をグラフで表示させるとこのようになります。

import matplotlib.pyplot as plt
plt.plot(log.history['loss'],label='loss')
plt.plot(log.history['val_loss'],label='val_loss')
plt.legend(frameon=False)
plt.xlabel('epochs')
plt.ylabel('crossentropy')
plt.show()

最後にpredict_classesで予測値を出力させます。

#0と1どちらに分類されるかを予測
y_pred_cls = model.predict_classes(x_test)
#kaggleに出すデータフレームを作成
y_pred_cls = y_pred_cls.reshape(-1)
submission = pd.DataFrame({'PassengerId':test['PassengerId'], 'Survived':y_pred_cls})
submission.to_csv('titanic_nn.csv', index=False)

今回の予測モデルの正解率は80.4%でした。
ニューラルネットはパラメータやモデルの層の数などを自由に決めることができるので作成したこのモデルが最適かどうかはわかりませんが8割を超えればまずまずといったところでしょうか。

ご意見、ご指摘などがございましたらコメント、編集リクエストをしていただけるとありがたいです。

参考にさせていただいたサイト、書籍

ニューラルネットワークの実装（分類）
Titanic - Neural Networks [KERAS] - 81.8%
Titanic [0.82] - [0.83]
Kaggleで勝つデータ分析の技術
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装