はじめに
本記事では前回の記事の補足のおはなしです。
回帰を解く際におなじみの疑似逆行列について、重回帰分析を題材に幾何学的に考えていこうと思います。
重回帰分析とは
詳しくは前回の記事を参照ってことでところどころ省略していきます。別窓で開きながら読んでいただけると分かりやすいかもです。
問題設定
観測データとしてD次元のベクトルの入力$\mathbf{x}\in \mathbb{R}^D$と出力$y\in \mathbb{R}$のペア$\left\{(\mathbf{x}_n,y_n)\right\} _{n=1}^N $から$y=f(\bf{x})$となるような関数$f$を推定すること
$\newcommand{\argmax}{\mathop{\rm arg~max}\limits}$$\newcommand{\argmin}{\mathop{\rm arg~min}\limits}$
導出
$\mathbf{y}=(y_1,y_2,...,y_N)^T,\mathbf{X}=(\mathbf{x}_1,\mathbf{x}_2,...,\mathbf{x}_N)^T$とすると重回帰では以下のように最小二乗法によって
解$\mathbf{\hat{w}}$を求めます。
\begin{eqnarray}
\mathbf{\hat{w}}&=&\argmin_\mathbf{w}\|\mathbf{y}-\mathbf{X}\mathbf{w}\|^2
\end{eqnarray}
本題
この最小二乗法をデータ数$N$と次元数$D$に注目しながら深く考えていきます。
(1)$N=D$のとき
今回は幾何学的に考えるために$N=D=3$の時を想定します。
観測データの集合$\mathbf{y}$は下図(右)のように$y_1,y_2,y_3$によって張られる$N$次元空間に一点として表現されます。
この$\mathbf{y}$を$\mathbf{x}^{(d)}$を用いて以下の式のように表現することを考えます(重回帰で考えている式と変わりません)。
\begin{equation}
\mathbf{y}=w_1\mathbf{x}^{(1)}+w_2\mathbf{x}^{(2)}+w_3\mathbf{x}^{(3)} \tag{1}
\end{equation}
ちょっとややこしいので$\mathbf{x}^{(d)}$について追加説明すると
\mathbf{x}^{(d)}=(x^{(d)}_1,x^{(d)}_2,...,x^{(d)}_N)^T
であることに注意してください。
$\forall d \mathbf{x}^{(d)}\in\mathbb{R}^N,\mathbf{y}\in\mathbb{R}^N$の制限のもとに下図が描けます。
このとき$\mathbf{w}=(w_1,w_2,w_3)$も$D$次元空間上の一点として定まります。
式(1)を変形すると
\begin{equation}
\mathbf{y}=\mathbf{X}\mathbf{w} \tag{2}
\end{equation}
式(2)に両辺左から$\mathbf{X}^{-1}$をかけて($N=D$より$\mathbf{X}$はフルランク)
\begin{equation}
\mathbf{w}=\mathbf{X}^{-1}\mathbf{y} \tag{3}
\end{equation}
式(2),(3)、$\mathbf{y}$は$\mathbf{w}$に$\mathbf{X}$をかけることで、$\mathbf{y}$は$\mathbf{w}$に$\mathbf{X}^{-1}$をかけることで求まりますね。(下図の赤矢印)
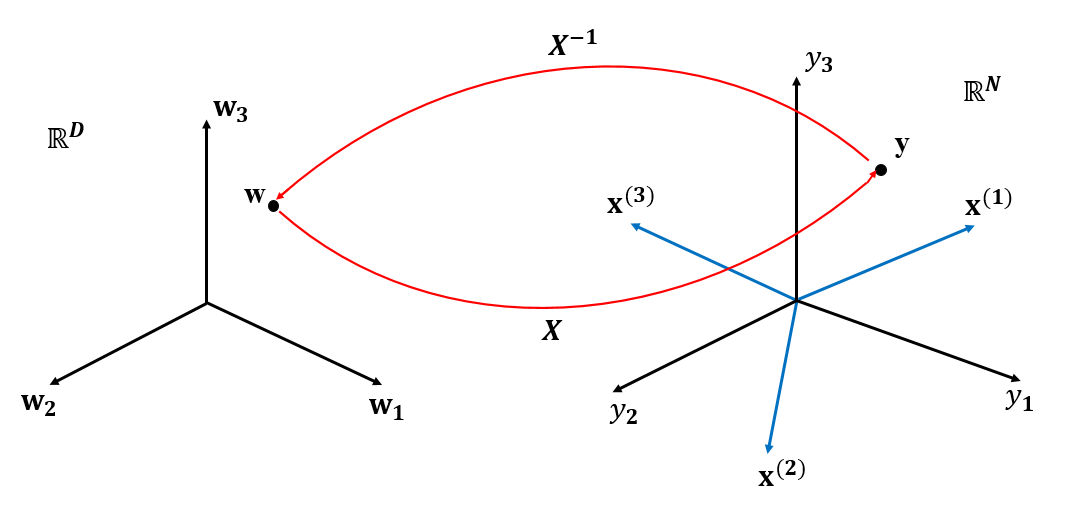
ただの逆行列でできちゃいましたね。
これはふつうに連立方程式を解いているのと変わりません。
かなり限定的な状況なのでもっと一般的な状況を考えていきましょう!
(2)$N>D$のとき
さっきと同様に幾何学的に考えるために$N=3,D=2$の時を想定します。
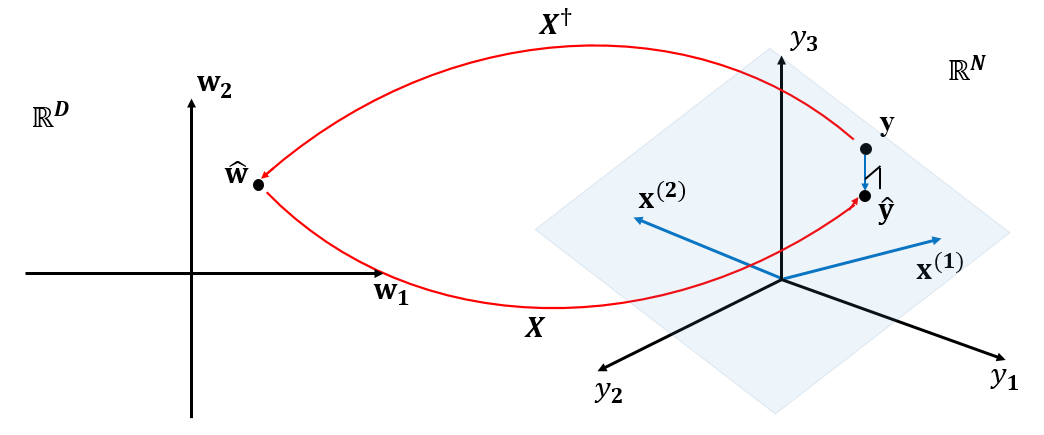
観測データの集合$\mathbf{y}$は下図(右)のように$y_1,y_2,y_3$によって張られる$N$次元空間に一点として表現されます。
この$\mathbf{y}$を$\mathbf{x}^{(d)}$を用いて表現したいのですが$\mathbf{x}^{(1)},\mathbf{x}^{(2)}$の張る$D$次元部分空間上(薄い青の部分ね)にこの$\mathbf{y}$は無い場合が多いでしょう。
なんとか表現するとすれば$\mathbf{y}$を部分空間に対して直交射影した$\mathbf{\hat{y}}$ですね。
この$\mathbf{\hat{y}}$を表現するような$\mathbf{w}$を$\mathbf{\hat{w}}$とすると、この$\mathbf{\hat{w}}$は最小二乗法を用いて求められます。
\begin{equation}
\mathbf{\hat{w}}=\argmin_\mathbf{w}\|\mathbf{y}-\mathbf{X}\mathbf{w}\|^2 \tag{4}
\end{equation}
回帰でおなじみの式が出てきましたね!
式(4)を解くと
\begin{equation}
\mathbf{\hat{w}}=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}
\end{equation}
\begin{equation}
\mathbf{\hat{y}}=\mathbf{X\hat{w}}
\end{equation}
$(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\equiv\mathbf{X}^{\dagger}$とおいたときの$\mathbf{X}^\dagger$をムーア-ペンローズの疑似逆行列とよびます。
$\mathbf{w}=\mathbf{X}^\dagger\mathbf{y},\mathbf{\hat{y}}=\mathbf{X\hat{w}}$の関係を表したものが下図の赤矢印です。
ここで$\mathbf{\hat{y}}$から$\mathbf{\hat{w}}$を考えてみましょう。疑似とはいえ仮にも逆行列と呼ばれるくらいです。$N=D$のときと同じ(式(3)のとこ)ようにできるかやってみましょう。
\begin{eqnarray}
\mathbf{X}^\dagger\mathbf{\hat{y}}&=&(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{\hat{w}}\\
&=&(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{X\hat{w}}\\
&=&\mathbf{\hat{w}}
\end{eqnarray}
出来ましたね!
$\mathbf{\hat{y}}$と$\mathbf{\hat{w}}$は$\mathbf{X}^\dagger$を逆行列のように用いることで行ったり来たりができることが分かりました!$\mathbf{y}$には戻せないんですね~
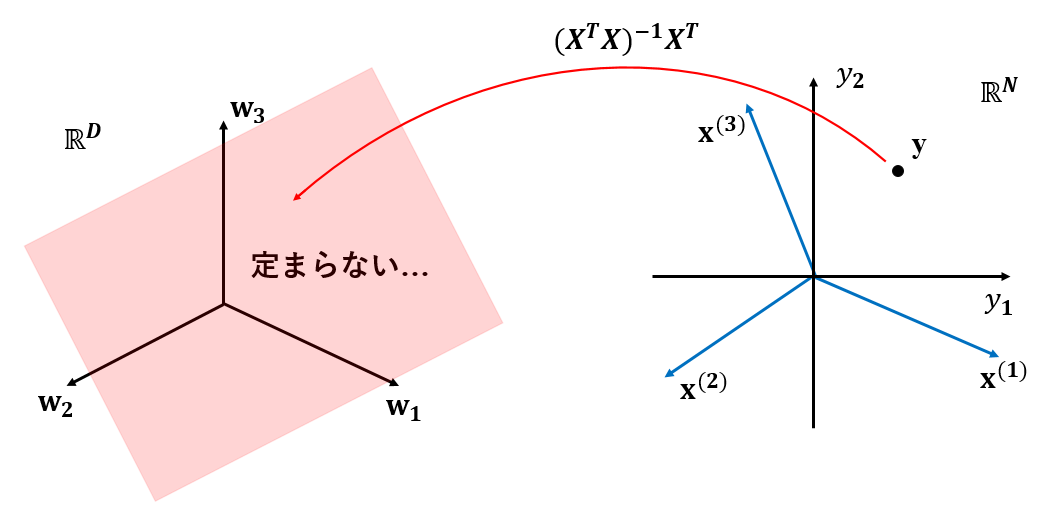
(3)$D>N$
おまけで$D>N$のときの図も書いてみましょう。(前回取り扱ったのはここですね)
例によって$N=2,D=3$の時を想定します。
$\mathbf{y}$を$\mathbf{x}^{(d)}$を用いて表現しようとすると、その$\mathbf{w}$は$N$次元部分空間上に分布することになり$\mathbf{w}$を定めることができません。
これは$\mathbf{X}^T\mathbf{X}$が非正則であるため$(\mathbf{X}^T\mathbf{X})^{-1}$が存在しないところから来ますが詳しいことは前回の記事を参照くださいm(_ _)m
まとめ
線形回帰における疑似逆行列がどんな風に最小二乗法と関わってくるかを、重回帰分析を題材に幾何学的に考えてみました。
線形回帰ってとっても単純な手法ですがよくよく見ると考えることがいっぱいですね…
参考文献
線形代数-基礎と応用 新井仁之 著