リアルタイムソルバーの技術的解説

これは ペンシルパズルI Advent Calendar 2021 の 17 日目の記事です。

はじめに

以前、Twitter でペンシルパズルのリアルタイムソルバー pzprRT というものを公開しました。

これは一言でいえば、問題を編集するとリアルタイムにその解答が表示されるという機能のついたパズル問題エディタです。

この記事では、pzprRT の内部で何が起こっているのかについて解説したいと思います。

大まかな構成

pzprRT は、すべてがクライアント側で動作するようになっています。これは次の理由によるものです：

• サーバーサイドで実行する場合、過負荷がかかるとレスポンスが悪くなる、現実的にはタイムアウトを設ける必要があるなどの問題がある。そのため、原理上解けるはずの問題が解けない、といった問題が生じる。
• サーバーサイドとのやり取りでどうしても遅延時間が生じる。
• サーバー側でソルバーを動作させるのはいろいろと面倒なのであまりやりたくない

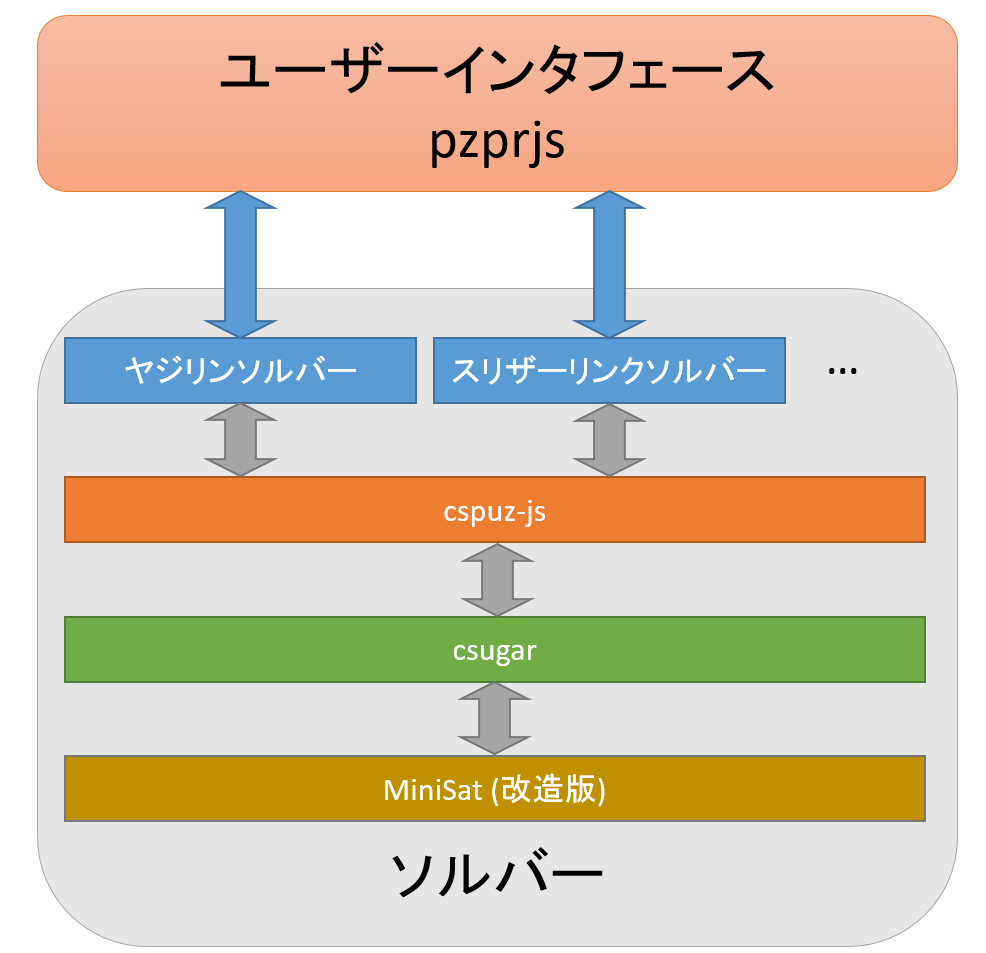
pzprRT の大まかな構成を示すと下図のようになります。

ユーザーインタフェース

pzprRT のユーザーインタフェースは、pzprjs をほぼそのまま用いています。これは、pzprjs を使用した puzz.link がインターネット上でパズル問題を出題するために頻繁に使用され、多くのユーザーにとって馴染みがあること、またインタフェース部を 1 から実装するのは手間が大きいから、という理由があります。

この部分については、現在編集中の問題をソルバー部に渡す機能、ソルバー部から返ってきた解答を適切に表示する機能などがあれば十分です。十分ソルバーが高速に解答を返してくることを前提として、問題が編集されるたびに同期的にソルバーを呼び出し、返ってきた解答を表示します。
どう pzprjs を改造したかの詳細については技術的に難しいところはないので省略しますが、実装は GitHub 上 にあるので、興味がある方はこちらをご参照ください。

ソルバー

リアルタイムソルバーでは、問題の変更があった際に十分高速に解を求める必要があります。ペンシルパズル百科の記事にある通り、すべての解を埋め込んでおくという方法もパズルによっては有効ですが、ほとんどのペンシルパズルではこれは使えません（例えば、Wikipedia によれば数独の解答盤面のパターン数は、対称性を加味しても数十億通りにもなり、これをすべて埋め込んだデータベースを持っておくのは非現実的です）。そのため、解のデータベースなどには依存せず速く解けるソルバーを作成する必要があります。pzprRT では、ベースとなる手法は制約充足問題 (CSP) 経由で充足可能性問題 (SAT) ソルバーを使用し、SAT ソルバーの高速性を活用するというものですが、更なる高速化のためにペンシルパズル頻出の制約（グラフ連結性）を SAT ソルバーで高速に扱えるようにする改造も実施しています。

---

ソルバー内部では、どのパズルも制約充足問題 (CSP) に帰着することで問題を解いています。CSP に帰着してからの自動解答はすべて同様のプロセスになります。

• MiniSat (改造版) ¹: C++ で記述された、充足可能性問題 (SAT) を解くソルバー (SAT ソルバー) です。ただし、SAT ソルバーそのままではパズルを解くためには性能として不十分なため、オリジナルの MiniSat に改造を施してあります (詳細は後述)。
• csugar: Java で記述された CSP ソルバー Sugar ² を、MiniSat 等 SAT ソルバーと密に連携できるように (パズルソルバーに必要な部分に限って) C++ に移植したものです。
• cspuz-js: パズルを CSP に変換するのは SAT に直接変換するのに比べれば容易ですが、それでも CSP の制約を直接 DSL で記述するのは面倒です。cspuz-js は TypeScript 上で CSP ソルバー (csugar) を扱いやすくするためのラッパーとして機能します。
• 各パズル (ヤジリン等) のソルバー: pzprjs から与えられたパズル問題を cspuz-js を用いて CSP 経由で解答します。

この説明でわかる通り、MiniSat および csugar は C++ で記述されているため、そのままではブラウザ上で動かすことができません。そのため、emscripten を使って WebAssembly に変換することで、ブラウザ上で動かせるようにしています。

理論的背景

充足可能性問題 (SAT) は、論理式が充足可能か、すなわち論理変数に適切に真偽を定めて、論理式全体を真とする方法が存在するかを判定する問題です。ここで、論理式としては節標準形 (CNF) のみを考えても表現能力は変わらないので、以後 CNF のみを考えることとします。
CNF は、いくつかの論理変数またはその否定を論理和（$\vee$, または）でつないだものを節として、いくつかの節の論理積（$\wedge$, かつ）の形で書ける論理式を言います。例えば $X, Y, Z$ を論理変数、$\bar{X}, \bar{Y}, \bar{Z}$ をそれぞれの否定とすれば、$(X \vee \bar{Y}) \wedge (\bar{X} \vee Z)$ は CNF です。この例の場合、例えば $X$ を真、$Y$ を偽、$Z$ を真とすれば式を充足することができます。

制約充足問題 (CSP) は、与えられた制約を充足する変数割当が存在するかを判定する問題です。制約というだけだとかなり範囲が広いですが、例えば「算術式の比較が真 (例えば $X + Y \geq 2$ など)」「与えられた値すべてが異なる (alldifferent)」といった条件を扱うことができます。

判定問題 (入力に対して、真か偽かの 2 値を返す問題) は、真となるような入力について、それが真である「証拠」を（決定性チューリングマシンで）多項式時間で検証可能ならば計算量クラス NP に属します。多くのペンシルパズルは、それを解の存在についての判定問題とみなしたとき、「証拠」として解を与えればそれが正しく解であるかどうかの検証は多項式時間であるから、NP に属します。NP に属する任意の問題がある問題に多項式時間帰着されるとき、その問題は NP 完全 であると言います。簡単にいうと、NP 完全問題が十分効率よく解けるなら、NP に属する多くのペンシルパズルも効率よく解けるだろう、ということになります（正確には、多項式時間だからといって現実的に効率よく解けるとは限りません。例えば入力サイズ $n$ に対して $n^{1000000}$ の時間で動作するアルゴリズムは、およそ現実には使い物にならないと考えられますが多項式時間です）。

SAT は、NP 完全であることが知られています³。つまり、多くのペンシルパズルは SAT に「効率よく」帰着することが可能です（実際には、多くのペンシルパズルは NP 完全であることも知られています ⁴）。ところが、実際にペンシルパズルを SAT に直接帰着するのは大変なため、今回は CSP に帰着してパズル問題を解くことにします（一般に SAT で表現できる制約は自明に CSP でも表現できるため、CSP も同様に NP 完全です）。

SAT ソルバー

SAT は代表的な NP 完全問題として知られていますが、NP 完全問題には恐らく多項式時間解法がないだろうと予測されています。それどころか、変数の数を $n$ としたとき、任意の $\epsilon > 0$ に対して、SAT を $O((2-\epsilon)^n)$ で解くアルゴリズムが存在しないだろうと予想されています (強指数時間仮説 (SETH))。つまり SAT は一般の場合にはまったく効率的には解けないだろうと予想されているのですが、それにも関わらず現代の SAT ソルバー は現実的な多くの入力に対して（変数の個数が 10 万オーダーのものも含めて！）実用的な時間で解を求めることができます。
ここでは、SAT ソルバーに使われている主なアルゴリズムについて簡単に説明します。

DPLL⁵ アルゴリズム

Davis–Putnam–Logemann–Loveland (DPLL) アルゴリズムは SAT を解くためのアルゴリズムの 1 つです。

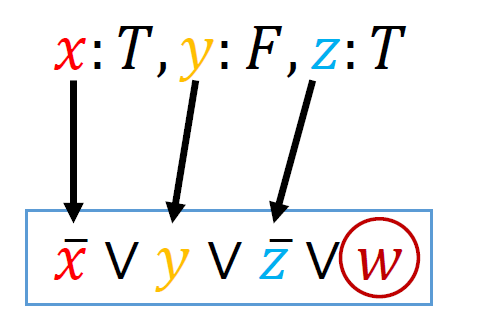
DPLL では、基本的には「未決定の変数を 1 つ選び、それを真とするか偽とするかの両方を探索する」ということを繰り返していきます。今まで決定した変数のみで矛盾（どうやっても真にできない節）が検出されたら探索はそこで打ち切りバックトラックします。さらに、1 つの未決定変数を除いたすべての項が偽になっているような節（例えば、$\bar{x} \vee y \vee \bar{z} \vee w$ で、$x$ が真、$y$ が偽、$z$ が真の場合）では、この未決定変数（ここでは $w$）は真とするほかありませんが、次探索する変数を選ぶ前に、このように自動的に決定できる変数を決めるということも行います (propagation)。propagation の過程で決まった変数がさらに他の変数を決める、ということが連鎖的に起きることもあります。

Wikipedia によれば、オリジナルの DPLL では純リテラル規則と呼ばれる規則もあるようですが、実際の実装では省略されることもあるようです（例えば MiniSat には含まれていなかったはずです）。

CDCL⁶ アルゴリズム

Conflict-driven clause learning (CDCL) アルゴリズムも SAT を解くためのアルゴリズムです。

CDCL では、DPLL に加えて節学習というものを行います。この節学習は、探索の過程で矛盾を検出した際に、その矛盾が起きた理由を解析し、その理由に対応する節を SAT の節集合の中に追加する、というものです。

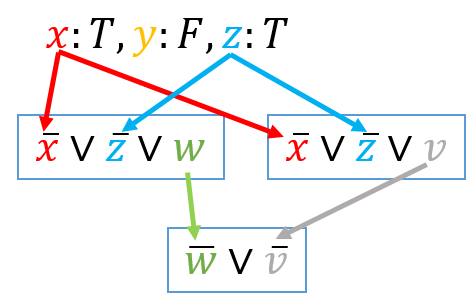
例えば上図において、$x$ を真、$y$ を偽、$z$ を真と（この順に）決めた段階で、propagation によって $\bar{x} \vee \bar{z} \vee w$ を介して $w$ が真であることが、$\bar{x} \vee \bar{z} \vee v$ を介して $v$ が真であることが決まり、ここから $\bar{w} \vee \bar{v}$ で矛盾が導かれます。どうしてこの節で矛盾が起こったかを、propagation での依存関係を見ながら解析すると、$x$ と $z$ がともに真であることが原因であることがわかります（$y$ は $w$, $v$ の導出には一切関わっていません）。よって、$\bar{x} \vee \bar{z}$ でなければならないことがわかり、以後この節も含めて探索を行って良いことがわかります。また、$\bar{x} \vee \bar{z}$ から、最後に決めた $z$ が真であるというのはただちに否定されることになります。学習した節次第では、最後に決めた変数値どころか、さらに前の変数割当を否定するべき可能性もあり、この場合は大きくバックトラックを行うことができます (backjumping)。

MiniSat¹ のアルゴリズムは CDCL に基づいていますが、他にも分岐する変数の選択のヒューリスティクスなどの工夫も含まれています。

SAT ソルバーを使用した CSP ソルバー

ここでは、論理変数に加えて、有限の値域内に値が含まれるような整数変数も扱えるような CSP ソルバーを考えます。

複雑な式であっても、論理変数のみが現れる論理式であれば、Tseitin transformation を用いることで CNF に変換することができます。一方、整数変数が現れる制約を SAT に帰着するには、整数変数に対する制約も論理変数のみを用いて表現する必要があります。⁷では、いくつかの表現方法が挙げられています。ここでは、値として $X_1 < X_2 < \dots < X_n$ のいずれかをとりうる整数変数 $X$ の表現を考えます。

• 直接符号化: $X=X_1, X=X_2, \dots, X=X_n$ に対応する論理変数を導入する。
• 順序符号化: $X \leq X_1, X \leq X_2, \dots, X \leq X_{n-1}$ に対応する論理変数を導入する。$X \leq X_n$ は常に成り立つことから、これに対応する変数はわざわざ導入する必要がない。
• 対数符号化: $X$ を $2$ 進法で表記したときの各位に対応する論理変数を導入する。

Sugar、およびそれを移植した csugar では順序符号化を用いています。

パズルの CSP への帰着

基本的には、パズルの解答要素に対応する変数をそれぞれ導入し、パズルのルールを 1 つずつこの変数上の制約として記述していきます。

例えば、簡単な例としてナンバープレイスを考えます。ナンバープレイスのルールは

• $9 \times 9$ の盤面の各マスに 1～9 の整数を入れる。
• 各行、各列、各 $3 \times 3$ のブロックには、1～9 の整数が 1 つずつ入るようにする。

というものです。

まず、1 つ目のルールから、上から $y$ マス目、左から $x$ マス目に入る整数に対応する変数 $A_{y,x} \in \{1, 2, \dots, 9\}$ を導入します。
次に、2 つ目のルールから、同じ行、列、ないしブロックに含まれる 2 マスの組 $A_{y,x}$, $A_{y', x'}$ すべてについて、$A_{y,x} \neq A_{y', x'}$ という制約を追加します。例えば、$A_{1,1}$ と $A_{2,2}$ は同じブロックであることから、$A_{1,1} \neq A_{2,2}$ という制約が含まれます。
最後に、最初から書いてあるヒントに対する条件を追加します。例えば上から $2$ マス目、左から $3$ マス目に $7$ というヒントが書いてある場合には、$A_{2,3} = 7$ とします。
これらの制約をすべて加えて CSP ソルバーに解かせると、ナンバープレイスの解を求めることができます。

ところで、ペンシルパズルでは「～～がひとつながりになっている」といった制約が現れることがよくあります。ニコリのページを見ると、例えばぬりかべでは「すべての黒マスが縦横にひとつながりとなる」ルールがあり、へやわけでは「黒マスが盤面を分断してはいけない」すなわち「白マスが縦横にひとつながりとなる」ルールがあります。このような制約を CSP で表現するのは一見不可能なように見えますが、CSP は NP 完全ですから、表現する方法は存在します。ここではSugar 作者によるペンシルパズルの CSP 定式化をもとに、このような連結条件の表現について説明します。

マスが全部で $N$ 個あるとして、各マス $i$ に対して、そのマスが白マスであるとき真であるような論理変数 $A_i$ があるとして、白マスが盤面全体でひとつながりであるという制約を加えるとします。ここで、各マス $i$ に対し、$0$ 以上 $N-1$ 以下の整数値をとる整数変数 $R_i$ を割り当てます。これを便宜上ランクと呼ぶことにします。ランクについて、次のような制約を課すことにします。

• ランク $0$ の白マスが全体でただ 1 つ存在する。
• ランクが $0$ でない白マスについては、それに隣接する白マスであって、ランクがそれよりも小さいようなものが少なくとも 1 つ存在する。

このようなランクの割り当て方が存在することと、白マスが盤面全体でひとつながりであることは同値です。

証明

まず、白マスが盤面全体でひとつながりであるときは、白マス $i$ を任意に 1 つ選び、そのランクを $0$ とする。それ以外の白マスのランクは、$i$ までの最短路の長さ (隣り合うマスに移動して $i$ に到達することを考えた時、移動回数として考えられる最小のもの) とすると、上の制約を満たすことは明らか。

一方、このようなランクの割り当て方が存在するときは、ランク $0$ の白マスを $r$ として、任意の白マス $i$ から $r$ に白マスのみをたどって移動することができることを示せばよい。このためには、今いる白マスから、よりランクが小さい白マスに移動することを繰り返せばよい。ランクが $0$ でない白マスについてはこのような移動が常に可能で、移動のたびにランクが $1$ 以上減少することから、高々 $N-1$ 回の移動で $r$ に移動することが可能である。

---

最後に、この制約を CSP で記述する方法について述べます。$\mathbb{ite}(c, t, f)$ を、論理値 $c$ が真のときは整数値 $t$ を、偽のときは整数値 $f$ をとる関数とします（Sugar ではこれを制約の中に含めて書くことができます）。

• ランク $0$ の白マスが全体でただ 1 つ存在する。
  • $\sum_{i} \mathbb{ite}(R_i = 0 \wedge A_i, 1, 0) = 1$
• ランクが $0$ でない白マスについては、それに隣接する白マスであって、ランクがそれよりも小さいようなものが少なくとも 1 つ存在する。
  • $\forall_i, ((A_i \wedge R_i > 0) \Rightarrow \exists_{j \in {\cal N}(i)} A_j \wedge R_j < R_i) $
  • ${\cal N}(i)$ は $i$ に隣接するマスの集合

パズル問題を「解けるところまで」解く

SAT/CSP ソルバーは、基本的には解の発見 (あるいは解がないことの発見) に特化しています。つまり、パズル問題を CSP ソルバーに解かせると、そのままではとりあえず 1 つ答えを返して終わり、ということになってしまいます。
一方で、パズル作問のツールとして用いるためには、解を 1 つ見つけるだけでは十分で、それ以外に解がないか (唯一解であるか) の検証ができる必要があります。また、リアルタイムに解が表示されるということを踏まえると、表示される解は「現在の問題から論理的に導出される結果をすべて示している」ことが望ましいです。

すなわち、リアルタイムソルバーは「現在の問題に対する、正しい解答すべてに共通する解答要素（ある位置に線を引くか否か、など）」返す必要があります。
これを形式的に書くと次のようになります。

パズル問題 $P$ に対し、その問題の解答要素の集合を $E(P)$ とする。$P$ に対する解答 $a$ は $E(P)$ の部分集合で表される。$P$ の解答すべての集合を $A(P) \subseteq 2^{E(P)}$ で表すとき、リアルタイムソルバーは $\cap_{a \in A(P)} a$ を返すべきである。

CSP ソルバーが解を 1 つ見つけるというのは、$A(P)$ の元を 1 つ返すというのと等価です。これだけでは $\cap_{a \in A(P)} a$ を求めることはできませんが、一般に $E(P)$ 上の制約は CSP で容易に記述できるため、$e \subseteq E(P)$ に対して $C(e) = \left\{ a \in A(P) \mid e \not\subseteq a \right\}$ としたとき、$A(P) \cap C(e_1) \cap \ldots \cap C(e_k)$ の元を 1 つ見つける (つまり、解答要素集合 $e$ を完全には含まないような解を見つける) ことは容易です。これを踏まえると、$\cap_{a \in A(P)} a$ を見つけるアルゴリズムとして次のようなものが考えられます。

1. CSP ソルバーを用いて、$e \in A(P)$ を 1 つ見つける。見つからなければ $P$ に解はないことを報告して終了する。
2. CSP ソルバーを用いて、$a \in A(P) \cap C(e)$ を 1 つ見つける。見つかったなら、$e \leftarrow a \cap e$ として、2. の最初に戻る。見つからなかったなら、現在の $e$ が $\cap_{a \in A(P)} a$ である。

感覚的には、とりあえず 1 つ解を見つけて、その後は「すべての解に含まれる解答要素」の集合を順次削っていくようなイメージです。

ここで、2. の $i$ 回目の繰り返しでの $e$ を $e_i$ とすると、$e_1 \supseteq e_2 \supseteq \dots$ が成り立ちます。よって、$A(P) \cap C(e_i)$ は $A(P) \cap C(e_1) \cap \dots \cap C(e_i)$ とも表すことができます。この変形は一見何も意味がないように見えますが、これは「$i$ 回目に解く際には、前回 CSP ソルバーに与えた制約に $C(e_i)$ に対応する制約を加えて解を求めれば良い」ということを意味しています。CSP ソルバーでは（少なくとも Sugar では）解を求めた後さらに制約を追加して解を求める場合、前回の求解の際の探索結果（例えば CDCL における学習節）を活用して探索を行うことができるため、毎回新たなソルバーのインスタンスを作成して解を求めるよりも効率よく解を求めることができます。

停止性及び正当性の証明

CSP ソルバーの実行が停止することは前提とする。2. の各繰り返しにおいて、解が見つかったなら $e \not\subseteq e'$ より $e' \cap e \subsetneq e$ であるから、$|e|$ は単調に減少する。$e \subseteq E(P)$ かつ $E(P)$ は有限集合であり、$e = \emptyset$ の時 $A(P) \cap C(e) = \emptyset$ であるから、2. の繰り返しは高々 $|E(P)|+1$ 回で終了する。

次に正当性を証明する。$A(P) = \emptyset$ の場合は明らか。$A(P) \neq \emptyset$ ならば、このアルゴリズムで得られた集合を $e^\star$ とする。2. で解が見つからなくなるまでの繰り返し回数が $k$ 回であるとき、$a_0$ を 1. で見つけた解、$a_1, \ldots, a_{k-1}$ を 2. の $1, \ldots, k-1$ 回目の繰り返しで見つけた解とすると、$e^\star = a_0 \cap \dots \cap a_{k-1}$ となり、$a_i$ はいずれも $A(P)$ の元だから、$\cap_{a \in A(P)} a \subseteq e^\star$ は明らか。また、$A(P) \cap C(e^\star) = \emptyset$ より、任意の $a \in A(P)$ は $e^\star \subseteq a$ を満たすから、$e^\star \subseteq \cap_{a \in A(P)} a$ である。よって $\cap_{a \in A(P)} a = e^\star$ が示された。

なぜ SAT ソルバー (MiniSat) に改造が必要か

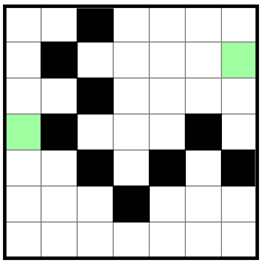
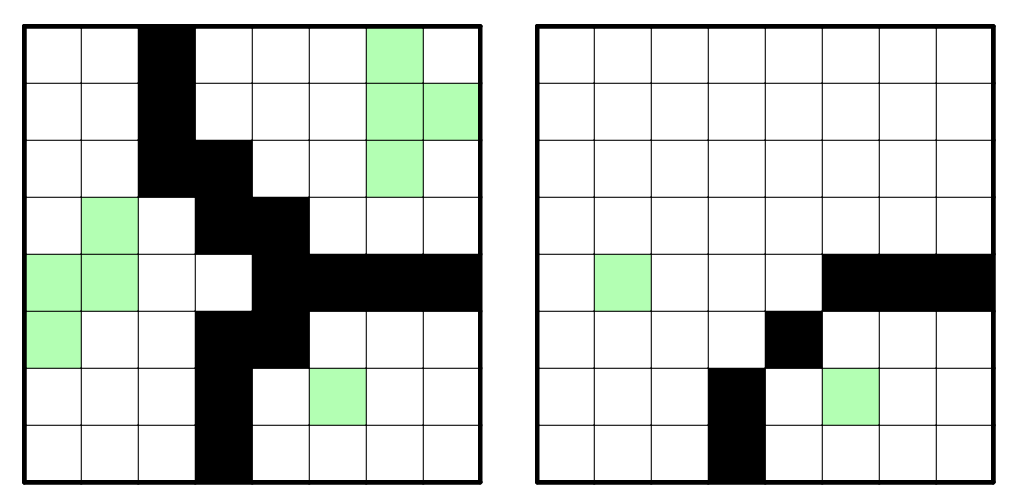
上のほうで「白マスがひとつながりになっている」といった制約を記述するための方法について説明しました。この方法で確かに連結制約を正しく記述することはできています。しかし、これだと大域的な分断が発生しても、それを直接検出することができないという問題があります（証明はしていませんが、実際に動かしてみると問題によっては極めて長い時間がかかります）。例えば、下図で白マス（未決定マス）をどう緑ないし黒で塗ったとしても、緑マスを縦横にひとつながりにすることは明らかに不可能ですが、直ちに矛盾を導くことは不可能です。

その他にも、連結制約を記述するために $N$（$N$ はマス数）通りの値をとる変数を各マスごとに導入する必要があり、CSP のレベルではまだしも SAT に帰着した段階でかなり変数が増えてしまうという問題があります（Sugar で使われている order encoding の場合、この制約を記述するためだけに $\Theta(N^2)$ 個）。

一方で、MiniSat のアルゴリズムの基礎となっている CDCL では、原理的には論理節以外の制約も追加することができます¹。例えば⁸では、有向グラフにサイクルが含まれないという制約を直接扱えるように SAT ソルバーを拡張しています。そのためには、各制約だけを取り出したときに「現在の変数割当から直ちに決まる変数の検出」と「ここで直ちに決まる変数が、どの変数割当から導出されるかの解析」が行えれば良いです。

ところが、かつての MiniSat ではこのような特殊制約の追加が容易だったものの、現在のバージョンでは（恐らく高速化のため）特殊制約の追加ができなくなってしまっています。そこで、グラフ制約の追加の前に、まず MiniSat に特殊制約のための対応を復活させる必要がありました。

こうすることで、連結制約を直接 SAT ソルバーに組み込むための準備が整いました。実際のアルゴリズムについては次節で解説します。

連結条件に対する推論

「ひとつながり」とか「隣り合うマス」とかいう言葉を使うのにも疲れてきました。ここからはグラフ理論の言葉を使うことにします。「マス」は以下頂点と同義とし、隣接するマス同士は対応する頂点同士が辺で結ばれていることとします。

先に示した図のように、白の頂点の塗り方によらず明らかに緑の頂点全体を連結にする（より正確には、緑の頂点からなる誘導部分グラフを連結にする）ことが不可能なケースでは、そのことを指摘できる必要があります。
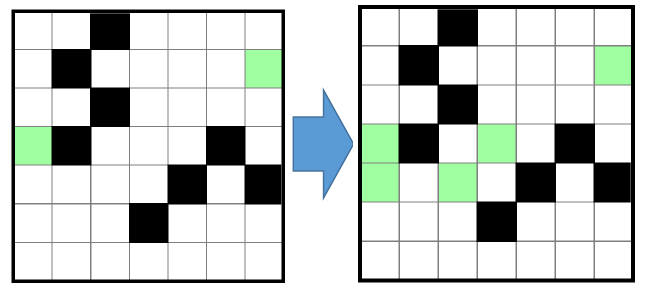
ところで、DPLL のアルゴリズムを思い出すと、現時点の変数割当から直ちに決定する変数についても指摘する、という手続き (propagation) があるのでした。グラフ連結条件についてもこれに対応したいと思います。例を挙げると、下図の左のような状況では、緑の頂点全体を連結にするために、右のように新たに 3 つの頂点が緑に確定することになります。

（正確には、propagation の実装がいい加減で、本来決まる頂点を指摘できなかったとしても、矛盾判定が正しくなされていれば問題なく動作はします。一方、正しく propagation を行ったほうが性能は向上します。当然のことながら、間違った頂点に対する指摘をしてしまうと、探索結果が間違ってしまうのでいけません。）

この推論について考える前に、最初に不可能なケースについて考えます。グラフを白の頂点と緑の頂点からなる連結成分に分解したときに、緑の頂点を含むような連結成分が複数存在するなら明らかに不可能です。一方、そのような連結成分がちょうど 1 個だけ存在するなら、その連結成分の白の頂点はすべて緑で、他の連結成分の白の頂点はすべて黒で塗ることで、緑の頂点を連結にすることができます。緑の頂点が存在しない場合についても（最後まで緑の頂点が一切存在しない場合を不可能としない限り）可能です。

よって、深さ優先探索を行うことで、現在の変数割当から直ちに不可能となるか、は $O(N+M)$ で（$N$ を頂点数、$M$ を辺の数とします）判定することができます。同様に、propagation の処理も、各（現在白で塗られた）頂点について緑および黒に置き換えた上で不可能性を判定する、ということを行えば、$O(N^2 + NM)$ で実行することは可能です。しかし、計算量的に明らかに不利です。実は、この処理は $O(N+M)$ で（オーダーとしては、不可能性判定を 1 回行うのと同じ時間で！）実行することが可能です。

まず、頂点を緑に塗ると不可能になる場合（必ず黒に塗らないといけない場合）について考えます。これは、（白と緑からなる）連結成分が複数存在し、他の連結成分にすでに緑の頂点が存在する場合に限られることがわかります。
次に、頂点を黒に塗ると不可能になる場合について考えます。ある頂点 $v$ を黒に塗るというのは、白と緑の頂点のみからなるグラフから $v$ を取り除くことに相当します。$v$ を取り除いた後で、緑の頂点を含むような連結成分が複数個存在するかどうか判定できればよいです。

このために、関節点を求めるアルゴリズムを応用することができます。関節点とは、無向グラフにおいて、それを取り除くとグラフが非連結となるような頂点のことを言います。関節点を求める際に、DFS 木を作った上で lowlink という値を求めるという手法がよく用いられますが、lowlink を用いると「ある頂点が関節点か」に加えて、「その頂点を取り除いた際、それに隣接する頂点たちのどれとどれが同じ連結成分に含まれるか」という情報も知ることができます。よって、DFS 木で各頂点を根とする部分木に含まれる緑の頂点の数を持っておけば、頂点 $v$ を取り除いた際、緑の頂点を含む連結成分が何個になるかは $O(|{\cal N}(v)|)$ で求めることができ、ゆえにグラフ全体での propagation の操作は $O(N+M)$ で行うことができます。

関節点の求め方についてはインターネット上に多数の資料があるのでここでは省略しますが、参考となるものをいくつか挙げておきます。

• アルゴリズムロジック: グラフにおける関節点(Articulation Points)を検出するアルゴリズム
• ACPC 2017 Day2 J: Cluster Network 解説

さて、次は CDCL のアルゴリズムを思い出しましょう。
CDCL では、矛盾（連結条件の場合、緑の頂点を連結にするのが不可能であることが判明した場合）が発生した際にその矛盾の理由を解析するために、各 propagation で決定された変数がどういう理由で決まったかというのを知る必要があります。論理節の場合は明らかで、例えば $x \vee \bar{y} \vee z$ という節から $z$ が真であることが決まるのは、$x$ が偽かつ $y$ が真の場合に決まっているのですが、グラフの連結条件についてはそれほど明らかではありません。自明な方法としては、その propagation が発生した際にすでに決定していた変数すべてを「理由」として返す、という方法がありますが、これだと「理由」が冗長になりがちです。例えば、下図の左側のマス目は矛盾となるケースですが、ここに含まれている緑頂点、黒頂点をすべて「理由」に含める必要はなく、右側のように削減しても問題ないことがわかります。

このように「理由」を削減するためのアルゴリズムについて考えます。考えるべきこととしては、矛盾が発生した理由、propagation が発生した理由、の 2 つがあるのですが、どちらもほぼ同じなので前者についてのみここでは述べます。削減の基準としては、「その変数の決定を理由から削減すると、適切な理由にならない（不可能性が言えなくなる）」というのが望ましいです。つまり、「理由」の集合として極小のものをとるということになります。このために、次のような貪欲法アルゴリズムを使うことができます。

• 「理由」を計算したい時点において、すでに行われた変数割当を適当な順に $D_1, D_2, \dots, D_k$ とする。
• $i=1, 2, \dots, k$ の順に、次を試す：
  • 現在の「理由」から $D_i$ を除去しても適切な「理由」になっているなら除去する。さもなくば、除去しない。

（ここで、$D_1, \dots, D_k$ の定め方は「適当な順」としましたが、実際には変数割当が決定したのが遅い順、としています。こうすることで、backjumping でできるだけ遠くまでバックトラックできるようになることが期待できます）

これは素直に実装すると、$D_i$ を除去して「理由」になっているかの判定が $O(N+M)$ のため、やはり $O(N^2 + NM)$ ですが、これも高速化することができます。そのためには、「緑の頂点の決定の除去: 連結成分内の緑の頂点数を 1 減らす」と「黒の頂点の決定の除去: （白および緑からなるグラフで）新たな頂点を作成し、隣接すつ白/緑の頂点と同じ連結成分に含める」ということが高速にできればよく、これは Union Find を用いると効率よく行うことができます。
ただし、今回は頂点の除去が失敗した場合には除去に伴う連結成分等の変化を巻き戻す必要があります。通常 Union Find で削除操作はできないのですが、今回の場合は「最後に操作を行う直前」に戻せれば十分なので、Union Find の情報を格納している配列に対する操作を記録しておけば、巻き戻しも変更と同じ計算量で行うことができます。よって、全体の計算量は $O((N + M)\log N)$ となります。
（$\log N$ は Union Find の操作のオーバーヘッドとなります。ここで、Union Find の計算量は $O(\alpha(N))$ （$\alpha$ は Ackermann 関数の逆関数）では？と思った方もいるかもしれませんが、これは巻き戻しなどを行わない場合のならし計算量になります。今回は巻き戻しが発生するため、簡単に証明できる範囲では union by rank を用いた最悪計算量の $O(\log N)$ で見積もるのが適切です。）

まとめ

リアルタイムソルバー pzprRT の設計についてまとめると次のようになります：

• リアルタイムソルバーは、どんなパズルも制約充足問題 (CSP) に帰着することで解いている
• 解答の高速化のために、充足可能性問題 (SAT) ソルバーを改造し、ペンシルパズルに頻出の制約を効率よく扱えるようにしている
• この改造では、競技プログラミング的なアルゴリズムを活用することにより、計算量の削減を図っている

1. Eén N., Sörensson N. (2004) An Extensible SAT-solver. In: Giunchiglia E., Tacchella A. (eds) Theory and Applications of Satisfiability Testing. SAT 2003. Lecture Notes in Computer Science, vol 2919. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-24605-3_37 ↩ ↩² ↩³

2. Naoyuki Tamura, Akiko Taga, Satoshi Kitagawa, Mutsunori Banbara: Compiling Finite Linear CSP into SAT, Constraints, Volume 14, Number 2, pp.254–272, June, 2009. DOI 10.1007/s10601-008-9061-0 ↩

3. Stephen A. Cook. 1971. The complexity of theorem-proving procedures. In Proceedings of the third annual ACM symposium on Theory of computing (STOC '71). Association for Computing Machinery, New York, NY, USA, 151–158. DOI:https://doi.org/10.1145/800157.805047 ↩

4. 八登 崇之. スリザーリンクのNP完全性について. 情報処理学会研究報告. AL, アルゴリズム研究会報告 74, 25-31, 2000-09-21. 一般社団法人情報処理学会 ↩

5. Martin Davis, George Logemann, and Donald Loveland. 1962. A machine program for theorem-proving. Commun. ACM 5, 7 (July 1962), 394–397. DOI:https://doi.org/10.1145/368273.368557 ↩

6. João P. Marques Silva and Karem A. Sakallah. 1997. GRASP—a new search algorithm for satisfiability. In Proceedings of the 1996 IEEE/ACM international conference on Computer-aided design (ICCAD '96). IEEE Computer Society, USA, 220–227. ↩

7. 丹生 智也, 田村 直之 , 番原 睦則 (2013). 位取り記数法に基づく整数有限領域上の制約充足問題のコンパクトかつ効率的な SAT 符号化. コンピュータソフトウェア, 30(1):211–230. DOI:https://doi.org/10.11309/jssst.30.1_211 ↩

8. Gebser M., Janhunen T., Rintanen J. (2014) SAT Modulo Graphs: Acyclicity. In: Fermé E., Leite J. (eds) Logics in Artificial Intelligence. JELIA 2014. Lecture Notes in Computer Science, vol 8761. Springer, Cham. https://doi.org/10.1007/978-3-319-11558-0_10 ↩