本稿では,動作計画の基礎知識と現場で実用化されている手法について解説していきます.ここで言う動作計画とは,障害物の回避をしながらロボットアームの手先を目標の位置・姿勢に到達させるまでの動作(関節軌道)を自動で生成することを指します.その手法にはRRTやRRT*, PRM, A*, CHOMP, STOMPなどが知られており,これらの派生形も次々と出版され続けています.
そんな中,私も2年ほど前に動作計画の論文を投稿してみました.
https://www.jstage.jst.go.jp/article/jrsj/40/2/40_40_154/_article/-char/ja/
自分で言うのも恐縮ですが,この手法は評判が良く,民間企業のエンジニアからも「これまでに調査した手法の中で最も有用な手法」という評価や「弊社の製品(コントローラ)に採用した」という報告も受けています.
ということで,本稿の後半では「この手法がなぜ実用化されるに至ったのか」についても説明していきます.また,論文の中では書けなかったことも本ブログに書き残しておきます.
関節空間上の経路計画問題への変換
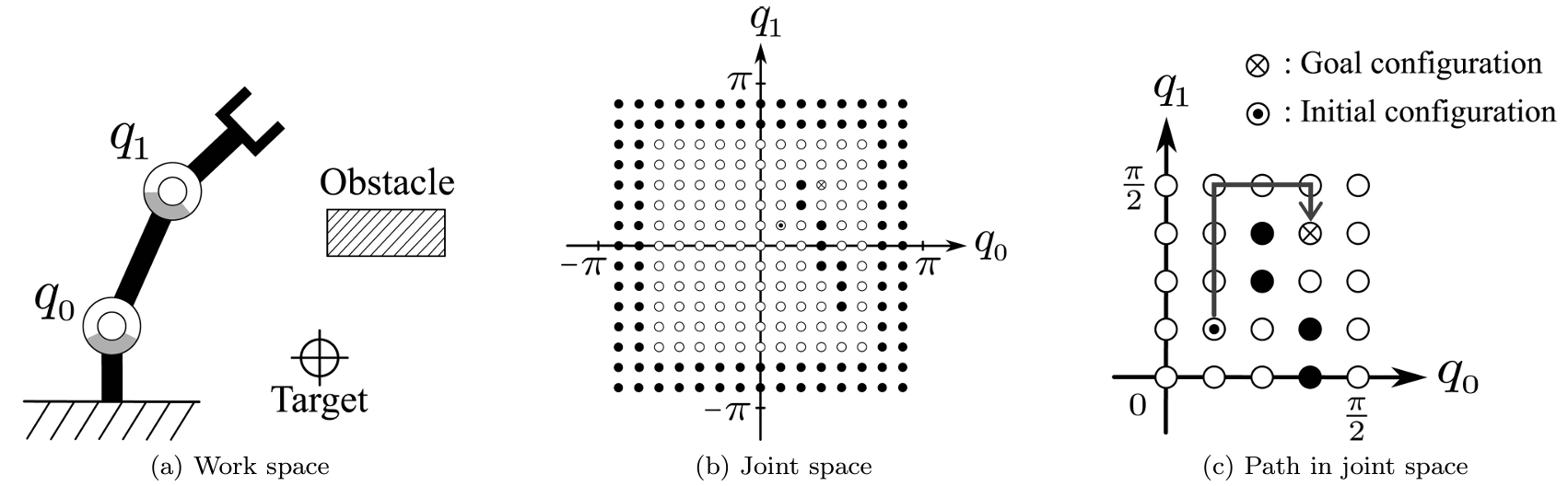
まず基礎知識として,ロボットアームの動作計画問題は,関節空間上の経路計画問題に変換できることを説明しておきます.下図の(a)が作業空間,(b)が離散的に表された関節空間,(c)が始点と終点を結ぶ経路です.
実際のロボットアームは作業空間上に存在しているのに対し,関節空間は物理的には存在しておらず,計算機の内部で仮想的に作られている空間です.関節空間の各座標軸はアームの各関節角度となっており,ロボットの自由度を$n$とすると,関節空間の次元も$n$となります.すなわち,関節空間上の点はロボットアーム全体の姿勢(各関節変位)に対応しており,関節空間は6次元などの高次元な空間(人間が直感的に想像できない空間)になります.関節空間上において,ロボットが障害物と干渉する点の集合を干渉領域(黒い点で表示)とし,そうでない点の集合を自由領域(白い点で表示)とします.関節空間上の自由領域内で始点(初期姿勢)と終点(手先が目標値と一致する姿勢=逆運動学解)を結ぶような経路を生成できれば,動作計画問題の解が得られます.ちなみに,前述した関節空間の図には私からの隠しメッセージが込められています.実は始点と終点を結ぶ経路を下図の赤線のようにすると,斜め移動をしている箇所でロボットと障害物は衝突します.

すなわち,関節角度の分割数が足りないことによって,本来は通れないはずの場所が通れてしまうという問題を象徴した図にしていました.つまり,この図は「関節空間を粗く離散化して大雑把に経路を作成し,後から細かい補正を行うという戦略は通用しない」ということを示唆しています(本当は論文内で明確に説明するつもりでしたが,話の流れ的に書くタイミングがなかった).また,関節空間を全て計算しようとすると,計算量やメモリ容量が容易に発散することも注意しなければなりません.例えば,各関節の角度を10等分することで離散的に関節空間を表した場合でも,関節空間上の点は$10^n$個になります.それぞれの点を干渉領域と自由領域に分類するためには,当然ながらロボットと障害物の干渉チェックを$10^n$回実行する必要があり,その後にも経路計画の計算が待っています.上記の性質により,2~3次元空間上の経路計画ではA*などが有用とされているのに対して,ロボットアームの動作計画ではRRTやその派生形が用いられる傾向があります.A*では最短経路を求められるという性質がありますが,最初から最短経路を求めようとすると計算量的に実行不可能となることが多いので,最初はRRTで大雑把に経路を求めて,後から経路に補正を行うという戦略が採用される傾向にあります(RRTでは「関節空間を粗く離散化」しているのではなく,「細かく離散化された関節空間上で経路を大雑把に生成」している点に注意されたい).
ちなみに,上記のような動作計画問題の解法はロボット工学の基礎知識となるはずですが,なぜか教科書には載ってないことがほとんどです.
RRTの原理と問題点
RRTでは関節空間上の始点から木が成長するように枝を追加していきます.ロボットアームの初期姿勢が点$\boldsymbol{q}_{\rm init}$で,終点(逆運動学解)が点$\boldsymbol{q}_{\rm goal}$に対応します.まず,ランダムに点$\boldsymbol{q}_{\rm rand}$を生成し,始点から点$\boldsymbol{q}_{\rm rand}$に向かって枝を生成します.ただし,枝の長さは最大で step size とします(RRTの論文に従って step size という言い方にしたが,$l_{\rm max}$とかの方が良いかも).

2本目以降の枝は,ランダムな点$\boldsymbol{q}_{\rm rand}$と最も距離が近い点に接続します.

もし枝上の点でロボットと障害物が干渉した場合は,その枝の追加を取り消します.すなわち,新たに枝を追加する度に干渉チェックが必要となります.黒い四角形が干渉領域であるならば,例えば下図の赤い枝は削除されることになります.

枝の追加を繰り返し行うと枝の先が終点の近くに到達するので,枝の先と終点を接続して計算を終了します.終点から逆に枝を辿ることで,下図の青線のような経路が得られます.

RRTの特徴はネットで調べれば色々と出てくるので,ここでは他の記事には書かれていない問題点だけを指摘しておきます.計算量やメモリ容量が無限にあると仮定すれば,RRTで始点と終点を結ぶ経路を必ず生成できます.しかし,実際にRRTを実行するとデッドロック(計算時間とメモリの消費量だけが増え続け,解に到達できない状態)に陥ることがあります.例えば,枝が下図のように成長した場合はデッドロックになります.

始点から成長した木が終点に到達するためには,図の赤い点で示した位置に向かって新たな枝を生成する必要がありますが,赤い点に最も近い点は,障害物(壁)の裏側にある点です.よって,壁の内側(始点側)で枝が増え続け,終点に向かって伸びる枝は成長しないという状態(デッドロック)に陥ります.ちなみに,この問題は始点と終点の両方から探索木を生成するBidirectional-RRT(Bi-RRT)に拡張すれば解決すると思われるかもしれませんが,少なくとも私の経験上では有力な解決策にはならなかったです.より正確には,Bi-RRTにすることでデッドロックに陥る頻度は低下したものの,相変わらずデッドロックになることはありました.このデッドロックの問題は簡単な実験をしただけでは発見が困難なこともあり,「RRTを使えば必ず解を求められる」という誤解をしている人も多いように見受けられますが,それは理論上(計算時間とメモリが無限のとき)の話であることに注意しなければなりません.
RRT*やRRT-Connectの説明もしようと思っていましたが,図を作るのが疲れたので割愛します.ここまで関節空間やRRTの説明をしておいてなんですが,次章で述べる方法は関節空間やランダムサンプリング,評価関数(最適化)といった類のものは一切使用しません.
実際に現場で採用された手法
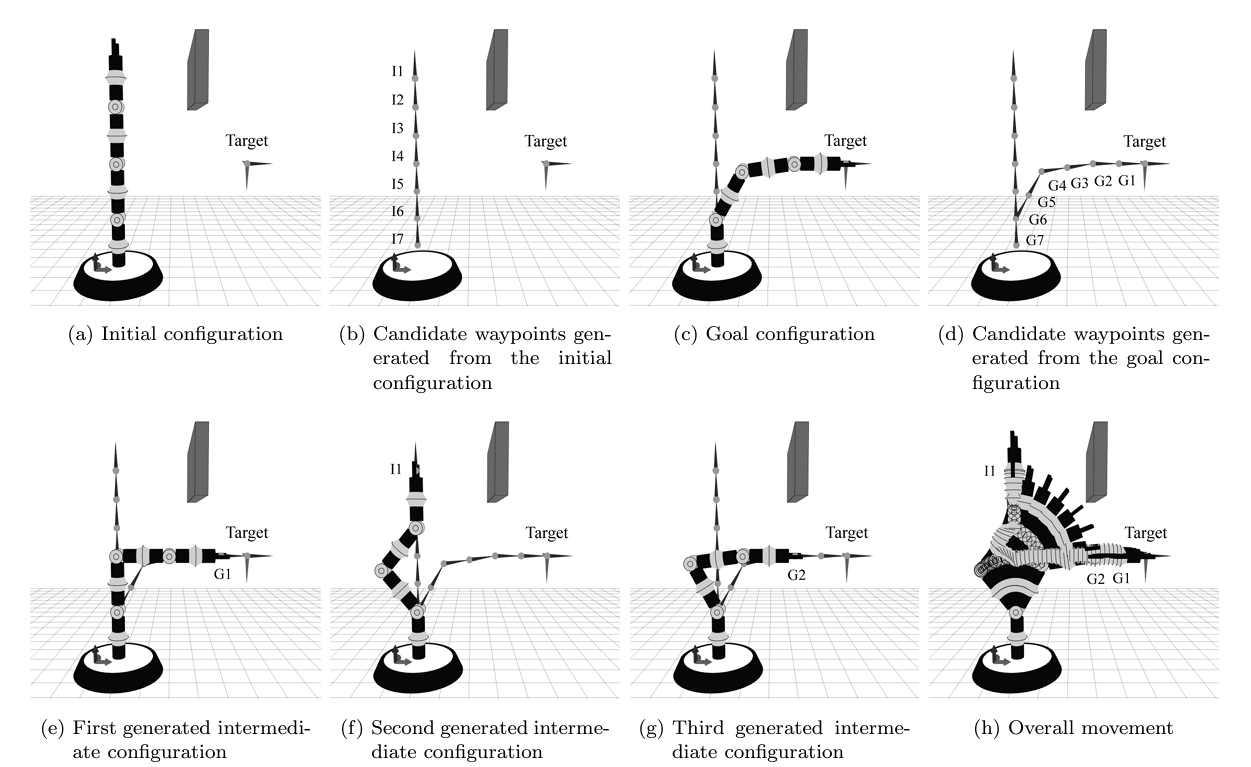
本章では,トレース動作を用いた方法について説明していきます.この方法の基本原理は極めて単純なものです.以下にトレース動作の説明図を記載します.
トレース動作を一言で説明すると「始点(初期姿勢)と終点(逆運動学解)におけるロボット自身の身体を手先がなぞる(トレースする)ように動作する」ということです.最初は手先を少しだけ引っ込めるような動作を生成し,その動作で障害物と干渉した場合は,さらに手先を根本側に引っ込めるように修正していきます.最終的には,上図の(a)→(f)→(g)→(e) →(c)の順でロボットの状態が変化し,手先が目標の位置・姿勢に到達します.また,トレース動作は以下の性質を動作計画に応用したものと解釈できます.
- ロボットの身体が元々存在していた場所には,障害物が無いことが確定している.
- ロボットアームの形状は直鎖状であるため,始点と終点のロボットの形状を結合すれば,手先と目標位置を繋ぐ1本の経路が必ず作成可能.
トレース動作の細かな手順については論文を参照していただくとして,ここでは「この手法がなぜ最も有用とされたのか」について整理していきます.トレース動作の利点は以下の通りです.
- 逆運動学を数回解いて,その結果を繋ぎ合わせるだけなので,計算量が少ない(RRTよりも少ない)
- 計算結果が乱数に依存しない.
- 原理が単純であり,なおかつ計算手順と計算結果の因果関係が明確であるため,改良やメンテナンスが簡単.
- 逆運動学を解く際に目標の手先姿勢を変更することで,動作途中の手先姿勢を指定できる(ピック&プレース作業に応用できる).
- 他の手法では解けない問題(狭い道を通る必要がある場合)でも解ける.
- ロボットが認識できていない(シミュレータ上に反映されていない)障害物があった場合でも,その障害物と干渉するリスクが低い(論文内では形跡領域を用いて定量的に評価している).
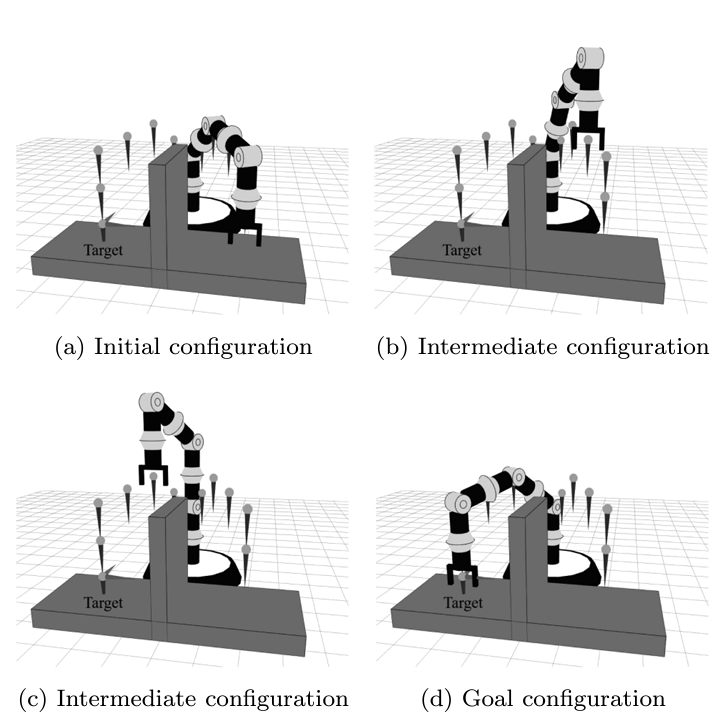
以降では,上記の4, 5, 6について補足していきます.まず,ロボットアームが実際に行う作業の多くはピック&プレース作業(箱や容器を持ち上げて,置く)の繰り返しになります.よって,「障害物の回避ができたとしても,その過程で手先の姿勢が横向きになっては困る」という場面は多いはずです.この点を踏まえると,上記4の性質は有用性に大きく貢献したと考えられます.例えば,動作途中の手先姿勢を常に真下を向く方向に指定することも可能です.手先に与える目標の位置・姿勢のうち,姿勢を下向きに設定して動作計画をしたときの結果を下図に示します.
次に,狭い道を通る必要がある動作計画問題としては,例えば以下のような事例が挙げられます.

このように障害物を配置した場合,関節空間上で経路計画をする際にも小さな穴を通り抜ける必要があるため,解くことが困難となります.実際に私が試行錯誤をした限りでは,どの従来手法を使っても解くことができませんでした.しかし,提案手法なら解くことが可能であり,実際に得られた動作のストロボ写真を以下に記載します.

個人的には,経路計画の文脈では未解決(or 難問)とされてきた「小さな穴を通り抜ける」という問題をシレっと解決している点が推しポイントです.
最後に,「そもそもロボットが認識できていない障害物をどのように避けるか」については,私の知る限りでは,従来研究で具体的な解決策を提示しているものはありませんでした.しかし,トレース動作では「元々ロボット自身が存在していた場所(障害物が無いことが確定している場所)をなぞるように動く」という原理を取り入れることで,認識できていない障害物と干渉するリスクも低減できています.例えば,下図の動作は従来手法(Bi-RRT + Path Pruning)で求めたものですが,関節空間上での経路長は短いものの,作業空間上では机(右下の物体)の上をなぎ払うような動きになっています.つまり,机上の物体まで細かくシミュレータに反映させておかないと,ロボットは障害物と衝突することになります.

一方で,提案手法では下図のような動作が得られます.

なお,冗長自由度を活用して肘と障害物の干渉を回避する機能(シフト動作)については,論文の方をご覧ください.
査読の裏話
既にお察しの方もいるかもしれませんが,この手法を発表すると賛成(アクセプト)派と反対(リジェクト)派に意見が分かれることが多いです.反対派が現れるのも無理はなく,従来研究では当たり前のように重視されてきた「解が求められることの数学的証明」や「評価関数の最適化」を全くしていないからです.具体的には,「解こうとしている問題が数式として書かれていないため,何を解決しているのかが分からない」や「何を最適化しているのかを数式で表し,結果を数値で示すべき」というのが反対派の意見です.しかし,今の動作計画に必要なのは証明や最適化ではなく,まずは現実的に意味のある解(結果が乱数に依存しないことや,ピック&プレース作業に適用できる結果)を出力できるようになることだと私は考えています.実際に現場では「現存する手法の中で最も有用な手法」として採用されていますし,この論文は従来研究の評価軸そのものに対するアンチテーゼなのです.