$$\def\mA{\mathbf{A}} \def\mB{\mathbf{B}} \def\mC{\mathbf{C}} \def\mD{\mathbf{D}} \def\mE{\mathbf{E}} \def\mF{\mathbf{F}} \def\mG{\mathbf{G}} \def\mH{\mathbf{H}} \def\mI{\mathbf{I}} \def\mJ{\mathbf{J}} \def\mK{\mathbf{K}} \def\mL{\mathbf{L}} \def\mM{\mathbf{M}} \def\mN{\mathbf{N}} \def\mO{\mathbf{O}} \def\mP{\mathbf{P}} \def\mQ{\mathbf{Q}} \def\mR{\mathbf{R}} \def\mS{\mathbf{S}} \def\mT{\mathbf{T}} \def\mU{\mathbf{U}} \def\mV{\mathbf{V}} \def\mW{\mathbf{W}} \def\mX{\mathbf{X}} \def\mY{\mathbf{Y}} \def\mZ{\mathbf{Z}} \def\va{\mathbf{a}} \def\vb{\mathbf{b}} \def\vc{\mathbf{c}} \def\vd{\mathbf{d}} \def\ve{\mathbf{e}} \def\vf{\mathbf{f}} \def\vg{\mathbf{g}} \def\vh{\mathbf{h}} \def\vi{\mathbf{i}} \def\vj{\mathbf{j}} \def\vk{\mathbf{k}} \def\vl{\mathbf{l}} \def\vm{\mathbf{m}} \def\vn{\mathbf{n}} \def\vo{\mathbf{o}} \def\vp{\mathbf{p}} \def\vq{\mathbf{q}} \def\vr{\mathbf{r}} \def\vs{\mathbf{s}} \def\vt{\mathbf{t}} \def\vu{\mathbf{u}} \def\vv{\mathbf{v}} \def\vw{\mathbf{w}} \def\vx{\mathbf{x}} \def\vy{\mathbf{y}} \def\vz{\mathbf{z}} \def\veps{\boldsymbol{\epsilon}} \def\vnu{\boldsymbol{\nu}} \def \vmu{\boldsymbol{\mu}} \def\mSigma{\boldsymbol{\Sigma}} $$
はじめに
普段は多チャネル音源分離などの研究に取り組んでいるものですが、SLAMやLidar odometry、自動運転に興味があり独学で勉強しています。自分の備忘録もかねて記事を書いていこうと思います。間違いなどがありましたら指摘して頂けると助かります。
内容はとりあえず以下を予定しています。
- Kalman filter (KF)
- Extended Kalman filter (EKF), Particle filter (PF)
- EKF-SLAM
- Graph-based SLAM
- Iterative Closest Point (ICP)
- Normal Distribution Transform (NDT)
- Generalized-ICP (GICP)
※ iPadで確認したところ何故か数式の前で改行してしまうようで現在対策を調査中です。もしかしたらiPhoneでも同じ問題が発生しているかもしれません。
参考文献
書籍
- Probabilistic robotics
- SLAM入門 (URL)
- Autowareではじめる自律移動技術入門 (URL)
- 詳解確率ロボティクス (URL)
- パターン認識と機械学習 上 (URL) 下 (URL)
※ hontoの提携書店(丸善など)で紙書籍を購入すると後で電子書籍を買うときに半額で買えるのでオススメです。
論文
- The Normal Distributions Transform: A New Approach to Laser Scan Matching, P. Biber et al., IEEE/RSJ IROS, 2003. (2D-NDT)
- The Three-Dimensional Normal-Distributions Transform --- an Efficient Representation for Registration, Surface Analysis, and Loop Detection, M. Magnusson, Doctoral Dissertation, 2009. (3D-NDT)
- Generalized ICP, V. Aleksandr et al., Robotics: Science and Systems, 2009. (GICP)
- A Tutorial on Graph-Based SLAM, G. Grisetti et al., IEEE Intelligent Transportation Systems Magazine, 2010. (Graph-based SLAM)
- Fast and accurate scan registration through minimization of the distance between compact 3D NDT representations, T. Stoyanov et al., Journal of Robotics Research, 2012. (D2D-NDT)
- Beyond Points: Evaluating Recent 3D Scan-Matching Algorithms, M. Magnusson et al., IEEE ICRA, 2015. (D2D-NDT)
- Voxelized GICP for Fast and Accurate 3D Point Cloud Registration, K. Koide et al., IEEE ICRA, 2021. (VGICP)
数式表記
- $x$(小文字+イタリック)$\rightarrow\ $スカラー
- $ \vx$(小文字+太字)$\rightarrow\ $列ベクトル
- $\mA$(大文字+太字)$\rightarrow\ $行列
- $\approx\ \rightarrow\ $近似
- $\vx \sim p(\vx) \rightarrow \ $確率変数$\vx$が分布$p(\vx)$に従う
Kalman filter
第1回目は一番基礎とも言えるKalman filter(KF)まわりの説明をしていこうと思います。KFは、ロボット位置などの推定したい隠れ状態とセンサなどから得られる観測との関係を状態空間モデルを用いてモデル化したときに適用可能な、隠れ状態を推論する手法の1つです。
状態空間モデル
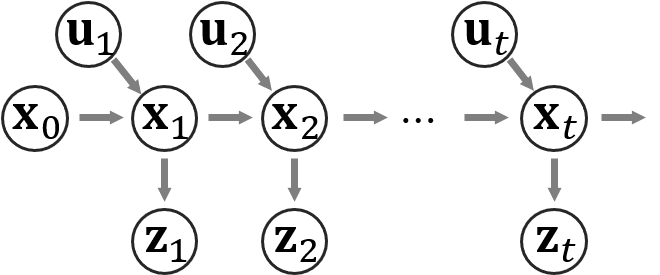
状態空間モデルというのは上の図のようなものを指します。この図で$\vx_t$は例えば時刻$t$でのロボットの位置などの状態を表し、$\vz_t$は時刻$t$でのセンサの観測値を表します。$\vu_t$は例えば$\vx_{t-1}$から$\vx_t$にロボットの状態が変化する際にコントローラなどから与えた指示や、オドメトリ(タイヤの回転数などから計算した移動量)などの情報を表します。この記事では、$\vx$を状態、$\vu$を操作、$\vz$を観測と呼ぶことにします。この状態空間モデルは変数間の関係を表しており、$\vx_{t-1}$と$\vx_t$の関係を状態遷移モデル、$\vx_t$と$\vz_t$の関係を観測モデルと呼びます。KFを適用して推論を行うためには、2つのモデルの設計の際に強い制約があり、以下の式で関係が表されないといけません。
\begin{align}
\vx_{t} &= \mA \vx_{t-1} + \vb + \veps \\
\vz_{t} &= \mC \vx_{t} + \vd + \vnu
\end{align}
ここで、$\veps \sim \mathcal{N}(\mathbf{0}, \mQ)$、$\vnu \sim \mathcal{N}(\mathbf{0}, \mR)$はガウス分布に従うノイズを表し、$\mQ$と$\mR$は自分で設定します。$\vb$は$\vu_t$から計算できる値とします。この$\mA, \vb, \mC, \vd$は$\vx$に依存しないものであり、とても強い制約になっていますが、これにより効率的な計算を行うことができます。複雑な変換を用いた状態空間モデルを設計した際に適用できる推論手法として後で紹介するExtended Kalman filter (EKF) やParticle filter (PF) などがあります。
この状態遷移モデルと観測モデルから以下の関係が成り立ちます。
\begin{align}
p(\vx_t | \vx_{t-1}, \vu_t) &= \mathcal{N}(\mA \vx_{t-1} + \vb, \mQ) \\
p(\vz_t | \vx_t) &= \mathcal{N}(\mC \vx_{t} + \vd , \mR)
\end{align}
Kalman filterの導出
KFで推定するのは$p(\vx_t | \vu_{1:t}, \vz_{1:t})$、つまり時刻1からtまでの観測と操作が与えられたときの時刻$t$での状態$\vx_t$の事後確率です。ただし、$\vz_{1:t}=[\vz_1, \ldots, \vz_t]$は時刻1からtまでの全ての観測を含んだものを表すこととします。初期状態$\vx_0$は、座標系が決まっていない場合には$\vx_0$を座標の原点とするために$\vx_0 = \mathbf{0}$とするか、座標系が決まっている場合にはおおよその位置を平均とするガウス分布に従うとしたりします(場所がわからないなら分散を大きく設定します)。
KFは$p(\vx_t | \vu_{1:t}, \vz_{1:t})$を逐次的に計算する手法で、$p(\vx_0) \rightarrow p(\vx_1 | \vu_1, \vz_1) \rightarrow p(\vx_2 | \vu_{1:2}, \vz_{1:2}) \rightarrow \cdots \rightarrow p(\vx_t | \vu_{1:t}, \vz_{1:t})$のように順番に計算していきます。各分布はガウス分布になることがわかっており、$p(\vx_{t-1} | \vu_{1:t-1}, \vz_{1:t-1}) = \mathcal{N}(\vx_{t-1} | \vmu_{t-1}, \mSigma_{t-1})$であるとして、$p(\vx_t | \vu_{1:t}, \vz_{1:t})$を計算していきます。
まずは以下のように$p(\vx_t | \vu_{1:t}, \vz_{1:t})$を書き直します。
\begin{align}
p(\vx_t | \vu_{1:t}, \vz_{1:t}) &= \frac{p(\vz_t | \vx_t, \vu_{1:t}, \vz_{1:t-1}) p(\vx_t | \vu_{1:t}, \vz_{1:t-1})}{p(\vz_t | \vu_{1:t}, \vz_{1:t-1})} \\
&\propto p(\vz_t | \vx_t, \vu_{1:t}, \vz_{1:t-1}) p(\vx_t | \vu_{1:t}, \vz_{1:t-1}) \\
&= p(\vz_t | \vx_t) p(\vx_t | \vu_{1:t}, \vz_{1:t-1}) \\
&= p(\vz_t | \vx_t) \int p(\vx_t, \vx_{t-1} | \vu_{1:t}, \vz_{1:t-1}) d\vx_{t-1} \\
&= p(\vz_t | \vx_t) \int p(\vx_t | \vx_{t-1}, \vu_t) p(\vx_{t-1} | \vu_{1:t-1}, \vz_{1:t-1}) d\vx_{t-1}
\end{align}
最初の式変換はベイズの定理によるもので、$\vu_{1:t}, \vz_{1:t-1}$を無視して考えるとわかりやすいと思います。KFの目的は先程述べたように$p(\vx_t | \vu_{1:t}, \vz_{1:t})$という$\vx_t$の事後分布を求めることなので、$p(\vz_t | \vu_{1:t}, \vz_{1:t-1})$は$\vx_t$に依存しない定数項とみなすことができ、2行目では比例記号$\propto$を使って、$p(\vz_t | \vu_{1:t}, \vz_{1:t-1})$を省略して書いています。3行目では状態空間モデルで表されているように、$\vz_t$が$\vx_t$にのみ依存しており、$\vx_t$が与えられているときは他の変数に依らないという仮定を用いています。4行目、5行目では$p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$を$\vx_{t-1}$についての周辺化を用いて書き直していて、最後にようやく$p(\vx_{t-1} | \vu_{1:t-1}, \vz_{1:t-1})$が現れています。
次に最後の行の積分部分を計算していきます。
\begin{align}
\int p(\vx_t | \vx_{t-1}, \vu_t) p(\vx_{t-1} | \vu_{1:t}, \vz_{1:t-1}) d\vx_{t-1} &= \int \mathcal{N}(\vx_t | \mA \vx_{t-1} + \vb, \mQ) \mathcal{N}(\vx_{t-1} | \vmu_{t-1}, \mSigma_{t-1}) d\vx_{t-1}\\
&= \cdots \\
&= \mathcal{N}(\vx_t | \mA \vmu_{t-1} + \vb, \mA \mSigma_{t-1} \mA^T + \mQ)
\end{align}
この途中計算について、Probabilistic roboticsなどの書籍では、ガウス分布を展開して$\vx_{t-1}$に関する項とそれ以外との項に分けて、ガウス分布のexp部分の積分が正規化項の値になるという性質などを用いて整理しており、なかなか複雑な計算を行っています。しかし、この部分は$\vx_t = \mA \vx_{t-1} + \vb + \epsilon$という関係式と、$p(\vx_{t-1} | \vu_{1:t}, \vz_{1:t-1}) = \mathcal{N}(\vx_{t-1} | \vmu, \mQ)$を用いて簡単に導出することができます。
\begin{align}
p(\mA \vx_{t-1} | \vu_{1:t}, \vz_{1:t-1}) &= \mathcal{N}(\vx_{t-1} | \mA \vmu_{t-1}, \mA \mSigma_{t-1} \mA^T) \\
p(\mA \vx_{t-1} + \vb | \vu_{1:t}, \vz_{1:t-1}) &= \mathcal{N}(\vx_{t-1} | \mA \vmu_{t-1} + \vb, \mA \mSigma_{t-1} \mA^T) \\
p(\mA \vx_{t-1} + \vb + \veps | \vu_{1:t}, \vz_{1:t-1}) &= \mathcal{N}(\vx_{t-1} | \mA \vmu_{t-1} + \vb, \mA \mSigma_{t-1} \mA^T + \mQ)
\end{align}
もし状態遷移モデルが$\vx_t = \mA \vx_{t-1}+\vb + \veps$のように表されなかったとすると上のような計算ができず、$p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$が計算できないという問題が発生します。
ここで、
\tilde{\boldsymbol{\mu}}_{t} = \mA \vmu_{t-1} + \vb \\
\tilde{\mSigma}_{t} = \mA \mSigma_{t-1} \mA^T + \mQ
と定義しておきます。最後に$p(\vz_t | \vx_t) p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$を計算していきます。
\begin{align}
p(\vz_t | \vx_t) p(\vx_t | \vu_{1:t}, \vz_{1:t-1}) = \mathcal{N}(\vz_t | \mC \vx_t + \vd, \mR) \mathcal{N}(\vx_{t} | \tilde{\vmu}_{t}, \tilde{\mSigma}_{t})
\end{align}
この式のexpの中身を$\vx_t$について整理すると、$\vx_t$の2次の項、$\vx_t$の1次の項、定数に分けることができ、これは$\vx_t$がガウス分布に従っているということを意味しています。このように整理できるのは、観測モデルが$\vz_t= \mC \vx_t + \vd + \vnu$のように制限されているためです。平均と分散共分散パラメータを求めるために、以下の式に着目します。
\begin{align}
\mathcal{N}(\vx | \vmu, \mSigma) &\propto \exp \left(-\frac{1}{2}(\vx - \vmu)^T \mSigma^{-1} (\vx - \vmu) \right) \\
&= \exp \left(-\frac{1}{2}\left( \vx^T \mSigma^{-1}\vx - 2\vx^T \mSigma^{-1}\vmu + \vmu^T \mSigma^{-1}\vmu \right) \right)
\end{align}
この式から分かるように$\vx$の2次の項が分散共分散行列の逆行列に対応し、$\vx$の1次の項が分散共分散行列の逆行列に平均を掛けたものに対応しているので、$p(\vz_t | \vx_t) p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$のexpの中身を整理した結果からまず分散共分散行列が計算できて、1次の項にそれを掛けることによって平均を計算することができます。計算過程は省略しますが、平均と分散は以下の式で与えられます。
\begin{align}
\mK_t &= \tilde{\mSigma}_t \mC^T (\mC \tilde{\mSigma}_t \mC^T + \mR)^{-1} \\
\vmu_t &= \tilde{\vmu}_t + \mK_t(\vz_t - (\mC \tilde{\vmu}_t + \vd)) \\
\mSigma_t &= (\mI - \mK_t \mC) \tilde{\mSigma}_t
\end{align}
ここで、$\mI$は単位行列を表し、$\mK_t$はカルマンゲインと呼ばれる行列を表します。
平均$\vmu_t$の計算式に着目してみると、$\mC \tilde{\vmu}_t + \vd$ は$\vx_t = \tilde{\vmu}_t$である場合の観測の推定値を表します。この観測の推定値と実際の観測値$\vz_t$を比較して、それがずれていた場合にはその値にカルマンゲインを掛けたものを使って今までの推定値$\tilde{\vmu}_t$を更新していくという仕組みになります。もし$\tilde{\vmu}_t$が正解に十分近ければ、$\vz_t - (\mC \tilde{\vmu}_t + \vd)$は0に近づくため、ほとんど状態は更新されないことになります。
以上がKalman filterの導出になります。
まとめ
Kalman filterを使う手順をまとめておきます。
- 自分が解きたい問題に応じて状態空間モデルを設計(状態遷移モデルと観測モデルを決める)
- $p(\vx_0)$の設定
- 新しい$\vu_t, \vz_t$が得られるたびに以下の式を用いて$p(\vx_t | \vu_{1:t}, \vz_{1:t})$のパラメータ $\vmu_t, \mSigma_t$を計算
\begin{align}
\tilde{\vmu}_{t} &= \mA \vmu_{t-1} + \vb \\
\tilde{\mSigma}_{t} &= \mA \mSigma_{t-1} \mA^T + \mQ \\
\mK_t &= \tilde{\mSigma}_t \mC^T (\mC \tilde{\mSigma}_t \mC^T + \mR)^{-1} \\
\vmu_t &= \tilde{\vmu}_t + \mK_t(\vz_t - (\mC \tilde{\vmu}_t + \vd)) \\
\mSigma_t &= (\mI - \mK_t \mC) \tilde{\mSigma}_t
\end{align}
KFでは状態空間モデルに対して強い制約があり、このままでは多くの問題に適用できないため、この問題を緩和したExtended Kalman filterとParticle filterについて次回は説明していきます。