# 初めに
全部で4本の記事に分けて書いています!
- 第1回 株価予測_可視化編
- 第2回 株価予測_LSTM ver.1
- 第3回 株価予測_LSTM ver.2
- 第4回 株価予測_アプリ化編
実装コード
前回の記事ではLSTMをkerasで実装して株価を予測しました!時系列データの予測にはRNNかLSTMが主流になってきていますからね。今回はPytorchを使って意思決定のためのデータ分析を前回と同様にLSTMで行いたいと思います。
このシリーズで行っている株価のチャート分析は意思決定のためのテクニカル指標に過ぎません。なので、予測に絶対は無いことと、株やFXで損する・得することの判断は自己責任でお願いします。ちなみに私は過去にFX(レバレッジ20倍)でテクニカル指標を過信し過ぎて。。。。なので皆さんも実際に取引する時はファンダメンタルズ分析もしっかり取り入れつつ、楽しく取引しましょう!!
今回の章立て
- 今回の趣旨
- 前処理
- 予測実装
- 結果
- 最後に
- 参考文献
今回の趣旨
以前私は、IWSMAI 2020で発表されたStock Market Prediction Using LSTM Recurrent Neural Networkを読みました。率直な感想としては、やはり現代でも株価予測に関するゴールデンスタンダードが無いから、株価を予測することは難しい。ということです。株価は不規則に動くのでシンプルなモデル(単回帰など)ではやはり予測が困難です。最近だとAIの株価予測などのサービスも出てきていますが、やはり確実に!とは言えないでしょう(そもそも論、予測に確実なんてない☜)。さて、私は前回(第2回 株価予測_LSTM ver.1)も使用していますが、今回もLSTMによる予測モデルを構築していきたいと思います。
何がしたいのか?
株価予測をするときにはさまざまなコンセプトがあると思います。以下では、なぜ今回**「LSTM ver.2」**を作成したのかについて
- 「第2回 株価予測_LSTM ver.1」
- 「論文:Stock Market Prediction Using LSTM Recurrent Neural Network」
と比較しながら示しています。
第2回 株価予測_LSTM ver.1
前回のモデルでは月曜日から木曜日までのデータを使用して金曜日の終値が上がるか下がるかの2クラス分類をLSTMで行いました。このとき、精度の評価指標としてはaccuracyを用いました。私みたいに短期的に利益を上げたい場合は明日の株価が気になるので2値分類は効果を発揮するでしょう。☜精度はいまいちでしたが。。。
論文:Stock Market Prediction Using LSTM Recurrent Neural Network
この論文では、LSTMを用いて株価を正確に予測するためにはどのくらい学習をすれば良いのか?について調べています。
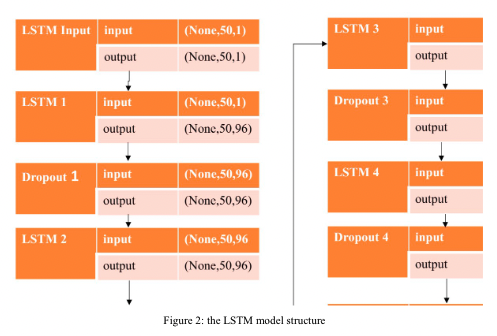
モデル構造はこんな感じで、LSTM4層で、途中にDropoutを挟んでいるという具合です。
データはNew York Stock ExchangeからGoogle(2004/8/19~2019/12/19)とNKE(2010/1/4~2019/12/19)のデータを取得して、学習データ80%、テストデー20%に分割して予測しています。
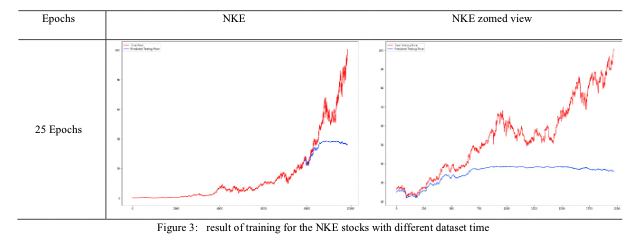
NKEのデータに関しては1980年からあるのですが、今回は使用していません(下図参照)。なぜなら、図からもわかるように1980年から2010年頃まで株価の変動率が低いためです。30年分の学習にオーバーフィッティングしていることによって、その後の大幅な株価の変動に予測が追いつけなくなっているわけです。
なので私も、どのようなデータを使用して株価予測をしようかと悩んだときに、過学習が起きないようなデータを収集することが重要だと考え、Zホールディングス(株)様からデータを取得しました。
前回の記事より図を参照
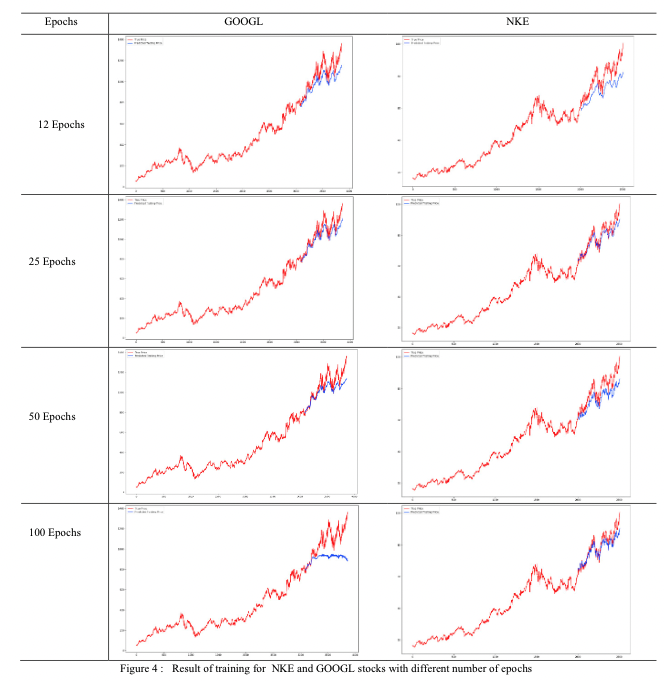
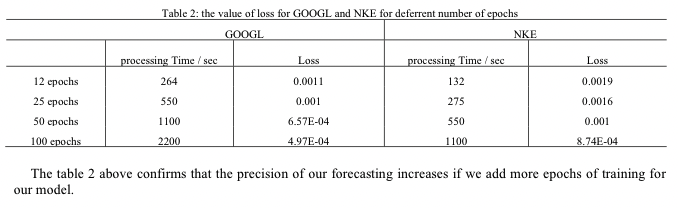
また、この論文ではEpochsが多くなるほどMSEが小さくなりました。という結論を出しています。
しかし、私としてはMSEではなく株価の値段も知りたいので、今回は前述を踏まえてLSTMのモデルを構築していきました。
今回の構築したLSTMモデルの特徴
使用するのはCloseデータのみです。今回は「データの期間:2005/01/01~2022/01/01」の25MAを利用して、「データの期間:2021/01/01~2022/01/01」の株価の予測を行いたいと思います。評価はMAEにしたので何円の誤差になるのかわかると思います。
前処理
今回もGoogle Colabで実装しています。
初めにライブラリのインポートをします。
# モジュールのインポート
import numpy as np
import pandas as pd
import pandas_datareader.data as data
from matplotlib import pyplot as plt
%matplotlib inline
# 標準化関数(StandardScaler)をインポート
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_absolute_error
import torch
from torch.utils.data import TensorDataset, DataLoader
from torch import nn
import torch.nn.functional as F
from torch import optim
前回と同様にデータを取得して、csvに保存していきます。
start = '2005-01-01'
end = '2022-01-01'
df = data.DataReader('4689.JP', 'stooq', start, end)
df.to_csv('Z_Holdings2.csv')
データの確認をします。
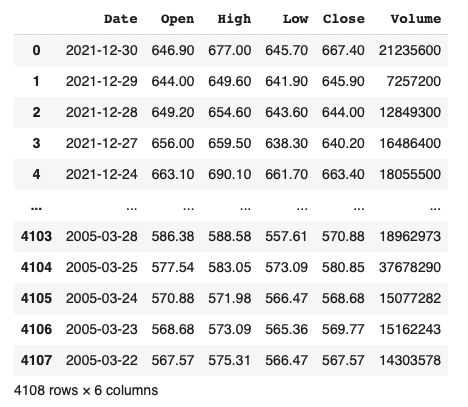
df = pd.read_csv('Z_Holdings2.csv')
df
カラムのデータ型の確認、欠損値の確認を行い、データを確認したら、Dateデータがobject型なので、datetime64型へ変更します。
df['Date'] = pd.to_datetime(df['Date'])
df.info()
始値(open)、安値(low)、高値(high)、出来高(volume)を消して、終値(close)のみを残します。
df = df.drop(['Open', 'Low', 'High', 'Volume'], axis=1)
次にデータの並び替えを行います。
df.sort_values(by='Date', ascending=True, inplace=True)
終値の25日移動平均(25MA)を算出してみます。
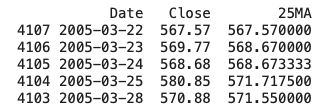
df['25MA'] = df['Close'].rolling(window=25, min_periods=0).mean()
print(df.head())
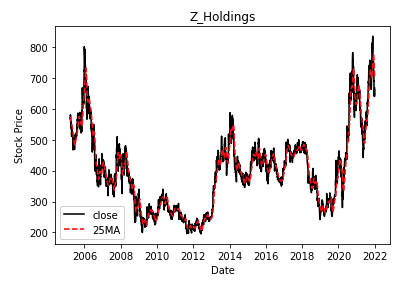
終値と25日移動平均を見てみましょう。
plt.figure()
plt.title('Z_Holdings')
plt.xlabel('Date')
plt.ylabel('Stock Price')
plt.plot(df['Date'], df['Close'], color='black',
linestyle='-', label='close')
plt.plot(df['Date'], df['25MA'], color='red',
linestyle='--', label='25MA')
plt.legend() # 凡例
plt.savefig('Z_Holdings.png') # 図の保存
plt.show()
問題ないようなので、入力する25MAを平均値が0、標準偏差が1になるように標準化を行います。
ma = df['25MA'].values.reshape(-1, 1)
scaler = StandardScaler()
ma_std = scaler.fit_transform(ma)
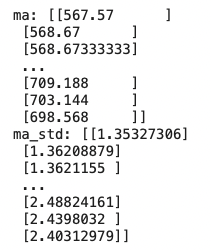
print("ma: {}".format(ma))
print("ma_std: {}".format(ma_std))
予測実装
いよいよ予測を行います。まず、現在から過去25日分の株価の移動平均を入力値として、1日後の株価の移動平均を予測するためのデータセットを作成します。このとき、効率的な処理をするためにN-dimensional arrayに変換します。
data = [] # 入力データ(過去25日分の移動平均)
label = [] # 出力データ(1日後の移動平均)
for i in range(len(ma_std) - 25):
data.append(ma_std[i:i + 25])
label.append(ma_std[i + 25])
# ndarrayに変換
data = np.array(data)
label = np.array(label)
print("data size: {}".format(data.shape))
print("label size: {}".format(label.shape))
今回の株価データを訓練データとテストデータに分けます。
test_len = int(252) # 1年分(252日分)
train_len = int(data.shape[0] - test_len)
# 訓練データ
train_data = data[:train_len]
train_label = label[:train_len]
# テストデータ
test_data = data[train_len:]
test_label = label[train_len:]
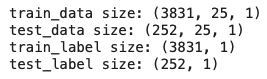
# データの形状を確認
print("train_data size: {}".format(train_data.shape))
print("test_data size: {}".format(test_data.shape))
print("train_label size: {}".format(train_label.shape))
print("test_label size: {}".format(test_label.shape))
次に、ndarrayをPyTorchのTensorに変換します。
train_x = torch.Tensor(train_data)
test_x = torch.Tensor(test_data)
train_y = torch.Tensor(train_label)
test_y = torch.Tensor(test_label)
最後にTensorDatasetで特徴量とラベルを結合したデータセットを作成します。
train_dataset = TensorDataset(train_x, train_y)
test_dataset = TensorDataset(test_x, test_y)
DataLoaderを使用して、データセットを128個のミニバッチに分割します。
train_batch = DataLoader(
dataset=train_dataset, # データセットの指定
batch_size=128, # バッチサイズの指定
shuffle=True, # シャッフルするかどうかの指定
num_workers=2) # コアの数
test_batch = DataLoader(
dataset=test_dataset,
batch_size=128,
shuffle=False,
num_workers=2)
# ミニバッチデータセットの確認
for data, label in train_batch:
print("batch data size: {}".format(data.size())) # バッチの入力データサイズ
print("batch label size: {}".format(label.size())) # バッチのラベルサイズ
break
次に、株価を予測するためのニューラルネットワークを定義していきます。
LSTMの実装に関して、一部はゼロから作るDeep Learning ❷ ―自然言語処理編を参照しています。
モデル構造
1層のLSTMと、1層の全結合層で構成しています。
class Net(nn.Module):
def __init__(self, D_in, H, D_out):
super(Net, self).__init__()
self.lstm = nn.LSTM(D_in, H, batch_first=True,
num_layers=1)
self.linear = nn.Linear(H, D_out)
def forward(self, x):
output, (hidden, cell) = self.lstm(x)
output = self.linear(output[:, -1, :])
return output
次にハイパーパラメータの定義をします。
D_in = 1 # 入力次元: 1
H = 200 # 隠れ層次元: 200
D_out = 1 # 出力次元: 1
epoch = 100 # 学習回数: 100
今回の実装でCPUとGPUどちらを使うかを指定します。
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
net = Net(D_in, H, D_out).to(device)
print("Device: {}".format(device))
Device: cpu
損失関数(平均二乗誤差: MSE)の定義と最適化関数(Adam)の定義を行います。
criterion = nn.MSELoss()
optimizer = optim.Adam(net.parameters())
学習・評価損失を保存するリストを作成します。そして学習を実行します。
train_loss_list = [] # 学習損失
test_loss_list = [] # 評価損失
# 学習(エポック)の実行
for i in range(epoch):
# エポックの進行状況を表示
print('---------------------------------------------')
print("Epoch: {}/{}".format(i+1, epoch))
# 損失の初期化
train_loss = 0 # 学習損失
test_loss = 0 # 評価損失
# ---------学習パート--------- #
# ニューラルネットワークを学習モードに設定
net.train()
# ミニバッチごとにデータをロードし学習
for data, label in train_batch:
# GPUにTensorを転送
data = data.to(device)
label = label.to(device)
# 勾配を初期化
optimizer.zero_grad()
# データを入力して予測値を計算(順伝播)
y_pred = net(data)
# 損失(誤差)を計算
loss = criterion(y_pred, label)
# 勾配の計算(逆伝搬)
loss.backward()
# パラメータ(重み)の更新
optimizer.step()
# ミニバッチごとの損失を蓄積
train_loss += loss.item()
# ミニバッチの平均の損失を計算
batch_train_loss = train_loss / len(train_batch)
# ---------学習パートはここまで--------- #
# ---------評価パート--------- #
# ニューラルネットワークを評価モードに設定
net.eval()
# 評価時の計算で自動微分機能をオフにする
with torch.no_grad():
for data, label in test_batch:
# GPUにTensorを転送
data = data.to(device)
label = label.to(device)
# データを入力して予測値を計算(順伝播)
y_pred = net(data)
# 損失(誤差)を計算
loss = criterion(y_pred, label)
# ミニバッチごとの損失を蓄積
test_loss += loss.item()
# ミニバッチの平均の損失を計算
batch_test_loss = test_loss / len(test_batch)
# ---------評価パートはここまで--------- #
# エポックごとに損失を表示
print("Train_Loss: {:.2E} Test_Loss: {:.2E}".format(
batch_train_loss, batch_test_loss))
# 損失をリスト化して保存
train_loss_list.append(batch_train_loss)
test_loss_list.append(batch_test_loss)
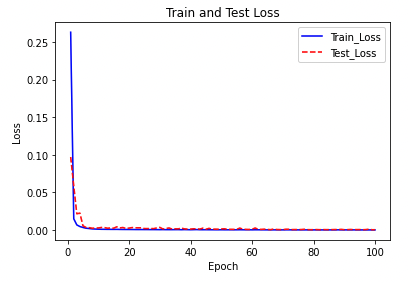
このとき、出力された値は標準化された株価の平均二乗誤差ですが、epochsを重ねるごとに損失は減少しています。学習データとテストデータに対するepochsごとの損失をプロットします。
# 損失
plt.figure()
plt.title('Train and Test Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.plot(range(1, epoch+1), train_loss_list, color='blue',
linestyle='-', label='Train_Loss')
plt.plot(range(1, epoch+1), test_loss_list, color='red',
linestyle='--', label='Test_Loss')
plt.legend() # 凡例
plt.show() # 表示
学習開始後すぐに損失の値が大幅に下がっていることがわかります。
学習していない最新の株価データ一年分を予測していきます。まず、ニューラルネットワークを評価モードに設定して株価の予測値と正解値を取得します。view(-1).tolist()で取得した予測値と正解値をTensorを1次元listに変換します。
net.eval()
# 推定時の計算で自動微分機能をオフにする
with torch.no_grad():
# 初期化
pred_ma = []
true_ma = []
for data, label in test_batch:
# GPUにTensorを転送
data = data.to(device)
label = label.to(device)
# 予測値を計算:順伝播
y_pred = net(data)
pred_ma.append(y_pred.view(-1).tolist())
true_ma.append(label.view(-1).tolist())
次に取得したlistが入れ子構造なので、Tensor数値データを取り出してlistを1次元配列にします。さらに今回は実際の株価の価格を知りたいので、標準化を解除して元の株価に変換します。
pred_ma = [elem for lst in pred_ma for elem in lst]
true_ma = [elem for lst in true_ma for elem in lst]
pred_ma = scaler.inverse_transform(pred_ma)
true_ma = scaler.inverse_transform(true_ma)
結果
平均絶対誤差を計算します。
mae = mean_absolute_error(true_ma, pred_ma)
print("MAE: {:.3f}".format(mae))
MAE: 2.043
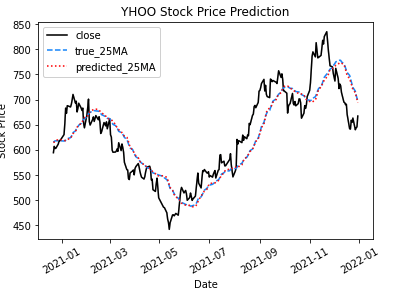
平均絶対誤差は約2ドルでした!これは、一年間の株価予測の予測値と正解値の結果の差が約2ドルということになります。最後に終値と25日移動平均を図示して結果を見てみましょう!
date = df['Date'][-1*test_len:] # テストデータの日付
test_close = df['Close'][-1*test_len:].values.reshape(-1) # テストデータの終値
plt.figure()
plt.title('YHOO Stock Price Prediction')
plt.xlabel('Date')
plt.ylabel('Stock Price')
plt.plot(date, test_close, color='black',
linestyle='-', label='close')
plt.plot(date, true_ma, color='dodgerblue',
linestyle='--', label='true_25MA')
plt.plot(date, pred_ma, color='red',
linestyle=':', label='predicted_25MA')
plt.legend() # 凡例
plt.xticks(rotation=30)
plt.show()
最後に
今回は過去数年分の株価データを用いることで、2021/1/1~2022/1/1までの株価を予測しました!結果としては一年間の株価予測の予測値と正解値の結果の差が約2ドルなので悪くはないと。。。個人的には思いますがどうでしょうか?今回作成したモデルのアーキテクチャや、前処理、データ取得時のデータの剪定で精度をより高めることができると思います。なのでこれからも時系列データ分析を勉強してもっと精度を高められるように頑張ります!(^○^)
参考文献
以下の書籍には大変お世話になりました、著者の皆様大変ありがとうございました!
最短コースでわかる ディープラーニングの数学
最短コースでわかる PyTorch &深層学習プログラミング
動かしながら学ぶ PyTorchプログラミング入門
FXデイトレード・スイングトレード
東大院生が考えたスマートフォンFX
ザ・トレーディング──心理分析・トレード戦略・リスク管理・記録管理
ガチ速FX 27分で256万を稼いだ“鬼デイトレ"
デイトレード
株とPython─自作プログラムでお金儲けを目指す本
Pythonで将来予測