Unityのクォータニオンの掛け算～順番によって結果が変わる理由と対策～

Last updated at 2024-11-16Posted at 2024-11-16

Unityのクォータニオンの掛け算～順番によって結果が変わる理由と対策～

Unityで3Dゲームを開発する際、オブジェクトの回転を扱うことがよくあります。

その中でも クォータニオン（Quaternion） は重要な役割を果たしますが、掛け算の順番によって計算結果が異なることをご存知でしょうか？

正しく理解していないと、バグの原因になることがあります！

本記事では、Unityにおけるクォータニオンの掛け算の順番による違いを説明し、どう扱えば良いのか解説します！

クォータニオンの基本

Unityで回転を扱いたい場合、オイラー角の方が直感的でわかりやすいですが、オイラー角にはジンバルロックを防げないという問題があります。

それを解決するのが クォータニオン です！

Unityでは、Quaternionクラスとして実装されています。

例えば、物体をX軸で-90°回転させたい場合、以下のように記述します。

transform.rotation = Quaternion.Euler(-90, 0, 0);

以下のようなイメージです。

無回転状態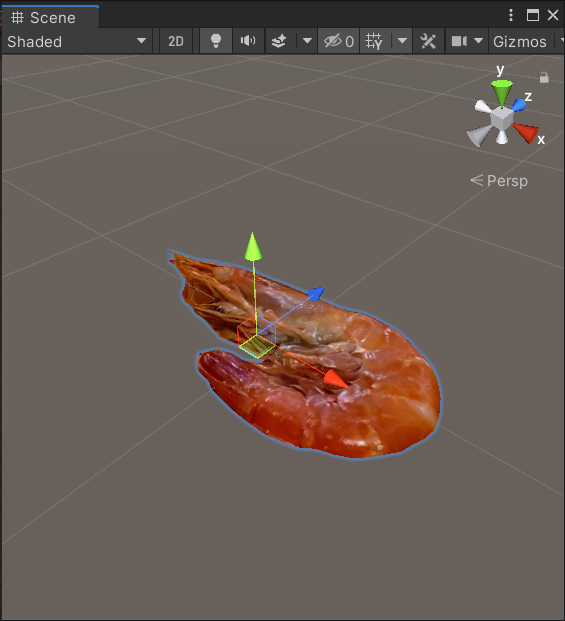
X軸で-90°回転

※ちなみに、この海老は自作モデルです。興味がある方はこちらへ

クォータニオンの掛け算

回転させた物体を更に回転させたい場合、 クォータニオンの掛け算 をします。

例えば、物体をX軸に-90°回転させた後で、Y軸で-90°回転させたい場合、以下のように記述します。

transform.rotation = Quaternion.Euler(0, -90, 0) * Quaternion.Euler(-90, 0, 0);

以下のように順番に回転していくイメージです。

無回転状態
X軸で-90°回転 `Quaternion.Euler(-90, 0, 0)`
X軸で-90°回転してからY軸で-90°回転 `Quaternion.Euler(0, -90, 0) * Quaternion.Euler(-90, 0, 0)`

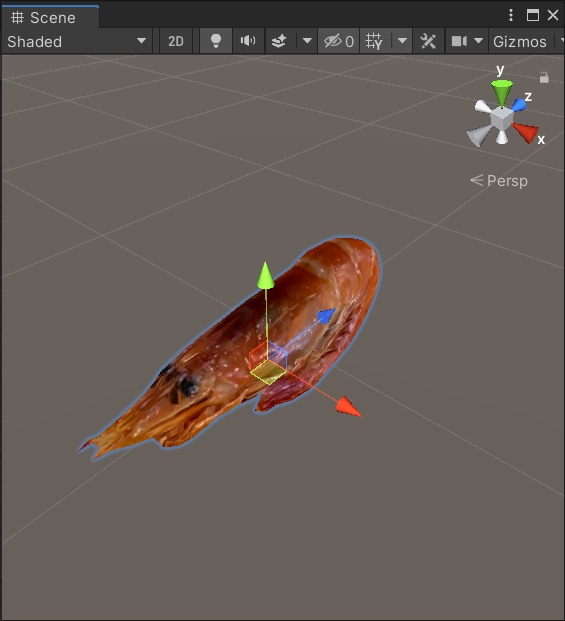クォータニオンの掛け算の順番

実はクォータニオンの掛け算には順番があります！

つまり、以下のプログラムは結果が異なります！

// Y軸回転 × X軸回転
transform.rotation = Quaternion.Euler(0, -90, 0) * Quaternion.Euler(-90, 0, 0);

// X軸回転 × Y軸回転
transform.rotation = Quaternion.Euler(-90, 0, 0) * Quaternion.Euler(0, -90, 0);

図で見比べると一目瞭然です。

無回転状態
X軸で-90°回転してからY軸で-90°回転 `Quaternion.Euler(0, -90, 0) * Quaternion.Euler(-90, 0, 0)`
Y軸で-90°回転してからX軸で-90°回転 `Quaternion.Euler(-90, 0, 0) * Quaternion.Euler(0, -90, 0)`

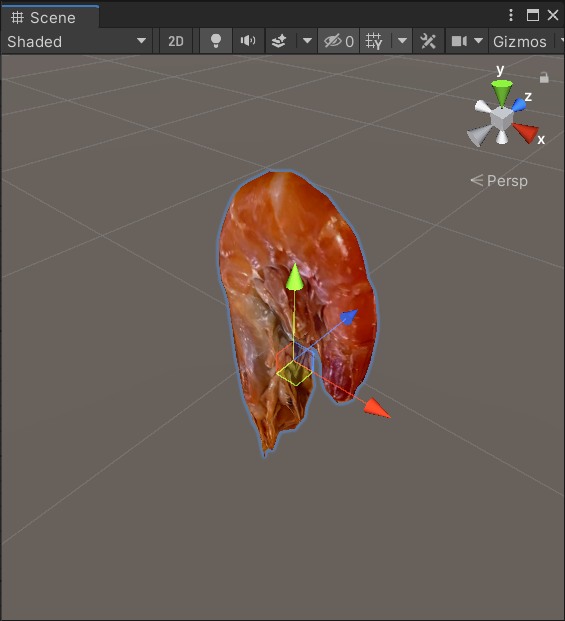ここで、掛け算の順番に注目します。

X軸回転した後にY軸回転したい場合は、Y軸回転 × X軸回転の順番で掛け算をしています
Y軸回転した後にX軸回転したい場合は、X軸回転 × Y軸回転の順番で掛け算をしています

そうなんです！順番が逆になるんです！！！
直感的に反する！！！

なので、クォータニオンの掛け算をするときは、 回転する順番の逆順に掛ける と覚えましょう！（なぜそうなるかは後述）

このことを意識してプログラミングをしないと、バグを生み出すことになります。

なぜ逆順なのか？

回転する順番の逆順に掛けると言われてもよくわからないですよね？

ここからはより詳しい解説をします。

今までは座標系が動かない前提で解説してきました。

しかし、クォータニオンが 座標系ごと回転している と考えると、直感的に理解しやすくなります。

クォータニオンの掛け算を次のように解釈してみます。

左側のクォータニオンが、座標系ごと物体を回転させ、新しい軸を定義する。
右側のクォータニオンが、新しく定義された軸にしたがって物体を回転をさせる。

つまり、Quaternion.Euler(0, -90, 0) * Quaternion.Euler(-90, 0, 0) は、以下のように解釈できます。

無回転状態
`Quaternion.Euler(0, -90, 0)` が、座標系ごと物体をY軸で-90°回転させ、新しい軸を定義する。 X軸（赤矢印）は直前でZ軸だった方向に向く。 Y軸（緑矢印）はY軸のまま。 Z軸（青矢印）は直前でX軸の反対だった方向に向く。
`Quaternion.Euler(-90, 0, 0)` が、座標系ごと物体をX軸で-90°回転させ、新しい軸を定義する。 X軸（赤矢印）はX軸のまま。 Y軸（緑矢印）は直前でZ軸の反対だった方向に向く。 Z軸（青矢印）は直前でY軸だった方向に向く。