言語処理100本ノック 2015の挑戦記録です。環境はUbuntu 16.04 LTS + Python 3.5.2 :: Anaconda 4.1.1 (64-bit)です。過去のノックの一覧はこちらからどうぞ。
第10章: ベクトル空間法 (II)
第10章では,前章に引き続き単語ベクトルの学習に取り組む.
99. t-SNEによる可視化
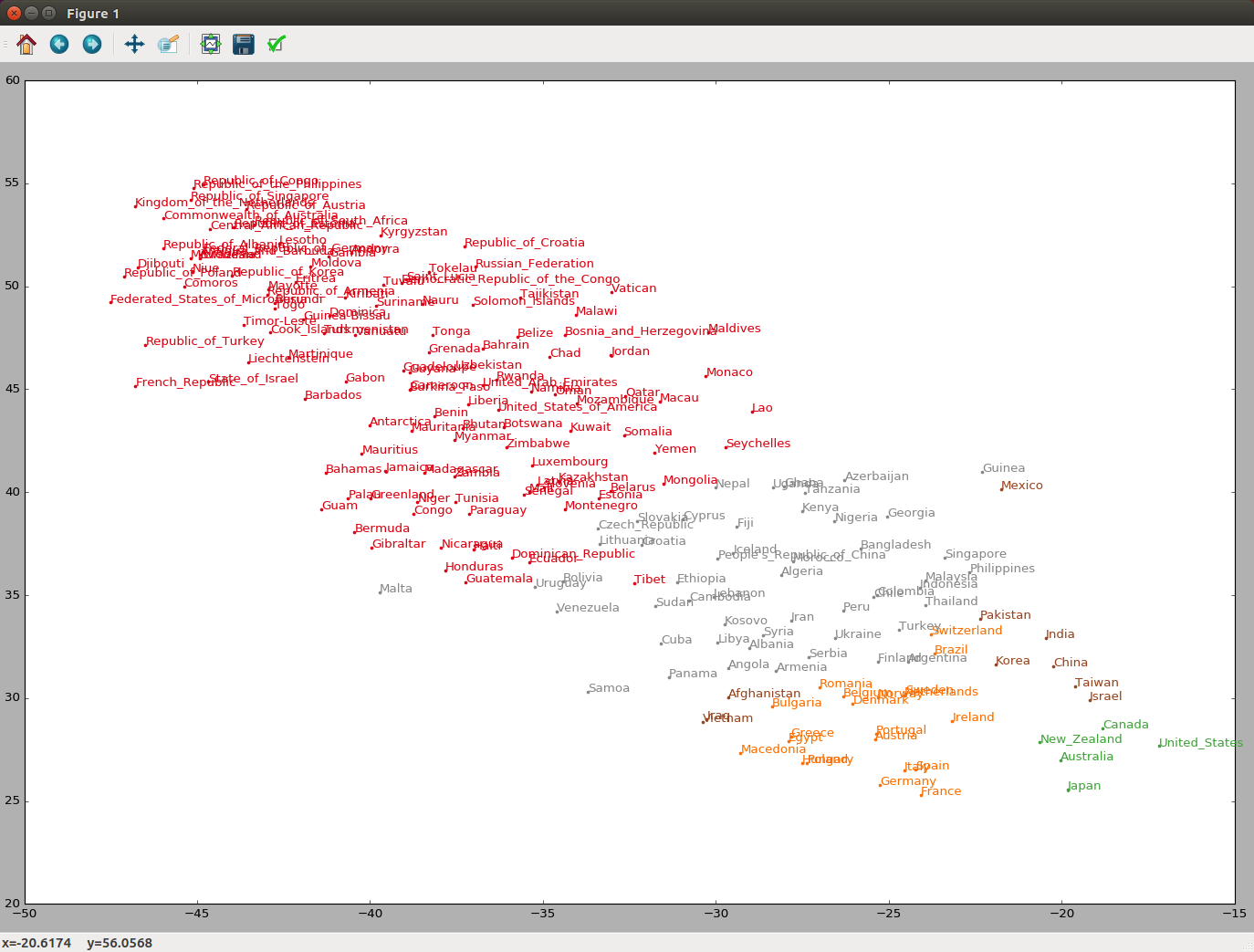
96の単語ベクトルに対して,ベクトル空間をt-SNEで可視化せよ.
出来上がったコード:
# coding: utf-8
import pickle
from collections import OrderedDict
from scipy import io
import numpy as np
from sklearn.manifold import TSNE
from matplotlib import pyplot as plt
from sklearn.cluster import KMeans
fname_dict_index_t = 'dict_index_country'
fname_matrix_x300 = 'matrix_x300_country'
# 辞書読み込み
with open(fname_dict_index_t, 'rb') as data_file:
dict_index_t = pickle.load(data_file)
# 行列読み込み
matrix_x300 = io.loadmat(fname_matrix_x300)['matrix_x300']
# t-SNE
t_sne = TSNE(perplexity=30, learning_rate=500).fit_transform(matrix_x300)
print(t_sne)
# KMeansクラスタリング
predicts = KMeans(n_clusters=5).fit_predict(matrix_x300)
# 表示
fig, ax = plt.subplots()
cmap = plt.get_cmap('Set1')
for index, label in enumerate(dict_index_t.keys()):
cval = cmap(predicts[index] / 4)
ax.scatter(t_sne[index, 0], t_sne[index, 1], marker='.', color=cval)
ax.annotate(label, xy=(t_sne[index, 0], t_sne[index, 1]), color=cval)
plt.show()
実行結果:
コンソールにはt-SNEの結果を表示します。終わりにGUI関連と思われるワーニングがいくつか表示されますが、とりあえず表示できているので見なかったことにしています^^;
[[-29.63311256 30.05717752]
[-29.02780193 32.43235393]
[-28.12066543 35.98851441]
[-40.55313784 51.62391537]
[-29.63700344 31.45330259]
[-40.02534455 43.24316715]
[-44.89162454 51.54464261]
[-24.44305919 31.77040681]
[-28.25881208 31.32557468]
[-20.03454468 27.00183735]
[-25.38516702 27.98530254]
[-26.28011683 40.58244161]
[-41.28383626 40.9369799 ]
[-36.75137704 46.95635693]
[-25.81774144 37.24545298]
[-41.89020189 44.53751707]
[-33.04680773 40.06303629]
[-26.31578973 30.09132208]
[-35.74178699 47.5599764 ]
[-38.14214307 43.70016633]
(中略)
[-38.3101884 50.69786382]
[-38.18742682 47.62544104]
[-37.52934351 39.50333772]
[-24.71963429 33.29939172]
[-41.33907508 47.73534094]
[-39.62433112 50.06006953]
[-28.35425406 40.24426661]
[-26.55941826 32.90395623]
[-36.73796908 45.17567413]
[-17.19551664 27.6777464 ]
[-36.30297687 44.01961458]
[-35.22625208 35.4037205 ]
[-37.54835761 45.98536944]
[-40.42385535 47.63098304]
[-33.01827771 49.73381647]
[-34.61202863 34.2208756 ]
[-30.38028055 28.84354115]
[-31.76946608 41.90241079]
[-37.56471174 40.7622317 ]
[-36.06250735 42.17539905]]
GLib-GIO-Message: Using the 'memory' GSettings backend. Your settings will not be saved or shared with other applications.
(python:7179): Gtk-WARNING **: GModule (/usr/lib/x86_64-linux-gnu/gtk-2.0/2.10.0/immodules/im-fcitx.so) initialization check failed: GLib version too old (micro mismatch)
(python:7179): Gtk-WARNING **: Loading IM context type 'fcitx' failed
(python:7179): Gtk-WARNING **: GModule (/usr/lib/x86_64-linux-gnu/gtk-2.0/2.10.0/immodules/im-fcitx.so) initialization check failed: GLib version too old (micro mismatch)
(python:7179): Gtk-WARNING **: Loading IM context type 'fcitx' failed
(python:7179): Gtk-WARNING **: GModule (/usr/lib/x86_64-linux-gnu/gtk-2.0/2.10.0/immodules/im-fcitx.so) initialization check failed: GLib version too old (micro mismatch)
(python:7179): Gtk-WARNING **: Loading IM context type 'fcitx' failed
t-SNEによる可視化
t-SNEは次元圧縮の手法の1つです。
問題85で主成分分析(PCA)を使った次元圧縮を学びましたが、主成分分析では失われる情報量が少なくなることを目的にしていました。それに対してt-SNEは、圧縮後でもデータ間の距離をなるべく維持するように次元圧縮を行います。そのため元データで距離が離れているものは、t-SNEで2次元や3次元に圧縮して可視化した場合も離れた位置に変換されるようになっています。
t-SNEの解説はググるとたくさん出てきますので、詳細は割愛します。ALBERTさんのホームページの解説t-SNE を用いた次元圧縮方法のご紹介が分かりやすかったです。
t-SNEの実装
t-SNEによる次元圧縮は、問題97のK-Meansでも使ったscikit-learnを使うと簡単です。sklearn.manifold.TSNEクラスで必要なパラメータを指定し、fit_transform()で行列を渡せば次元圧縮が実行されて、各行に対する新たな次元の行列が取得できます。デフォルトでは2次元に圧縮され、各行が2つの値の行列になります。
ただし、t-SNEのパラメータはデフォルトだと上手くいかないことがあり、perplexityとlearning_rateの調整が重要のようです。また、処理にランダムの要素があるそうで、実行の度に結果が変わります。そのため、random_stateを指定することで乱数のシード値を指定できるようになっています。
t-SNEのパラメータについては私もまだきちんとは理解できていないのですが、DeepAgeさんの高次元のデータを可視化するt-SNEの効果的な使い方が参考になりそうです。このページの最初の方には、収束の様子をアニメーションで確認できるシミュレーター?があり、見ているだけでもちょっと面白いです。
t-SNEの結果の可視化
散布図になるので実装方法問題39と同じですが、今回は点だけでなく国名のラベルも必要なため、pyplot.annotate()でラベルを指定しました。
これで可視化できたのはいいのですが、t-SNEのパラメータをいろいろ調節してみても、なかなかうまく塊ができません。そこで試しに問題97でやったK-Meansを再度実行して5分類し色をつけて見たところ、実行結果のように、なんとなく同じ色が集まっていることが確認できました。距離を意識した次元圧縮がうまくできているようです。
なお、色分けは定義済みのcolormapを使うと簡単です。matplotlib.cm.get_cmap()でcolormapが取得でき(ドキュメントには見つからなかったのですが、なぜかpyplot.get_cmap()でも取得できるのでコードではそうなっています)、それに対して0〜1の値を指定するとpyplot.scatter()などのcolorに指定できるRGBAのタプルが取得できます。定義済みのcolormapはこちらで確認できます。今回は「Set1」を使いました。
100本目のノックは以上です。誤りなどありましたら、ご指摘いただけますと幸いです。
実行結果には、100本ノックで用いるコーパス・データで配布されているデータの一部が含まれます。この第10章で用いているコーパス・データのライセンスはクリエイティブ・コモンズ 表示-継承 3.0 非移植(日本語訳)です。また、国名の一覧は、「KIDS外務省 - 世界の国々」(外務省)(http://www.mofa.go.jp/mofaj/kids/ichiran/index.html)と、nationsonline.orgのCountries and Regions of the World from A to Zを加工して作成しています。