最近はNLPを勉強しています。
記事の目的
統計学の論文を読んでいて出会した「全単射/bijective」という概念を上手く理解する、そして、次回定義を忘れた際に、(個人的に)秒で再理解できるような、ピンとくる喩えを思いついたので、メモします。
全単射の定義
Wikipediaからの引用
(左:全射でも単射でもない、右:単射であり全射でない)


(左:全射であり単射でない、右:全単射)
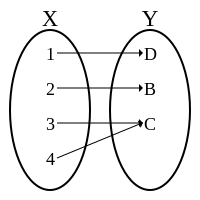

写像 f: A → B に対し、2つの条件
全射性: f(A) = B
単射性: 任意の A の元 a1, a2 について、f(a1) = f(a2) ならば a1 = a2
がともに成り立つとき、写像 f は全単射 (bijective) であるという。
$\forall b \in B, \exists ! a \in A s.t. b = f(a)$
全単射を喩えるとこんな感じ
全ての戸籍がデータベースに登録された日本を想定する。
始域Xを日本在住の父親の全体集合とし、その元を個々の父親、終域Yを日本在住の子供の全体集合とし、その元を個々の子供、fを特定の集合からそれぞれの子供を見つけ出す過程と喩えよう。
すると
全射性(surjective)とは、全ての日本在住の子供に対して、(少なくとも一人の)日本在住の父親がいる状態であり、
単射性(injective)とは、全ての日本在住の子供に対して、fで探し出せられるような日本在住の父親は一人しか存在しない状態である
と言える。
今回は日本在住という条件に絞ったので、全射性でないことに関しては、まあ海外にお父さんがいるのかなあと考えられるが、
単射性でないということになると、複雑な気持ちである。
この記事を作った背景
gloveの論文を読んでいますが、
準同型/homomorphismという概念を理解するのに詰まっており、
それを理解するために見ていたこちらの動画(英語)にて出てきた全単射/bijectiveという概念。
なんとか理解はできたのですが、しばらくするとド忘れしてしまうので、覚えやすいように分かりやすい喩えを考えてみましたという次第でした。