はじめに
入門書を何冊か読んでみたけど、そこからはみ出たことがなかなかできないといった方は多くいると思います。自分も独学でプログラミングの勉強をしておりそのような悩みを抱えていたため、このような記事を書いてみました。
現時点では、あまり初学者に有益な情報はないかもしれませんが、これから少しずつ追記していく予定です。
この記事は、「問題解決のPythonプログラミング
――数学パズルで鍛えるアルゴリズム的思考」の内容を基にして書いています。
この記事の内容
「[問題解決のpythonプログラミング]
(https://www.oreilly.co.jp/books/9784873118512/)」p146の練習問題の中に、3種類の方法で作成した要素数n個リストについて、それぞれのループ回数を計算せよ。といった内容のものがあったのですが、**せっかく計算したのでそれを可視化して、比較してみよう!**というのが本記事の内容となっています。
それでは実践!
クイックソートのアルゴリズムについて
def quickSort(lst, start, end):
'''
lst: ソートするリスト
start: pivotと比較していくリストの範囲の先頭の番号。初期値は必ず0
end: pivotと比較していくリストの範囲の最後の番号。lstの要素数 - 1
'''
global move
if start < end:
split, move = pivotPartition(lst, start, end)
quickSort(lst, start, split - 1)
quickSort(lst, split + 1, end)
return lst, move
def pivotPartition(lst, start, end):
global move
pivot = lst[end]
bottom = start - 1
top = end
done = False
while not done:
while not done:
move += 1
bottom += 1
if bottom == top:
done = True
break
if lst[bottom] > pivot:
lst[top] = lst[bottom]
#move += 1 if分の中で移動度をカウントすると、
#ソートの効率が正確に測れないので、コメントアウト
break
while not done:
move += 1
top -= 1
if top == bottom:
done = True
break
if lst[top] < pivot:
lst[bottom] = lst[top]
#move += 1 if分の中で移動度をカウントすると、
#ソートの効率が正確に測れないので、コメントアウト
break
lst[top] = pivot
return top, move
move = 0 #移動度をグローバル変数で定義
D = list(range(i, -1, -1)) #降順のリストを作成
sorted_list, move = quickSort(D, 0, len(D) - 1) #クイックソートを行う
このプログラムでは、内側のwhileループの回数を移動度moveとして定義しています。
この移動度moveを縦軸、リストの長さを横軸として、グラフを作成していくこととします。
「[問題解決のpythonプログラミング]
(https://www.oreilly.co.jp/books/9784873118512/)」p137~p145でクイックソートのアルゴリズムについて解説されているため、詳しい部分については省略させていただきます。
まずはシンプルに
最初に、降順のリストのみで、グラフを作成してみます。
コードはこんな感じです。
import numpy as np
import matplotlib.pyplot as plt
import numpy as np
Move = np.array([0])
Num = np.array([0])
for i in range(100):
move = 0 #移動度をグローバル変数で定義
D = list(range(i, -1, -1)) #降順のリストを作成
sorted_list, move = quickSort(D, 0, len(D) - 1)
Move = np.append(Move, move)
Num = np.append(Num, i)
fig, ax = plt.subplots()
ax.plot(Num, Move)
これの出力結果が以下の様になります。
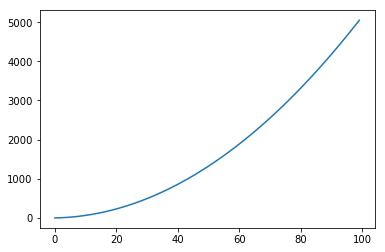
図1 降順リストをクイックソートでソートした場合の移動度
二種類の方法で作ったリストを比較
数値がランダムなリスト100個は以下のように作成した。
Move_R = np.array([0])
# ランダムなリストRを作成
for i in range(1, 101):
move = 0 # 移動度をグローバル変数で定義
R = [0] * i
R[0] = 29
for j in range(i):
R[j] = (9679 * R[i-1] + 12637 * j) % 2287
sorted_list, move = quickSort(R, 0, len(R) - 1)
Move_R = np.append(Move_R, move)
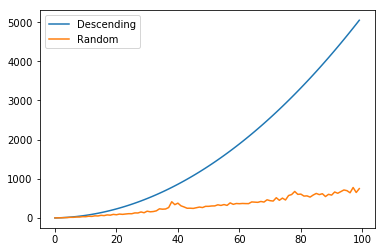
これまでに作成した乱数のリストRと降順リストLを比較していくことで、クイックソートの効率を分析していこうと思う。
ここで、比較を行うために、複数のグラフを同一の領域に描画する必要があるのだが、やり方はとても簡単で、単純に2度描画関数を呼ぶだけである。
そのためgurafu.pyの変更部分はこれだけ!
fig, ax = plt.subplots()
plt.plot(Num, Move, label = "Descending")
plt.plot(Num, Move_R, label = "Random")
plt.legend()
このグラフから、乱数のソートにおいて、クイックソートはとても安定したアルゴリズムであることが確認できたが、降順のリストにおいては、効率があまりよくないことが確認できた。