Ruby/Rust 連携 (5) Rutie で数値計算② ベジエ

連記事目次

• Ruby/Rust 連携 (1)　目的
• Ruby/Rust 連携 (2)　手段
• Ruby/Rust 連携 (3)　FFI で数値計算
• Ruby/Rust 連携 (4)　Rutie で数値計算①
• Ruby/Rust 連携 (5)　Rutie で数値計算②　ベジエ
• Ruby/Rust 連携 (6)　形態素の抽出
• Ruby/Rust 連携 (7)　インストール時ビルドの Rust 拡張 gem を作る

はじめに

前回は Ruby と Rust をつなぐ Rutie というものを使って，Rust の簡単な数値計算関数を Ruby から呼び出してみた。
速度面では，同じ計算を Ruby でやらせたのよりずっと遅かった。これは Ruby から Rust の関数を呼ぶコストがそこそこあったからだろう。そのコストに比して，やらせた数値計算が軽すぎた。

今回もまた Rutie を使い，Ruby から Rust を呼び出して数値計算をさせてみる。
前回と違うのは

• もう少しだけ複雑な計算をやらせる
• Rust で Ruby のクラスを作り，そのインスタンスのメソッドを呼び出す

というところ。
とくに，後者は重要で，これができれば Rust との連携でやれることがかなり広がる。

題材

ベジエ曲線の計算をさせてみたい。
参考：ベジェ曲線 - Wikipedia

3 次ベジエの場合，平面上に 4 つの点 $\boldsymbol{p}_0$, $\boldsymbol{p}_1$, $\boldsymbol{p}_2$, $\boldsymbol{p}_3$ を与えると曲線が決まる。
この曲線は以下のように媒介変数表示される。

\boldsymbol{p}(t) = (1-t)^3 \boldsymbol{p}_0 + 3t(1-t)^2 \boldsymbol{p}_1 + 3t^2(1-t) \boldsymbol{p}_2 + t^3 \boldsymbol{p}_3 \quad\quad (0 \leqq t \leqq 1)

すぐにわかるように，$t = 0$ のとき，$\boldsymbol p_0$ であり，$t=1$ のとき，$\boldsymbol p_3$ である。つまり，$\boldsymbol p_0$ から出発して $\boldsymbol p_3$ に至る曲線なわけだ。
$\boldsymbol{p}_1$ と $\boldsymbol{p}_2$ は一般には通らない（条件次第で通ることもある）。

$\boldsymbol p_1$ と $\boldsymbol p_2$ は制御点とも呼ばれ，$\boldsymbol p_1 - \boldsymbol p_0$ は $t=0$ における接ベクトルであるし，$\boldsymbol p_3 - \boldsymbol p_2$ は $t=1$ における接ベクトルである。

さて，やりたいことは，$\boldsymbol p_0$, $\boldsymbol p_1$, $\boldsymbol p_2$, $\boldsymbol p_3$ を与えたときに，任意の $t$ における位置 $\boldsymbol p(t)$ を得ることだ。

$x$ 座標と $y$ 座標は互いに関係しないので，$a_0$, $a_1$, $a_2$, $a_3$ に対して，

B(t) = (1-t)^3 a_0 + 3t(1-t)^2 a_1 + 3t^2(1-t) a_2 + t^3 a_3

という形の関数を考えればよい。
これを $x$ 座標用，$y$ 座標用それぞれ用意する。

この関数は 3 次のベルンシュテイン多項式と呼ばれている¹。つまり，今回のお題は「3 次のベルンシュテイン多項式の値を計算せよ」だ。

方針

さまざまな $t$ に対して，同じ係数（$a_0$, $a_1$, $a_2$, $a_3$）で計算をするわけだから，クラスを作ろう。
係数を与えてインスタンスを生成し，あとは $t$ を与えて多項式の値を計算させるのだ。

クラス名は，CubicBezier にしよう。いや，やっていることはベルンシュテイン多項式の計算なので CubicBernstein のほうが内容に合ってるかもしれないけど，「ベジエ」のほうが通りがいいしね。

Ruby で実装すると，

class CubicBezier
  def initialize(a0, a1, a2, a3)
    @a0, @a1, @a2, @a3 = a0, a1, a2, a3
  end
  
  def value_at(t)
    s = 1 - t
    @a0 * s * s * s + 3 * @a1 * t * s * s + 3 * @a2 * t * t * s + @a3 * t * t * t
  end

  alias [] value_at
end

てな感じ。

value_at に対して [] というエイリアスを当てているのは，やはり [] で計算させるほうが Ruby らしい感じがするのでは，と思ってのこと。

ともかく，これと同じ働きのクラスを Rutie で実装しようというわけ。

実装：Rust 側

インスタンス変数を持つようなクラスを Rutie でどうやって実装するのか。
幸い Rutie のコードには解説や例がついているので，それを見ながら試行錯誤してたら，なんか動くものができた。理屈は分かっていない。

Cargo.toml 編集まで

いままでと同様

cargo new cubic_bezier --lib

とやる。そして Cargo.toml　に

Cargo.toml

[dependencies]
lazy_static = "1.4.0"
rutie = "0.8.1"

[lib]
crate-type = ["cdylib"]

をぶっ込む。
今回は lazy_static クレートが必要になる。

（追記 2020-10-01）Rutie のバージョンを "0.7.0" としていたが，現時点の最新版 "0.8.1" に変更した。これにより，Rust 1.46 でコンパイルしたときに CubicBezier という名前について出ていた警告が出なくなる。なお，「0.7.0 だとコンパイルできたが 0.8.1 だとコンパイルできなかった」という方がいたら教えてください。

本体

方針

ぜんぜんよく分からないが，インスタンス変数を使うような Ruby のクラスを Rutie で定義する場合，Rust の構造体（struct）を用意し，それを wrap する，というやり方を取るものらしい（ここでいう wrap が何を意味するのかよく分からずに書いています）。
今の場合，a0，a1，a2，a3 というインスタンス変数を持つ CubicBezier という Ruby のクラスを作りたいので，そういうフィールドを持つ構造体をまず定義する。構造体の名前を CubicBezier とするとかぶってしまうので，仕方なく RustCubicBezier にする。
それを wrap するように CubicBezier を定義する。

コード

コードの全体はこのとおり。

src/lib.rs

#[macro_use]
extern crate lazy_static;

#[macro_use]
extern crate rutie;

use rutie::{Object, Class, Float};

pub struct RustCubicBezier {
    a0: f64,
    a1: f64,
    a2: f64,
    a3: f64,
}

impl RustCubicBezier {
    pub fn value_at(&self, t: f64) -> f64 {
        let s = 1.0 - t;
        self.a0 * s * s * s + 3.0 * self.a1 * t * s * s + 3.0 * self.a2 * t * t * s + self.a3 * t * t * t
    }
}

wrappable_struct!(RustCubicBezier, CubicBezierWrapper, CUBIC_BEZIER_WRAPPER);

class!(CubicBezier);

methods!(
    CubicBezier,
    rtself,

    fn cubic_bezier_new(a0: Float, a1: Float, a2: Float, a3: Float) -> CubicBezier {
        let a0 = a0.unwrap().to_f64();
        let a1 = a1.unwrap().to_f64();
        let a2 = a2.unwrap().to_f64();
        let a3 = a3.unwrap().to_f64();

        let rcb = RustCubicBezier{a0: a0, a1: a1, a2: a2, a3: a3};

        Class::from_existing("CubicBezier").wrap_data(rcb, &*CUBIC_BEZIER_WRAPPER)
    }

    fn value_at(t: Float) -> Float {
        let t = t.unwrap().to_f64();
        Float::new(rtself.get_data(&*CUBIC_BEZIER_WRAPPER).value_at(t))
    }
);

#[allow(non_snake_case)]
#[no_mangle]
pub extern "C" fn Init_cubic_bezier() {
    Class::new("CubicBezier", None).define(|klass| {
        klass.def_self("new", cubic_bezier_new);
        klass.def("value_at", value_at);
        klass.def("[]", value_at);
    });
}

以下の節で各部位に説明を加えていく。

RustCubicBezier

構造体とそのメソッドの定義：

pub struct RustCubicBezier {
    a0: f64,
    a1: f64,
    a2: f64,
    a3: f64,
}

impl RustCubicBezier {
    pub fn value_at(&self, t: f64) -> f64 {
        let s = 1.0 - t;
        self.a0 * s * s * s + 3.0 * self.a1 * t * s * s + 3.0 * self.a2 * t * t * s + self.a3 * t * t * t
    }
}

RustCubicBezier の定義は，あまり説明は要らないと思う。

Rust の関数は，第一引数を &self とかにして定義するとメソッドとして働く。

ラッパー

私にはよく意味の分からない箇所がこれ。

wrappable_struct!(RustCubicBezier, CubicBezierWrapper, CUBIC_BEZIER_WRAPPER);

さっき定義した構造体 RustCubicBezier と，ラッパーの関係を示しているらしい。

wrappable_struct! マクロのドキュメントはここ：
rutie::wrappable_struct - Rust（Rutie 0.7.0 版）

（追記 2020-10-01）現時点の Rutie 最新版は 0.8.1 だが，0.8 版はなぜか ドキュメント生成に失敗していて ページが存在しないので，ドキュメントへのリンクを 0.7.0 版のままにしている。

Rust の構造体を Ruby のオブジェクトで wrap できるようにする，とか何とか書いてあるような気がする（英語苦手）。

第一引数は wrap したい Rust の構造体の名前を与えるようだ。この構造体は public でなければならないそうなので，さきほど定義したときに pub を付けておいた。
第二引数は，第一引数を wrap するための構造体（ラッパー）の名前であるらしい。この構造体はマクロが自動的に定義してくれるとのこと。ただし，今回のコードでは第二引数として与えた CubicBezierWrapper が他の箇所には出てこない。
第三引数はラッパーを含む² static 変数の名前とのこと。

♪ 学ぶのやめたシニアエンジニア
♪ そんなお前は死にゃええんじゃ
♪ わくわく学ぶラストチャンス
♪ 反復スライス Rust の Chunk
♪ 叱ってくれよ鬼コンパイラ
♪ オレの頭はもう困憊だ

いや，ラッパーってそういうことじゃないから³。

クラスとメソッドの定義

まずクラス。これは単純。

class!(CubicBezier);

次にメソッド。

methods!(
    CubicBezier,
    rtself,

    fn cubic_bezier_new(a0: Float, a1: Float, a2: Float, a3: Float) -> CubicBezier {
        let a0 = a0.unwrap().to_f64();
        let a1 = a1.unwrap().to_f64();
        let a2 = a2.unwrap().to_f64();
        let a3 = a3.unwrap().to_f64();

        let rcb = RustCubicBezier{a0: a0, a1: a1, a2: a2, a3: a3};

        Class::from_existing("CubicBezier").wrap_data(rcb, &*CUBIC_BEZIER_WRAPPER)
    }

    fn value_at(t: Float) -> Float {
        let t = t.unwrap().to_f64();
        Float::new(rtself.get_data(&*CUBIC_BEZIER_WRAPPER).value_at(t))
    }
);

methods! マクロの定義はこちら：
https://docs.rs/rutie/0.7.0/src/rutie/dsl.rs.html#356-398

前回分からなかった，methods! マクロの第二引数の意味がおぼろげに分かりそうになった（後述）。

ここでは二つのメソッドを定義する。

cubic_bezier_new はインスタンスの生成（これが new になる）。

value_at は t に対してベルンシュテイン関数の値を計算するもの。

前回も書いたけど，この関数定義は，methods! マクロの引数であって，これがそのまま Rust の関数になるわけではない。マクロの働きで Rust の関数定義になるのだが，その際にゴニョゴニョやっている。
Rust のマクロをよく知っている人なら，上記リンク先を見ればだいたい理解できると思う。

cubic_bezier_new の中では，引数に基づいて，wrap すべき RustCubicBezier 型の構造体を生成している。
最終行の

Class::from_existing("CubicBezier").wrap_data(rcb, &*CUBIC_BEZIER_WRAPPER)

が肝なのだが，これまたよく分からない。
Class::from_existing("CubicBezier") は，要するに CubicBezier クラスを得ているらしい。Ruby でいうところの const_get("CubicBezier") みたいなもんか？

wrap_data のドキュメントはここ（いつか読む）：
rutie::Class - Rust

value_at のほうはだいぶ分かりやすい。
肝は

rtself.get_data(&*CUBIC_BEZIER_WRAPPER)

のところ。ここでようやく methods! マクロの第二引数 rtself が出てきた。
この式は，wrap した RustCubicBezier 構造体を返すようだ。
rtself はたぶん Ruby の self みたいな役割のものだろう。

初期化関数の定義

前回と同じ注意書きを。「初期化関数」というのは私が仮に名付けたもので，適切でないかもしれない。

#[allow(non_snake_case)]
#[no_mangle]
pub extern "C" fn Init_cubic_bezier() {
    Class::new("CubicBezier", None).define(|klass| {
        klass.def_self("new", cubic_bezier_new);
        klass.def("value_at", value_at);
        klass.def("[]", value_at);
    });
}

Init_cubic_bezier という名前の，外部から呼び出せる関数を定義している。
たぶん，これを実行することによって，実際に Ruby のクラスやメソッドが出来るのだと思う。

クラスメソッドには def_self を用い（これは前回と同じ），インスタンスメソッドには def を使うようだ。
Rust 側の value_at に対し，Ruby 側で value_at および [] を割り当てている。これで，CubicBezier#value_at と CubicBezier#[] がエイリアスのようになる。

ふー，まあ理解のおぼつかない箇所も少なくないけど，サンプルコードを参考にどうにかこうにか Rust 側のコードが出来た。
「原理が分かってないが何となく使えるものを組み合わせて動く」コードというのは 999スリーナイン の機関車みたい⁴。

コンパイル

プロジェクトのルートディレクトリーで

cargo build --release

とやると，target/release/libmy_rutie_math.dylib が出来る。ただし，拡張子は Linux だとたぶん .so だし，Windows だとたぶん .dll になる（.dylib なのは macOS の場合）。
Ruby 側で利用するのはこのファイルだけ。

実装：Ruby 側

Rust 側のコードがいくぶんややこしかったのに対し，Ruby 側のコードはいたってシンプル。

前回同様，以下のコードは，Rust のプロジェクトのルートディレクトリーに存在するとする。
（そうでない場合は，適宜 init メソッドの第二引数（あるいはそれと Rutie.new の lib_path）を適切に。

require "rutie"

Rutie.new(:cubic_bezier, lib_path: "target/release").init "Init_cubic_bezier", __dir__

cb = CubicBezier.new(1.0, 2.0, 1.5, 0.0)
0.0.step(1, by: 0.1) do |t|
  puts cb[t]
end

これで，3 次ベジエの計算が Ruby でできるようになった。
えっと，まともに使う場合は上のように横着せず，Gemfile に

Gemfile

gem "rutie", "~> 0.0.4"

とかって書いて Bundle.require してね。

おまけ：ベジエ曲線の絵を描かせる

せっかくベジエ曲線の計算ができるようになったので，絵を描かせておこう。
Cairo を使う。

require "rutie"
require "cairo"

Rutie.new(:cubic_bezier, lib_path: "target/release").init "Init_cubic_bezier", __dir__

size = 400

surface = Cairo::ImageSurface.new Cairo::FORMAT_RGB24, size, size
context = Cairo::Context.new surface

context.rectangle 0, 0, size, size
context.set_source_color :white
context.fill

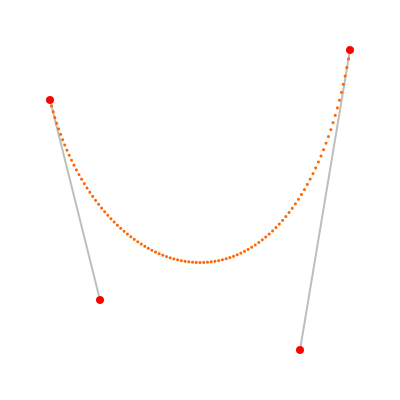
points = [[50, 100], [100, 300], [300, 350], [350, 50]]

bezier_x = CubicBezier.new(*points.map{ |x, _| x.to_f })
bezier_y = CubicBezier.new(*points.map{ |_, y| y.to_f })

context.set_source_color :gray
context.set_line_width 2
context.move_to(*points[0])
context.line_to(*points[1])
context.move_to(*points[2])
context.line_to(*points[3])
context.stroke

n = 100 # 分割数
context.set_source_color :orange
(1...n).each do |i|
  t = i.fdiv(n)
  context.circle bezier_x[t], bezier_y[t], 1.5
  context.fill
end

context.set_source_color :red
points.each do |x, y|
  context.circle x, y, 4
  context.fill
end

surface.write_to_png "bezier.png"

解説は略す（質問は歓迎）。
こんな絵が出来た。

赤い点は 3 次ベジエ曲線を規定する四つの点。灰色の線分は接ベクトル。オレンジの小さな点は，CubicBezier#[] で計算した，ベジエ曲線上の点だ。
このオレンジの点の並びを見て，「ああ，なんかちゃんと計算できてるぽい」と分かる。

ベンチマークテスト

さあ，いよいよベンチマークテストの時間ですよ。
そもそも今回の試みの目的の一つは，Rust によって高速化する実例を探ることだったんだからね。

今回も benchmark_driver を使うので，まだインストールしてない人は

gem i benchmark_driver

でインストールを。

テストコード

require "benchmark_driver"

Benchmark.driver do |r|
  r.prelude <<~PRELUDE
    require "rutie"
    Rutie.new(:cubic_bezier, lib_path: "target/release").init "Init_cubic_bezier", "#{__dir__}"

    class RubyCubicBezier
      def initialize(x0, x1, x2, x3)
        @x0, @x1, @x2, @x3 = x0, x1, x2, x3
      end

      def [](t)
        s = 1.0 - t
        @x0 * s * s * s + 3.0 * @x1 * t * s * s + 3.0 * @x2 * t * t * s + @x3 * t * t * t
      end
    end

    xs = [0.12, 0.48, 0.81, 0.95]
    rust_cubic_bezier = CubicBezier.new(*xs)
    ruby_cubic_bezier = RubyCubicBezier.new(*xs)
  PRELUDE

  r.report "rust_cubic_bezier[0.78]"
  r.report "ruby_cubic_bezier[0.78]"
end

これを走らせ，Ruby による実装と Rust による実装の比較をする。
あらかじめ言っておくと，Ruby から Rust を呼ぶためのコストがあるので，Rust 版のほうが遅い，という可能性は十分にある。

さて，結果はというと：

rust_cubic_bezier[0.78]:   6731741.2 i/s
ruby_cubic_bezier[0.78]:   4733084.6 i/s - 1.42x  slower

か，勝った，Rust 版が勝ったぞ！　ひゃほーい！！

まあ，1.4 倍速程度なので，大したことない，と言えば，ない。はっきり言って。
しかし，この程度の（わりと単純な）関数でも Rust で高速化できることを示せた意義はあると思う。
また，それが数十行程度の Rust コードで実現できる，という点にも希望が持てた。

今後はもっといろいろな処理を Rust でやらせてみて実用性を探っていきたい。

1. この多項式の名前は英語風の「バーンスタイン多項式」とかドイツ語風の「ベルンシュタイン多項式」と書かれることもあるが，旧ソビエト連邦の数学者 Бернштейн にちなむので，ロシア語風に「ベルンシュテイン多項式」とした。Wikipedia の セルゲイ・ベルンシュテイン によれば，出身地は黒海に面した都市オデッサ。現在はウクライナ共和国だが，当時はロシア帝国であったらしい。なお，この姓はイディッシュ語（ユダヤドイツ語）で琥こ珀はくの意である。 ↩

2. 原文で「contain」となっていたので「含む」としたが，単に「値として持つ」（〜が代入されている）という意味だろうか？ ↩

3. 音楽に疎くヒップホップとか全く知らないんで，ラップの歌詞がこういうものなのかどうか分からんけどテキトーに作詞してみた。 ↩

4. 松本零士作『銀河鉄道999』に出てくる銀河超特急 999 号の機関車は，宇宙の遺跡から発見された未知の文明による技術（中身はいまひとつ分からないが，どうにか使えるもの）を組み合わせて作られている。確かそういう設定だったはず。 ↩