はじめに
定常状態のシュレディンガー方程式は,差分法により行列の(一般)固有値問題に帰着させることが可能である。
本稿ではその方法を用いて3次元等方調和振動子ポテンシャル中の電子の固有エネルギーおよび固有関数を決定することを目的とする。
行列法のあらましについては
[Pythonによる科学・技術計算]行列形式による常微分方程式の境界値問題の解法,数値計算[1]
を参考にしていただければ幸いです。
内容
3次元等方調和振動子ポテンシャル
$V(r) = \frac{m_e \omega^2r^2}{2} {\tag {1}}$
に対する動径方向の波動関数$R(r)$に対する定常状態のシュレディンガー方程式は,
$u(r) = r R(r) {\tag{2}}$
として,
$-u''(r)+\frac{2 m_e}{\hbar^2}(V(r)+\frac{L(L+1)\hbar^2}{2m_e r^2}) = E \ u(r) {\tag {3}}$
であたえられる。
この方程式は合流型超幾何微分方程式へと変換でき,原点で正則な解のエネルギー固有値$E$の厳密解は
$E_n = \frac{\hbar \omega}{2} (n+\frac{3}{2}),\ ( \ n = 4N+2L+3 {\tag{4}})$
**であることが知られている[2]。**ここでLは軌道量子数, Nは自然数 $N=0,1,2,...$である。
したがってエネルギースペクトルは
$E = \hbar \omega [1.5, 2.5, 3.5, ...] {\tag{5}})$
となる。そのほんとんどが縮退している。
本稿では方程式(3)を行列の固有値問題として解きエネルギー固有値$E_n$および固有関数$u_n(r)$を計算する。
コード
コードはすべてRydberg原子単位を用いる。
これは,
電子の質量$m=1/2$
ディラック定数$\hbar =1$
長さをボーア$a_{B}=(0.529177 Å)$単位,
エネルギーを$1Ry=13.6058 eV
とするものである。
"""
行列法による境界値問題
3次元等方調和振動子ポテンシャル
"""
import numpy as np
import scipy.linalg
import matplotlib.pyplot as plt
delta_x = 0.05
x0, x1 = 0.001, 10
N=int((x1-x0)/delta_x)
print("N=",N)
L=0 # 軌道量子数。適宜変更する。
hbar=1
m_elec=1/2
omega=1
y = np.zeros([N-1,N+1])
y[:,0] = 0
y[:,-1] = 0
A=np.zeros([N-1,N-1])
B=np.identity(N-1)
v = np.zeros([N-1])
vcent = np.zeros([N-1])
veff = np.zeros([N-1])
for i in range(N-1): #調和振動子ポンシャル
x = x0 + i*delta_x
vcent[i] = L*(L+1)/x**2 # 遠心力ポテンシャル
v[i] = m_elec*omega**2*(x**2)/2
veff[i] = v[i] +vcent[i]
for i in range(N-1): # 3重対角行列なのでindexの位置を気をつけること
if i == 0:
A[i,i] = 2/(delta_x**2) + veff[i]
A[i,i+1] = -1/(delta_x**2)
elif i == N-2:
A[i,i-1] = -1/(delta_x**2)
A[i,i] = 2/(delta_x**2) + veff[i]
else:
A[i,i-1] = -1/(delta_x**2)
A[i,i] = 2/(delta_x**2) + veff[i]
A[i,i+1] = -1/(delta_x**2)
eigen, vec= scipy.linalg.eigh(A,B)
print("eigen values_3points=",eigen[0:4])
for j in range(N-1):
for i in range(1,N):
y[j, i] = vec[i-1,j]
#
# for plot
X= np.linspace(x0,x1, N+1)
plt.plot(X, y[0,:],'-',markersize=5,label='y1')
plt.plot(X, y[1,:],'-',markersize=5,label='y2')
plt.plot(X, y[2,:],'-',markersize=5,label='y3')
plt.legend(loc='upper right')
plt.xlabel('X') # x軸のラベル
plt.ylabel('Y') # y軸のラベル
plt.show()
結果
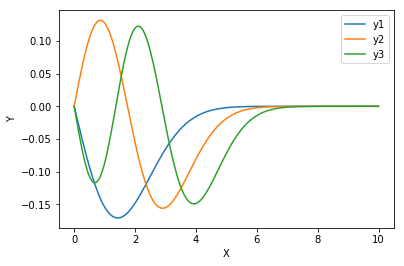
L=0
eigen values_3points= [ 1.46118173 3.44087896 5.42483146]
厳密値 1.5, 3.5, 5.5とは数%の誤差内で一致している。
$u_n(r)$ n=0, 2, 4の関数形を下図に示す。
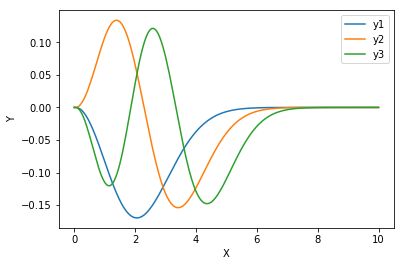
L=1
eigen values_3points= [ 2.4997526 4.49899205 6.49760609]
厳密値 2.5, 4.5, 6.5とは数%の誤差内で一致している。
補遺
ポテンシャルの関数形が変わる場合,単にv[i]の計算式を変えるだけでよい。
参考文献
[1] [Pythonによる科学・技術計算]行列形式による常微分方程式の境界値問題の解法,数値計算
[2]後藤 憲一 ほか, 『詳解理論応用量子力学演習』, 共立出版, 1982.