$[0,1]$の一様乱数$x$から与えられた確率密度関数$g(t)$を持つ非一様乱数を求める。
**モンテカルロ法を用いた計算統計力学では特定の分布を持つ乱数を発生させることがしばしば必要となる。**本稿はそのための基礎となる。
一般論:非一様乱数を生成するための関数
概略を述べる。ここでは数学的厳密性は追求せず直感的な理解を得られることを目的としている。読者諸氏にはその点についてご寛容いただき,また,内容に不備があればご指摘いただきたい...。
さて,
区間[0,1]の一様乱数の確率密度関数
$f(x)=1 \ (0\le x \le1), \ 0$ (その他) $\tag{1}$
から,任意の確率密度関数$g(t(x))$を持つ非一様乱数を与えるための$t$と$x$の関係,
$t=w(x) \tag{2}$
を求めたい。
まず,"確率の保存"の要請から,
$f(x)dx = g(t)dt \tag{3}$
である。式(1)を用いると
$dx = g(t)dt \Leftrightarrow x(t) = \int_{−∞}^{t} g(t')dt'+C \tag{3'}$
を得る。ここで, $C$は積分定数である。十分条件として$x(-∞) = C=0$ととる。このとき$\int_{−∞}^{∞} g(t')dt'=1$であるから, $x(∞) = 1$となる。
以上から, xとtの関係は
$x(t)=\int_{−∞}^{t} g(t')dt'\tag{4}$
によって結ばれていることがわかる。$g(t)$は与えるものである。ここからtをxの関係として求め式(2)の$w(x)$を決定すれば(逆関数を求めれば),そのtは非一様分布g(t)を与える確率変数となる。以上が任意の確率分布$g(t)$に従う乱数を発生させる手続きである。
内容
(1) 指数関数的な分布,
$g(t)$=
$ exp(-t)$ (t>0),
0 (t< 0))
に従う非一様乱数を求める。
(2) 平均値が$t_{av}$, 標準偏差が$\sigma$のガウス分布にしたがう非一様乱数を求める。通常の方法では逆関数を求めることが難しいため,2次元平面での関数密度を極座標に変換するボックス-ミュラー法を用いる。
(1): 指数分布
式(4)を用いる。
$x(t)=\int_{−∞}^{t} g(t')dt'=\int_{0}^{t} exp(-t') dt' = 1- exp(-t)$
であるから,ここからtをxの関数として求めると
$t=w(x)=- ln(1-x) \tag{5}$
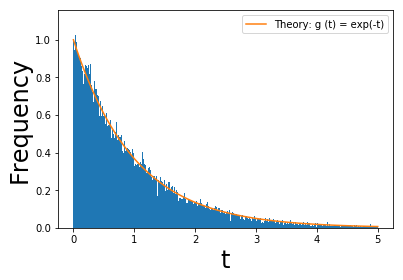
を得る。[0,1]の一様乱数をxに与えると,式(5)によってtの分布が決まり,それらは指数関数g(t)=exp(-t)として分布するのである。
それを以下のプログラムで確かめよう。
"""
x=[0,1]の一様乱数から指数関数型の非一様分布に従う乱数の発生
"""
from random import random
import numpy as np
from math import log
import matplotlib.pyplot as plt
data_lis=[]
N=10**6 # [0,1]の一様乱数のデータ点数 (N->∞で頻度分布が確率密度関数となる)
for n in range(N):
x=random()
t=-log(1-x) # x->t への変換: t = -log(1-x)
data_lis.append(t)
# plot
fig=plt.figure()
ax=fig.add_subplot(111)
Nbins=int(N/100)
ax.hist(data_lis, range=(0,5),bins=Nbins,normed=True) # [0,5]の範囲でNbins等分した規格化された棒グラフの作成
# 理論確率密度分布 y = exp(-x)
xx=np.linspace(0,5,100)
yy=np.exp(-xx)
plt.plot(xx,yy, label='Theory: g (t) = exp(-t)')
plt.legend(loc='best')
plt.xlabel('t',size=24)
plt.ylabel('Frequency', size=24)
plt.show()
結果(1)
x=[0,1]で100万点サンプルしたものから式(5)を用いてtを生成しそれの頻度分布を描いたもの。理論曲線$g(t)=exp(-t)$を再現していることが分かる。
(2) ガウス分布
平均値$t_{av}$, 標準偏差$\sigma$のガウス分布,$g(t)=(2 \pi \sigma^2)^{-1/2} \ exp(\frac{-(t-t_{av})^2}{2 \sigma^2})$
をボックス-ミュラー法により生成する。
2つの一様乱数変数xとyから,この場合は2つの独立なガウス分布を持つ非一様乱数に従う変数$t_1$と$t_2$が得られる。
$t_1 = \sigma \ [(-2ln(x))^{1/2} \ cos(2 \pi y)+t_{av} ]$
$t_2 = \sigma \ [(-2ln(x))^{1/2} \ sin(2 \pi y)+t_{av} ]$
これを確かめてみよう。
以下のコードは$\sigma=1$,$t_{av}=10$としてモンテカルロシミュレーションを行ったものである。
"""
ガウス分布を生成する非一様乱数
ボックス-ミュラーの方法
"""
from random import random
from math import cos, sin, pi, log, sqrt
import numpy as np
import matplotlib.pyplot as plt
data_lis1=[]
# data_lis2=[]
N=10**5 # [0,1]の一様乱数のデータ点数 (N->∞で頻度分布が確率密度関数となる)
sigma=1.0 #標準偏差
ave=10 # 平均値
for n in range(N):
x1=random()
x2=random()
t1=sigma*((-2*log(x1))**(1/2))*(cos(2*pi*x2))+ave #x->t への変換:
t2=sigma*((-2*log(x1))**(1/2))*(sin(2*pi*x2))+ave #x->t への変換:
data_lis1.append(t1)
# data_lis2.append(t2)
# plot
fig=plt.figure()
ax=fig.add_subplot(111)
Nbins=int(N/100)
# ax.hist(data_lis, range=(0,10),bins=Nbins,normed=True) # [0,5]の範囲でNbins等分した規格化された棒グラフの作成
"""
[0,∞]のガウス分布にして正規化してしまうと,本来の積聞値が0.5なのに1にするため数値が頻度が二倍に勘定されてしまうことに注意! 平均値を大きめにすると良い.
"""
ax.hist(data_lis1, range=(0,20),bins=Nbins,normed=True) # [0,5]の範囲でNbins等分した規格化された棒グラフの作成
# ax.hist(data_lis2, range=(0,20),bins=Nbins,normed=True) # [0,5]の範囲でNbins等分した規格化された棒グラフの作成
# 理論確率密度分布
xx=np.linspace(0,20,100)
yy=(1/sqrt(2*pi*sigma**2))*np.exp((-(xx-ave)**2)/(2*sigma**2)) # ガウス分布
plt.plot(xx,yy, label='Theory')
plt.legend(loc='best')
plt.xlabel('t',size=24)
plt.ylabel('Frequency', size=24)
plt.show()
結果(2)
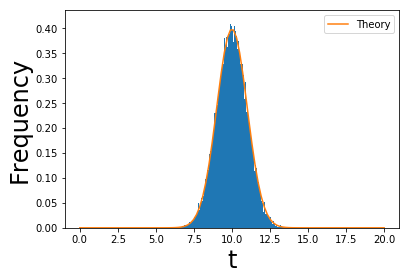
オレンジの線が理論曲線(ガウス関数)である。頻度分布がガウス分布を再現していることがわかる。
補遺
逆関数が見つからないことがしばしば起きる。その場合は数値的な評価や,他の方法を考える必要がある。メトロポリス法は計算物理学でよく使われる。
追記:2017年8月11日
メトロポリス法を用いたモンテカルロシミュレーションの記事を投稿しました。
[Pythonによる科学・技術計算] 与えられた確率密度関数を与える非一様乱数の生成,モンテカルロシミュレーション