はじめに
常微分方程式の解法の一つである4次のルンゲ-クッタ法によるニュートン方程式の数値解法の例を挙げる。
内容
(1) [ウォーミングアップ] 4次のルンゲ-クッタ法による1階常微分方程式の解法。
(2) 調和振動子
(3) 減衰振動
(4) 強制振動
内容(1): 1階常微分方程式の解法
import numpy as np
import matplotlib.pyplot as plt
"""
4次のルンゲ-クッタ法による1階常微分方程式
The fourth-order Runge-Kutta method for the 1st order ordinary differencial equation
dx/dt = -x^3+sin(t)を解く
"""
def f(x,t):
return -x**3 +np.sin(t)
a = 0.0
b = 10.0
N = 100
h = (b-a)/N
tpoints = np.arange(a,b,h)
xpoints = []
x = 0.0
for t in tpoints:
xpoints.append(x)
k1 = h*f(x,t)
k2 = h*f(x+0.5*k1, t+0.5*h)
k3 = h*f (x+0.5*k2, t+0.5*h)
k4 = h*f(x+k3, t+h)
x += (k1+2*k2+2*k3+k4)/6
plt.plot (tpoints, xpoints)
plt.xlabel("t")
plt.ylabel("x(t)")
plt.show()
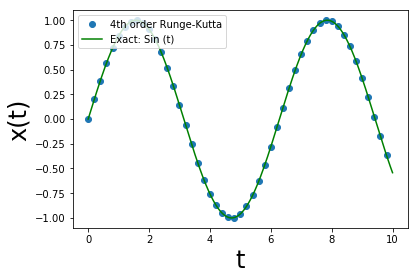
内容(2):調和振動子
import numpy as np
import matplotlib.pyplot as plt
"""
4次のルンゲ-クッタ法による1次元ニュートン方程式の解法
The fourth-order Runge-Kutta method for the 1D Newton's equation
# 例: 線形復元力 (harmonic oscilation)
"""
def f(x, v, t):
return -k*x # 復元力
M = 1.0 # mass: 1 Kg
k = 1.0 #ばね定数
t0 = 0.0
t1 = 10.0
N = 50
del_t = (t1-t0)/N # time grid
tpoints = np.arange(t0, t1, del_t)
xpoints = []
vpoints = []
# initial condition
x0 = 0.0
v0 = 1.0
x, v = x0, v0
for t in tpoints:
xpoints.append(x)
vpoints.append(v)
k1v =f(x, v, t)*del_t /M
k1x = v * del_t
k2v = f(x+k1x/2, v+k1v/2, t+del_t/2 )*del_t /M
k2x =(v+k1v/2)*del_t
k3v =f (x+k2x/2, v+k2v/2, t+del_t/2 )*del_t /M
k3x =(v+k2v/2 ) *del_t
k4v = f(x+k3x, v+k3v, t+del_t )*del_t /M
k4x = (v+k3v )*del_t
v += (k1v + 2 * k2v + 2* k3v + k4v)/6
x += (k1x + 2 * k2x + 2* k3x + k4x)/6
plt.plot (tpoints, xpoints, 'o',label='4th order Runge-Kutta')
plt.xlabel("t", fontsize=24)
plt.ylabel("x(t)", fontsize=24)
tt=np.arange(t0, t1, 0.01*del_t)
plt.plot (tt, np.sin(tt), '-',label='Exact: Sin (t)',color = 'Green')
plt.legend(loc='upper left')
plt.show()
plt.plot (tpoints,vpoints, 'o',label='4th order Runge-Kutta')
plt.xlabel("t", fontsize=24)
plt.ylabel("v(t)", fontsize=24)
tt=np.arange(t0, t1, 0.01*del_t)
plt.plot (tt, np.cos(tt), '-',label='Exact: Cos (t)', color = 'red')
plt.legend(loc='upper left')
plt.show()
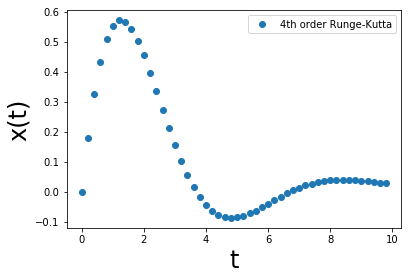
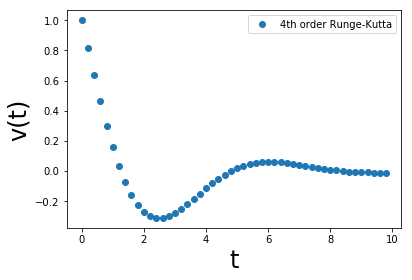
内容(3)減衰振動
import numpy as np
import matplotlib.pyplot as plt
"""
減衰振動
Damped oscillation
"""
def f(x, v, t):
k=1.0
a=1.0
return -k*x-a*v
M = 1.0 # mass: 1 Kg
t0 = 0.0
t1 = 10.0
N = 50
del_t = (t1-t0)/N # time grid
tpoints = np.arange(t0, t1, del_t)
xpoints = []
vpoints = []
# initial condition
x0 = 0.0
v0 = 1.0
x, v = x0, v0
for t in tpoints:
xpoints.append(x)
vpoints.append(v)
k1v =f(x, v, t)*del_t /M
k1x = v * del_t
k2v = f(x+k1/2, v+k1v/2, t+del_t/2 )*del_t /M
k2x =(v+k1v/2)*del_t
k3v =f (x+k2x/2, v+k2v/2, t+del_t/2 )*del_t /M
k3x =(v+k2v/2 ) *del_t
k4v = f(x+k3, v+k3v, t+del_t )*del_t /M
k4x = (v+k3v )*del_t
v += (k1v + 2 * k2v + 2* k3v + k4v)/6
x += (k1x + 2 * k2x + 2* k3x + k4x)/6
plt.plot (tpoints, xpoints, 'o',label='4th order Runge-Kutta')
plt.xlabel("t", fontsize=24)
plt.ylabel("x(t)", fontsize=24)
# tt=np.arange(t0, t1, 0.01*del_t)
# plt.plot (tt, np.sin(tt), '-',label='Exact: Sin (t)',color = 'Green')
plt.legend(loc='upper right')
plt.show()
plt.plot (tpoints,vpoints, 'o',label='4th order Runge-Kutta')
plt.xlabel("t", fontsize=24)
plt.ylabel("v(t)", fontsize=24)
# tt=np.arange(t0, t1, 0.01*del_t)
# plt.plot (tt, np.cos(tt), '-',label='Exact: Cos (t)', color = 'red')
plt.legend(loc='upper right')
plt.show()
内容(4)強制振動
import numpy as np
import matplotlib.pyplot as plt
"""
強制振動
Forced vibration
"""
def f(x, v, t):
k=1.0
gamma=0.1
return -k*x-2* gamma *v + 2*sin(t)
M = 1.0 # mass: 1 Kg
t0 = 0.0
t1 = 50.0
N = 1000
del_t = (t1-t0)/N # time grid
tpoints = np.arange(t0, t1, del_t)
xpoints = []
vpoints = []
# initial condition
x0 = 0.0
v0 = 1.0
x, v = x0, v0
for t in tpoints:
xpoints.append(x)
vpoints.append(v)
k1v =f(x, v, t)*del_t /M
k1x = v * del_t
k2v = f(x+k1/2, v+k1v/2, t+del_t/2 )*del_t /M
k2x =(v+k1v/2)*del_t
k3v =f (x+k2x/2, v+k2v/2, t+del_t/2 )*del_t /M
k3x =(v+k2v/2 ) *del_t
k4v = f(x+k3, v+k3v, t+del_t )*del_t /M
k4x = (v+k3v )*del_t
v += (k1v + 2 * k2v + 2* k3v + k4v)/6
x += (k1x + 2 * k2x + 2* k3x + k4x)/6
plt.plot (tpoints, xpoints, 'o',label='4th order Runge-Kutta')
plt.xlabel("t", fontsize=24)
plt.ylabel("x(t)", fontsize=24)
# tt=np.arange(t0, t1, 0.01*del_t)
# plt.plot (tt, np.sin(tt), '-',label='Exact: Sin (t)',color = 'Green')
plt.legend(loc='upper right')
plt.show()
plt.plot (tpoints,vpoints, 'o',label='4th order Runge-Kutta')
plt.xlabel("t", fontsize=24)
plt.ylabel("v(t)", fontsize=24)
# tt=np.arange(t0, t1, 0.01*del_t)
# plt.plot (tt, np.cos(tt), '-',label='Exact: Cos (t)', color = 'red')
plt.legend(loc='upper right')
plt.show()
補遺
ここで行ったルンゲ-クッタ法では,系の保存量の一つである全エネルギーは時間ステップの増加に伴い数値的には保存されなくなる。これを改善する(シンプレクティック性を持たせる)解法の一つがベルレー法である(Qiita記事を参照)。