[Pythonによる科学・技術計算] クランク-ニコルソン法(陰解法)とFTCS法(陽解法)による1次元非定常熱伝導方程式の数値解法，放物型偏微分方程式

#はじめに
物質中の温度勾配により原子の振動(格子振動)エネルギーが輸送される。これが熱伝導である[1]。その結果，物質の温度が時間経過に伴い変化し，最終的には時間変化しなくなる。定常状態に到達したのである。熱伝導は日常にありふれた現象であり，それの工学的応用(伝熱工学)は今日の生活を支える基盤の一つとなっている。

温度変動を記述する非定常熱伝導方程式は放物型偏微分方程式に分類される。
初等的な数値解法として，空間に中心差分法，時間発展に対して前進差分を用いる陽解法(FTCS)がある[2]。FTCS法は分かりやすく実装も容易であるが，微分方程式の数値安定性は高くない。

クランク-ニコルソン法[2]は数値安定性に優れた(無条件安定)陰解法の一つである。時間発展を計算するために連立一次方程式を解く必要があり，FTCS法に比べて実装が面倒ではあるが，安定性に加えて時間発展に対する誤差も小さく放物型偏微分方程式を解くための有用な手法の1つである。

ここではクランク-ニコルソン法によって1次元非定常熱伝導方程式を解く。

#内容
内部発熱$q(x,t)$, 一定の熱拡散率$D$を持つ物体の温度$T(x,t)$の従う熱方程式，

$ \frac{\partial T(x,t)}{\partial t} = D \frac{\partial^2 T(x,t)}{\partial x^2} +q(x,t)$

$D = \frac{\kappa} {\rho\  C_V}$

$T(x,0)=20$ (初期条件)
$T(0,t) = 0$ (境界条件)
$T(100,t) = 50$ (境界条件)

を

(1)クランク-ニコルソン法で解く。
ここで$\kappa$は熱伝導率，$\rho$は密度，$C_v$は等積比熱である。

(2) FTCS法で解く。

#計算コード

##(1)クランク-ニコルソン法
忠実な実装。1次元連立方程式を解くためにnumpyのlinalg.solveメソッドを使っている。

"""
1次元非定常熱伝導
クランク-ニコルソン法
"""

%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np


Nx =100 # x方向のグリッド点数
Nt =5000# t 方向のグリッド点数
Lx =0.01
Lt =1.5
delta_x=Lx/Nx
delta_t=Lt/Nt
r=delta_t/(delta_x**2)
print("r=",r)

uu = np.zeros([Nx,Nt])  # 求める関数


# 初期条件
#for i in range(1,Nx-1):
uu[:,0] = 20   # 初期条件

#  境界条件
for i in range(Nt):
    uu[0,i] = 0  
    uu[-1,i] = 50

p=np.ones([Nx,Nt])
for i in range(Nx):
    p[i,:] =4e-6

#print("stability=",p[0,0]*r)
q=np.zeros([Nx,Nt])

alpha=np.ones([Nx,Nt])
for i in range(Nx):
    alpha[i,:]= r*p[i,:]/2

# メイン
for j in range(Nt-1):

    Amat=np.zeros([Nx-2,Nx-2])  #連立一次方程式の係数行列の生成
    for i in range(Nx-2):
        Amat[i,i] = 1/alpha[i,j] +2
        if i >=1 :
            Amat[i-1,i] = -1
        if i <= Nx-4 :
                Amat[i+1,i] = -1

    
    bvec=np.zeros([Nx-2]) # Ax=bのbベクトルの生成
    for i in range(Nx-2):
        bvec[i] =  uu[i,j]+ (1/alpha[i+1,j] - 2)*uu[i+1,j]+uu[i+2,j]+q[i+1,j]
    bvec[0] += uu[0,j+1]
    bvec[Nx-3] += uu[-1,j+1]
    
    uvec = np.linalg.solve(Amat ,bvec) #連立一次方程式を解く
    for i in range(Nx-2):
        uu[i+1,j+1]=uvec[i]
        
#for 可視化
x=list(range(Nx))
y=list(range(Nt))

X, Y = np.meshgrid(x,y)

def functz(u):
    z=u[X,Y]
    return z

Z = functz(uu)
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_wireframe(X,Y,Z, color='r')
ax.set_xlabel('t')
ax.set_ylabel('x')
ax.set_zlabel('T')

plt.show()

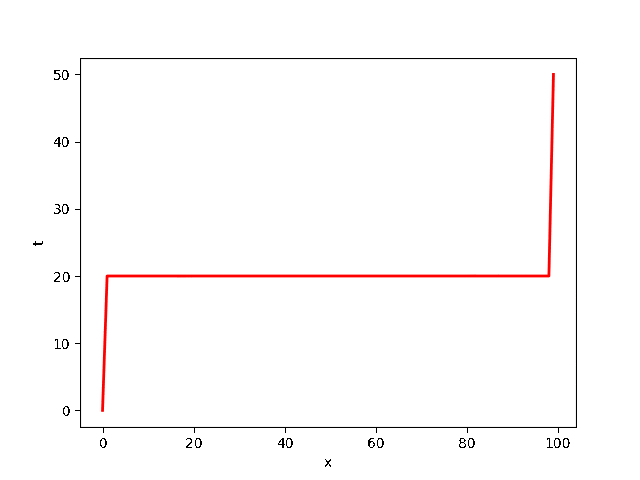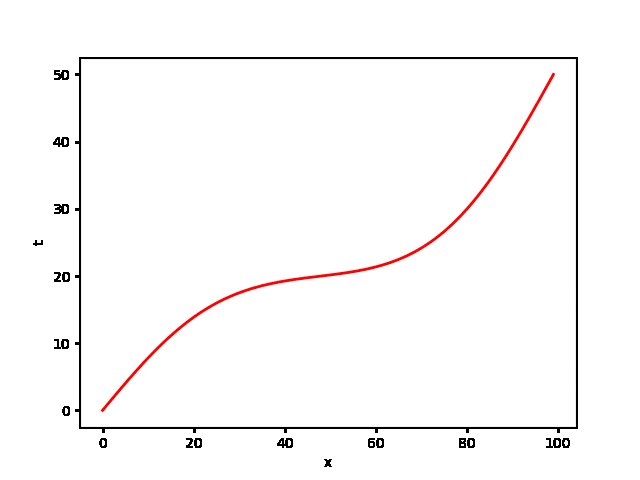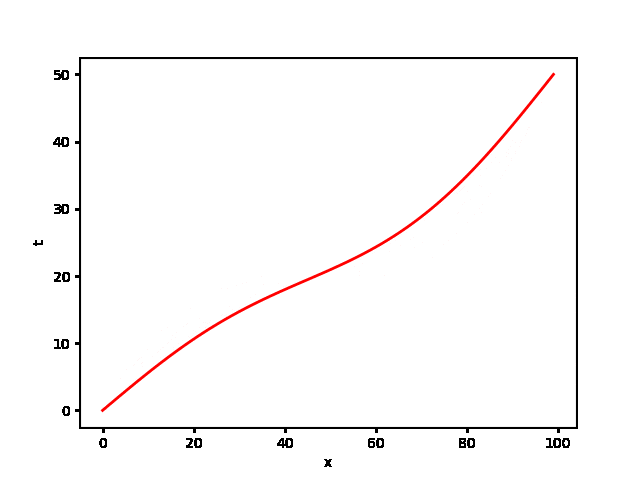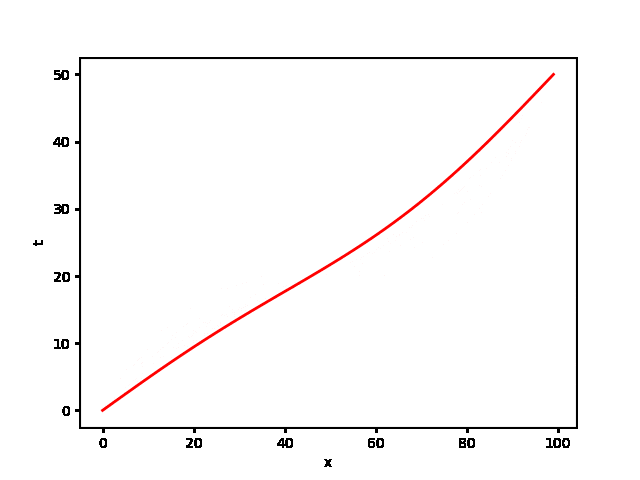
解のプロット。

---

次に，熱平衡状態に至るまでの様子をアニメーションで見てみる。

%matplotlib nbagg 
from matplotlib.animation import ArtistAnimation # アニメーション作成のためのメソッドをインポート

fig = plt.figure()

anim = [] #アニメーション用に描くパラパラ図のデータを格納するためのリスト
for i in range(Nt):
    T=list(uu[:,i])
    x=list(range(Nx))
    if i % int(Nt*0.02) ==0: 
        im=plt.plot(x,T, '-', color='red',markersize=10, linewidth = 2, aa=True)
        anim.append(im)

anim = ArtistAnimation(fig, anim) # アニメーション作成    
plt.xlabel('x')
plt.ylabel('t')

fig.show() 

anim.save("t.gif", writer='imagemagick')   #アニメーションをt.gifという名前で保存し，gifアニメーションファイルを作成する。

時間が経つにつれて温度が一定(定常状態)に近づく。

#(2) FTCS法

"""
1次元非定常熱伝導
FTCS法
"""

#%matplotlib nbagg
#matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation # アニメーション作成のためのメソッドをインポート

# 定数
L = 0.01
D= 4e-6 # 熱拡散率
N=100 # 刻み数
del_L= L/N # 空間刻み幅
del_t=  0.0001#時間刻み幅
dum = del_t/1000

print("stability=",D*del_t/(del_L**2))

T_low = 0.0
T_mid = 20.0
T_high=50.0

# 図示する
t1 = 0.01
t2 = 0.1
t3 = 0.4
t4 = 1.0
t5 = 10.0 
t_end = t5 +dum 

#
T = np.empty(N+1)
T[0] = T_high
T[N] = T_low
T[1:N] = T_mid

Tp = np.empty(N+1)
Tp[0] = T_high
Tp[N] = T_low

# メイン

t = 0.0
c =  del_t*D/(del_L**2)

while t < t_end :
    # 温度の計算
   # for i in range(1,N):
    #   Tp[i] = T[i] + c*(T[i+1]+T[i-1]-2*T[i])
    Tp[1:N] = T[1:N] + c*(T[0:N-1]+T[2:N+1]-2*T[1:N])

    T, Tp = Tp, T
    t += del_t
    
    #セレクトしたtでplot
    
    if np.abs(t-t1) < dum :
        plt.plot(T, label='t = t1')
        
    if np.abs(t-t2) < dum :
        plt.plot(T, label='t = t2')
    if np.abs(t-t3) < dum :
        plt.plot(T, label='t = t3')    
    if np.abs(t-t4) < dum: 
        plt.plot(T, label='t = t4')
    if np.abs(t-t5) < dum :
        plt.plot(T, label='t = t5')

plt.xlabel('x', fontsize=24)
plt.ylabel('T', fontsize=24)
plt.legend(loc='best')


plt.show()

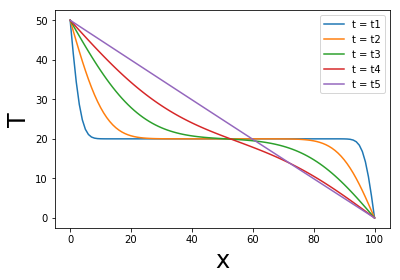
いくつかの時間をセレクトして温度プロファイルをプロットしたもの。

---

#参考文献
[1] 熱伝導方程式の導出については，
Qiita記事: 「熱伝導方程式の導出」
が丁寧で分かりやすい。

[2] 山崎郭滋, 「偏微分方程式の数値解法入門」, 森北出版株式会社，1993.

---

#補遺

1. 2次元熱伝導方程式もクランク-ニコルソン法で解けるが，連立一次方程式を解く回数が多くなる。空間グリッド数を$Ns$, 時間グリッドを$Nt$とすると，$Ns$次元熱伝導方程式を解くためにはおよそ$Nt \times Ns^N$回連立一次方程式を解く必要があり， 次元数の増加に伴い，クランク-ニコルソン法による陰解法は計算コストが著しく増加する。 計算コストを軽減する方法の一つに**交互方向陰解法(Alternating Direction Implicit method, ADI法)**がある。

2. 放物型偏微分方程式の物理学で出てくる例は熱伝導方程式の他にも，拡散方程式や時間に依存するシュレディンガー方程式などがある。