numpy, sympy, scipyを利用して,
1階常微分方程式を初期条件の下で解く。
問題:
$x'(t)+k x(t)=0$, 初期条件 $x(0)=1$, (k=1はパラメータ)
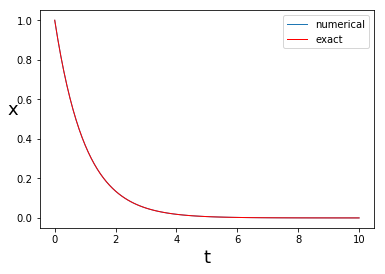
厳密解は$x(t)=e^{-t}$である。
from sympy import * # sympyライブラリから全ての機能をimoprt
import numpy as np # numpyをnpという名前でimport
from scipy.integrate import odeint
import matplotlib.pyplot as plt
"""
例題: 1階常微分方程式:
dx/dt = -kxを x(0)=1の初期条件の下で解く
"""
x=Symbol('x') # 文字 'x'を変数xとして定義
y=Symbol('y') # 文字 'y'を変数yとして定義
t=Symbol('t') # 文字 't'を変数yとして定義
k=Symbol('k')
def func(x, t, k): # dx/dtを関数として定義
dxdt=-k*x
return dxdt
k = 1.0 #パラメータへ値を設定する
x0 = 1.0 # 初期条件
t=np.linspace(0,10,101) # 積分の時間刻み設定: 0から10までを101等分する
sol=odeint(func, x0, t, args=(k,)) # 数値的に微分方程式を解く。結果をsolというリストへ格納する。
# 比較のための厳密解(e^-t)をリストexact_solへセット
exact_sol=[]
tt=np.linspace(0,10,101)
for i in tt:
exact_sol.append(exp(-1.0*float(i)))
#
# 可視化
plt.plot(t, sol, linewidth=1,label='numerical') # 数値解
plt.plot(tt, exact_sol, color='red',linewidth=1, label='exact') #真の解
plt.xlabel('t', fontsize=18)
plt.ylabel('x', fontsize=18,rotation='horizontal')
plt.legend(loc='upper right')
plt.show()