[Pythonによる科学・技術計算] 2次元ランダムウォーク(酔歩問題), 数値計算

乱数を利用した2次元ランダムウォークのシミュレーションを行う。

1ステップを1とし， 原点(0,0)からスタートして二次元平面上をランダムウォークする。

import numpy as np
from random import random
import matplotlib.pyplot as plt
from math import *
"""
2次元ランダムウォーク
"""

N_calc_list = [10]
x, y, r = 0, 0, 0
R_list=[]

N=100000

x_list=[0]
y_list=[0]
for n in range(N):
    theta=2.0*pi*random()#角度θ(2pi単位)をランダムにするため，random()を使って[0,1]の一様乱数を発生させる。
    x = x+cos(theta) # x方向への移動。cos(θ)。
    y = y+sin(theta) # y方向への移動。sin(θ)
    x_list.append (x) # xの値をx_listに格納していく
    y_list.append(y) # yの値をx_listに格納していく
   
# for plot
plt.plot( x_list,y_list) # (x,y)のプロット
plt.xlabel('X ') # ｘ軸のラベル
plt.ylabel('Y') # y軸のラベル
plt.xlim([-120,120])  # x軸の範囲
plt.ylim([-120,120]) # y軸の範囲
plt.show()

##結果

(0,0)をスタート位置とし，100000歩移動の軌跡

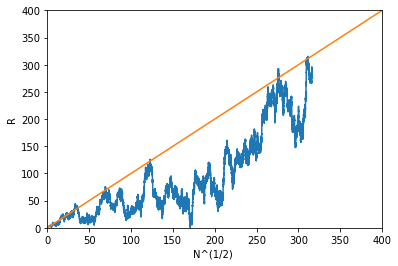
原点(0,0)からの距離Rと移動ステップ数Nの関係。x軸を$N^{1/2}$でプロットしている。オレンジ線は$N^{1/2}->∞$でえられる理論値。