Go to Qiita Advent Calendar Top
LoginSignup
16
18

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@sci_Haru(Haru_M D)

[Pythonによる科学・技術計算] 温度一定のやさしい分子動力学シミュレーション, 速度スケーリング法，2次元系, NVTアンサンブル，熱・統計物理学

Last updated at Posted at 2017-09-27

はじめに

[Pythonによる科学・技術計算]初歩的な分子動力学シミュレーション, 2次元系, NVEアンサンブル，熱・統計物理学

では，粒子数(N)，体積(V)とエネルギー(E)が一定の系の分子動力学(MD)シミュレーション(NVE MD)を行う簡易コードを作成しました。
得られる温度・圧力はシミュレーション過程で常に変動していました(熱的な"揺らぎ"が生じています)。
非平衡現象を考える場合はこのようなシミュレーションが有効です。

しかし，理・工学の多くの研究分野で温度(や圧力)が一定である条件下で実験や理論計算が行われています。
温度が一定下でのMDシミュレーション(NVT MD)を行うことに意義が見いだされます。

そこで本記事では温度一定のMDシミュレーションを行うための簡便な手法である"速度スケーリング法"を実装し，それをMDシミュレーションの典型的な応用例の一つである状態方程式計算へと応用します。

内容

1. 速度スケーリング法
2. 計算コード
3. 結果: 低温・高温シミュレーションの実施: アニメーション
4. 状態方程式: 一定体積下における圧力と温度の関係

どんな人向け？

  1. MDシミュレーションに興味がある方
  2. 温度制御の初歩について興味がある方
  3. とにかく原子が動く様子をみたい方

速度スケーリング法による一定温度シミュレーション

温度を一定にするため，MDシミュレーションの各時間ステップで速度を，"温度Tの熱平衡状態にある系の速度"になるように修正します。すべての粒子の速度を強制的に一斉にスケーリングするのです。そのためのスケーリング係数$\alpha$として，

$$\alpha =(\frac{\eta k_B T}{2 KE})^\frac{1}{2} \tag 1 $$

とします。ここで，$k_B$はボルツマン定数，KEは系の運動エネルギーの総和で，$ KE = \sum_i (m V_i^2)/2$となります。
また$\eta$は，系の自由度で，粒子数を$N$として$\eta = 2N$ (2次元), $\eta = 3N$ (3次元)となります(厳密には系に課された拘束条件によってわずかに異なる値を用いるべきですが，慣習としてこれらの値が使われることが多いようです)。

この$\alpha$を用いて，各粒子iの速度V_iを

$$V_i'= \alpha V_i \tag 2$$

として$\alpha$倍します。

この$V'$を用いて運動エネルギーKE'を計算すれば，

$$ KE' = \sum_i (m V_i'^2)/2 = \frac{\eta k_B T}{2} \tag 3$$

となります。つまり，このスケーリングによって熱平衡状態において温度がTとなるような速度分布が得られます。
これがポイントです。

十分に長い時間MDシミュレーションを行えば，系の微視的状態はこのとき統計力学でいうところの"正準分布"となります。

計算コード

基本的には[1]と同様です。
毎MD時間ステップで速度スケーリングを施しています。
温度は低温 T=1(100度相当)と高温T=10(1000度相当)の2パターンで計算しました。


"""
NVT MDシミュレーション
2次元
レナード-ジョーンズポテンシャル
速度スケーリング法
Sept. 2017
"""
%matplotlib nbagg

import numpy as np
import random
import matplotlib.pyplot as plt
import matplotlib.animation as animation


fig = plt.figure(figsize = (8, 6))
ims = []


lat_x = 0.691 # 格子定数: x
lat_y = 0.691
Lx = 5 # 格子点: x
Ly = 5 
N_atom = Lx*Ly
m=1 # 質量

delta_t = 0.002

T_const = 1  #  無次元量
# T_const = T_const /119 # convert to natural unit


# 粒子生成

Max_step =600

x = np.zeros([N_atom],float)
y = np.zeros([N_atom],float)

vx = np.zeros([N_atom],float)
vy = np.zeros([N_atom],float)

fx = np.zeros([N_atom,2],float)# Q: What is this "2"?
fy = np.zeros([N_atom,2],float)   
# L = int(np.sqrt(N_atom))

# step毎の物理量の格納
T_lis = []
P_lis =  []
KE_lis =[]
PE_lis =[]
Eot_lis =[]
Tav_lis = []
Pav_lis =  []
KEav_lis =[]
PEav_lis =[]
Eotav_lis =[]
##

density = N_atom/(Lx*Ly*lat_x*lat_y) # 数密度: 2次元

print ("number density = ", density)


def Maxwell_velocity2D(TT): # マクスウェルの速度分布から: ボックス-ミュラー法: self 
    for i in range(N_atom):
        R1=random.random()
        R2=random.random()
        R3=random.random()
        R4=random.random()
        vx[i] = (np.sqrt(-2* (TT/m)*np.log(R1)))*np.cos(2*np.pi*R2)
        vy[i] = (np.sqrt(-2* (TT/m)*np.log(R3)))*np.cos(2*np.pi*R4)

def initialposMaxwellvel():
    i=-1
    for ix in range(Lx):
        for iy in range(Ly):
            i += 1
            x[i] = lat_x*ix
            y[i] = lat_y*iy
    
    Maxwell_velocity2D(T_const)

 #速度スケーリング法による温度制御

def velocity_scaling(KE):
    dim = 2
    aa = dim*N_atom # 自由度: 
    fac_T=np.sqrt(aa*T_const/(2*KE))
    
    vx[:] = fac_T*vx[:]
    vy[:] = fac_T*vy[:]
    


def sign(a,b):
    if b >= 0:
        return abs(a)
    else:
        return -abs(a)
    
def Forces(t,w,PE,PEorW):
    rcut = 4#カットオフ
    PE = 0
    
    r2cut = rcut**2
    
    
    fx[:,t] = 0
    fy[:,t] = 0
    for i in range(N_atom-1):
        for j in range(i+1, N_atom):
            dx = x[i] - x[j]
            dy = y[i] - y[j]
                
                # 近接 イメージ相互作用
            if (abs(dx) > 0.5*lat_x*Lx):
                dx = dx - sign(lat_x*Lx,dx)
            if (abs(dy) > 0.5*lat_y*Ly):
                dy = dy-sign(lat_y*Ly,dy)
            r2 = dx**2+dy**2
                
            if (r2 < r2cut):
                if r2 == 0 :
                    r2 = 0.0001
                invr2 = 1/r2
                    
                wij = 48*(invr2**3-0.5)*(invr2**3)
                fijx = wij*invr2*dx
                fijy = wij*invr2*dy
                    
                fx[i,t] += fijx
                fy[i,t] += fijy
                fx[j,t] -= fijx
                fy[j,t] -= fijy
                    
                PE += 4*(invr2**3)*((invr2**3)-1)
                w += wij
    if (PEorW == 1) :
        return PE
    else :
        return w
         
# メイン: 時間発展
def time_evolution():
    
    avT = 0
    avP = 0
    Pavg = 0
    avKE=0
    avPE=0
    
    t1 = 0
    PE = 0.0
    
    
    # 初期化
    KE = 0
    w = 0
    
  
  #  initialposvel()
    initialposMaxwellvel()
    KE = (np.sum(vx**2)+np.sum(vy**2))/2
    
    #速度スケーリングによる温度一定化
    velocity_scaling(KE)
    KE = (np.sum(vx**2)+np.sum(vy**2))/2
    
    T = KE/N_atom
    P = density*(2*KE+1.5*w)/(3*N_atom) # 圧力の計算: for 2D
 
    PE = Forces(t1, w, PE, 1)
    time = 1   
    n_step=0

    
    
    while n_step < Max_step:
        if n_step % 50 ==0: 
            print ("step=",n_step)
            print("T=",T," KE/N = ",KE/N_atom," PE/N = ",PE/N_atom," Etot/N = ",(KE+PE)/N_atom, " P=",P)


        if n_step % 5 ==0:
            im=plt.scatter(x, y, s=240, c="pink", alpha=0.9, linewidths="1.5",edgecolors="black")
            ims.append([im])      

        n_step += 1
  

            
        for i in range(N_atom):   # 
            PE = Forces(t1, w, PE, 1)    
            # 速度ベルレー法による更新
            x[i] +=delta_t*(vx[i]+delta_t*fx[i,t1]/2)
            y[i] +=delta_t*(vy[i]+delta_t*fy[i,t1]/2)

            if x[i] <= 0: 
                x[i] += lat_x*Lx
            if x[i] >= lat_x*Lx:
                x[i] -= lat_x*Lx
            if y[i] <= 0:
                y[i]  += lat_y*Ly
            if y[i] >= lat_y*Ly:
                y[i] -= lat_y*Ly
          

                
        PE = 0.
        t2=1
        PE = Forces(t2, w, PE, 1)
        
        KE = 0.
        w = 0.



            #for i in range(N_atom):
        # 速度ベルレー法による更新
        vx[:] += delta_t*(fx[:,t1]+fx[:,t2])/2
        vy[:] += delta_t*(fy[:,t1]+fy[:,t2])/2
        
        KE =(np.sum(vx**2)+np.sum(vy**2))/2
        
        w = Forces(t2, w, PE, 2)
        
        velocity_scaling(KE)
        KE = (np.sum(vx**2)+np.sum(vy**2))/2
        T = KE/N_atom
        
        #        P = density*(KE + w)
        P = density*(2*KE+1.5*w)/(3*N_atom) #  for 2D
        
        
        
        
        #平均値
        avT += T
        avP += P
        avKE += KE
        avPE += PE
        time +=1
        t = time
        if (t == 0):
             t = 1
         
        # 時間平均
        Pavg =avP/t
        eKavg = avKE/t
        ePavg = avPE/t
        Tavg = avT/t
        
        T_lis.append(T) # 
        P_lis.append(P)  # P
        KE_lis.append(KE/N_atom)
        PE_lis.append(PE/N_atom)
        dumEtot = KE+PE
        Eot_lis.append( dumEtot /N_atom)
        
        Tav_lis.append(Tavg )# 
        Pav_lis.append(Pavg) 
        KEav_lis.append(eKavg/N_atom)
        PEav_lis.append(ePavg/N_atom)
        Eotav_lis.append((eKavg+ePavg)/N_atom)
    
        
        
       
##

time_evolution()

plt.axis([0,lat_x*Lx,0,lat_y*Ly])
ani = animation.ArtistAnimation(fig, ims, interval =1)
plt.show() 
# ani.save("output.gif", writer="imagemagick")

print("P_th=",Pav_lis[-1], "E_th/N_atom =", Eotav_lis[-1])

グラフ作成のためのコード



%matplotlib inline

import matplotlib.pyplot as plt
plt.close()


step=list(range(len(Eot_lis)))

# plt.plot(step, KE_lis,'-', color='red', linewidth = 1, aa=True,label='KE/N')
# plt.plot(step, PE_lis,'-', color='blue',linewidth = 1, aa=True,label='PE/N')


# plt.plot(step, KEav_lis,'-', color='red', linewidth = 1, aa=True,label='KE/N')
# plt.plot(step, PEav_lis,'-', color='blue',linewidth = 1, aa=True,label='PE/N')
plt.plot(step, Eot_lis,'--', color='black', linewidth = 1, aa=True,label='Etot/N')
plt.plot(step, Eotav_lis,'-', color='black', linewidth = 2, aa=True,label='Etot/N')

plt.legend(loc='best')
plt.xlabel('MD steps') # ｘ軸のラベル
plt.show()

plt.close()
plt.plot(step, T_lis,'-', color='purple', linewidth = 2, aa=True,label='T (K)')
# plt.plot(step, Tav_lis,'-', color='purple', linewidth = 1, aa=True)

plt.legend(loc='best')
plt.xlabel('MD steps') # ｘ軸のラベル

plt.show()



plt.close()

plt.plot(step, P_lis,'--', color='brown', linewidth = 1, aa=True, label='P')
plt.plot(step, Pav_lis,'-', color='brown', linewidth = 2, aa=True, label='P_average')
plt.legend(loc='best')
plt.xlabel('MD steps') # ｘ軸のラベル

plt.show()

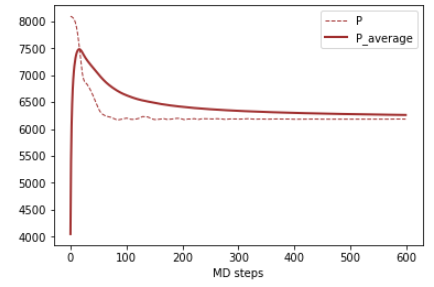
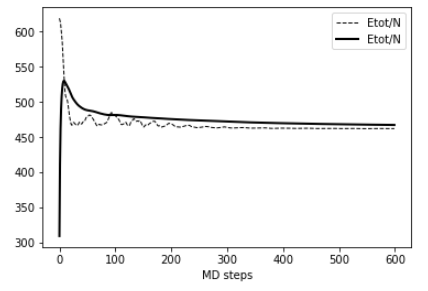
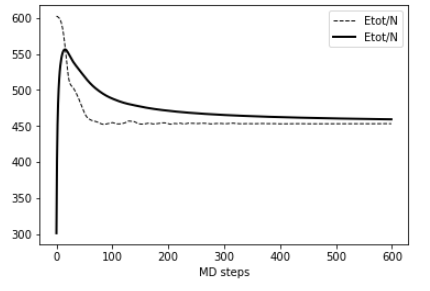
結果(1):低温: T=1 (マイナス200度に相当)

温度等をモニタリングした結果を示します。
速度スケーリング法により，温度(T)が常に一定に保たれていることが分かります。
一番左から，温度(T)，運動エネルギー(KE)，ポテンシャルエネルギー(PE)，全エネルギー(Etot)，圧力(P)となります。

step= 0
T= 1.0  KE/N =  1.0  PE/N =  600.73642218  Etot/N =  601.73642218  P= 1.39621611471
step= 50
T= 1.0  KE/N =  1.0  PE/N =  455.868076112  Etot/N =  456.868076112  P= 6229.32029634
step= 100
T= 1.0  KE/N =  1.0  PE/N =  451.940825042  Etot/N =  452.940825042  P= 6177.9196658
step= 150
T= 1.0  KE/N =  1.0  PE/N =  451.709608203  Etot/N =  452.709608203  P= 6174.97098122
step= 200
T= 1.0  KE/N =  1.0  PE/N =  452.415687627  Etot/N =  453.415687627  P= 6184.69738263
step= 250
T= 1.0  KE/N =  1.0  PE/N =  452.62157811  Etot/N =  453.62157811  P= 6188.96942751
step= 300
T= 1.0  KE/N =  1.0  PE/N =  452.445308226  Etot/N =  453.445308226  P= 6186.38712653
step= 350
T= 1.0  KE/N =  1.0  PE/N =  452.165676806  Etot/N =  453.165676806  P= 6182.24942277
step= 400
T= 1.0  KE/N =  1.0  PE/N =  451.999830418  Etot/N =  452.999830418  P= 6179.69781538
step= 450
T= 1.0  KE/N =  1.0  PE/N =  451.923782704  Etot/N =  452.923782704  P= 6178.82790637
step= 500
T= 1.0  KE/N =  1.0  PE/N =  451.973556048  Etot/N =  452.973556048  P= 6179.77975555
step= 550
T= 1.0  KE/N =  1.0  PE/N =  452.080984437  Etot/N =  453.080984437  P= 6181.30940397

次に，原子の運動の様子を見てみます。

原子は安定位置周りで振動している固体状態となっていることがわかります。

output_MD_USE_for_Qiita_NVT.gif

NVTアンサンブルではエネルギー・圧力が揺らぎます。その平均値が，通常，観測値とされる"熱平均値"です。
系は100ステップあたりから熱平衡状態になっています。
スクリーンショット 2017-09-27 17.44.07.png

スクリーンショット 2017-09-27 17.44.11.png

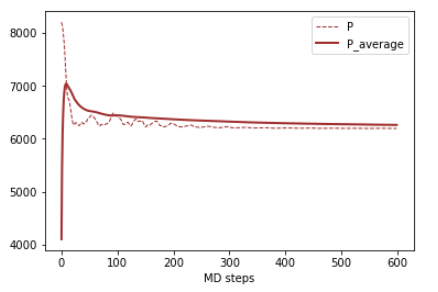
結果(2): 高温: T=10 (1000度に相当)

原子は安定位置から移動(拡散)しています。これは液体状態です。
output_MD_USE_for_Qiita_NVT.gif

スクリーンショット 2017-09-27 18.08.18.png
スクリーンショット 2017-09-27 18.08.21.png

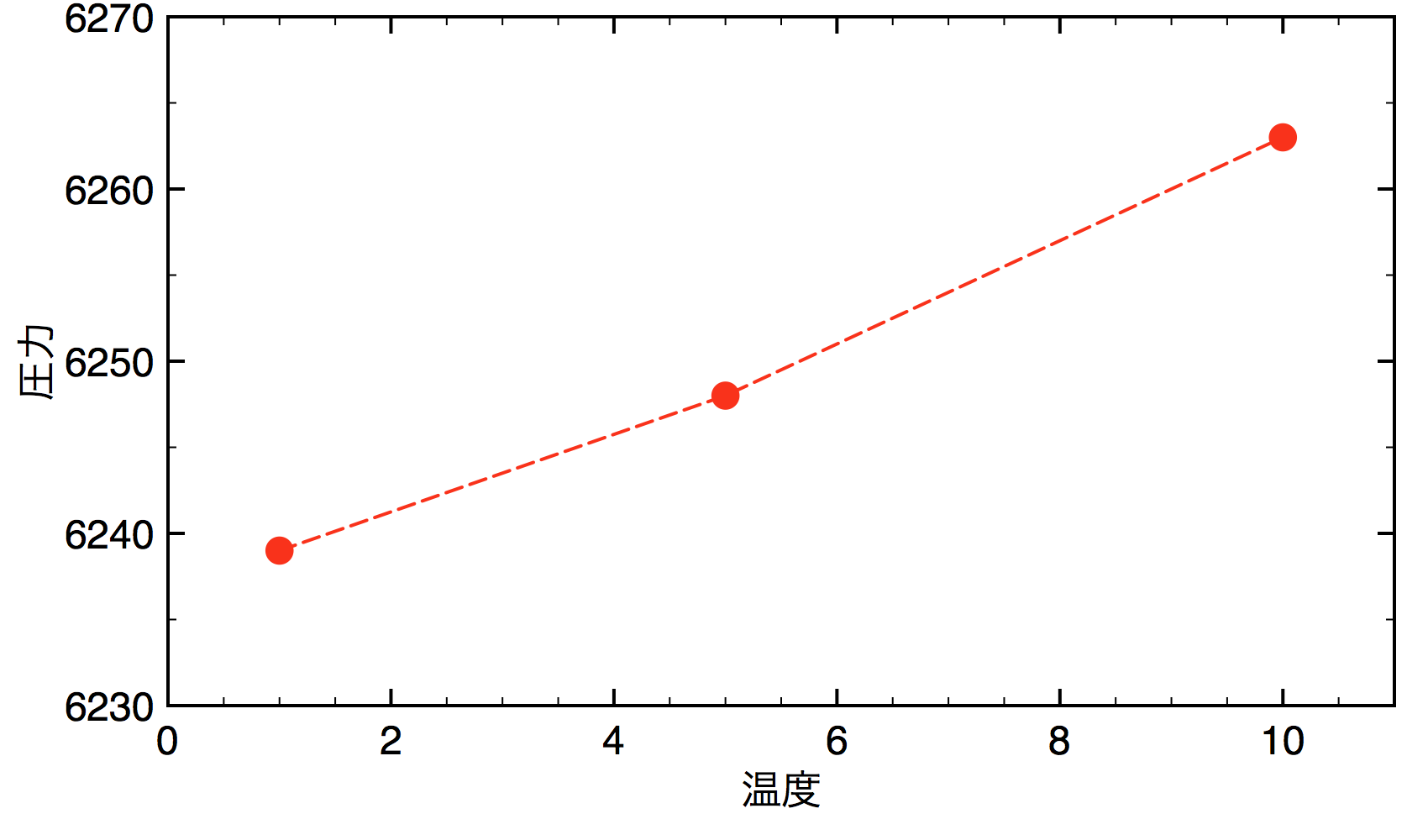
状態方程式

温度を変えた二つのシミュレーションから，熱平衡状態の圧力がそれぞれ，
T = 1 P = 6239
T = 5 P = 6248
T = 10 P = 6263

と変化することがわかります。
体積一定の下で温度を増加させると系の圧力が増加することを意味しています。この圧力を熱圧力といいます。

t.png

図. 一定体積下における温度と圧力の関係。

このように，体積を変えて同様のシミュレーションを繰り返すことにより，
温度・圧力・温度についての関係式すなわち状態方程式を決定することが可能です。

また，加温に伴う固体から液体への変化の例でも見たとおり，
温度等を変化させることで物質の状態の変化をシミュレートできます。つまり，相転移のシミュレートも可能です。

これらは分子動力学法の理・工学への典型的な応用例です。

補遺

  1. 速度スケーリング法の運動学的な妥当性に関しては述べませんでしたが，速度スケーリング法は解析力学の立場から基礎付けることが可能です。それに基づくと，速度スケーリング法によるMDシミュレーションは，外界とのエネルギーの授受を考慮した一般化力つきのラグランジュ方程式に従う粒子の(仮想的な)ダイナミクスを行っていることに相当することが分かります。詳しくは[2]を御覧ください。

  2. 本稿で用いた速度スケーリング法の他にも，温度を一定に保つための種々の方法が提案されています。特に，拡張系法の一つである**能勢＝フーバー・サーモスタット**は一定温度MDシミュレーションを行うための高精度・高効率手法として知られています。興味がある方は[3]を参照してください。

参考文献

[1] [Pythonによる科学・技術計算]初歩的な分子動力学シミュレーション, 2次元系, NVEアンサンブル，熱・統計物理学

[2] 神山新一・佐藤明，『分子動力学シミュレーション』，朝倉書店，1997.

[3] 能勢修一，[『計算物理学特論 分子動力学シミュレーション・数値積分法』] (http://www.phys.keio.ac.jp/guidance/labs/riron/pdf/nosenote1.pdf) (<-- webにあります)

16
18
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
16
18

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?