[Pythonによる科学・技術計算] 1次元-3次元離散高速フーリエ変換, scipy

#はじめに
フーリエ変換は科学・技術研究を遂行するうえで必要不可欠な技術である。本稿ではscipyのscipy.fftpackモジュール[1]を用いた高速離散フーリエ変換の方法をやさしい例題を通じてまとめておく。
通常の離散フーリエ変換の方法については，初等的なテキストがあるので適宜文献を参照されたい[2,3]。

なお，本稿では仕事現場での利用シーンを考えてscipyの高速フーリエ変換ライブラリの利用を前面に出している[4]。例題(1)の動作確認をしつつ練習すればすぐに現場で使えるようになると思う。

#内容

(1) 1次元離散フーリエ変換の例
(2) 3次元フーリエ変換の例

---

#例題(1): 1次元離散フーリエ変換

この例題ではガウス関数$f(t)= e^{(-(t-5)^2)}$のフーリエ変換 $g(\omega)$を求める。
使うメソッドは下記の二つだけ。

1. scipy.fftpack.fft フーリエ変換
2. scipy.fftpack.ifft 逆フーリエ変換

データ総数Nを40，サンプリングの幅Tが$t=0$から$t=10$まで ($T=10$)とする。

したがって時間のサンプリングは

$t_n \ = \frac{nT}{N} (n =0, 1, ..., N-1)$

となる。

それに伴い，振動数$\omega$の離散点は

$\omega_k = \frac{2k\pi}{T} (k=1,2,3,...,N)$

となる。

プログラムの流れは以下のとおりである。

1. ガウス関数$f(t)= e^{(-(t-5)^2)}$をt=0から10まで一様に40点サンプリングする。
2. fftを使ってそれを複素離散フーリエ変換して$g(\omega_n)$を得る。
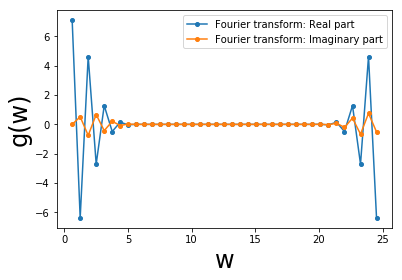
3. それを可視化する(図１)。実部と虚部にわけている。
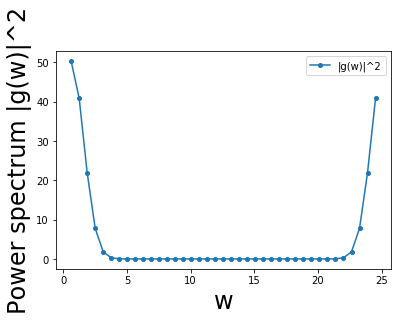
4. パワースペクトル$|g(\omega_n)|^2$を計算・図示する(図2)。
5. $g(\omega_n)$をもう一度フーリエ変換し(逆フーリエ変換), $ff(t)$という関数をえる。
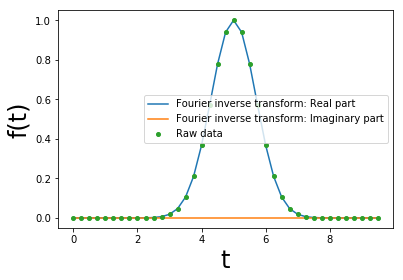
6. $ff(t)$と$f(t)$を比較する(図3)。与えたデータ点を厳密に再現する。

$f(t)$の関数形を変えることで望みの関数の高速フーリエ変換が可能である。

FFT1D.py

""" 
1次元 離散フーリエ変換
"""
import numpy as np
from scipy.fftpack import fft, ifft
import matplotlib.pyplot as plt


# 時系列のサンプルデータの作成
N = 40                      # データ数
T=10            # サンプリング幅
del_t= T/N   #  サンプリング間隔

del_w=2*np.pi/T # 離散フーリエ変換の振動数の間隔
#

# 離散点　生成
t = np.arange(0,T-del_t,del_t)
w=np.arange(2*np.pi/T, 2*np.pi*N/T, del_w)

#

f = np.exp(-(t-5)**2) # # サンプルデータを与える関数

#
g = fft(f)

g_real=np.real(g)
g_imag=np.imag(g)

#plot
plt.xlabel('w', fontsize=24)
plt.ylabel('g(w)', fontsize=24)

plt.plot(w,g_real,marker='o', markersize=4,label='Fourier transform: Real part')
plt.plot(w,g_imag,marker='o',markersize=4, label='Fourier transform: Imaginary part')

plt.legend(loc='best')

plt.show()


# パワースペクトルの表示

plt.plot(w,np.abs(g)**2,marker='o',markersize=4,label='|g(w)|^2')

plt.xlabel('w', fontsize=24)
plt.ylabel('Power spectrum |g(w)|^2', fontsize=24)
plt.legend(loc='best')

plt.show()


# 逆離散フーリエ変換

ff = ifft(g)
plt.plot(t, np.real(ff), label='Fourier inverse transform: Real part')
plt.plot(t, np.imag(ff), label='Fourier inverse transform: Imaginary part')

plt.plot(t, f,'o',markersize=4,label='Raw data')


plt.xlabel('t', fontsize=24)
plt.ylabel('f(t)', fontsize=24)
plt.legend(loc='best')

plt.show()

#結果(1) 1次元高速離散フーリエ変換

図1. 離散フーリエ変換$g(\omega_n)$

図２. パワースペクトル$|g(\omega_n)|^2$

図3. 逆複素フーリエ変換したもの(線)とサンプリングデータ(緑丸)との比較。実関数を考えていたので，逆複素フーリエ変換の虚部はゼロになっている。

---

#例題(2) ３次元高速離散フーリエ変換

この例題では3次元のガウス関数 $f(t_x,t_y,t_z)= e^{-[(t_x-5)^2+(t_y-5)^2+(t_z-5)^2)]}$の高速複素離散フーリエ変換を行っている。
1次元問題だった例題(1)と比べて，添え字等が増えるが，内容的に大きく難化するものではない。

多次元(2以上)のときに使うメソッドも一次元のときと同様，下記の二つだけである。

1. scipy.fftpack.fftn n次元フーリエ変換
2. scipy.fftpack.ifftn n次元逆フーリエ変換

フーリエ変換の次元は，フーリエ変換を行うさいの配列のサイズからscipyが勝手に判別してくれるのでプログラマ側はあまり神経質になる必要はない

この例題では動作確認だけを意図しており，可視化は行っていない。しかし必要になれば容易に望みのプロットが可能であろう。

プログラムの流れは以下のとおりである。

1. ガウス関数$f(t_x,t_y,t_z)= e^{-[(t_x-5)^2+(t_y-5)^2+(t_z-5)^2)]}$を， "3次元の時間" $tx, ty, tz$をそれぞれt=0から10まで一様に4点サンプリングする(Nx, Ny, Nz=4,4, 4)。
2. fftnを使ってそれを複素離散フーリエ変換して$g(\omega_{x_n},\omega_{y_m},\omega_{z_k})$を得る。
3. ifftnを使って逆フーリエ変換し$f(t_x,t_y,t_z)$という関数をえる。
4. 数値を出力してみる。

""" 
多次元離散フーリエ変換
2017年 8月12日 
"""
import numpy as np
from scipy.fftpack import fftn, ifftn # n次元離散フーリエ・逆フーリエ変換 
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


# 時系列のサンプルデータの作成
Nx = 4        # Nx方向のデータ数
Ny = 4          # Ny方向のデータ数
Nz = 4          # Nz 方向のデータ数
Tx=10            # サンプリング幅
Ty = 10
Tz = 10

del_t_x= Tx/Nx   #  tx方向のサンプリング間隔
del_t_y= Ty/Ny   #  ty方向のサンプリング間隔
del_t_z= Tz/Nz   #  ty方向のサンプリング間隔


del_w_x=2*np.pi/Tx # 離散フーリエ変換のｘ成分の振動数の間隔
del_w_y=2*np.pi/Ty # 離散フーリエ変換のy成分の振動数の間隔
del_w_z=2*np.pi/Tz # 離散フーリエ変換のz成分の振動数の間隔

#
t_x, t_y, t_z= np.meshgrid(np.arange(0,Tx-del_t_x,del_t_x),np.arange(0,Ty-del_t_y,del_t_y), np.arange(0,Tz-del_t_z,del_t_z))  # メッシュ生成
w_x, w_y, w_z= np.meshgrid(np.arange(2*np.pi/Tx, 2*np.pi*Nx/Tx, del_w_x),np.arange(2*np.pi/Ty, 2*np.pi*Ny/Ty, del_w_y), np.arange(2*np.pi/Tz, 2*np.pi*Nz/Tz, del_w_z))  # メッシュ生成


#
f = np.exp(-((t_x-5)**2+(t_y-5)**2+(t_z-5)**2)) # サンプルデータを与える関数

#
g = fftn(f)  # 多次元高速フーリエ変換: 今の場合は3次元
g_real=np.real(g) # 実部
g_imag=np.imag(g) # 虚部


# 逆多次元離散フーリエ変換
ff = ifftn(g)
ff_real=np.real(ff)# 実部
ff_imag=np.imag(ff) #虚部

#結果(2): 3次元高速離散フーリエ変換

少し数値を出力してみる。

print(g[1,2,1])

out: (-0.500000003576+0.862688207649j)

フーリエ変換したgの[1,2,1]成分が-0.5+0.86i (複素数)，という意味である。

次にフーリエ逆変換したものをチェックしてみる。

print(ff[1,2,2])

out: (0.00193045413623+0j)

これは実数。問題なく計算できている。

---

#参考文献

1. scipyのscipy.fftpackモジュールのウェブページ
2. 金谷健一，「これなら分かる応用数学教室」，共立出版，2003.
3. ストラング， 「線形代数イントロダクション」，近代科学社，2015.
4. Mark Newman, "Computational Physics", Createspace Independent Publishing Platform, 2012.

"速くない"普通の離散フーリエ変換については多くの書籍やウェブサイトから情報を得ることができるだろう。文献2および3は高速フーリエ変換についても言及している。読者への配慮が行き届いており大変読みやすい。4は洋書だが本質をついた説明は一読の価値がある。