はじめに
matplotlibのArtistAnimationメソッドを用いて,
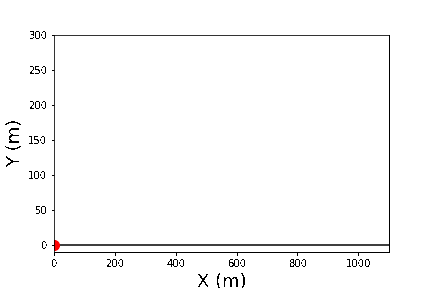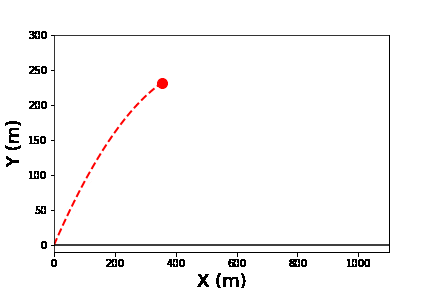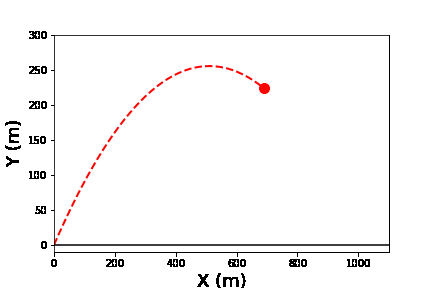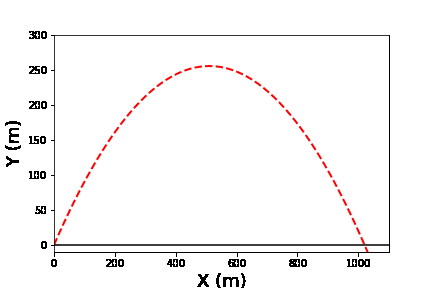
放物運動を行う物体の運動を軌跡も付けながら表示する。
ここでは軌跡部分と物体の運動部分の二つの絵を重ねて表示する方法を用いた。
誰もが考える単純で簡単な方法であるが,サッと可視化したいときには役に立つかもしれない。。
内容
$y$方向への一様な重力場中の角度$\theta$方向への鉛直投げ上げ問題である。
時刻 $t =0$のとき質点の位置を$(x_0,y_0)$, 初速度の大きさを$V_0$とすると,時刻$t$における質点の$x(t)$および$y(t)$座標は以下の通りになる。この質点の運動は放物線を描く。
$x(t) = x_0 + V_0 \ cos(\theta)$
$y(t)= y_0 + V_0 \ sin(\theta)-0.5\ \ g\ t^2$
本問題では $V_0 = 100$ m/s, $(x_0, y_0)=(0, 0)$, $\theta=\pi/4$ (=45度)と設定して質点の運動を描画する。
コード
"""
軌跡付きの放物運動のアニメーション
Animation with a locus
"""
import matplotlib.pyplot as plt
%matplotlib nbagg # Jupyter-notebookでアニメーションを表示する場合に付け加える
from matplotlib.animation import ArtistAnimation # アニメーション作成のためのメソッドをインポート
import numpy as np
fig = plt.figure()
anim = [] #アニメーション用に描くパラパラ図のデータを格納するためのリスト
tt = np.arange(0,15,0.5) # 描画するための時間設定: t=0から15までの0.5刻み。
x_all=[] # 全てのx位置のデータを格納するためのリスト
y_all=[] # 全てのy位置のデータを格納するためのリスト
# 初期条件の設定
V0 =100 # 初速度の大きさ: 100 m/s
theta=np.pi/4
x0=0 # 初期位置: x=0
y0=0 #初期位置: y = 0
g=9.8 # 重力定数 [m/s^2]
for t in tt:
x= [V0*np.cos(theta)*t+x0] # x(t)の記述
y = [-( g/2)*t**2+V0*np.sin(theta)*t+y0] # y(t)の記述
x_all.append(x[0]) # xの時々刻々データを格納
y_all.append(y[0]) # yの時々刻々データを格納
# 時刻tにおける質点と,時刻tに至るまでの運動の軌跡の二つの絵を作成し, アニメーション用のリストに格納する。
im=plt.plot(x,y,'o', x_all,y_all, '--', color='red',markersize=10, linewidth = 2, aa=True)
anim.append(im)
anim = ArtistAnimation(fig, anim) # アニメーション作成
# 描画のカスタマイズ
plt.xlabel('X',fontsize=18) #
plt.ylabel('Y',fontsize=18)
plt.xlim(0, 1100)
plt.ylim(-10,300)
plt.hlines([0], 0, 2000, linestyles="-") # y=0に線を描く。
fig.show()
anim.save("t.gif", writer='imagemagick') #アニメーションをt.gifという名前で保存し,gifアニメーションファイルを作成する。
結果
斜め45度方向へ初速100m/sで投げた場合の質点の運動のアニメーションを軌跡付きで表示したもの。
修正・変更ログ:
2017年8月3日: y(t)中の質量mを削除した。T_Shinajiさま,ご指摘ありがとうございました!
2017年8月10日: anim.save("t.gif")→ **anim.save("t.gif", writer='imagemagick')**へと変更した。 yoddyさま,ご指摘ありがとうございました!
参考文献
ArtistAnimationについては,
chez_sugi 氏のmatplotlibでアニメーション
を参考にさせていただきました。