はじめに
matplotlibを用いてベクトル場の可視化を行う。例として高校の物理学で学ぶ静電場および静磁場をプロットする。
どのプログラムも,流れとしては
- numpyのmeshgridメソッドで描画のためのx,yメッシュを作り,
- 生成された(x,y)点上でベクトル関数$F(u(x,y),v(x,y))$を定義し
- 様々なオプションをつけてメッシュ上に矢印(ベクトル)を描画する,
というものである。
具体例を見ながら動作を確認すると分かりやすいだろう。
内容
(1) 1つの点電荷が作る静電場の可視化
(2) 2つの点電荷(電気双極子)が作る静電場
(3) 原点を通る定常電流が作る静磁場
(4) 3次元ベクトル場 (原点においた点電荷が作る静電場)
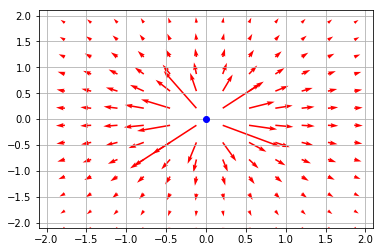
(1) 1つの点電荷が作る静電場の可視化
"""
(1) 原点にある1つの点電荷が作る静電場
"""
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
LX, LY=2.1,2.1 # メッシュのためのパラメータ
gridwidth=0.33
X, Y= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY,gridwidth)) # メッシュ生成
R = np.sqrt(X**2+Y**2) # 原点からの距離
# 点電荷の位置座標と電荷
X1,Y1=0,0 # 原点への電荷の配置
Q1=1 # 電荷量の設定
R1=np.sqrt((X-X1)**2+(Y-Y1)**2) # この電荷から任意点(X,Y)までの距離
plt.plot(X1,Y1,'o',color='blue') # 点電荷を描画
# ベクトル関数 F(U(x,y), V(x,y))を定義。静電場の表式を用いる。
U = Q1*(X-X1)/(R1**2)
V = Q1*(Y-Y1)/(R1**2)
plt.quiver(X,Y,U,V,color='red',angles='xy',scale_units='xy', scale=5.0) # ベクトル場をプロット
plt.xlim([-LX,LX]) # 描くXの範囲
plt.ylim([-LY,LY]) # 描くyの範囲
# グラフ描画
plt.grid()
plt.draw()
plt.show()
結果(1)
(2)2つの点電荷(電気双極子)が作る静電場
"""
(2) 2つの点電荷(電気双極子)が作る静電場
"""
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
LX, LY=2,2
gridwidth=0.2
X, Y= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY,gridwidth))
R = np.sqrt(X**2+Y**2)
# 2つの点電荷の位置座標と電荷
X1,Y1=1.1,0
Q1=1
R1=np.sqrt((X-X1)**2+(Y-Y1)**2)
plt.plot(X1,Y1,'o',color='blue')
X2,Y2=-1.1,0
Q2=-1
R2=np.sqrt((X-X2)**2+(Y-Y2)**2)
plt.plot(X2,Y2,'o',color='blue')
##
# ベクトル関数の設定。2電荷分。
U = Q1*(X-X1)/(R1**2)+Q2*(X-X2)/(R2**2)
V = Q1*(Y-Y1)/(R1**2)+Q2*(Y-Y2)/(R2**2)
plt.quiver(X,Y,U,V,color='red',angles='xy',scale_units='xy', scale=6.5)
plt.xlim([-LX,LX])
plt.ylim([-LY,LY])
# グラフ描画
plt.grid()
plt.draw()
plt.show()
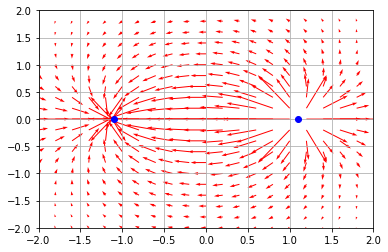
結果(2): 2つの点電荷(電気双極子)が作る静電場
(-1.1,0)と(1.1,0)におかれた二つの点電荷(電荷はそれぞれ1と−1)が作る静電場。
(3) 原点を通る定常電流が作る静磁場
"""
(3) 原点を通る定常電流が作る静磁場
"""
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
LX, LY=3,3
gridwidth=0.3
X, Y= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY,gridwidth))
R = np.sqrt(X**2+Y**2)
# 点電荷の位置座標と電荷
X1,Y1=0,0
I=1 #定常電流の値
R1=np.sqrt((X-X1)**2+(Y-Y1)**2)
plt.plot(X1,Y1,'o',color='blue')
# ベクトル関数の設定。定常電流が作る静磁場 F(U(x,y), V(x,y))
U = I*-1*(Y-Y1)/(R1)
V = I*(X-X1)/(R1)
plt.quiver(X,Y,U,V,color='red',angles='xy',scale_units='xy', scale=4.5)
plt.xlim([-LX,LX])
plt.ylim([-LY,LY])
# グラフ描画
plt.grid()
plt.draw()
plt.show()
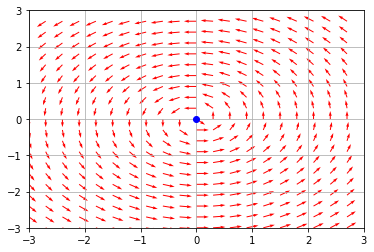
結果(3) 定常電流の作る静磁場
原点から紙面に垂直に続く定常一様電流Iが作る静磁場。
(4)3次元ベクトル場 (原点においた点電荷が作る静電場)
"""
(4) 3次元ベクトル場の図示
原点においた点電荷が作る静電場
"""
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D #3次元プロットのためのimport
import numpy as np
fig = plt.figure()
ax = Axes3D(fig)
LX, LY, LZ = 2,2,2 # xyzメッシュのパラメータ
gridwidth=0.9 #
X, Y, Z= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY,gridwidth),np.arange(-LZ, LZ, gridwidth) ) #メッシュ生成
R = np.sqrt(X**2+Y**2+Z**2)
# 点電荷の位置座標と電荷
X1,Y1, Z1=0,0,0
Q1=1
R1=np.sqrt((X-X1)**2+(Y-Y1)**2+(Z-Z1)**2)
ax.scatter3D(X1,Y1,Z1,"o", color='blue')
U = Q1*(X-X1)/(R1**2)
V = Q1*(Y-Y1)/(R1**2)
W= Q1*(Z-Z1)/(R1**2)
ax.quiver(X, Y, Z, U, V, W, color='red',length=1, normalize=False)
ax.set_xlim([-LX, LX])
ax.set_ylim([-LY, LY])
ax.set_zlim([-LZ, LZ])
plt.show()
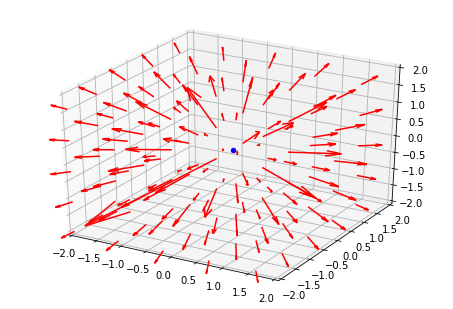
結果(4) 3次元ベクトル場 (原点においた点電荷が作る静電場)
原点に置かれた点電荷が作る電場の3次元プロット。