はじめに
最近オンラインで機械学習の授業を受けているのですが,学ぶことが多く,受けているだけだと忘れてしまいそうなので備忘録的にもここにまとめていく.
(全部英語なので日本語にまとめるだけでも勉強になりそう)
まだまだ勉強中の身なので,読んでて気になるところがあったらぜひコメントしてください.
まとめは24まで続く予定なので気長に更新していきます笑
この辺はまだ簡単なので正直まとめる必要はあまり感じてないのですが,何事も基本から,練習だと思ってつらつら書いていきます
オンライン授業について詳しく知りたい方はこちらから!
前回の復習
前回の授業では機械学習には学習方法,モデリング手法,アプローチなどに種類があること,
データモデリングには主に4つのブロックがあることをガウス分布を例にして説明してました.
線形回帰
今回は線形回帰というものについて考えていきます.
例題
例えば,こんなデータの分布が仮にあった時に
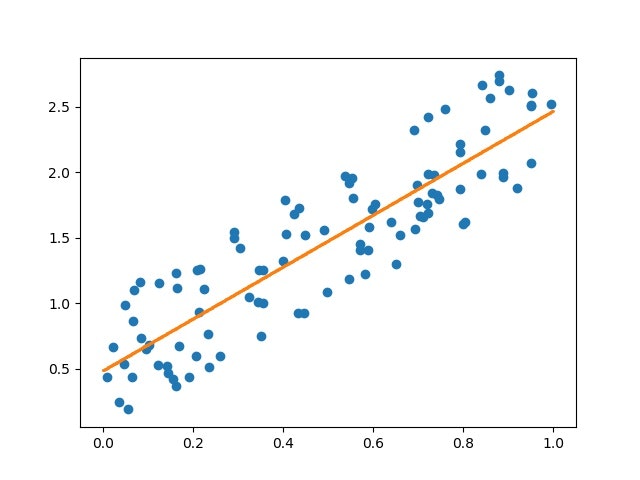
データは右肩上がりなので以下のように縦軸と横軸の関係を表せそうです
このオレンジ線の回帰モデルについては
縦軸をy,横軸をxとすると
y=w_0 + x~\times~w_1
と入力の線形結合で表すことができる.
ここで用いている$w_1$と$w_0$については得られたデータを元に学習している.
$w_1$は傾き(the slope).
$w_0$は切片(the intercept, bias, shift, offset)とか呼ばれる.
上の場合は一次元データで回帰モデルを作ったが,より高次元の特徴量を持つデータに対してもやり方は一緒で
(output) \approx w_0 + (input_1) \times w_1 + (input_2) \times w_2 ~...
という感じで入力とそれの係数が増る.ここでもやっぱり入力は線形結合
回帰問題とは
Data
Input : x \in \mathbb{R}^d ~~つまり得られたデータや特徴量や独立変数 \\
Output: y \in \mathbb{R} ~~~つまりレスポンスや従属変数
Goal
f:\mathbb{R}^d → \mathbb{R}
となる関数$f$,例えば,得られたデータ$(x,y)$に対して$y \approx f(x;w)$となるようなものを見つけること.
この関数$f$をregression functionという
線形回帰の定義
パラメータ$w$を持っていて,regression functionが線形な回帰手法を線形回帰という
最小二乗法
Model
線形回帰のモデルは
y_i \approx f(x_i;w) = w_0 + \sum_{j=1}^d x_{ij}w_{j.}
Model learning
訓練データとして$(x_1,y_1)...(x_n,y_n)$のデータセットを用いてモデルのパラメータ$w$を学習していく
そのためにパラメータが良いのか悪いのかを評価する関数が必要.
これが目的関数であり,最小二乗法では以下のようにして決定する
Least Squares
最小二乗の目的関数は訓練データの$y_i$とモデルから得られる$f(x;w)$の差が最小になるものが良いとする関数であり,以下のように表せる
w_{LS} = \underset{w}{\textrm{argmin}} \sum_{i=1}^n (y_i - f(x_i;w))^2 \equiv \underset{w}{\textrm{argmin}} ~L.
データの関係
ここで出てくるエラー{$y_i - f(x_i;w)$}を$\epsilon_i$としてズレを吸収すると,得られるデータの独立変数xと従属変数yの関係は以下のようになる
y_i = w_0 + \sum_{j=1}^d x_{ij}w_j + \epsilon_i
目的関数も
L = \sum_{i=1}^n \epsilon_i^2 = \sum_{i=1}^n (y_i - w_0 - \sum_{j=1}^d x_{ij}w_j )^2
と書き直せる.
これをさらに見やすくベクトルとして処理する
ベクトルとして処理
x_i = \begin{bmatrix}
1 \\
x_{i1} \\
x_{i2} \\
\vdots \\
x_{id}
\end{bmatrix}
として,それらを並べた$X$ベクトルを作る
X = \begin{bmatrix}
1 & x_{11} & \dots & x_{1d} \\
1 & x_{21} & \dots & x_{2d} \\
\vdots & & \vdots \\
1 & x_{n1} & \dots & x_{nd} \\
\end{bmatrix}
ただし,ランク落ちなどを考慮して
特徴量は連続値,次元数dはサンプル数nより小さいとする.つまりノッポな行列$X$となる.
1を行列に含めたのは$w_{0}$を重み行列の中に入れるためです.
重みベクトルを求める
重みベクトルの良し悪しは目的関数で決まるのでこれの形状を考えてみる.
二乗誤差であり,目的関数は$w$について2次関数かつ,下に凸の形をしてるので偏微分して極小値を考えればそこが誤差が最小になる$w$である.
よって
\nabla_w \textrm{L} = 0 \\
ただし
L = || y - Xw ||^2 = (y - Xw)^T (y - Xw) \\
なのでこれを用いて計算していくと
\nabla_w L = 2X^TXw -2X^Ty = 0 ~~~\Rightarrow ~~~ w_{LS}= (X^TX)^{-1}X^Ty
と求めることができる.
この$w_{LS}$が各訓練データのエラーを最小とする重みのベクトルである
prediction
もし新しいデータが得られた時にyを予測したい場合は
y_{new} = x_{new}^Tw_{LS}
で予測できる
最小二乗法の問題
重みベクトルを求める際に$(X^TX)^{-1}$を用いているが,これは$X^TX$がフルランクであることを前提条件としている
$X$は$n\times(d+1)$のマトリックスなので少なくとも$d+1$の線形独立な行が必要である.
(個人的には逆行列があるということは,得られたデータを表現するために$d+1$次元の空間が必要なイメージでいる)
つまり,データ数が少ないとランク落ちしてしまって逆行列がもとまらずに,答えが一つに求まらない.
線形回帰の拡張
今回のデータより複雑な分布をしているデータに対して,今までの1次の線形結合で構築したモデルでは十分な適応は得られないであろう.そこで多次元への拡張が必要になる
と言ってもデータを変更するだけ
もし,データが$x\in \mathbb{R},y \in \mathbb{R}$で得られる時,任意のp次元の多項式近似を行うとすると
X = \begin{bmatrix}
1 & x_1 & x_1^2& \dots & x_1^p \\
1 & x_2 & x_2^2& \dots & x_2^p \\
\vdots & & & \vdots \\
1 & x_n & x_n^2& \dots & x_n^p \\
\end{bmatrix}
これを最小二乗法で解くだけ.
ただpの値は人間が決め打ちするハイパーパラメータであり,pの値によっては過学習を起こす危険がある.
このマトリックスではp次の多次元に拡張しているだけだが,もちろん線形結合している限りにおいて,対数などその他の変換を行なっても良い.
まとめ
最小二乗法は回帰の結果と実際のデータの差を最小化するように各特徴量に重みを設定する方法
問題点もあるが,拡張の余地もある.重みの値でどの特徴量がよりレスポンスに影響を与えるのか考えられる.
参考
edX:CSMM.102x-Machine_Learning
https://www.edx.org/course/machine-learning-columbiax-csmm-102x-0