igraphとよばれるPythonのライブラリはグラフ構造(ソーシャルなあれとか)を書く為に翼利用されるらしいということを見かけたがいかんせん日本語の情報は少ない。
そこで公式ドキュメントのチュートリアル部分の解読をしてみようといった感じ
英語からの直訳チックの表現はご愛嬌と言った感じですかね。
グラフの生成
igraphのGraphインスタンスを作成
>>> g = Graph()
>>> g
<igraph.Graph object at 0x4c87a0>
頂点もエッジも0個である(U---頂点の個数 エッジの個数--)
>>> print g
IGRAPH U--- 0 0 --
頂点とエッジの追加
>>> g.add_vertices(3) #追加する頂点の個数
>>> g.add_edges([(0,1),(1,2)]) #追加するエッジ間の2頂点
頂点が無いところにエッジは追加できない
g.add_edges([(5, 0)])
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "/usr/lib/python2.7/dist-packages/igraph/__init__.py", line 255, in add_edges
return GraphBase.add_edges(self, es)
igraph._igraph.InternalError: Error at type_indexededgelist.c:272: cannot add edges, Invalid vertex id
以下適当に頂点とエッジを追加
>>> g.add_edges([(2,0)])
>>> g.add_vertices(3)
>>> g.add_edges([(2,3),(3,4),(4,5),(5,3)])
>>> print g
IGRAPH U---- 6 7 --
+ edges:
0--1 1--2 0--2 2--3 3--4 4--5 3--5
各エッジにはidが付されているのでそれを取得してみる
>>> g.get_eid(2,3)
3
idで指定してエッジを消してみる
>>> g.delete_edges(3)
g.delete_vertices()で頂点も消せる
エッジの数が減っていることの確認
summaryコマンドはエッジのprintを行わないので大規模グラフの確認の際はsummaryが推奨される
>>> summary(g)
IGRAPH U--- 6 6 --
グラフの生成2
igraphにはグラフ生成の各種関数があるのでそれらを用いてもグラフは作成できる
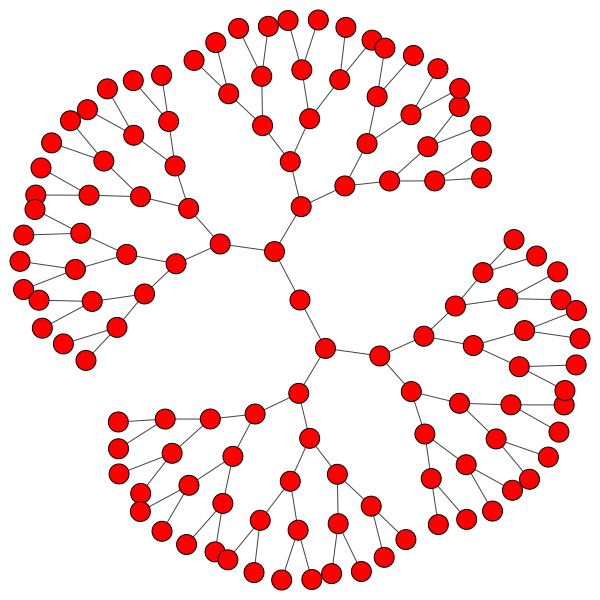
>>> g = Graph.Tree(127, 2)
>>> summary(g)
IGRAPH U--- 127 126 --
確率的に生成されてはいないことの確認
>>> g2 = Graph.Tree(127, 2)
>>> g2.get_edgelist() == g.get_edgelist()
True
エッジについて確認、source_vertex_id,target_vertex_id)で出力される
>>> g2.get_edgelist()[0:10]
[(0, 1), (0, 2), (1, 3), (1, 4), (2, 5), (2, 6), (3, 7), (3, 8), (4, 9), (4, 10)]
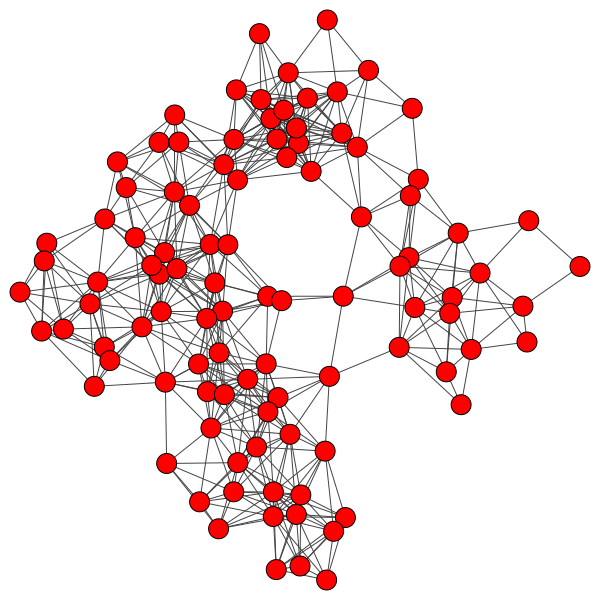
>>> g = Graph.GRG(100, 0.2)
>>> summary(g)
IGRAPH U---- 100 516 --
+ attr: x (v), y (v)
確率的に生成されているので同じパラで生成しても不一致
>>> g2 = Graph.GRG(100, 0.2)
>>> g.get_edgelist() == g2.get_edgelist()
False
isomorphic同型かどうかの確認関数
>>> g.isomorphic(g2)
False
属性の設定、取得
上記のグラフ構造ではグラフの頂点とIDを整数で決めたが、Pythonの辞書として各種値も登録できる
vs:vertex setting, es:edges setting 辞書として機能
あるキーに対して各頂点、各エッジのバリューをすべて定める必要がある
>>> g.vs
<igraph.VertexSeq object at 0x1b23b90>
>>> g.vs["name"] = ["Alice", "Bob", "Claire", "Dennis", "Esther", "Frank", "George"]
>>> g.vs["age"] = [25, 31, 18, 47, 22, 23, 50]
>>> g.vs["gender"] = ["f", "m", "f", "m", "f", "m", "m"]
>>> g.es["is_formal"] = [False, False, True, True, True, False, True, False, False]
ある頂点、エッジのバリューだけを変更することも可能である
>>> g.es[0]
igraph.Edge(<igraph.Graph object at 0x4c87a0>,0,{'is_formal': False})
>>> g.es[0].attributes()
{'is_formal': False}
>>> g.es[0]["is_formal"] = True
>>> g.es[0]
igraph.Edge(<igraph.Graph object at 0x4c87a0>,0,{'is_formal': True})
Edgeオブジェクトは各種属性を持っている
>>> g.es[0].source
0
>>> g.es[0].target
1
>>> g.es[0].index
0
Vertexオブジェクトも各種属性を持っている
>>> g.vs[1].index
1
>>> g.vs[1].attributes()
{'gender': 'm', 'age': 31, 'name': 'Bob'}
グラフ自体に辞書機能もある
>>> g["date"] = "2016-06-20"
>>> print g["date"]
2016-06-20
特定のキーに関する情報はdelコマンドで削除可能
>>> g.vs[3]["foo"] = "bar"
>>> g.vs["foo"]
[None, None, None, 'bar', None, None, None]
>>> del g.vs["foo"]
>>> g.vs["foo"]
Traceback (most recent call last):
File "<stdin>", line 25, in <module>
KeyError: 'Attribute does not exist'
グラフの構造的特性
各頂点から出ているエッジの数をリストで返してくれる
>>> g.degree()
[3, 1, 4, 3, 2, 3, 2]
一部の頂点に関してのみ考えることも可能
>>> g.degree(6)
2
>>> g.degree([2,3,4])
[4, 3, 2]
エッヂ間のつながりの尺度の各種計算関数
>>> g.betweenness()
[5.0, 0.0, 5.5, 1.5, 0.0, 2.5, 0.5]
>>> g.edge_betweenness()
[6.0, 6.0, 4.0, 2.0, 4.0, 3.0, 4.0, 3.0, 4.0]
>>> g.pagerank()
[0.1715187083669299, 0.07002553879920158,
0.20933537164407268, 0.16151684644322287,
0.11167544439518333, 0.16265174994590004,
0.11327634040548959]
一番つながりが強いエッジを探す
>>> ebs = g.edge_betweenness()
>>> max_eb = max(ebs)
>>> [g.es[idx].tuple for idx, eb in enumerate(ebs) if eb == max_eb]
[(0, 1), (0, 2)]
vsやesを用いても利用できる
>>> g.vs.degree()
[3, 1, 4, 3, 2, 3, 2]
>>> g.es.edge_betweenness()
[6.0, 6.0, 4.0, 2.0, 4.0, 3.0, 4.0, 3.0. 4.0]
>>> g.vs[2].degree()
4
属性に基づく頂点、エッヂに対するクエリ
頂点、エッヂの選択
>>> g.vs.select(_degree = g.maxdegree())["name"]
['Claire']
select:VertexSeqに対するメソッドでフィルター機能がある
positional、keyword を引数に取る
上の例ではpostional:_degree
引数postionalについて
positionalがNoneのとき返り値は空の列になる
>>> seq = g.vs.select(None)
>>> len(seq)
0
positionalが呼び出し可能なオブジェクト(i.e., a function, a bound method or anything that behaves like a function))ならすべての頂点で呼び出されることになり、関数がTrueを返せばその頂点は含まれ、違ければ、その頂点は排除される
>>> graph = Graph.Full(10)
>>> only_odd_vertices = graph.vs.select(lambda vertex: vertex.index % 2 == 1)
>>> len(only_odd_vertices)
5
positionalが反復可能なもの(i.e., a list, a generator or anything that can be iterated over)なら整数を返し、新たなインデックス番号が振られる(雑な表現)
>>> seq = graph.vs.select([2, 3, 7])
>>> len(seq)
3
>>> [v.index for v in seq]
[2, 3, 7]
>>> seq = seq.select([0, 2]) # filtering an existing vertex set
>>> [v.index for v in seq]
[2, 7]
>>> seq = graph.vs.select([2, 3, 7, "foo", 3.5])
>>> len(seq)
3s
positionalが整数なら、残りの引数も整数である必要があり、現在のvertex setのindexと考えられる
>>> seq = graph.vs.select(2, 3, 7)
>>> len(seq)
3
引数keywordについて(要加筆)
以下の表参照(nameの部分は各keyとして見る)
| keyword | 説明 |
|---|---|
| name_eq | 属性がkeywordと一致 |
| name_ne | 属性がkeywordと不一致 |
| name_lt | 属性がkeyword未満 |
| name_le | 属性がkeyword以下 |
| name_gt | 属性がkeywordより大きい |
| name_ge | 属性がkeyword以上 |
| name_in | 属性がkeywordに含まれる |
| name_notin | 属性がkeywordに含まれない |
特性に基づく一つの頂点、エッヂの検索
VertexSeq及びEdgeSeqはfindメソッドを持つ。
selectと似ているがfindは複数候補のうち最初の一つしか返してこない
>>> claire = g.vs.find(name="Claire")
>>> type(claire)
igraph.Vertex
>>> claire.index
2
もしマッチしなければエラーを吐く
>>> g.vs.find(name="Joe")
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: no such vertex
名前による頂点の検索
IDよりも名前の方が覚えやすいので、それを元に検索をするのは一般的である。
>>> g.degree("Dennis")
>>> g.vs.find("Dennis").degree() #上の行と同じこと
注:同じ名前をもつ頂点を作ることはできるが、nameで検索できるのは一つまでである(内部ではIDで区別されているのでIDを用いないとこの二者は区別がつかない)
レイアウトとプロット
レイアウトのアルゴリズム
レイアウトのアルゴリズムとはなんぞやと思っていたがぐぐってみるとどうやらグラフの描き方(配置の仕方ととらえたほうがいいのかもしれない)にも各種アルゴリズムが存在するらしく、それを指定するということらしい。
| Method name | short name | 説明 |
|---|---|---|
| layout_circle | circle, circular | 丸型のノードを配置する |
| layout_drl | drl | Distributed Recursive Layoutアルゴリズムを利用 |
| layout_fruchterman_reingold | fr | Fruchterman-Reingold force-directed アルゴリズムの利用 |
| layout_fruchterman_reingold_3d | fr3d,fr_3d | ↑を三次元に拡張 |
| layout_grid_fruchterman_reingold | grid_fr | ↑をgrid heuristics←??? |
| layout_kamada_kawai | kk | Kamada-Kawai force-directed アルゴリズムの利用 |
| layout_kamada_kawai_3d | kk3d,kk_3d | ↑を三次元に拡張 |
| layout_lgl | large, lgl, large_graph | Large Graph Layout アルゴリズムの利用 |
| layout_random | random | ランダムに配置 |
| layout_random_3d | random3d | ランダムに配置(三次元) |
| layout_reingold_tilford | rt,tree | |
| layout_reingold_tilford_circular | rt_circular tree | |
| layout_sphere | sphere, spherical, circular, circular_3d |