はじめに
3章までは、macOSの上でOpenGLの土台を用意し、三角形や立方体などの単純なモデルを用意して、基本的な描画を行うための知識を解説してきました。
4章からは、より複雑な3Dモデルを扱えるようにして、本格的な描画ができるようにステップアップしていきましょう。
この記事では、平行光源を1つ設置して、頂点シェーダでライティングの計算を行う、基本的なライティングの手法について解説します。まず1節で、シェーダを利用するプログラムと、GLSLによるシェーダ実装のデータの流れをおさらいしています。この説明が不要な方は、2節から読み進めてください。
1. シェーダ実装のおさらい
ライティングの実装に入る前に、いま一度、GLSLでのシェーダの実装と、シェーダを操作するためのプログラムについて復習しておきましょう。
1-1. GPU上にバッファを作りデータを登録する
カスタムシェーダを使って、OpenGLでデータを描画するためには、GPUのメモリ上にVBO, VAO, IBOという3種類の情報を登録する必要がありました。VBO → VAO → IBO の順番でバッファを生成し、データを登録することで、これら3種類のバッファが互いに関連付けられた状態で用意されます。
それぞれのバッファの役割は、次の通りです。
- VBOは頂点のデータを格納する。
- VAOはVBO内のデータ構造を格納する。
- IBOはメッシュごとに利用する頂点のインデックスを格納する。
これを行うコードは次のようになります。
// 構造体の用意
struct VertexData
{
GLKVector3 pos;
GLKVector4 color;
};
// 頂点データの用意
vector<VertexData> data;
data.push_back(...);
...
// インデックス・データの用意
vector<GLushort> indices;
indices.push_back(...);
...
// VBOの作成
GLuint vbo;
glGenBuffers(1, &vbo);
glBindBuffer(GL_ARRAY_BUFFER, vbo);
glBufferData(GL_ARRAY_BUFFER, sizeof(VertexData) * data.size(), &data[0], GL_STATIC_DRAW);
// VAOの作成
glGenVertexArrays(1, &vao);
glBindVertexArray(vao);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, sizeof(VertexData), &((VertexData *)0)->pos);
glVertexAttribPointer(1, 4, GL_FLOAT, GL_FALSE, sizeof(VertexData), &((VertexData *)0)->color);
// IBOの作成
glGenBuffers(1, &indexBuffer);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, indexBuffer);
glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(GLushort) * indices.size(), &indices[0], GL_STATIC_DRAW);
1-2. シェーダをコンパイルしてプログラムを生成する
次に、頂点シェーダとフラグメント・シェーダを個別にコンパイルして用意し、それらを組み合わせた「プログラム」と呼ばれるものを用意します。
この解説記事では、頂点シェーダとフラグメント・シェーダのソース・ファイルを同時に指定して、それを組み合わせたプログラムを、ShaderProgramクラスのオブジェクトとして扱ってきました。この部分のコードは、次の通りです。
ShaderProgram *program = new ShaderProgram("myshader.vsh", "myshader.fsh");
1-3. VAOを指定して描画を実行する
「VBO→VAO→IBO」の順番で作成したVBOとVAOとIBOは互いに関連付けられ、そのデータはVAOによって代表されます。描画する際には、VAOを指定して glDrawElements() 関数を呼び出せば、関連付けられたIBOのインデックス・データに従って、VBOから頂点ごとの各種のデータが頂点シェーダへとストリームされていきます。
ここまでの流れを、図にしてまとめてみましょう。
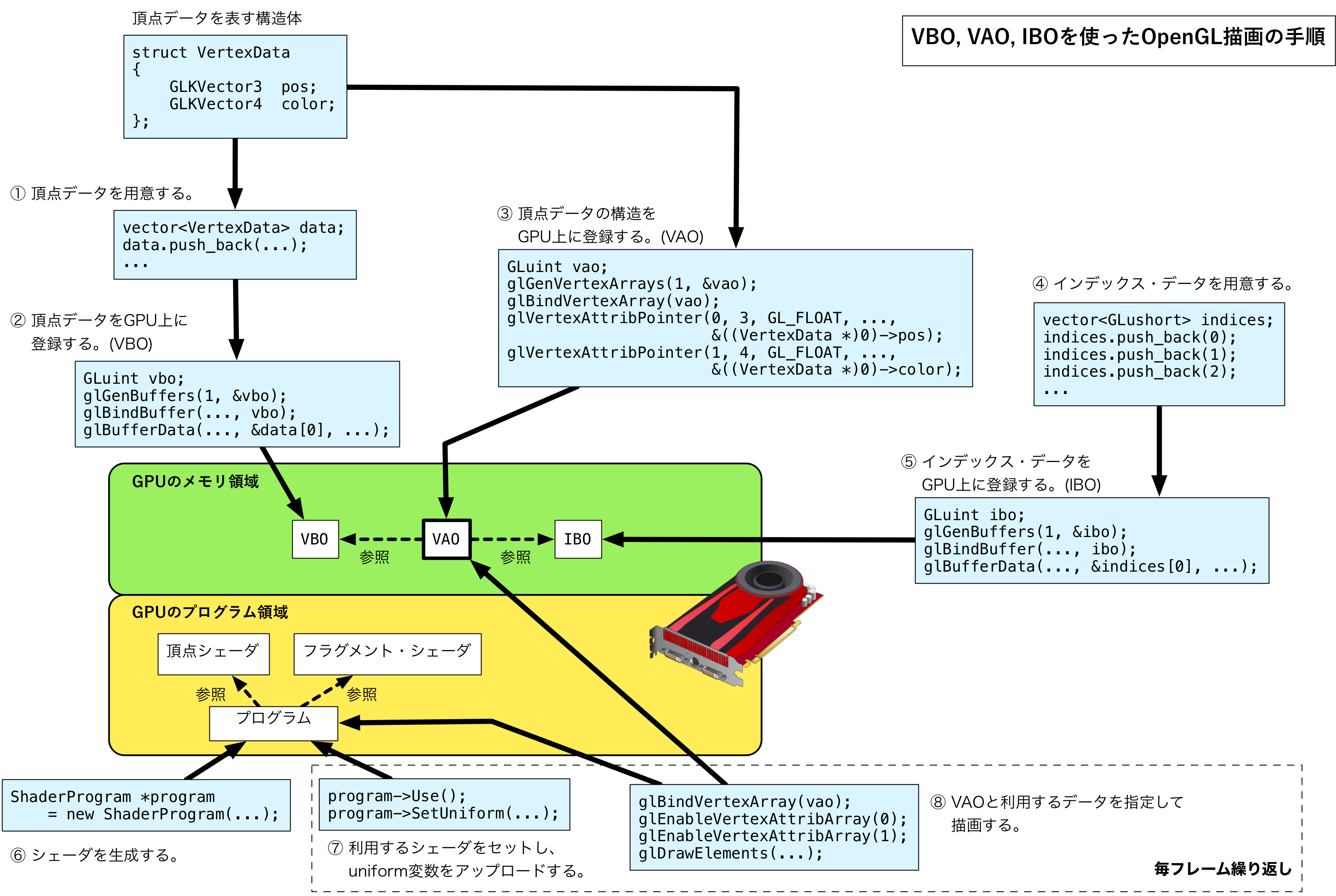
VBO, VAO, IBOを使って描画を行う手順についてまとめたものが次の図です。
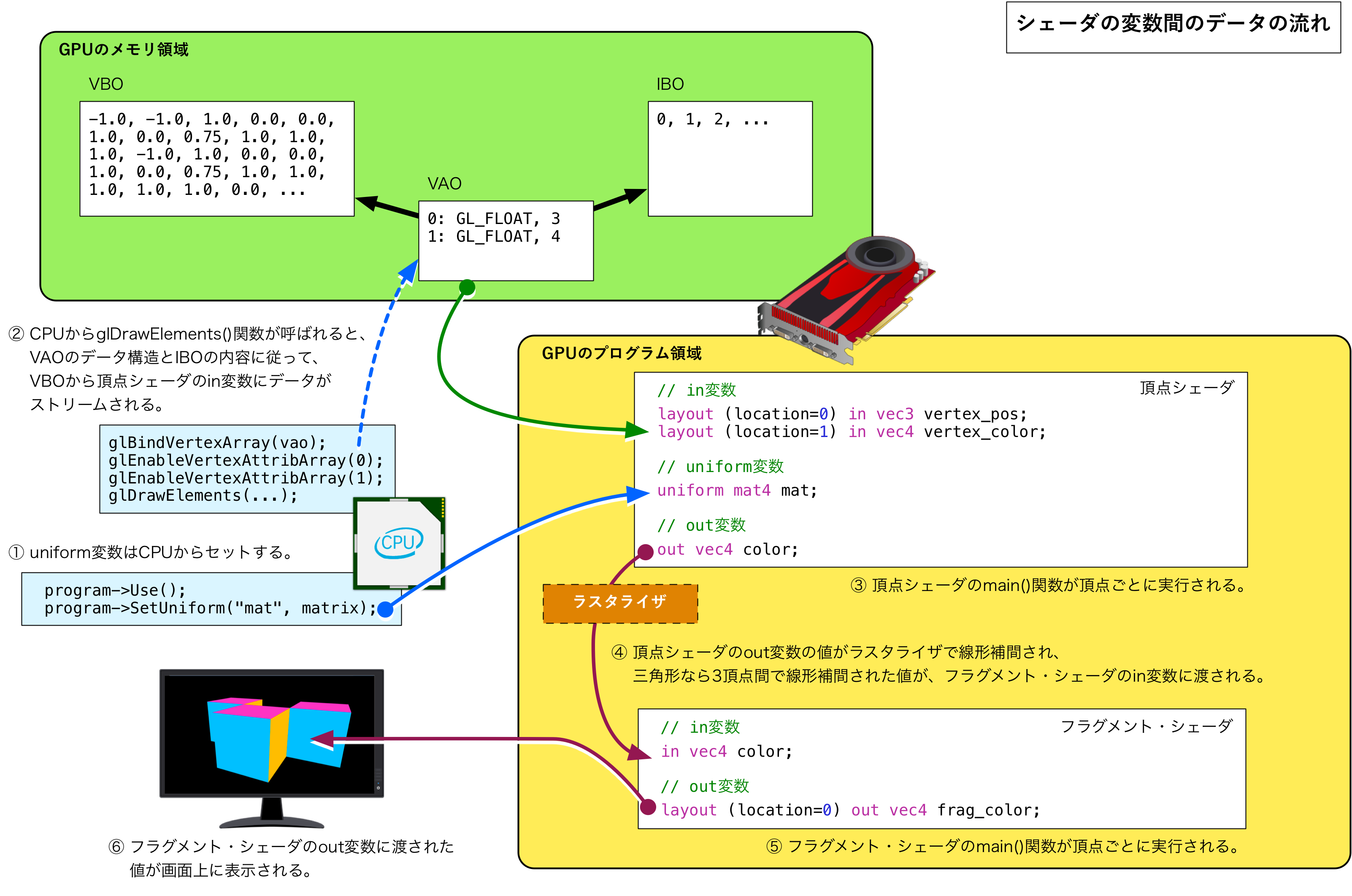
頂点シェーダとフラグメント・シェーダに、どのようにデータが入力され、どのようにデータが出力されるのかをまとめたのが、次の図になります。
この図を見ていただくと、毎フレームの画面の描画の手順は次のようになることが分かります。
- 利用するシェーダのプログラムをセットする (
program->Use()) - 必要なuniform変数をセットする (
program->SetUniform(...)) - 描画対象となる3DモデルのVAOをバインドする (
glBindVertexArray(vao)) - VBOからシェーダに流し込むデータの番号を明示する (
glEnableVertexAttribArray(...)) -
glDrawElements()関数を呼び出す。
それでは、これらの手順が復習できたところで、2節からは、ライティングに必要なコードを書いていきましょう。
2. ライティングに必要な法線データの追加
ライティングを考えないこれまでの描画では、頂点データは、位置情報(3次元ベクトル)と色(4次元ベクトル)の2つのデータだけで表されていました。
それに対して、**ライティングを行う場合には、各頂点ごとに、法線ベクトルというデータが必要になります。**法線ベクトルは、頂点を結んでできるポリゴンの面が、どの方向を向いているかを表すベクトルです。
さて、法線ベクトルは、なぜ必要なのでしょうか? 頂点を結んでできるポリゴンの面がどちらを向くかなど、自明のことではないでしょうか?(実際、2個の3次元ベクトルの外積を計算するだけで面の向きは計算できます)
なぜ法線ベクトルが必要かと言えば、ポリゴンの頂点データは1個ずつ頂点シェーダに渡されて処理されるのであって、ポリゴン(面)単位で処理されるわけではないためです。これはフラグメント・シェーダでも同じことで、フラグメントが表す1ピクセルごとのデータが渡されるだけで、ポリゴン(面)単位では処理されません。そのため、各頂点ごとに、その頂点を使って作る面がどちらの方向を向いているかというデータを持っておかなければ、ライトが当たった面の色は計算できないのです。
ちなみに、このような理由で法線ベクトルを用意しますので、(0, 0, 0)の位置にある頂点データであっても、(1, 0, 0)の方向を向いている頂点データと、(0, 1, 0)の方向を向いている頂点データは別々に用意しなければいけません。
それでは、法線ベクトル (normal vector) を表す normal 変数を、頂点データを表す VertexData 構造体に追加しましょう。
struct VertexData
{
GLKVector3 pos;
GLKVector3 normal;
GLKVector4 color;
};
Gameクラスのコンストラクタで、頂点データを登録するコードを次のように書き換え、立方体のデータを用意しましょう。位置座標、法線ベクトル、色の順番にデータを書き並べました。
Game::Game()
{
// 省略
// 手前の面
data.push_back({ { -1.0f, -1.0f, 1.0f }, { 0.0f, 0.0f, 1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, 1.0f }, { 0.0f, 0.0f, 1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 1.0f }, { 0.0f, 0.0f, 1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 1.0f }, { 0.0f, 0.0f, 1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { -1.0f, 1.0f, 1.0f }, { 0.0f, 0.0f, 1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { -1.0f, -1.0f, 1.0f }, { 0.0f, 0.0f, 1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
// 奥の面
data.push_back({ { -1.0f, -1.0f, -1.0f }, { 0.0f, 0.0f, -1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, -1.0f }, { 0.0f, 0.0f, -1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, -1.0f }, { 0.0f, 0.0f, -1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, -1.0f }, { 0.0f, 0.0f, -1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { -1.0f, 1.0f, -1.0f }, { 0.0f, 0.0f, -1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { -1.0f, -1.0f, -1.0f }, { 0.0f, 0.0f, -1.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
// 上の面
data.push_back({ { -1.0f, 1.0f, -1.0f }, { 0.0f, 1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, -1.0f }, { 0.0f, 1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 1.0f }, { 0.0f, 1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 1.0f }, { 0.0f, 1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { -1.0f, 1.0f, 1.0f }, { 0.0f, 1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { -1.0f, 1.0f, -1.0f }, { 0.0f, 1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
// 下の面
data.push_back({ { -1.0f, -1.0f, -1.0f }, { 0.0f, -1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, -1.0f }, { 0.0f, -1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, 1.0f }, { 0.0f, -1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, 1.0f }, { 0.0f, -1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { -1.0f, -1.0f, 1.0f }, { 0.0f, -1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
data.push_back({ { -1.0f, -1.0f, -1.0f }, { 0.0f, -1.0f, 0.0f }, { 1.0f, 0.0f, 0.75f, 1.0f } });
// 左の面
data.push_back({ { -1.0f, -1.0f, -1.0f }, { -1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { -1.0f, -1.0f, 1.0f }, { -1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { -1.0f, 1.0f, 1.0f }, { -1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { -1.0f, 1.0f, 1.0f }, { -1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { -1.0f, 1.0f, -1.0f }, { -1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { -1.0f, -1.0f, -1.0f }, { -1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
// 右の面
data.push_back({ { 1.0f, -1.0f, -1.0f }, { 1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, 1.0f }, { 1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 1.0f }, { 1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, 1.0f }, { 1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { 1.0f, 1.0f, -1.0f }, { 1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
data.push_back({ { 1.0f, -1.0f, -1.0f }, { 1.0f, 0.0f, 0.0f }, { 1.0f, 0.75f, 0.0f, 1.0f } });
// 以下、続く
}
この頂点データに対応したインデックス・データは、これまでと同様、for文で単純に登録するだけで良いでしょう。
std::vector<GLushort> indices;
for (int i = 0; i < data.size(); i++) {
indices.push_back(i);
}
VBO, VAO, IBOを生成し、データを登録するコードは、次のようになります。VBOとIBOの生成する方法はこれまでと同じですが、VAOで登録するデータに、GL_FLOAT型のデータ3個分の法線ベクトルのデータが増えていることに注意してください。
glGenBuffers(1, &vbo);
glBindBuffer(GL_ARRAY_BUFFER, vbo);
glBufferData(GL_ARRAY_BUFFER, sizeof(VertexData) * data.size(), &data[0], GL_STATIC_DRAW);
glGenVertexArrays(1, &vao);
glBindVertexArray(vao);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, sizeof(VertexData), &((VertexData *)0)->pos);
glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, sizeof(VertexData), &((VertexData *)0)->normal);
glVertexAttribPointer(2, 4, GL_FLOAT, GL_FALSE, sizeof(VertexData), &((VertexData *)0)->color);
glGenBuffers(1, &indexBuffer);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, indexBuffer);
glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(GLushort) * indices.size(), &indices[0], GL_STATIC_DRAW);
3. 頂点シェーダを書き換える
次に、ライティングをサポートするように、頂点シェーダを書き換えます。
頂点データに法線ベクトルが増えましたので、次のように、法線ベクトルのデータを受け取るための vertex_normal 変数を in 変数として追加します。
layout (location=0) in vec3 vertex_pos;
layout (location=1) in vec3 vertex_normal;
layout (location=2) in vec4 vertex_color;
ライトの向きを表すベクトルが必要となりますので、vec3 型の light_dir 変数を uniform 変数として追加します。またライトの向きを正しく計算するためには、プロジェクション行列やビュー行列と掛け合わされていない、単体のモデル行列が必要となりますので、この行列を受け取るための uniform 変数を、model_mat 変数という名前で追加します。これまで mat 変数という名前で用意していたプロジェクション行列・ビュー行列・モデル行列を掛け合わせた行列を受け取るための変数は、区別しやすいように、pvm_mat 変数という名前にリネームしておきましょう。
uniform vec3 light_dir;
uniform mat4 pvm_mat;
uniform mat4 model_mat;
最後に、追加したこれらの変数を使って、ライティングの計算を行うための頂点シェーダの実装を次のように書き換えます。詳しい解説は6節でします。
void main()
{
gl_Position = vec4(vertex_pos, 1.0) * pvm_mat;
vec3 normal = normalize((vec4(vertex_normal, 0.0) * model_mat).xyz);
float power = dot(normal, -normalize(light_dir));
power = clamp(power, 0.0, 1.0);
color = vertex_color * power;
}
なお今回の記事では、ライティングの計算は頂点シェーダのみで行いますので、フラグメント・シェーダは書き換える必要はありません。これまで通り、次のようなコードとなります。
# version 410
in vec4 color;
layout (location=0) out vec4 frag_color;
void main()
{
frag_color = color;
}
4. 描画のコードを書き換える
Render()関数の実装を書き換えて、シェーダにライトの向きを渡すようにしましょう。ここでは、正面から見て、右下奥方向にライトが向くように、(1, -1, -2)のベクトルを渡しています。奥行方向の値が大きいので、Z方向に強くライトが当たる計算です。
void Game::Render()
{
// 前半省略
program->Use();
GLKVector3 lightDir = GLKVector3Make(1.0f, -1.0f, -2.0f);
program->SetUniform("light_dir", lightDir);
// 以下、続く
}
VAOをバインドしている箇所を書き換えて、頂点データとして使用するデータが、0番の位置座標、1番の法線ベクトル、2番の色情報であることを明示します。ここを書き換えるのを忘れると、せっかく追加した法線ベクトルが正しく渡されなくなって、ライティングの計算が正常に行えなくなってしまいます。
glBindVertexArray(vao);
glEnableVertexAttribArray(0);
glEnableVertexAttribArray(1);
glEnableVertexAttribArray(2);
最後に、単体のモデル行列と、プロジェクション行列・ビュー行列・モデル行列を掛け合わせた行列を、uniform変数の model_mat 変数と pvm_mat 変数にセットします。そして glDrawElements()関数を呼び出して描画を実行します。
GLKMatrix4 modelMat = GLKMatrix4Identity;
program->SetUniform("model_mat", modelMat);
GLKMatrix4 pvmMat = GLKMatrix4Multiply(projViewMat, modelMat);
program->SetUniform("pvm_mat", pvmMat);
glDrawElements(GL_TRIANGLES, (GLsizei)data.size(), GL_UNSIGNED_SHORT, (void *)0);
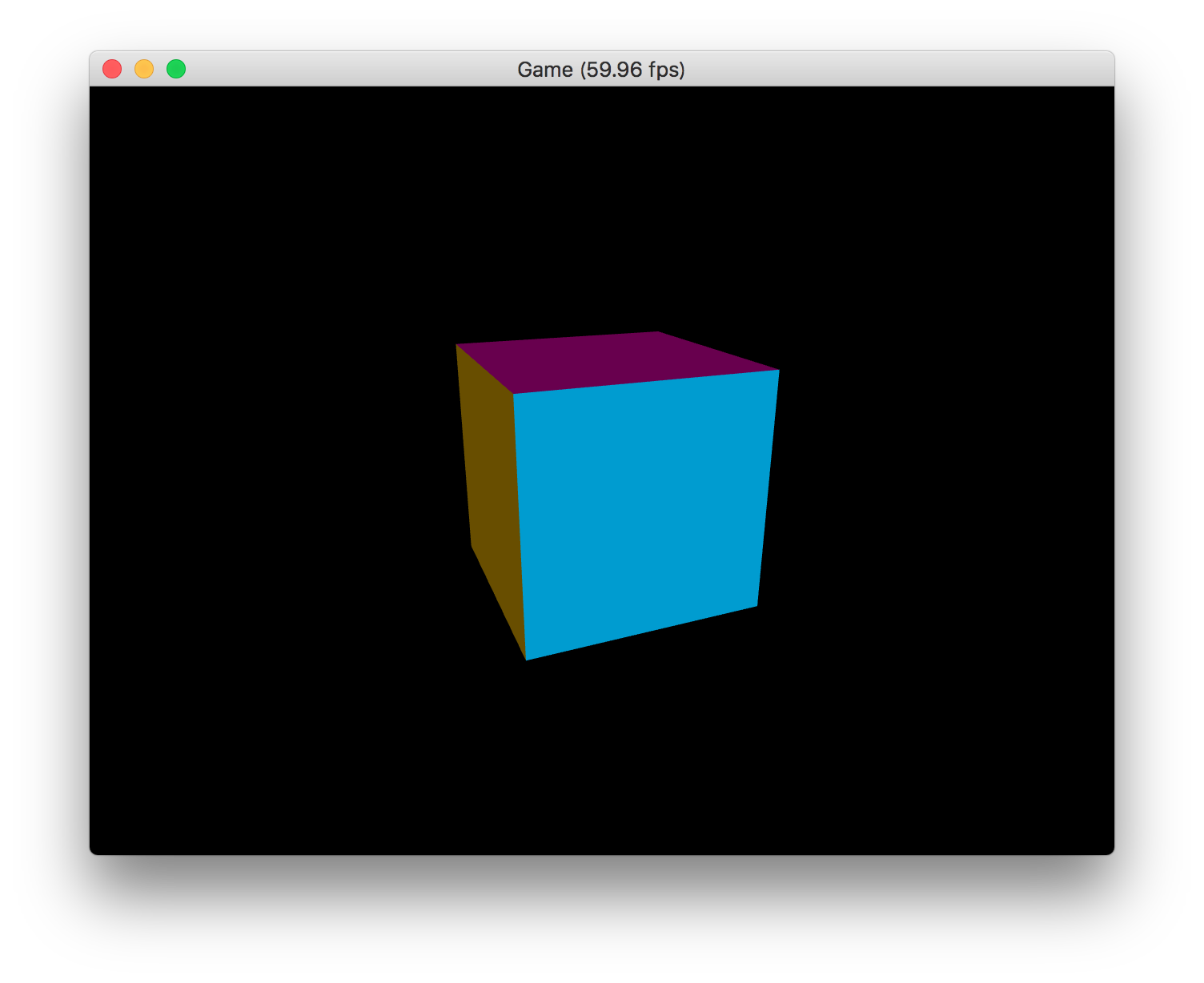
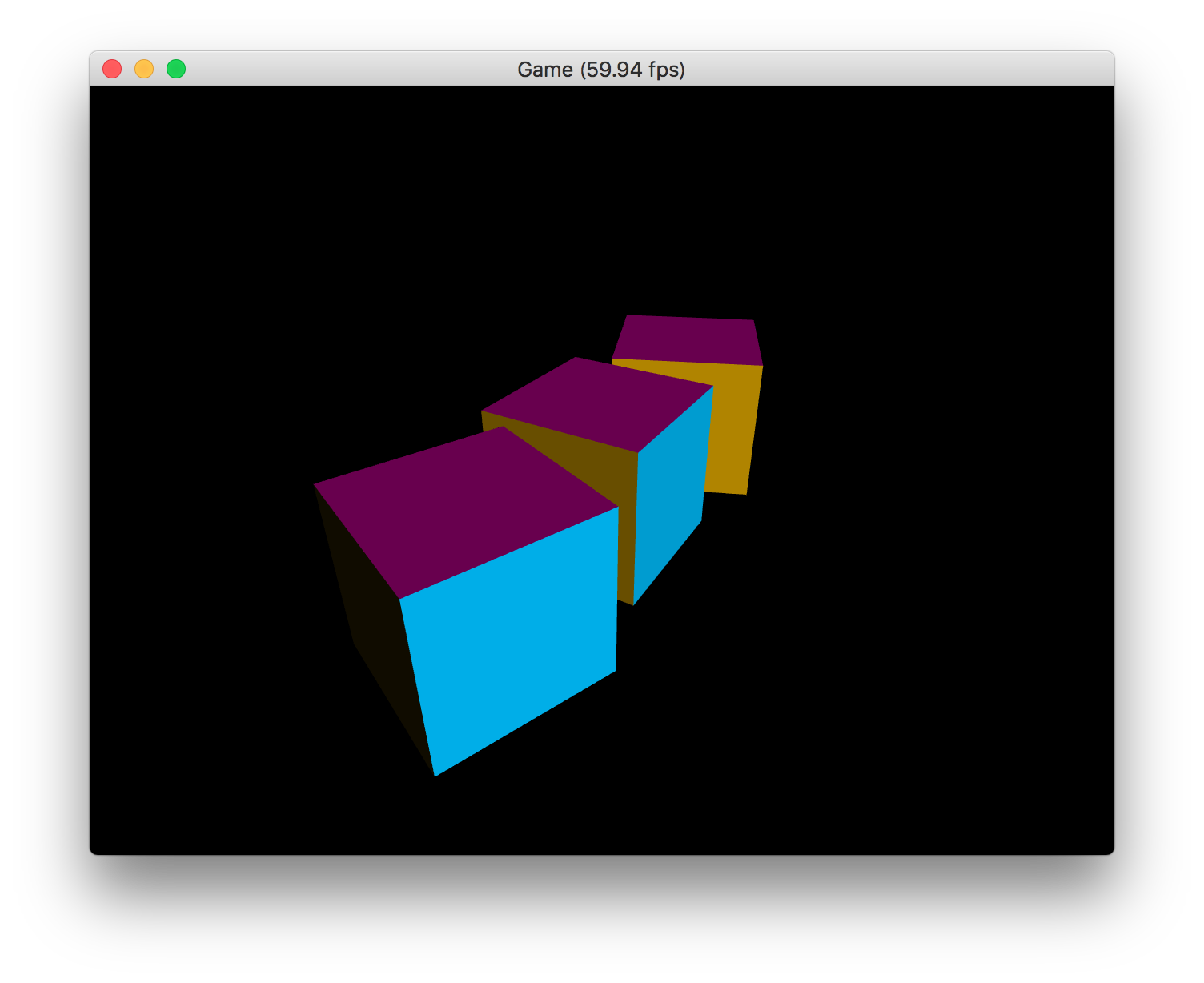
実行結果は、次のようになります。Z方向に強くライトが当たるようにしていたので、手前の水色の面が、上や左の面よりも明るく描画されているのが分かります。
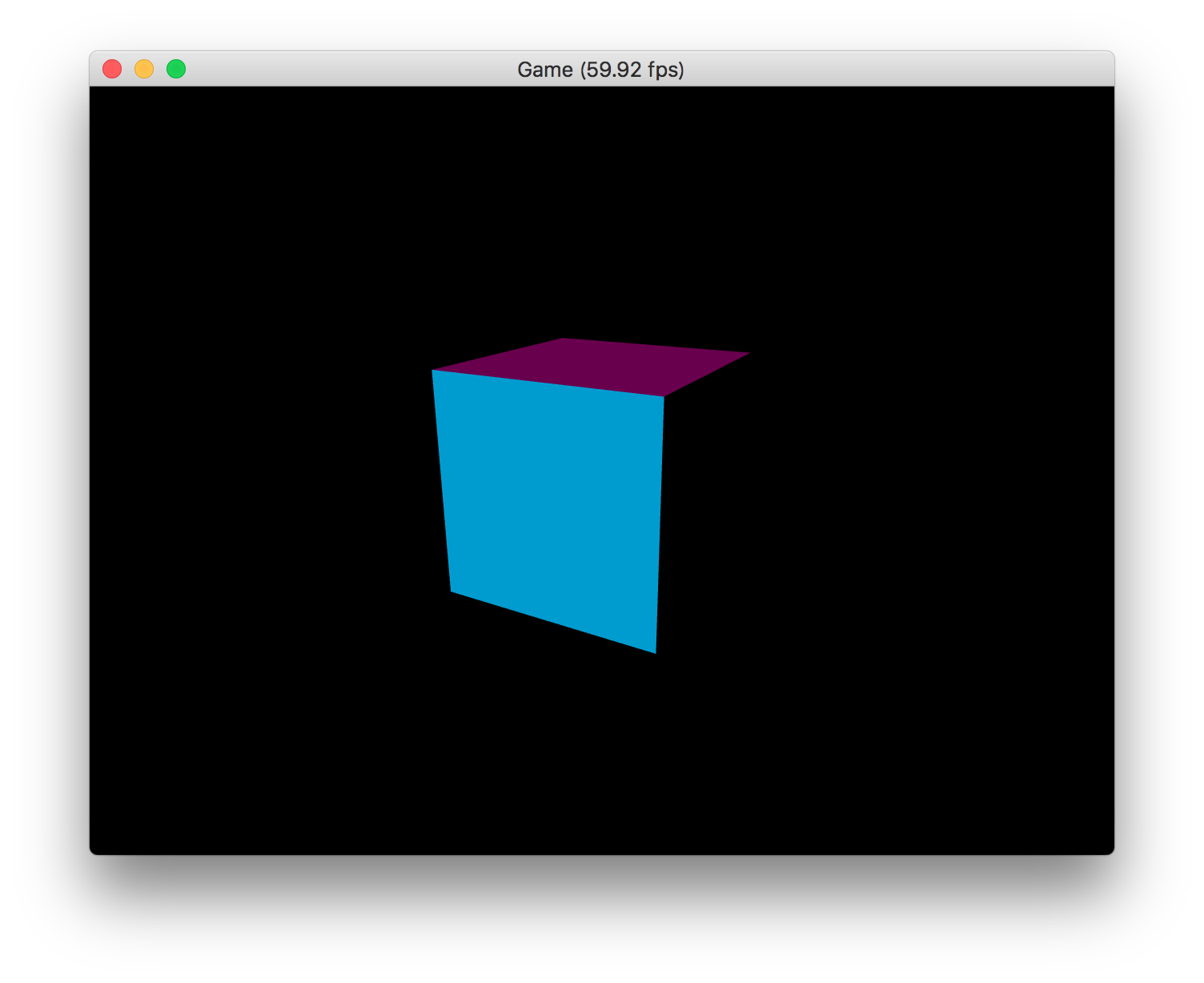
右から見ると、ライトが右下奥方向を向いているので、右の面にはライトが当たらず、真っ黒になっているのが分かります。
ここまでのプロジェクト:MyGLGame_step4-1a.zip
5. オブジェクトを増やしてみる
光の当たり方を確認するために、ボックスを少しずつ回転させて3つ並べて描画してみましょう。
GLKMatrix4 modelMat = GLKMatrix4Identity;
program->SetUniform("model_mat", modelMat);
GLKMatrix4 pvmMat = GLKMatrix4Multiply(projViewMat, modelMat);
program->SetUniform("pvm_mat", pvmMat);
glDrawElements(GL_TRIANGLES, (GLsizei)data.size(), GL_UNSIGNED_SHORT, (void *)0);
modelMat = GLKMatrix4Identity;
modelMat = GLKMatrix4Translate(modelMat, 2.5f, 0.0f, 0.0f);
modelMat = GLKMatrix4RotateY(modelMat, M_PI / 8);
program->SetUniform("model_mat", modelMat);
pvmMat = GLKMatrix4Multiply(projViewMat, modelMat);
program->SetUniform("pvm_mat", pvmMat);
glDrawElements(GL_TRIANGLES, (GLsizei)data.size(), GL_UNSIGNED_SHORT, (void *)0);
modelMat = GLKMatrix4Identity;
modelMat = GLKMatrix4Translate(modelMat, -2.5f, 0.0f, 0.0f);
modelMat = GLKMatrix4RotateY(modelMat, -M_PI / 8);
program->SetUniform("model_mat", modelMat);
pvmMat = GLKMatrix4Multiply(projViewMat, modelMat);
program->SetUniform("pvm_mat", pvmMat);
glDrawElements(GL_TRIANGLES, (GLsizei)data.size(), GL_UNSIGNED_SHORT, (void *)0);
これを実行してみると、次のようになります。左手前から右奥に向かって光が進んでいますので、反対側を向いている右端のボックスの青い面が少し暗くなっていることが分かります。それに対して、光のほぼ正面を向いているボックスの青い面はかなり明るいですね。
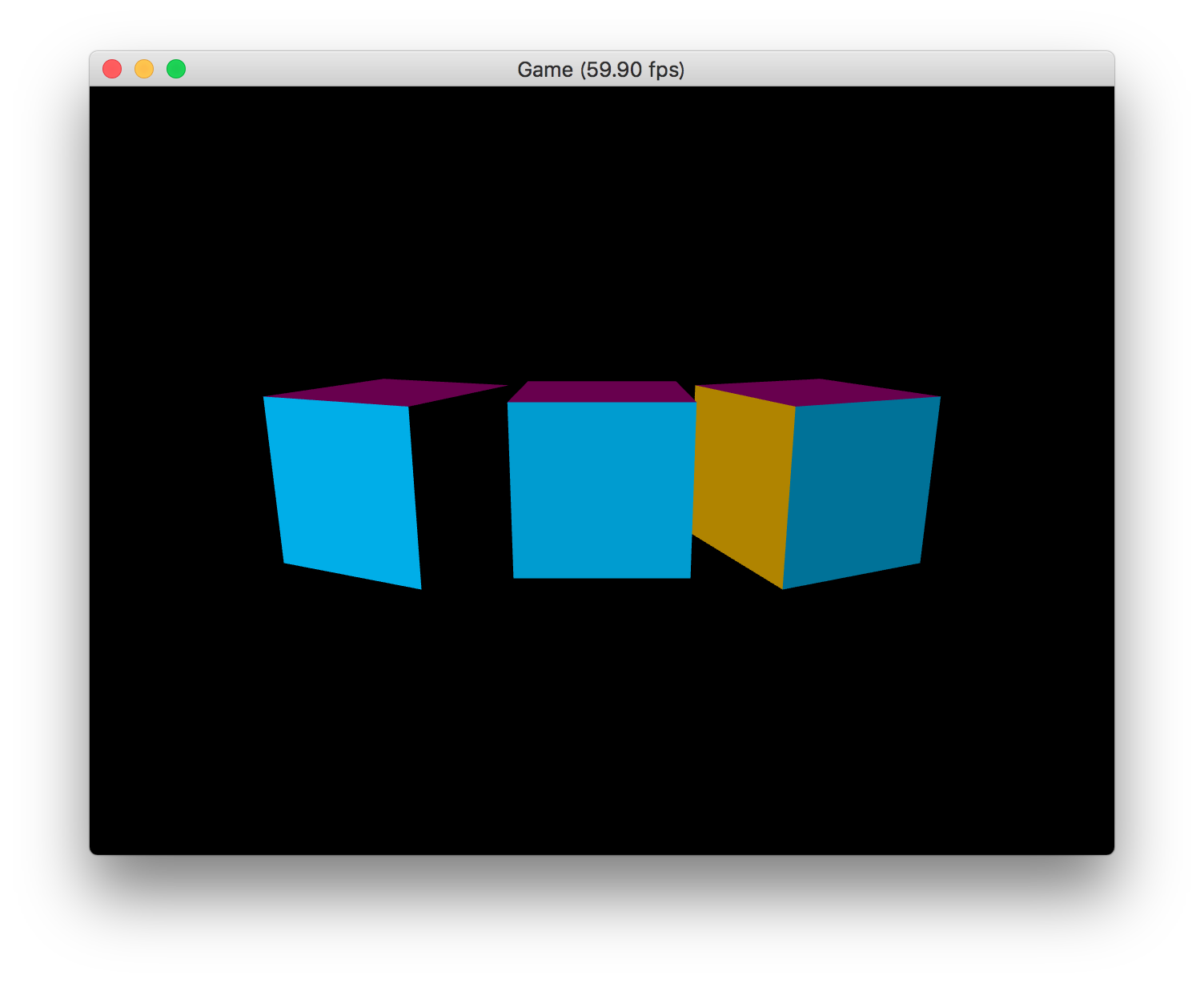
カメラを回転させて、左側から見てみましょう。すると、右端のボックスの黄色い面にはほぼ正面から光が当たっているためにかなり明るくなり、真ん中のボックスの黄色い面には斜めから光が当たるために少し暗くなり、左端のボックスは光がかなり横から当たるため、とても暗くなっていることが分かります。
ここまでのプロジェクト:MyGLGame_step4-1b.zip
6. 平行光源のライティング計算
それでは平行光源のライティングの原理について解説しましょう。
平行光源とは、光源から光がまっすぐに進み、その光が物体に当たって明暗をつける光源のことです。光が平行に進むということは、無限遠から来た光が物体に当たっているということです。無限遠から届いている光ですから、ここまで届いた以上、オブジェクトの周辺数メートルから数キロメートル程度の範囲では、平行光源の光は距離によって減衰することはありません。現実にはそのような光源は太陽くらいしかありませんので、太陽光をシミュレートするために使う場合が多いですが、十分に狭い部屋で天井から強いライトが当たっていると考える場合などに使用することもできるでしょう。
それでは、平行光源は物体にどのように明暗をつけるのでしょうか。
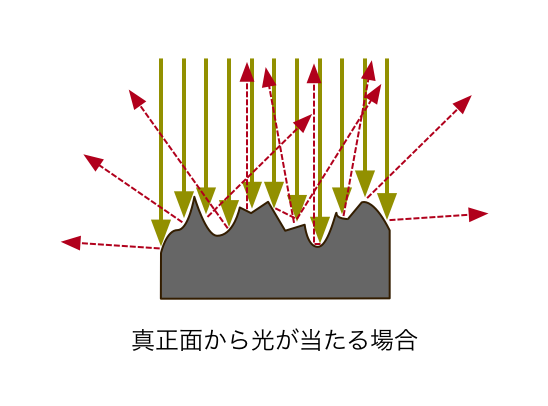
次の図を見てください。この図は、面に当たった光線がどのように跳ね返り、それによって面の色がどのように変わるかということを示しています。
ここで、**物体の表面は適度にざらついていて、物体表面にやってきた光子が、様々な方向に跳ね返る(乱反射する)**ということを前提にします。そのため、カメラや人間の目がどこにあるかということに関係なく、光の当たる角度次第で、どこから見ても一様に同じ明るさになると考えます。
この図が示す通り、物体の面に真正面から光が当たった場合には、その面は光の影響を強く受けて明るくなります。それに対して、光が斜めから当たった場合には、光の影響が弱くなり、少し暗くなります。光がさらに斜めから当たった場合には、ほとんど影響を受けることなく、真っ暗になります。
太陽から降り注ぐ無数の光子が、まっすぐに面に当たっている様子と、斜めから当たっている様子を想像してもらうと、面に当たる強さが異なり、それによって明るさも変わることが想像できるでしょう。ほら、ホースから勢いよく出た水が真正面から当たると痛いですが、斜めから当たってもそれほど痛くはないですよね? ミクロに考えると、光子が当たる角度が斜めになるほど単位面積あたりに当たる光子の数が減っていくので、だんだんと暗くなっていくのです。
この光の明暗をシミュレートするために、平行光源のライティングでは、内積(ドット積)の計算を行います。ドット積に馴染みがない方もいらっしゃるかも知れませんが、2つのベクトルのXの値同士、Yの値同士、Zの値同士を掛け合わせ、それをすべて足したものがドット積です。簡単です。
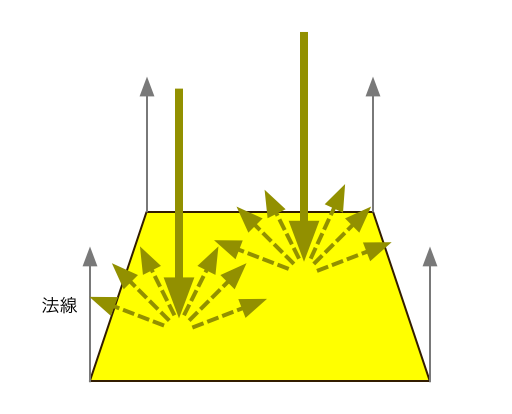
6-1. 正面から光が当たる場合
例として、面に対して真正面から光が当たっている場合を考えてみましょう。ここで、面の法線ベクトル N は (0, 1, 0)(したがって全ての頂点の法線ベクトルも (0, 1, 0) )、やって来る平行光源の方向ベクトル L は (0, -1, 0) とします。
ここで、平行光源の方向ベクトルを反対方向に向けるためにマイナス倍して、それと法線ベクトルとの内積(ドット積)を計算してみましょう。法線ベクトル N の要素を (nx, ny, nz)、光の方向ベクトル L の要素を (lx, ly, lz) とします。
\begin{align}
N\cdot (-L) &= nx \cdot (-lx) + ny \cdot (-ly) + nz \cdot (-lz)\\
&= 0 \cdot 0 + 1 \cdot 1 + 0 \cdot 0\\
&= 1
\end{align}
となり、ドット積は 1 になります。つまり、面の明るさは 1 です。
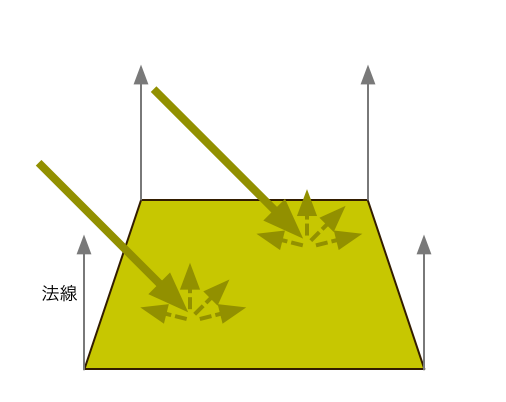
6-2. 斜めに光が当たる場合
次に、斜め45度から光が当たる場合を考えましょう。L = (0.71, -0.71, 0) とします。
法線ベクトルと光の逆方向ベクトルのドット積を計算しましょう。
\begin{align}
N\cdot (-L) &= nx \cdot (-lx) + ny \cdot (-ly) + nz \cdot (-lz)\\
&= 0 \cdot (-0.71) + 1 \cdot 0.71 + 0 \cdot 0\\
&= 0.71
\end{align}
となり、ドット積は 0.71 になります。つまり、面の明るさは 0.71 です。少し小さな値になりました。
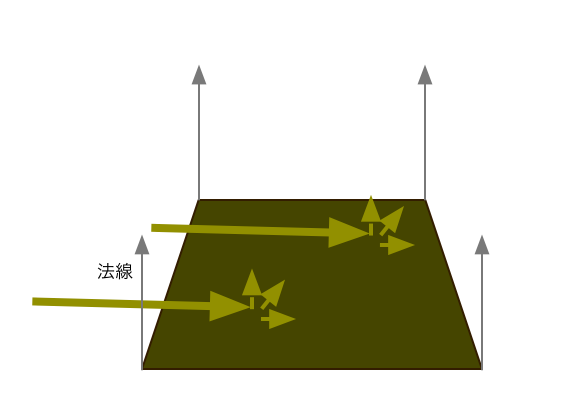
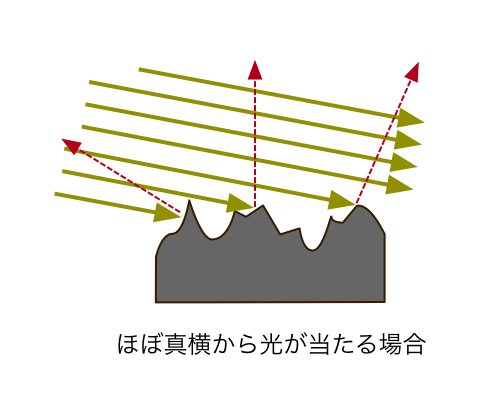
6-3. 真横から光が当たる場合
最後に、真横から光が当たる場合を考えましょう。L = (1, 0, 0) とします。(下の図は真横からではなく少し角度がついていますが、ゼロ度だと思って見てください)
法線ベクトルと光の逆方向ベクトルのドット積を計算しましょう。
\begin{align}
N\cdot (-L) &= nx \cdot (-lx) + ny \cdot (-ly) + nz \cdot (-lz)\\
&= 0 \cdot (-1) + 1 \cdot 0 + 0 \cdot 0\\
&= 0
\end{align}
となり、ドット積は 0 になります。つまり、面の明るさは 0 です。
このように、法線ベクトルと光の逆ベクトルの内積(ドット積)を計算することで、面の明るさを求めることができます。ドット積の値が 0 未満になった場合には、光が当たらなかったと考えて、値は 0 とします。
これはランバート反射と呼ばれる拡散反射モデルの実装になります(実際にはさらに光の色も考慮しなければいけませんので、この後のページで改良しましょう)。多くの物体について、これが物理的に正しいわけではありません。かなり大雑把に明暗の出方をシミュレートできるというだけなのですが、1回のドット積(すなわち掛け算3回と足し算2回)だけで計算できるので、よく使われる光の計算方法です。
6-4. 頂点シェーダの実装について
頂点シェーダの実装部分を再掲すると、次の通りです。
void main()
{
gl_Position = vec4(vertex_pos, 1.0) * pvm_mat;
vec3 normal = normalize((vec4(vertex_normal, 0.0) * model_mat).xyz);
float power = dot(normal, -normalize(light_dir));
power = clamp(power, 0.0, 1.0);
color = vertex_color * power;
}
最初の行の「gl_Position = vec4(vertex_pos, 1.0) * pvm_mat;」は、これまで通り、頂点の位置座標にプロジェクション行列・ビュー行列・モデル行列の変換行列を掛けて、座標変換を行うためのコードです。
次の「vec3 normal = (vec4(vertex_normal, 0.0) * model_mat).xyz;」は、モデル行列を使って、法線ベクトルにモデルの移動・回転・スケールの変換をかけています。モデルが回転しているのですから、その法線ベクトルも回転させなければいけません。
モデル行列は4x4行列ですから、法線ベクトルを掛け算する前に、4次元ベクトルに変換しておく必要があります。gl_Position を計算する時にも同様に4次元ベクトルへの変換を行っていますが、こちらは元のデータが位置座標なので、4番目の値に 1.0 を補っています。法線ベクトルは座標ではなくベクトルですので、4番目の値には 0.0 を補います。行列で変換を行った後は xyz の値だけを取り出し、正規化して、回転させた法線ベクトルを取り出します。
4番目の値
wに 1 を入れると平行移動が有効になり、0 を入れると平行移動が無効になります(詳しくは「ゲームつくろー! DirectX技術編 その55 そもそも「w」って何なのか?」を見てください)。ベクトルの場合、回転したりスケーリングしたりしても正規化すればその性質を保てるのですが、平行移動によってXとYとZの値がそれぞれ異なる変化量でずれてしまうと、その性質が保てなくなってしまいます。そこで4番目のwの値には 0 を入れて、平行移動が効かないようにしなければならないのです。
そして光の方向ベクトルの逆ベクトルを求めて、念のため正規化した後(「方向ベクトル」と言ってはいるものの1、正規化しない値を放り込めた方がライトの向きを調整しやすいですよね)、法線ベクトルのドット積を、「float power = dot(normal, -normalize(light_dir));」で計算します。dot() 関数もGLSLの組み込み関数です。
こうして求めた面の明るさが 0.0〜1.0 の範囲に収まるように、組み込み関数 clamp() を使って、「power = clamp(power, 0.0, 1.0);」としておきます。
最後に、power 変数で表される明るさの数値を頂点の色 vertex_color に掛け合わせれば、その頂点における色に明暗をつけることができます。
7. まとめ
この記事では、シェーダの使い方を復習してから、法線ベクトルの必要性について述べ、法線ベクトルと光の逆方向ベクトルのドット積を求めることによって、平行光源からの光の影響を考慮した明暗をポリゴンの面に付けられるということを解説しました。
今回の内容をざっとまとめると、次の通りです。
- 平行光源は超強力な光源であり、平行な光が無限遠に届く。減衰はない。
- ポリゴンを構成する各頂点ごとに計算されるため、頂点データとして法線ベクトルが必要である。
- 平行光源の逆方向ベクトルと頂点の法線ベクトルの内積(ドット積)を計算することで、各頂点の明るさが求められる。
- これはランバート反射と呼ばれる拡散反射のモデルである。多くの場合、物理的に正しい明暗の出方ではないが、計算の単純さに対して結果の質は良い。
この記事で解説した平行光源のライティングは本当に簡易的なライティング実装ですが、簡易であってもライティングが有効になると、複雑な3Dモデルを読み込んで描画するテストができるようになります。
-
「方向ベクトル」と言えば数学的には正規化されていることが期待されることが多いでしょう。 ↩