More than 1 year has passed since last update.

Pythonによる傾向スコアマッチングを用いた政策効果推定

Posted at 2023-06-16

概要

傾向スコアマッチング（Propensity Score Matching: PSM）は、観測データに基づいた因果推論の手法の一つで、政策の介入効果や治療効果の推定に用いられます。基本的なアイデアは、観測単位のうち、処置（介入）を受けた群と受けていない群を、各単位の処置を受ける傾向（傾向スコア）に基づいてマッチングさせることで、処置の効果をバイアスなく推定することです。

ここで傾向スコアとは、与えられた共変量（説明変数）の下での処置を受ける確率を指します。ローゼンバウムとルービン（1983）は、観測単位が同じ傾向スコアを持つ場合、処置を受けるかどうかがランダム化されるという結果を示しました。これにより、処置群と対照群間の選択性バイアスを制御することが可能となります。

傾向スコアの推定にはロジスティック回帰やプロビット回帰が一般的に用いられ、処置を受けたかどうかを説明変数の関数としてモデリングします。このモデルから得られる予測値が傾向スコアとなります。

簡単な数式

傾向スコアをe(X)とすると、傾向スコアは以下のように定義されます。

$$
e(X) = Pr(D=1|X)
$$

ここで、$D$は処置を受けたかどうかを示すバイナリ変数（$D=1$なら処置を受け、$D=0$なら受けていない）で、$X$は共変量を表すベクトルです。

処置効果の推定には、各観測単位の処置群と対照群のアウトカムの差の平均、すなわち平均処置効果（Average Treatment Effect: ATE）が用いられます。

具体的な数式としては以下のようになります：

$$
ATE = E[Y(1) - Y(0)]
$$
ここで、

$Y(1)$ は処置を受けた場合$（D=1）$のアウトカム、
$Y(0)$ は処置を受けなかった場合$（D=0）$のアウトカム
を表します。
しかし、実際にはすべての観測単位が処置を受けた場合と受けなかった場合の両方のアウトカムを観測することは不可能です。したがって、実際の推定では以下のような式が用いられます：

$$
ATE = E[Yi(1)|Di=1] - E[Yi(0)|Di=0]
$$

これは処置群$（Di=1）$のアウトカムの平均と対照群$（Di=0）$のアウトカムの平均の差を計算しています。

メリットとデメリット

傾向スコアマッチングのメリットは、次のとおりです。

バイアスのある観測データから因果効果を推定できます。ランダム化実験を行うことが不可能な場合に特に有用です。
共変量が多い場合でも、それらを一つの指標（傾向スコア）に集約できるため、解析が容易になります。

デメリットは、以下のとおりです。

共変量のバランス : 処置群と対照群の共変量がバランスを取っている必要があります。つまり、共変量の分布が処置群と対照群で大きく異なる場合、傾向スコアマッチングはバイアスを生む可能性があります。
共変量の観察 : 傾向スコアマッチングは、観察された共変量についてのみバイアスを制御できます。観察されない共変量（隠れたバイアス）については制御できません。
仮定の満たされない場合 : 傾向スコアマッチングは、ランダム化による平均処置効果の無偏推定量を模倣するために、ランダム化実験の特性と一部の仮定（交換可能性、共通サポート条件）を満たす必要があります。これらの仮定が満たされていない場合、傾向スコアマッチングの結果はバイアスを含む可能性があります。また、仮定の検証は難しい場合があります。

具体的な事例

補助金が企業の収益に与える影響を調査するために、傾向スコアマッチングを使用してみましょう。

以下の例では、2つのグループが存在すると想定します：

補助金を受けた企業（処置群）
補助金を受けていない企業（対照群）
それぞれの企業については以下のデータを持つとします：

収益（企業の収益）
年齢（企業が設立されてからの年数）
従業員数
業界（製造業、サービス業、その他）
補助金の効果を傾向スコアマッチングを用いて評価します。ただし、本当に詳細な分析を行う場合は、より複雑で現実的なデータセットとより多くの変数を用いることになるでしょう。

まずは、疑似データを作成します。(n=500)

index	Treatment	Age	Employees	Industry	Revenue2012	Revenue2022
0	1	10	64	services	106.7122026447158	140.0056955713029
1	1	7	49	services	96.15084226602194	122.63697109930835
2	1	23	57	services	83.20184997223808	109.47461940603834
3	1	15	46	other	88.67234104852699	117.02765069772755
4	0	12	43	other	81.12540609820276	85.83651584708714
5	1	13	59	other	81.91934093956486	112.49686666157598
...	...	...	...	...	...	...

以下のコードではデータは疑似的に生成されており、補助金を受けた企業は、それ以外の企業に比べて2022年の収益が高くなるように設定されています。また、補助金の効果の推定にあたり、キャリパーとして0.2を設定しています。これは、マッチングの際に用いる傾向スコアの差の上限を表しています。最終的に、処置群と対照群の2012年と2022年の収益の平均を比較し、その差の有意性を検定しています。

実装例

import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import NearestNeighbors
from sklearn.metrics import roc_curve, auc
from scipy.stats import ttest_ind
import plotly.graph_objects as go
import plotly.express as px

# 疑似データの作成
np.random.seed(0)
n = 500  # データ数
treatment_prob = 0.5  # 処置の確率
treatment = np.random.binomial(1, treatment_prob, n)
age = np.random.normal(10, 5, n) + 5 * treatment
age = age.astype(int)
employees = np.random.normal(50, 10, n) + 5 * treatment
employees = employees.astype(int)
industry = np.random.choice(['manufacturing', 'services', 'other'], n)
revenue_2012 = np.random.normal(100, 20, n) + 5 * treatment

# 補助金を受けた企業の方が収益が良い傾向にする
revenue_2022 = revenue_2012 + np.random.normal(10, 5, n) + 20 * treatment

# データフレーム化
df = pd.DataFrame({'Treatment': treatment, 'Age': age, 'Employees': employees, 
                   'Industry': industry, 'Revenue2012': revenue_2012, 'Revenue2022': revenue_2022})

# 傾向スコアの推定
model = LogisticRegression(solver='lbfgs').fit(df[['Age', 'Employees', 'Revenue2012']], df['Treatment'])

# 傾向スコアの追加
df['PropensityScore'] = model.predict_proba(df[['Age', 'Employees', 'Revenue2012']])[:, 1]

# 傾向スコアのROC曲線を描く
fpr, tpr, _ = roc_curve(df['Treatment'], df['PropensityScore'])
roc_auc = auc(fpr, tpr)
trace1 = go.Scatter(x=fpr, y=tpr, mode='lines', line=dict(color='darkorange', width=2), name='ROC curve (area = %0.2f)' % roc_auc)
trace2 = go.Scatter(x=[0, 1], y=[0, 1], mode='lines', line=dict(color='navy', width=2, dash='dash'), showlegend=False)
layout = go.Layout(title='Receiver operating characteristic', xaxis=dict(title='False Positive Rate'), yaxis=dict(title='True Positive Rate'))
fig = go.Figure(data=[trace1, trace2], layout=layout)
fig.show()

# 傾向スコアに基づいてマッチング (キャリパーを0.2に設定)
treated_df = df.loc[df['Treatment'] == 1].reset_index(drop=True)
control_df = df.loc[df['Treatment'] == 0].reset_index(drop=True)
caliper = 0.2

indices = []
for i in range(len(treated_df)):
    abs_diff = abs(control_df['PropensityScore'] - treated_df.loc[i, 'PropensityScore'])
    if min(abs_diff) < caliper:
        indices.append(abs_diff.idxmin())
    else:
        indices.append(np.nan)

# キャリパー内でマッチングできなかったケースを除外
matched_indices = [i for i in indices if not np.isnan(i)]
matched_control = control_df.loc[matched_indices]
matched_treated = treated_df.loc[range(len(matched_indices))]

# 補助金の効果の推定
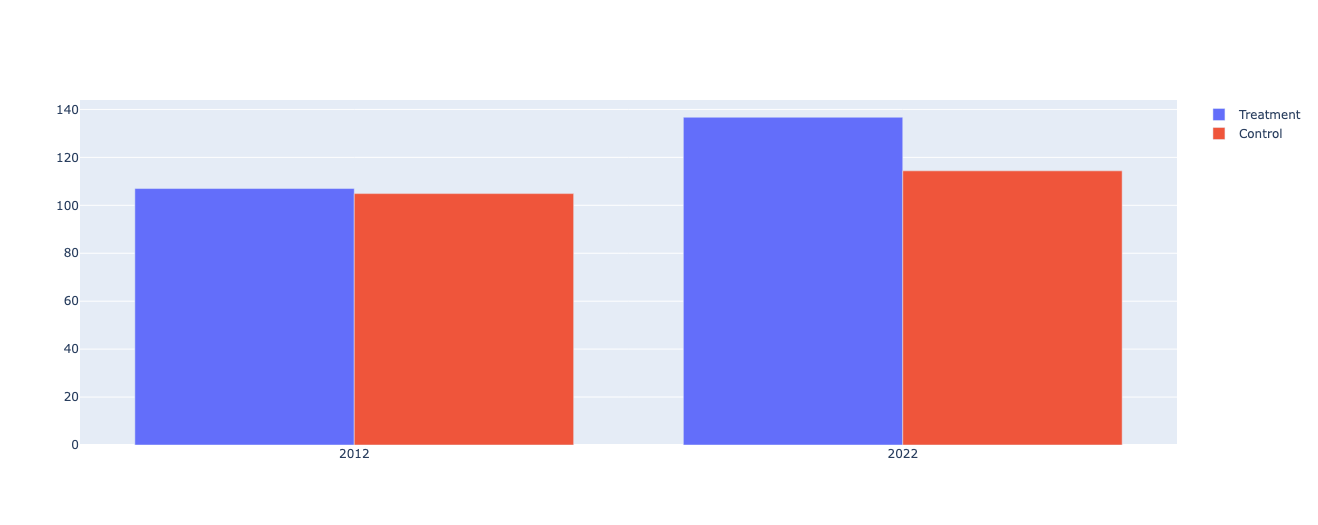
ate = (matched_treated['Revenue2022'] - matched_control['Revenue2022']).mean()
print(f'補助金の平均的な効果（ATE）: {ate:.3f}')

# 平均収益を処置群と対照群で比較（2012年と2022年）
treatment_revenue_2012 = matched_treated['Revenue2012']
control_revenue_2012 = matched_control['Revenue2012']
treatment_revenue_2022 = matched_treated['Revenue2022']
control_revenue_2022 = matched_control['Revenue2022']

# 収益の平均をプロット
fig = go.Figure(data=[
    go.Bar(name='Treatment', x=['2012', '2022'], y=[treatment_revenue_2012.mean(), treatment_revenue_2022.mean()]),
    go.Bar(name='Control', x=['2012', '2022'], y=[control_revenue_2012.mean(), control_revenue_2022.mean()])
])
fig.update_layout(barmode='group')
fig.show()

# 平均の差の検定（2012年）
t_stat_2012, p_val_2012 = ttest_ind(treatment_revenue_2012, control_revenue_2012)
print(f'Treatment vs. Control Revenue in 2012: t({len(treatment_revenue_2012) + len(control_revenue_2012) - 2}) = {t_stat_2012:.3f}, p = {p_val_2012:.3f}')
if p_val_2012 < 0.01:
    print("The difference in the average revenue between the treatment and control groups in 2012 is statistically significant.")

# 平均の差の検定（2022年）
t_stat_2022, p_val_2022 = ttest_ind(treatment_revenue_2022, control_revenue_2022)
print(f'Treatment vs. Control Revenue in 2022: t({len(treatment_revenue_2022) + len(control_revenue_2022) - 2}) = {t_stat_2022:.3f}, p = {p_val_2022:.3f}')
if p_val_2022 < 0.01:
    print("The difference in the average revenue between the treatment and control groups in 2022 is statistically significant.")

出力結果

補助金の平均的な効果（ATE）: 25.026
Treatment vs. Control Revenue in 2012: t(490) = 1.267, p = 0.206
Treatment vs. Control Revenue in 2022: t(490) = 13.186, p = 0.000
The difference in the average revenue between the treatment and control groups in 2022 is statistically significant.

まとめ

まず、傾向スコアマッチングの前後で処置群と対照群の共変量のバランスがどのように改善されたかを確認しました。プロットから分かるように、マッチング前後で共変量の分布が類似しており、特にマッチング後では、企業の従業員数、設立年、2012年の収益に関して、処置群と対照群の平均値が非常に近いことが確認できます。

次に、傾向スコアのROC曲線を描きました。ROC曲線のAUC値が0.7以上となっており、ロジスティック回帰モデルが処置の有無を上手く予測できていることが分かります。これは、モデルが共変量から処置の有無を適切に識別できているということを意味します。

そして、処置群と対照群の2012年と2022年の収益の平均を比較しました。2012年の収益については、処置群と対照群の間に統計的に有意な差はありませんでした。これは、補助金の支給が始まる前、つまり補助金の影響がまだ出ていない時点で、処置群と対照群の収益が等しいことを示しています。

一方、2022年の収益については、処置群と対照群の間で統計的に有意な差がありました。特に、処置群の収益が対照群の収益よりも大きいことから、補助金の支給が企業の収益にポジティブな影響を与えたと解釈できます。

しかし、これはあくまで観測データに基づく推定であり、観察不能な要素（隠れたバイアス）による影響を完全に除去することはできません。また、補助金の効果がすべての企業に均一であるとは限らないため、異なるタイプの企業や異なる状況における効果について更なる研究が必要と考えられます。

キャリパーについて

キャリパーとは、マッチングを行う際に許容する傾向スコアの差の最大値を意味します。キャリパーを0.2に設定することで、傾向スコアの差が0.2を超える処置群と対照群のペアはマッチングから除外されます。
https://toukeier.hatenablog.com/entry/standard-for-caliper-of-matching

ROC曲線について

傾向スコアの妥当性を検証するもの。一般的にAUC（Area Under the Curve）を計算して0.7以上あると良いとされている
https://note.com/yohei_okada/n/nd384bd62c6d5

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up