概要
mediba Advent Calendar 2022の13日目です。
この記事では国税庁が公開している酒税の数量データで主成分分析を行い、都道府県ごとのお酒の消費状況の特徴を把握してみます。
主成分分析とは
主成分分析(Principal Component Analysis)は次元圧縮・変数削減など情報集約を目的に使われます。
手順としては相関行列・相関行列の固有値・固有ベクトルを求め、各個体の第1・第2主成分得点を計算・プロット という流れになり、Rにおいてはprcomp()およびbiplot()にて主成分分析とプロットでの可視化をすることができます。
データソース
今回は以下の2つの統計データを利用します。
1) 酒類 販売統計
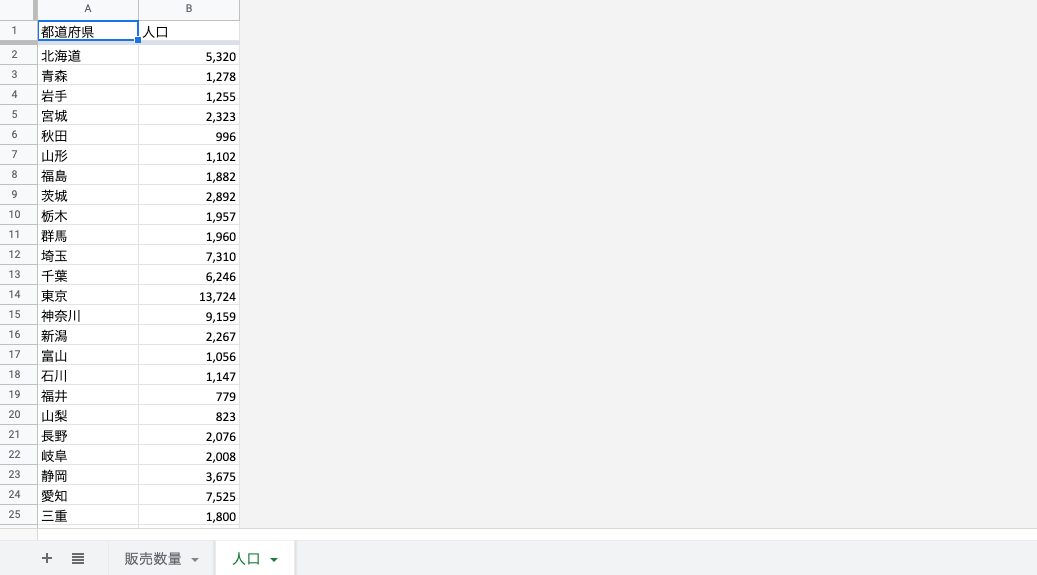
国税庁の令和2年度の間接税のデータから、都道府県ごとの酒類の販売(消費)数量を抽出します。今回は以下ページで公開されている「製成数量」のエクセルの「4(3)都道府県別の販売(消費)数量」のシートを利用します。
2) 人口統計
販売統計を人口あたりの数値に変換するため、総務省統計局の人口統計を利用します。
データソースの整形
元のエクセルは不要なセルが含まれておりそのままでは扱いづらいので、Googleスプレッドシート上で分析に適した形に整形します。
1) 酒類 販売統計
2) 人口統計
前処理
ライブラリの読み込み
tidyverseとgooglesheet4を読み込み、プロット時の文字化けを防ぐためpar()でグラフィックスパラメータのフォント指定をしておきます。
library(tidyverse)
library(googlesheets4)
par(family = "HiraKakuProN-W3")
データの読み込み
googlesheet4ライブラリのread_sheet()を利用して、スプレッドシートのデータをtibbleデータフレームとして読み込みます。ssパラメータではシートID、rangeパラメータではシート名を指定します。
df_sales <- read_sheet(
ss = "SPREADSHEET_ID",
range = "販売数量"
)
df_population <- read_sheet(
ss = "SPREADSHEET_ID",
range = "人口"
)
この2つのデータフレームは「都道府県」のカラムをキーとしてJOINさせます。
df_merged <-
left_join(df_sake, df_population, by = "都道府県")
df_merged
## # A tibble: 47 × 16
## 都道府県 清酒 合成清酒 連続式蒸留焼酎 単式蒸留焼酎 みりん ビール 果実酒
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 北海道 17379 943 28783 5259 3540 88577 14736
## 2 青森 5440 430 6271 3142 474 18966 2690
## 3 岩手 5499 271 4588 3573 527 18833 2723
## 4 宮城 9495 448 6092 7130 1657 33130 6244
## 5 秋田 5942 373 5005 2133 416 15557 1925
## 6 山形 5808 359 5168 2142 786 15417 2469
## 7 福島 9611 371 4232 6997 1149 27043 3491
## 8 茨城 9650 485 7074 7931 1283 33434 6068
## 9 栃木 6783 273 6048 4638 847 22771 3539
## 10 群馬 6211 246 8065 3537 1124 21494 3765
## # … with 37 more rows, and 8 more variables: 甘味果実酒 <dbl>,
## # ウイスキー <dbl>, ブランデー <dbl>, 発泡酒 <dbl>,
## # `原料用アルコール・スピリッツ` <dbl>, リキュール <dbl>, その他 <dbl>,
## # 人口 <dbl>
都道府県を1レコードとして各酒類の販売数量および人口のカラムを持ったデータフレームとなりました。
データの整形
データフレームを主成分分析(prcomp)に適した形に整形します。
df_pca <- df_merged %>%
mutate_if(.predicate = is.numeric, .funs = ~ . / 人口) %>%
select(-その他, -みりん, -人口) %>% ## 不要なカラムの除去
column_to_rownames(var = "都道府県")
mutate_if()では第一引数に条件としての叙述関数(predicate)、第二引数に実行したい関数を渡すことで「任意の条件に当てはまるカラムに関数を適用」することができます。
ここではチルダから始まるラムダ式を利用して、numeric型のカラムに対して人口での割り算を適用しています。(人口あたりの指標に変換しています)
またこの後の主成分分析で「行名(rownames)」が必要となるため、column_to_rownames()で任意のカラム(都道府県)の行名変換を行なっています。
主成分分析
それではデータフレームをprcomp()に渡して主成分分析を実行してみます。
df_pca %>%
prcomp(scale = T)
ここではscaleパラメータにTを指定し、標準化した値(単位を揃えた値)で計算しています。
※標準化:各値を平均で引いて標準偏差で割ること(↓)
z_i = \frac{x_i-\bar{x}}{sdx}
累積寄与率の確認
今回の分析結果の精度を確認してみます。
df_pca %>%
summary()
## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 1.9933 1.5056 1.2497 1.05235 0.92764 0.82102 0.66080
## Proportion of Variance 0.3311 0.1889 0.1301 0.09229 0.07171 0.05617 0.03639
## Cumulative Proportion 0.3311 0.5200 0.6502 0.74245 0.81416 0.87033 0.90672
## PC8 PC9 PC10 PC11 PC12
## Standard deviation 0.59553 0.51532 0.46761 0.41901 0.32394
## Proportion of Variance 0.02955 0.02213 0.01822 0.01463 0.00874
## Cumulative Proportion 0.93627 0.95840 0.97662 0.99126 1.00000
Standard deviationが標準偏差、Proportion of Varianceが寄与率、Cumulative Proportionが累積寄与率となります。
主成分分析では分散が最大の軸から順に主成分軸が決まるため、Standard deviationは分散の大きい順に並びます。
Proportion of Varianceは当該主成分が占める情報量の割合です。つまり第二主成分までで情報量の52%(PC1 + PC2 = 52%)が説明できる ということになります。
今回の場合、第二主成分までの累積寄与率では情報の損失が大きく、2軸だけでは解釈が難しいかもしません。
プロットと考察
主成分分析の結果をbiplotで可視化してみます。
df_pca %>%
biplot()
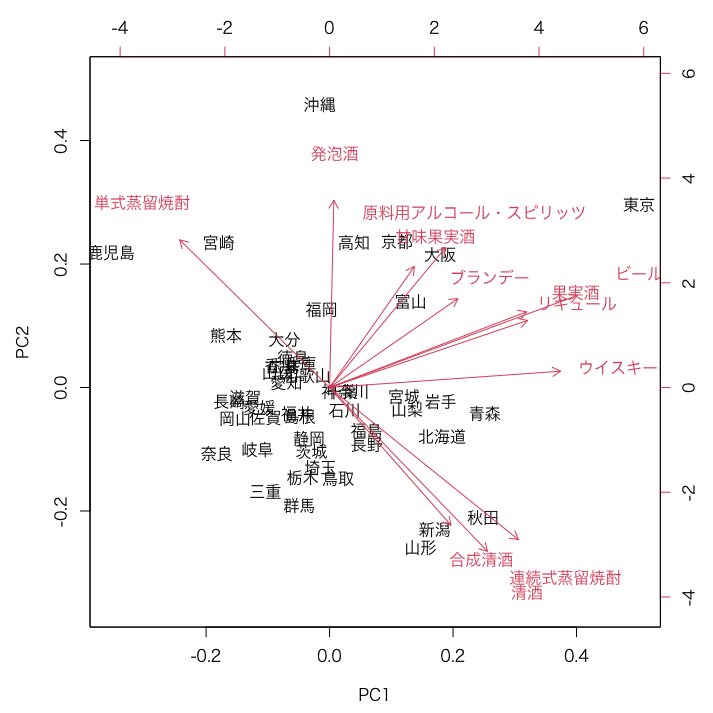
12次元(12列)の酒類の数量データが2次元に圧縮され、興味深い結果が得られました。
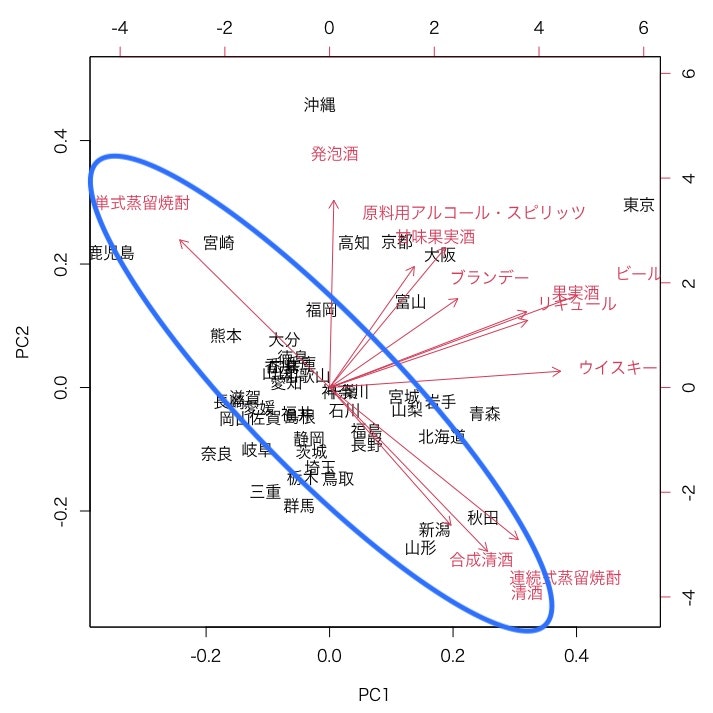
焼酎の軸(単式・連続式)
すぐに目に着くのは焼酎の軸です。単式蒸留焼酎と連続式蒸留焼酎がそれぞれ対極になっています。
左上に伸びているのは単式蒸留焼酎、右下に伸びているのが連続式蒸留焼酎です。
前者は九州の「鹿児島・宮崎」、後者は東北の「新潟・秋田・山形」が強い傾向にあるようです。
※単式蒸留焼酎と連続式蒸留焼酎
単式蒸留焼酎は原料の特徴が残るため 米・麦・さつまいもなどの焼酎となり、連続式蒸留焼酎はクセのない味わいのためキンミヤ焼酎など、サワー等の割材として使われます。
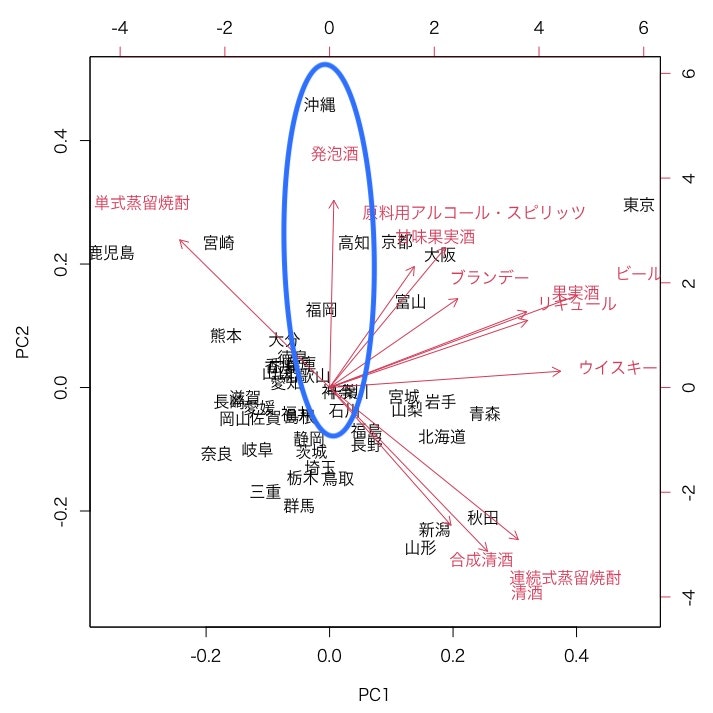
沖縄と発泡酒
沖縄は他の地域と比較して発泡酒が消費されやすい傾向にあるようです。
宮崎や鹿児島に近い方向に位置しているのは、泡盛(単式蒸留焼酎)の影響かもしれません、
東京の多様性
東京は果実酒(ワイン等)、ブランデー、リキュール、ビール、ウイスキーなど醸造酒・蒸留酒ともに幅広く消費される傾向にあるようです。
おわりに
主成分分析によって情報縮約し各都道府県のポジショニングを可視化することができましたが、もしかすると今回の内容は因子分析(Factor Analysis)の方が適切だったのかもしれません。というのも都道府県の消費傾向は背後に複数の因子(気候、平均所得、文化の多様性 等の違い)が考えられるからです。
実際に酒類と気温の相関を示すデータもあるようです。
沖縄では暑さによって発泡酒が好まれ、東北では寒さによって日本酒が好まれる ということはありそうです。
勉強も兼ねて主成分分析前提で進めてみたものの、やはり多変量解析はなかなか難しい世界だと実感しました。
参考URL・講座