mediba Advent Calendar 2021の21日目です。
この記事では、「ガチャの抽選」を例にとって、Rにおける二項分布の関数を整理してみます。
「当選(1%)と当選以外(99%)からなるベルヌーイ試行のガチャの抽選(復元抽出)を100回繰り返す」として話を進めていきます。
二項分布とは
何かを行ったときに起こる結果が2つしかない試行をベルヌーイ試行と呼び、互いに独立したベルヌーイ試行に従う確率分布のことを二項分布(The Binomial Distribution)と言います。
数学において、二項分布(にこうぶんぷ、英: binomial distribution)は、結果が成功か失敗のいずれかである試行(ベルヌーイ試行と呼ばれる)を独立に n 回行ったときの成功回数を確率変数とする離散確率分布である。
二項分布 - Wikipedia
計算式
期待値: $E(X) = np$
分散 : $V(X) = np(1-p)$
以下の式では「確率$p$で成功する試行を独立に$n$回繰り返した場合の、$k$回成功する確率」を求めることができます。
$P(X = k) = {}_n C_k p^k (1-p)^{n-k}$
また、二項分布$B(n,p)$は、$n$が十分に大きいときには平均$np$・分散$np(1-p)$の正規分布に近似することができます。
Rの関数
Rでは二項分布に関して以下の関数が用意されています。
| 関数名 | 内容 |
|---|---|
| rbinom(n, size, prob) | 二項分布からサンプルを抽出。(Random generation for the binomial distribution) |
| qbinom(p, size, prob) | 二項分布のパーセント点。分位点関数 (Quantile function) |
| dbinom(x, size, prob) | 成功回数がちょうど x回となる確率。確率密度(Density)。 |
| pbinom(q, size, prob) | 成功回数が q回以下 or q回より上 である確率(Probability)。分布関数 (Distribution function) |
そしてそれぞれの引数は以下の通りです。
| パラメータ | 内容 |
|---|---|
| n | 出力する乱数の数 |
| size | 試行する回数 |
| prob | 各試行における、成功が発生する確率 |
| p | 確率 |
| x,q | 成功が発生する回数 |
| lower.tail | 確率に関して、TRUEの場合にはP[X ≤ x]、FALSEの場合にはP[X > x]となる |
では実際に、これらの関数をガチャの抽選を例として利用してみることにします。
1) 個々の試行の当選回数をシミュレートする (rbinom)
今回のガチャの抽選(100回の試行)を100回繰り返し、それぞれの当選回数を求めてみます。
rbinom(n, size, prob)は「成功確率がprobの試行をsize回実施して、それをn回繰り返し、それぞれの成功した数」を返します。
rbinom(100,100,0.01)
> [1] 1 1 1 0 1 0 0 1 3 0 0 0 3 2 1 1 1 0 2 0 0 2 1 2 1 0 1 0 0 0 0 0 3
> [34] 0 0 1 1 0 0 1 1 1 0 1 2 1 1 0 1 0 1 2 2 1 1 0 2 1 0 2 0 1 4 2 1 1
> [67] 1 1 0 1 1 0 2 0 1 2 2 1 0 0 2 3 0 3 1 0 0 1 1 1 0 2 1 0 3 1 0 2 1
> [100] 1
100回分の繰り返しの結果(当選回数)が返ってきました。0と1が多いようですが、稀に4もあるようです。
乱数を羅列しただけでは分かりづらいので、table()で成功回数ごとの合計を集計してみます。
rbinom(10,100,0.01) %>%
table()
> 0 1 2 3 4
> 36 41 16 6 1
1が41回で一番多く、次に0が36回です。「36%は一回も当選しない」という意外な結果となりました。
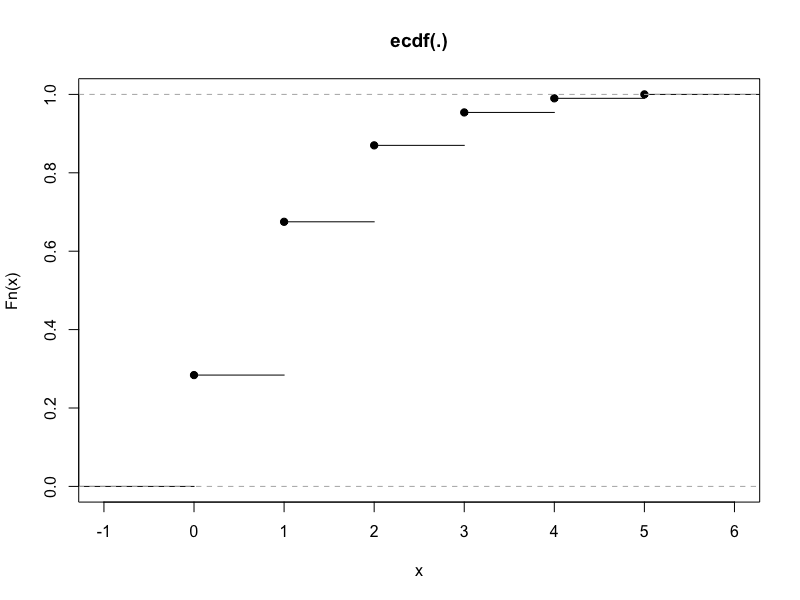
Rではecdf()にて経験分布関数としてプロットすることも可能です。
rbinom(10,100,0.01) %>%
ecdf() %>%
plot()
2) 任意の累積確率の分位点を求める (qbinom)
今回のガチャにおける「累積確率が50%、80%でのそれぞれの分位点」を求めてみます。
qbinom(p,size,prob)は「成功確率がprobの試行をsize回行ったときの、累積確率がpの分位点」を返します。
qbinom(0.5,100,0.01)
> [1] 1
qbinom(0.8,100,0.01)
> [1] 2
「累積確率が50%点では成功回数が1回以下」「累積確率が80%点では成功回数が2回以下」という感じでしょうか。
3) ちょうど1回当選する確率を求める (dbinom)
今回のガチャにおける「ちょうど1回当選する確率」を求めてみます。
dbinom(x,size,prob)は「成功確率がprobの試行をsize回行ったときの、成功がちょうどx回発生する確率」を返します。
dbinom(1,100,0.01)
[1] 0.3697296
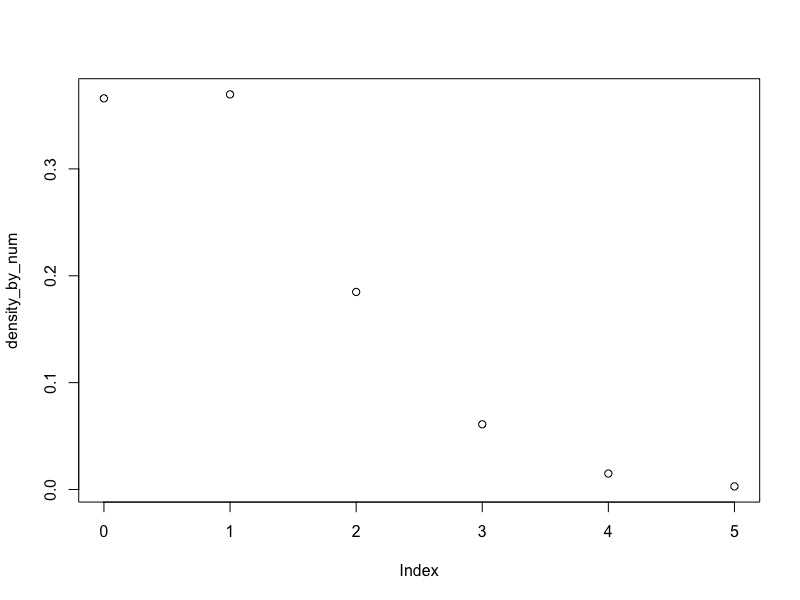
ちょうど1回当選する確率は約37%となりました。さらに当選回数ごとの確率を求めてプロットしてみます。
success_num <- seq(0, 5, by = 1)
density_by_num <- dbinom(success_num,100,0.01)
# success_numは0から始まるが、plotの軸はindex番号(1)から始まるため、x軸に任意の値を設定
plot(density_by_num, xaxt="n")
xact_name = c("0","1","2","3","4","5")
axis(1,1:6,labels=xact_name)
0回と1回がそれぞれ約37%で、2回が約20%となり3回以降から大幅に減っていきます。
4) 1回以上当選する確率を求める (pbinom)
「ちょうどn回成功する確率(dbinom)」ではなく「n回以上成功する確率」に関心がある場合にはpbinom()が利用できます。
今回のガチャにおける「1回以上当選する確率」を求めてみます。
pbinom(q,size,prob,lower.tail = FALSE)は「成功確率がprobの試行をsize回行ったときの、成功がq回よりも大きい値で発生する確率」を返します。
ここでは「0回よりも大きい値(=1回以上)」として実行してみます。
pbinom(0,100,0.01,lower.tail = FALSE)
[1] 0.6339677
rbinom()でシミュレートした結果とほぼ同じで、1回以上当選する確率は63%となりました。
※ 引数qよりも大きい値における総和を求めたい場合はlower.tailをFALSEで設定します。q以下の値における総和を求めたい場合はlower.tailをTRUEで設定します。(または省略します)
200回抽選してみる
さすがに200回も抽選すれば1回以上当選する確率は大幅に上がるのではないでしょうか。試行回数を増やして試してみます。
pbinom(0,200,0.01,lower.tail = FALSE)
> [1] 0.8660203
200回抽選してもまだ86%という意外な結果になりました。
300回抽選してみる
せっかくなのでもう少し回してみましょう。
pbinom(0,300,0.01,lower.tail = FALSE)
> [1] 0.9509591
ここまできてようやく95%まで到達しました。
おわりに
Rではrbinom()で「乱数数抽出」、qbinom()で「任意の分位点」、dbinom()で「ちょうどn回成功する確率」、pbinom()で「n回より多く成功する確率」を求めることができました。
そしてpbinom()の実行結果では、当選確率1%の試行を100回実施しても「1回以上当選する確率が63%(=1回も当選しない確率が37%)」ということが分かりました。
つまり復元抽出においては「当選確率1%のガチャを100回抽選しても37%の確率で一度も当選せず、200回抽選しても14%、300回抽選しても5%は当選しない」ことになります。
1%という数字が明示された上で300回抽選しても当たらなかったら、さすがにインチキではないかと疑ってしまいそうです。(事実、NPSの自由回答やアプリストアのレビューでも「抽選の当たりづらさ」に関連するコメントは散見されます。)
確率は人間の直感に反することもあり、なかなか難しい世界です。