熱伝導方程式(または拡散方程式やその他のスカラー輸送方程式)を有限差分法で解くとき,陽解法,クランクニコルソン法,完全陰解法の 3 手法がよく用いられる.
ここでは完全陰解法に触れる.
完全陰解法は次のような特性を持つ:
- 時間刻みが細かいときはクランクニコルソン法に精度で劣る
- 時間刻みが粗いときでも現実的な(不自然に振動しない)解をもたらす
- 陽解法に比べて格段に複雑だが,クランクニコルソン法に比べてわずかに単純である
- (陽解法と異なり)時間刻みの細かさによらず安定である
端的に換言すれば,「それっぽい解を,少ない計算量で,安定して出せる」.
熱伝導方程式
先に記号の一覧を載せておく.
| 記号 | 物理量 | 次元 | SI 単位(参考) |
|---|---|---|---|
| $T$ | 温度 | $\mathsf\Theta$ | $\mathrm K$ |
| $x$ | 位置 | $\mathsf L$ | $\mathrm m$ |
| $t$ | 時刻 | $\mathsf T$ | $\mathrm s$ |
| $k$ | 熱伝導率 | $\mathsf M;\mathsf L;\mathsf T^{-3};\mathsf\Theta^{-1}$ | $\mathrm W/(\mathrm m;\mathrm K)$ |
| $\rho$ | 密度 | $\mathsf M;\mathsf L^{-3}$ | $\mathrm{kg}/\mathrm m^3$ |
| $c$ | 比熱 | $\mathsf L^2;\mathsf T^{-2};\mathsf\Theta^{-1}$ | $\mathrm J/(\mathrm{kg};\mathrm K)$ |
| $S$ | 発熱速度 | $\mathsf M;\mathsf L^{-1};\mathsf T^{-3}$ | $\mathrm W/\mathrm m^3$ |
ここでは次のような熱伝導を考える:
- 対流がない
- 一直線上の一次元熱伝導
- 熱伝導率 $k$ は一様でないかもしれないが温度 $T$ に依存しない
- 容積比熱 $\rho c$ は一様でないかもしれないが温度 $T$ に依存しない
- 発熱速度 $S$ は位置 $x$ に依存するかもしれない
- 発熱速度 $S$ は温度 $T$ に依存しないか,または $T$ の一次関数で表せる
- 周期境界条件がない
このとき熱伝導方程式は
\rho(x) c(x) \frac{\partial T(x, t)}{\partial t}
= \frac{\partial}{\partial x} \left[k(x) \frac{\partial T(x, t)}{\partial x}\right] + S(x, T) \tag{1}
と書ける.
離散化
空間の離散化
有限差分法では,解析領域を細かい部分(コントロールボリューム,以降 CV と表記する)に区切り,各 CV にそれを代表する格子点を設ける.
そして,各格子点の温度を計算することによって,解析領域内の温度分布を明らかにすることを目指す.
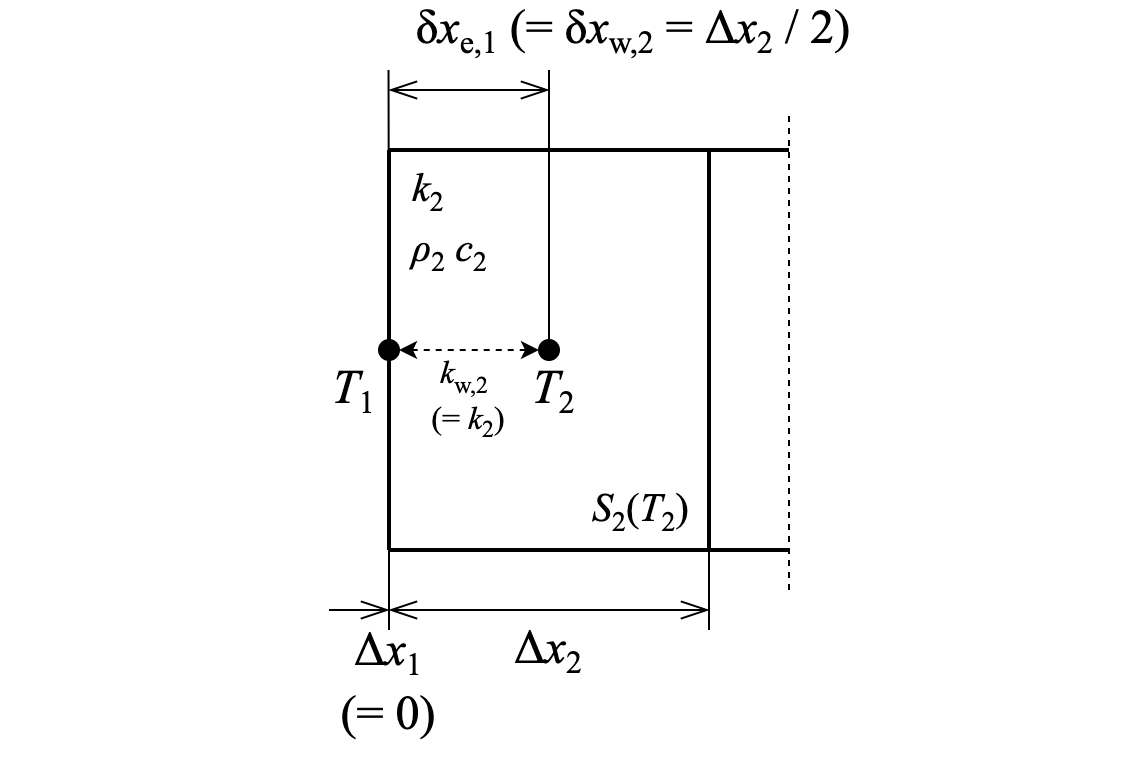
格子点を各 CV の中心に置くことにすると,解析領域内部の CV はこのようになる:
ただし,添字の $i$ は,$i$ 番目の CV または格子点における値であることを意味する.
また,添字の $\text{e}$,$\text{w}$ は $x$ 軸に関する正の側・負の側を表している.
$\Delta x$ は CV の幅,$\delta x$ は格子点間の距離である.
各 CV は必ずしも同じ幅である必要はない.
$k_{\text{e}}$ と $k_{\text{w}}$ は格子点間の実質的な熱伝導率である.
境界以外では $k_{\text{e}, i} = k_{\text{w}, i+1}$ が成り立つ.
隣接する CV の熱伝導率が一致するならば単にその値を当てはめればいいが,そうでない場合には長さを重みとして調和平均を取る:
\begin{align}
\frac{{\Delta x_i / 2 + \Delta x_{i+1} / 2}}{k_{\text{e}, i}}
&= {\frac{\Delta x_i / 2}{k_i} + \frac{\Delta x_{i+1} / 2}{k_{i+1}}} \\
k_{\text{e}, i} &= \frac{\left(\Delta x_i + \Delta x_{i+1}\right) k_i k_{i+1}}
{\Delta x_{i+1} k_i + \Delta x_i k_{i+1}} \tag{2}
\end{align}
解析領域の端(境界)については,幅がゼロであるような CV を置くことにする.
この CV は,境界条件を適用するときの厄介事を押しつけるのに役立つ.
左端の境界上に,幅がゼロである 1 番目の CV を置いたときの状況はこのようになる:
完全陰解法における時間の離散化
境界以外の CV
完全陰解法の離散化方程式は,もとの熱伝導方程式(1)に似せて書けば
\rho_i c_i \frac{T_i - T_i^0}{\Delta t}
= \frac{1}{\Delta x_i} \left[k_{\text{e}, i} \frac{T_{i+1} - T_i}{\delta x_{\text{e}, i}}
- k_{\text{w}, i} \frac{T_i - T_{i-1}}{\delta x_{\text{w}, i}}\right] + S_i(T_i) \tag{3}
となる.ただし $T_i$,$T_{i+1}$,$T_{i-1}$ は今から計算しようとしている未知の値である.そして $T_i^0$ は直前の時間ステップで計算した過去の $T_i$(最初の時間ステップでは初期温度)を表し,これは既知である.
式(3)を次のように変形する:
\begin{alignat}{1}
\frac{\rho_i c_i \Delta x_i}{\Delta t} \left(T_i - T_i^0\right)
= &\frac{k_{\text{e}, i}}{\delta x_{\text{e}, i}} \left(T_{i+1} - T_i\right)
-\frac{k_{\text{w}, i}}{\delta x_{\text{w}, i}} \left(T_i - T_{i-1}\right) \\
&+ S_i(T_i) \Delta x_i
\end{alignat} \tag{4}
すると各項の意味付けとして
- 左辺は $i$ 番目の CV の温度変化に要する熱
- 右辺第 1 項は $(i+1)$ 番目の CV から $i$ 番目へ流入する熱
- 右辺第 2 項は $i$ 番目の CV から $(i-1)$ 番目へ流出する熱
- 右辺第 3 項は $i$ 番目の CV 内部での発熱
と考えることができ,式全体としては $i$ 番目の CV の熱エネルギー収支を表すことになる.
ここで,$i$ 番目の CV における発熱速度 $S_i$ が格子点温度 $T_i$ の一次関数で表せると仮定し,次のように書く:
S_i(T_i) \Delta x_i = S_{\text{C}, i} + S_{\text{P}, i} T_i \tag{5}
ただし $S_i$ が温度に依存しないときは $S_{\text{P}, i} = 0$ として差し支えない.
さらに
\begin{align}
a_{\text{E}, i} &= \frac{k_{\text{e}, i}}{\delta x_{\text{e}, i}} \tag{6} \\
a_{\text{W}, i} &= \frac{k_{\text{w}, i}}{\delta x_{\text{w}, i}} \tag{7} \\
a_{\text{P}, i}^0 &= \frac{\rho c \Delta x_i}{\Delta t} \tag{8} \\
b_i &= S_{\text{C}, i} + a_{\text{P}, i}^0 T_i \tag{9} \\
a_{\text{P}, i} &= a_{\text{E}, i} + a_{\text{W}, i}
+ a_{\text{P0}, i} - S_{\text{P}, i} \tag{10}
\end{align}
と置くと,離散化方程式(4)は
\begin{align}
a_{\text{P}, i}^0 \left(T_i - T_i^0\right)
&= a_{\text{E}, i} \left(T_{i+1} - T_i\right)
- a_{\text{W}, i} \left(T_i - T_{i-1}\right) \\
&\phantom{=.} + S_{\text{C}, i} + S_{\text{P}, i} T_i \\
\left(a_{\text{E}, i} + a_{\text{W}, i}
+ a_{\text{P}, i}^0 - S_{\text{P}, i}\right)T_i
&= a_{\text{E}, i} T_{i+1} + a_{\text{W}, i} T_{i-1}
+ S_{\text{C}, i} + a_{\text{P}, i}^0 T_i^0 \\
a_{\text{P}, i} T_i
&= a_{\text{E}, i} T_{i+1} + a_{\text{W}, i} T_{i-1}
+ b_i \tag{11}
\end{align}
と整理できる.
境界上の CV
解析領域の境界に置いた CV には,上述した式(5–10)をそのまま用いることができず,境界条件に応じたパラメータが必要になる.
よくある境界条件では,式(11)を左端の CV ($i = 1$)について成り立たせるためのパラメータは以下のようになる:
| 左端の境界条件 | $a_{\text{E}, 1}$ | $a_{\text{W}, 1}$ | $a_{\text{P}, 1}^0$ | $S_{\text{C}, 1}$ | $S_{\text{P}, 1}$ |
|---|---|---|---|---|---|
| 温度が $T_\text{BC}$ で一定 | $0$ | $0$ | $0$ | $T_\text{BC}$ | $-1$ |
| 断熱 | $a_{\text{W}, 2}$ | $0$ | $0$ | $0$ | $0$ |
| 熱流束が $q_x$ で一定 | $a_{\text{W}, 2}$ | $0$ | $0$ | $q_x$ | $0$ |
| 外部温度が $T_\infty$ で熱伝達率が $h$ | $a_{\text{W}, 2}$ | $0$ | $0$ | $h T_\infty$ | $-h$ |
| 外部温度が $T_\infty$ で熱抵抗が $r$ | $a_{\text{W}, 2}$ | $0$ | $0$ | $T_\infty/r$ | $-1/r$ |
$b_1$ と $a_{\text{P}, 1}$ は境界以外の CV のときと同じく式(9, 10)に従う.
$a_{\text{P}, 1}^0$ も特別扱いする必要はない($\Delta x_1 = 0$ だから式(8)は自動的にゼロとなる).
右端の CV にも同様にして境界条件を適用できるが,CV の番号や添え字の $\text{E}$ と $\text{W}$ を適宜読み替えることになる.
離散化方程式の解法
それぞれの CV について式(11)が成り立つので,格子点と同数の一次方程式が連立していることになる:
a_{\text{P}, i} T_i = a_{\text{E}, i} T_{i+1}
+ a_{\text{W}, i} T_{i-1} + b_i
\quad (i = 1, 2, 3, \ldots, N) \tag{12}
ここで $N$ は格子点の総数である.
$T_0$ や $T_{N+1}$ は存在しないので $a_{\text{W}, 1} = 0$,$a_{\text{E}, N} = 0$ とする.
それぞれの時間ステップにおいて,次の時刻における各格子点の温度を計算するために,この連立方程式を解く必要がある.
これは三重対角行列アルゴリズム(TriDiagonal Matrix Algorithm, TDMA)により線形時間で解ける:
- $P_1 = a_{\text{E}, 1} / a_{\text{P}, 1}$
- $Q_1 = b_1 / a_{\text{P}, 1}$
- $\displaystyle
P_i = \frac{a_{\text{E}, i}}{a_{\text{P}, i} - a_{\text{W}, i} P_{i-1}},
Q_i = \frac{b_i+a_{\text{W}, i} Q_{i-1}}
{a_{\text{P}, i} - a_{\text{W}, i}P_{i-1}}
\quad (i = 2, 3, 4, \ldots, N)$ - $T_N = Q_N$
- $T_i = P_i T_{i+1} + Q_i\quad (i = N, N-1, N-2, \ldots, 1)$
順に右辺を計算して左辺に代入していけば,
最終的に新しい温度分布 $T_i ; (i = 1, 2, 3, \ldots, N)$ が得られる.
計算例
熱伝導方程式のパラメータと境界条件
解析領域の左端が $x = 0$,右端が $x = 1$ となるように位置 $x$ を定めた.
各パラメータは必ずしも一様ではないと仮定したが,運よくそれらが一様であり,さらに発熱速度が温度に依存しない場合:
\begin{alignedat}{2}
k&(x) &&= 1.0 = \text{const.} \\
\rho&(x) &&= 1.0 = \text{const.} \\
c&(x) &&= 1.0 = \text{const.} \\
S&(x, T) &&= 1.0 = \text{const.}
\end{alignedat}
について,温度分布変化を計算してみた.
初期温度は一様に $0$,左側の境界温度は $0$,右側の境界は断熱とした:
T(x, 0) = 0, \; T(0, t) = 0, \; \left.\left[-k(x)\frac{\partial T(x, t)}{\partial x}\right]\right|_{x = 1} = 0
なお,このときの定常状態($\partial T/\partial t = 0$)における温度分布は解析的に解くことができる:
T(x) = \frac{1}{2} \frac{S}{k} x (2-x) = \frac{1}{2} x (2-x)
CV の幅と時間刻み
ここでは解析領域を $25$ 個の CV に等分してみた.
境界の CV を含めると $27$ 個の CV を置いたことになる.
境界以外の CV の幅は,一律に $\Delta x = 1/25 = 0.04$ である.
そして $\Delta t = 0.1$ とし,$3$ 秒後までの温度分布変化を計算した.
ちなみに,陽解法では数値的安定性を得るために $\Delta t \leq \rho c (\Delta x)^2 / (2k) = 0.0008$ という条件が課される.
今回は,$3$ 秒後の温度分布の算出を,陽解法の $1/100$ 以下のループ回数で済ませようとしていることになる.
結果
精度については定量的に検討しないが,現実的な挙動で定常解に接近していくことが分かる.
ソースコード
Fortran で作ったついでに Julia 版も作ってみた.
熱伝導率や発熱速度が一様でない問題についても,配列 K や S_C の値を変更すれば対応できる.
(言い換えれば,それらを一様とみなしてよい場合にはこのソースコードは冗長である.)
Fortran
module therm
implicit none
! Dimensions
! L : Length
! T : Time
! M : Mass
! Theta: Absolute temperature
! E : Energy (= M L^2 / T^2)
double precision, parameter :: DT = 1.0d-1 ! Time step [T]
double precision, parameter :: T_MAX = 3.0d0 ! Time to stop iteration [T]
integer, parameter :: NX_INNER = 25 ! Number of CVs, excluding the zero-width boundary CVs
integer, parameter :: NX = NX_INNER + 2 ! Number of CVs
! Boundary and initial temperatures [Theta]
double precision, parameter :: TEMP_WEST = 0.0d0
double precision, parameter :: TEMP_INIT = 0.0d0
integer, private :: xi
! Material properties
double precision, parameter :: K(NX) = 1.0d0 ! Thermal conductivity [E/(L T Theta)]
double precision, parameter :: RHO(NX) = 1.0d0 ! Density [M/L^3]
double precision, parameter :: CAP(NX) = 1.0d0 ! Specific heat capacity [E/(M Theta)]
! Volumetric heat source
double precision, parameter :: SRC_C(NX) = 1.0d0 ! Constant part [E/(L^3 T)]
double precision, parameter :: SRC_P(NX) = 0.0d0 ! Proportional part coef. [E/(L^3 T Theta)]
! CV widths [L]
double precision, parameter :: DX(NX) = [0d0, (1d0 / NX_INNER, xi = 2, NX-1), 0d0]
! Grid point positions [L]
double precision, parameter :: X(NX) = [(sum(DX(1:xi)) - DX(xi) * 0.5d0, xi = 1, NX)]
! Distances between adjacent grid points [L]
double precision, parameter :: DIST_X(NX-1) = X(2:) - X(:NX-1)
! Conductivities between adjacent grid points [E/(L T Theta)]
double precision, parameter :: K_E(NX-1) = (DX(:NX-1) + DX(2:)) * K(:NX-1) * K(2:) &
& / (DX(2:) * K(:NX-1) + DX(:NX-1) * K(2:))
double precision :: temp(NX) = TEMP_INIT ! Temperature distribution [Theta]
! East neighbour coefs. [E/(L^2 T Theta)]
double precision, parameter :: A_E(NX) = [0d0, K_E(2:) / DIST_X(2:), 0d0]
! West neighbour coefs. [E/(L^2 T Theta)]
double precision, parameter :: A_W(NX) = [0d0, K_E(:NX-2) / DIST_X(:NX-2), K_E(NX-1) / DIST_X(NX-1)]
! Inertia coefs. [E/(L^2 T Theta)]
double precision, parameter :: A_P0(NX) = RHO * CAP * DX / DT
! Source constants [E/(L^2 T)]
double precision, parameter :: S_C(NX) = [TEMP_WEST, SRC_C(2:NX-1) * DX(2:NX-1), 0d0]
! Source coefs. [E/(L^2 T Theta)]
double precision, parameter :: S_P(NX) = [-1d0, SRC_P(2:NX-1) * DX(2:NX-1), 0d0]
! Centre-point coefs. [E/(L^2 T Theta)]
double precision, parameter :: A_P(NX) = A_E + A_W + A_P0 - S_P
! Constant terms [E/(L^2 T)]
double precision :: b(NX)
end module therm
module solver
implicit none
contains
pure subroutine solve_tridiagonal(solution, a, b, c, d)
! Tridiagonal matrix algorithm
! Solve
! a[i]*T[i] = b[i]*T[i+1] + c[i]*T[i-1] + d[i]
! i = 1, 2, 3, ..., N
! for T
!
! N is the length of `solution`
! b[N] and c[1] have no effect
double precision, intent(out) :: solution(:)
double precision, intent(in) :: a(:)
double precision, intent(in) :: b(:)
double precision, intent(in) :: c(:)
double precision, intent(in) :: d(:)
double precision :: p(size(solution)-1)
double precision :: q(size(solution))
integer :: n
integer :: i
n = size(solution, 1)
p(1) = b(1) / a(1)
q(1) = d(1) / a(1)
do i = 2, n-1
p(i) = b(i) / (a(i) - c(i) * p(i-1))
q(i) = (d(i) + c(i) * q(i-1)) / (a(i) - c(i) * p(i-1))
end do
q(n) = (d(n) + c(n) * q(n-1)) / (a(n) - c(n) * p(n-1))
solution(n) = q(n)
do i = n-1, 1, -1
solution(i) = p(i) * solution(i+1) + q(i)
end do
end subroutine solve_tridiagonal
end module solver
program main
use therm
use solver
implicit none
double precision, parameter :: OUTPUT_INTERVAL_TIME = 5.0e-1 ! [T]
integer , parameter :: OUTPUT_INTERVAL_LOOPS = nint(OUTPUT_INTERVAL_TIME / DT)
integer :: ti
call export_distr(temp)
do ti = 1, nint(T_MAX / DT)
b = S_C + A_P0 * temp
call solve_tridiagonal(temp, A_P, A_E, A_W, b)
if (mod(ti, OUTPUT_INTERVAL_LOOPS) == 0) call export_distr(temp)
end do
contains
subroutine export_distr(temp_distr)
double precision, intent(in) :: temp_distr(:)
integer :: unit
integer :: xi
open (newunit = unit, file = "temp_distr_fortran.dat", position = 'append', action = 'write')
do xi = 1, NX
write (unit, '(F14.10, ES24.15E3)') X(xi), temp_distr(xi)
end do
write (unit, '(A1)') new_line('A') ! Insert two blank lines to separate datasets
close (unit)
end subroutine export_distr
end program main
Julia
# Harmonic mean of two values, weighted
harmonic(a, b, w_a, w_b) = (w_a+w_b) * a * b / (w_b*a + w_a*b)
module Therm
# Dimensions
# L : Length
# T : Time
# M : Mass
# Theta: Absolute temperature
# E : Energy (= M L^2 / T^2)
import Main: harmonic
export DT, T_MAX, NX, TEMP_INIT, X, A_E, A_W, A_P0, A_P, S_C
const DT = 1.0e-1 # Time step [T]
const T_MAX = 3.0e0 # Time to stop iteration [T]
const NX_INNER = 25 # Number of CVs, excluding the zero-width boundary CVs
const NX = NX_INNER + 2 # Number of CVs
# Boundary and initial temperatures [Theta]
const TEMP_WEST = 0.0
const TEMP_INIT = 0.0
# Material properties
const K = fill(1.0, NX) # Thermal conductivity [E/(L T Theta)]
const RHO = fill(1.0, NX) # Density [M/L^3]
const CAP = fill(1.0, NX) # Specific heat capacity [E/(M Theta)]
# Volumetric heat source
const SRC_C = fill(1.0, NX) # Constant part [E/(L^3 T)]
const SRC_P = fill(0.0, NX) # Proportional part coef. [E/(L^3 T Theta)]
const DX = vcat(0.0, [1.0 / NX_INNER for xi in 2:NX-1], 0.0) # CV widths [L]
const X = [sum(DX[1:xi-1]) + DX[xi] * 0.5 for xi in 1:NX] # Grid point positions [L]
const DIST_X = X[2:NX] - X[1:NX-1] # Distances between adjacent grid points [L]
# Conductivities between adjacent grid points [E/(L T Theta)]
const K_E = harmonic.(K[1:NX-1], K[2:NX], DX[1:NX-1], DX[2:NX])
# East neighbour coefs. [E/(L^2 T Theta)]
const A_E = vcat(0.0, K_E[2:NX-1] ./ DIST_X[2:NX-1], 0.0)
# West neighbour coefs. [E/(L^2 T Theta)]
const A_W = vcat(0.0, K_E[1:NX-1] ./ DIST_X[1:NX-1])
# Inertia coefs. [E/(L^2 T Theta)]
const A_P0 = RHO .* CAP .* DX / DT
# Source constants [E/(L^2 T)]
const S_C = vcat(TEMP_WEST, SRC_C[2:NX-1] .* DX[2:NX-1], 0.0)
# Source coefs. [E/(L^2 T Theta)]
const S_P = vcat(-1.0, SRC_P[2:NX-1] .* DX[2:NX-1], 0.0)
# Centre-point coefs. [E/(L^2 T Theta)]
const A_P = A_E + A_W + A_P0 - S_P
end
function solve_tridiagonal!(solution, a, b, c, d)
# Tridiagonal matrix algorithm
# Solve
# a[i]*T[i] = b[i]*T[i+1] + c[i]*T[i-1] + d[i]
# i = 1, 2, 3, ..., N
# for T
#
# N is the length of `solution`
# b[N] and c[1] have no effect
n = length(solution)
p = similar(solution, n-1)
q = similar(solution)
p[1] = b[1] / a[1]
q[1] = d[1] / a[1]
for i in 2:n-1
p[i] = b[i] / (a[i] - c[i] * p[i-1])
q[i] = (d[i] + c[i] * q[i-1]) / (a[i] - c[i] * p[i-1])
end
q[n] = (d[n] + c[n] * q[n-1]) / (a[n] - c[n] * p[n-1])
solution[n] = q[n]
for i in n-1:-1:1
solution[i] = p[i] * solution[i+1] + q[i]
end
end
using .Therm
function main()
OUTPUT_INTERVAL_TIME = 5.0e-1 # [T]
OUTPUT_INTERVAL_LOOPS = round(OUTPUT_INTERVAL_TIME / DT)
temp = fill(TEMP_INIT, NX) # Temperature distribution [Theta]
export_distr(temp)
for ti in 1:round(T_MAX / DT)
b = S_C + A_P0 .* temp # Constant terms [E/(L^2 T)]
solve_tridiagonal!(temp, A_P, A_E, A_W, b)
if mod(ti, OUTPUT_INTERVAL_LOOPS) == 0
export_distr(temp)
end
end
end
using Printf
function export_distr(temp)
out_file = open("temp_distr_julia.dat", "a")
for xi in 1:NX
@printf(out_file, "%14.10f %24.14E\n", X[xi], temp[xi])
end
print(out_file, "\n\n") # Insert two blank lines to separate datasets
close(out_file)
end
main()
補足
本記事中で量記号として用いている文字のほとんどはパタンカーの本に整合するようにしている.
例外的に,本記事における $S_\text{C}$,$S_\text{P}$ はそれぞれパタンカーの本における $S_C \mathit\Delta x$,$S_P \mathit\Delta x$ に相当する.
本記事の問題設定は,直接法で現実的に解ける範囲で,極力タチの悪いものにしている.
これより厄介な問題(二次元以上の場合,発熱速度と温度との関係が非線形である場合など)を考える場合は,TDMA と反復法を組み合わせるなりして解く必要がある.
参考文献
- スハス V. パタンカー 原著,水谷幸夫・香月正司 訳,コンピュータによる熱移動と流れの数値解析,森北出版,1985 年,ISBN 978-4-627-91190-1