背景
近接露光を用いたパターン形成を最近やっているのですが,具体的な光強度が気になり始めました。調べてみたところ,以下のようなプログラムが既にある模様。
- 近接露光計算プログラム:http://skomo.o.oo7.jp/f54/hp54_1.htm
こちらをそのまま使用してもよかったのですが,Excel経由したくないなーとか,計算領域もっと分割したいなーとか思ったので,科学計算に強いと聞くPythonで実装してみることにしました。
実装にあたっては,上記のものを参考にしています。
フレネル回折とは
スリット-スクリーン間の距離が小さいときに生じる回折現象です。
スリットが単一矩形の場合,スクリーン上における光の波動 $U(P_n)$ はスリット面における光の波動 $U(S_n)$ を用いて以下のようにシンプルに表されます。
U(P_n)=\frac{U(S_n)}{2\mathrm{i}}\left[\int_{v_1}^{v_2}\exp\left(\frac{\pi v^2}{2}\mathrm{i}\right)dv\right]\left[\int_{w_1}^{w_2}\exp\left(\frac{\pi w^2}{2}\mathrm{i}\right)dw\right]
変数変換は以下のように行われています。
なお,スクリーン上の座標を $x$ と $y$ ,スリット開口部の座標を $\xi$ と $\eta$ ,光の波長を $\lambda$,スリット-スクリーン間の距離を $b$ で示しました。
v = \sqrt{\frac{2}{\lambda b}}(\xi - x)
w = \sqrt{\frac{2}{\lambda b}}(\eta - y)
上の積分を解こうとすると面倒くさいやつ(フレネル積分)が現れますが,scipy.specialモジュールを使うことでシンプソン則を用意せずに済むそうです。便利。
実装
※ガバコード注意報※
import numpy as np
from scipy.special import fresnel
import matplotlib.pyplot as plt
# 露光条件の定義
WL = 0.365 # 波長(μm)
gap = 5 # スリット-スクリーン間の距離(μm)
INA = 0 # 光の広がり角度(rad)
X1 = -5 # 計算領域のX方向最小値(μm)
X2 = 5 # 計算領域のX方向最大値(μm)
Nx = 100 # 計算領域のX方向分割数
Y1 = -100 # 計算領域のY方向最小値(μm)
Y2 = 100 # 計算領域のY方向最大値(μm)
Ny = 200 # 計算領域のY方向分割数
Pr = 1 # スリット面の光の実数部
Pi = 0 # スリット面の光の虚数部
Px1 = -0.5 # 矩形パターンのX方向最小値(μm)
Px2 = 0.5 # 矩形パターンのX方向最大値(μm)
Py1 = -50 # 矩形パターンのY方向最小値(μm)
Py2 = 50 # 矩形パターンのY方向最大値(μm)
# 計算領域の作成
dx = (X2 - X1) / Nx
dy = (Y2 - Y1) / Ny
Xaxis = np.arange(X1, X2, dx)
Ysaxis = np.arange(Y1, Y2, dy)
Yaxis = np.c_[Ysaxis]
Isum = np.zeros((Ny, Nx))
# フレネル積分
def cal_f(t1, t2):
s1, c1 = fresnel(t1)
s2, c2 = fresnel(t2)
dif_s = s2 - s1
dif_c = c2 - c1
return dif_s, dif_c
# 光強度の計算
def cal_int(ox, oy):
fx1 = lambda x: np.sqrt(2 / (WL * gap)) * (Px1 - x - ox)
fx2 = lambda x: np.sqrt(2 / (WL * gap)) * (Px2 - x - ox)
fy1 = lambda y: np.sqrt(2 / (WL * gap)) * (Py1 - y - oy)
fy2 = lambda y: np.sqrt(2 / (WL * gap)) * (Py2 - y - oy)
vfx1 = np.vectorize(fx1)
vfx2 = np.vectorize(fx2)
vfy1 = np.vectorize(fy1)
vfy2 = np.vectorize(fy2)
vf_int = np.vectorize(cal_f)
asv, acv = vf_int(vfx1(Xaxis), vfx2(Xaxis))
asw, acw = vf_int(vfy1(Yaxis), vfy2(Yaxis))
ar = (acv * asw + asv * acw) / 2
ai = (asv * asw - acv * acw) / 2
ur = Pr * ar - Pi * ai
ui = Pr * ai + Pi * ar
li = (np.power(ur, 2) + np.power(ui, 2))
return li
# 光の広がりの考慮
i = -5
k = 0
while i <= 5:
j = -5
while j <= 5:
if i ** 2 + j ** 2 <= 25:
k += 1
Ox = i * gap * INA / 5
Oy = j * gap * INA / 5
Isub = cal_int(Ox, Oy)
Isum = Isum + Isub
j += 1
else:
j += 1
else:
i += 1
Iave = Isum / k
# グラフ描画
plt.rcParams['font.size'] = 18
plt.rcParams['font.family'] = 'sans-serif'
plt.tight_layout()
plt.imshow(Iave, extent=[X1, X2, Y1, Y2], aspect='auto', interpolation='nearest', cmap='jet')
plt.xlabel('x-position (μm)')
plt.ylabel('y-position (μm)')
plt.colorbar()
plt.clim(0, 1.0)
plt.grid(True)
plt.show()
試行
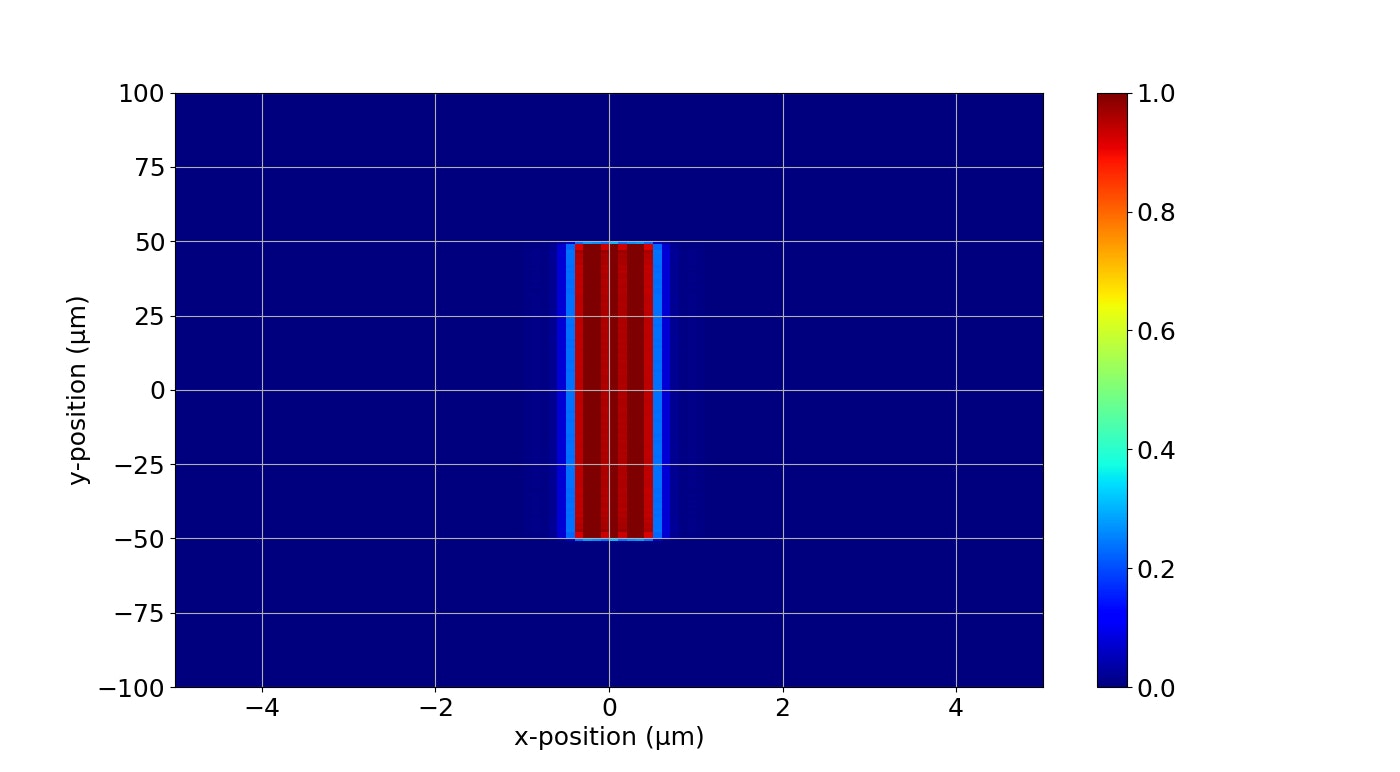
コード記載の条件で,スリット-スクリーン間の距離を色々変えてスリット幅1 μmの露光状態を確認してみました。
[0.1 μm]
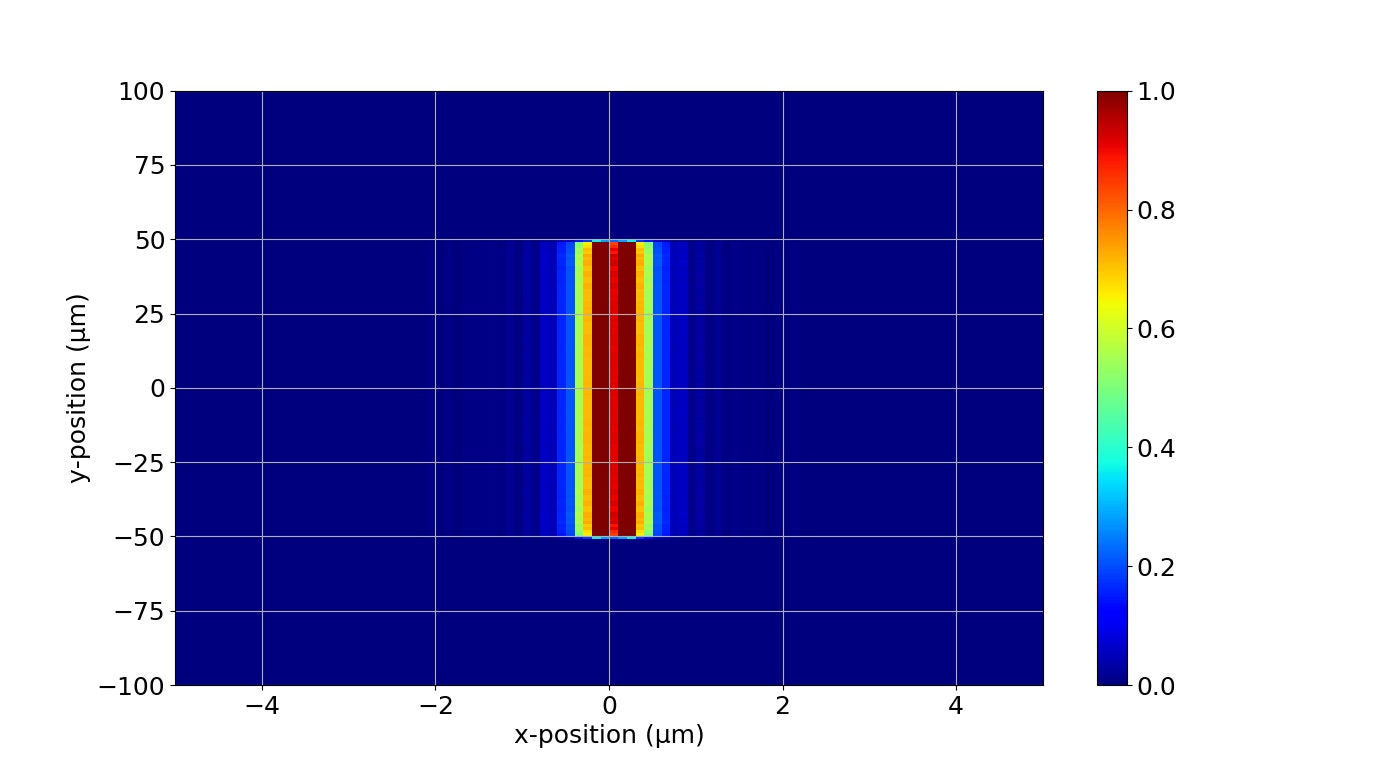
[0.5 μm]
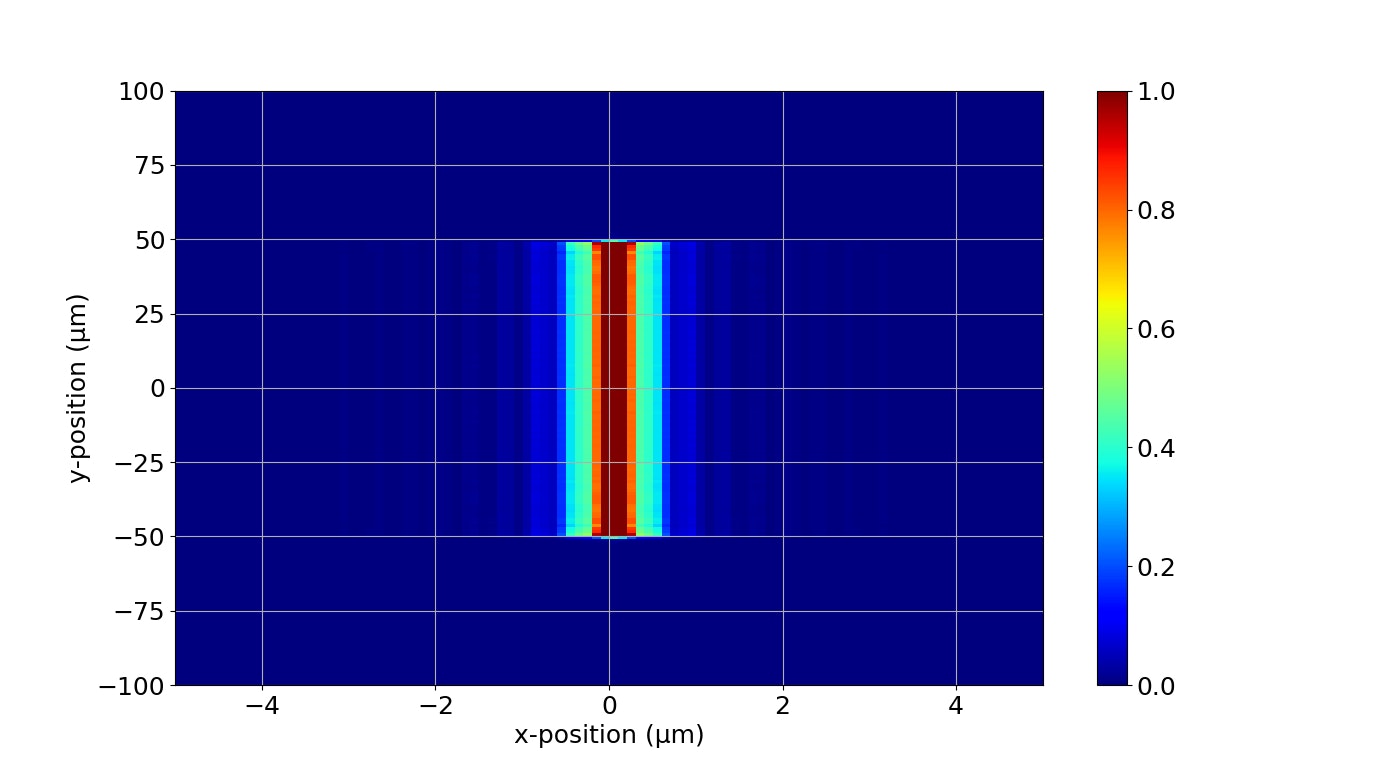
[1 μm]
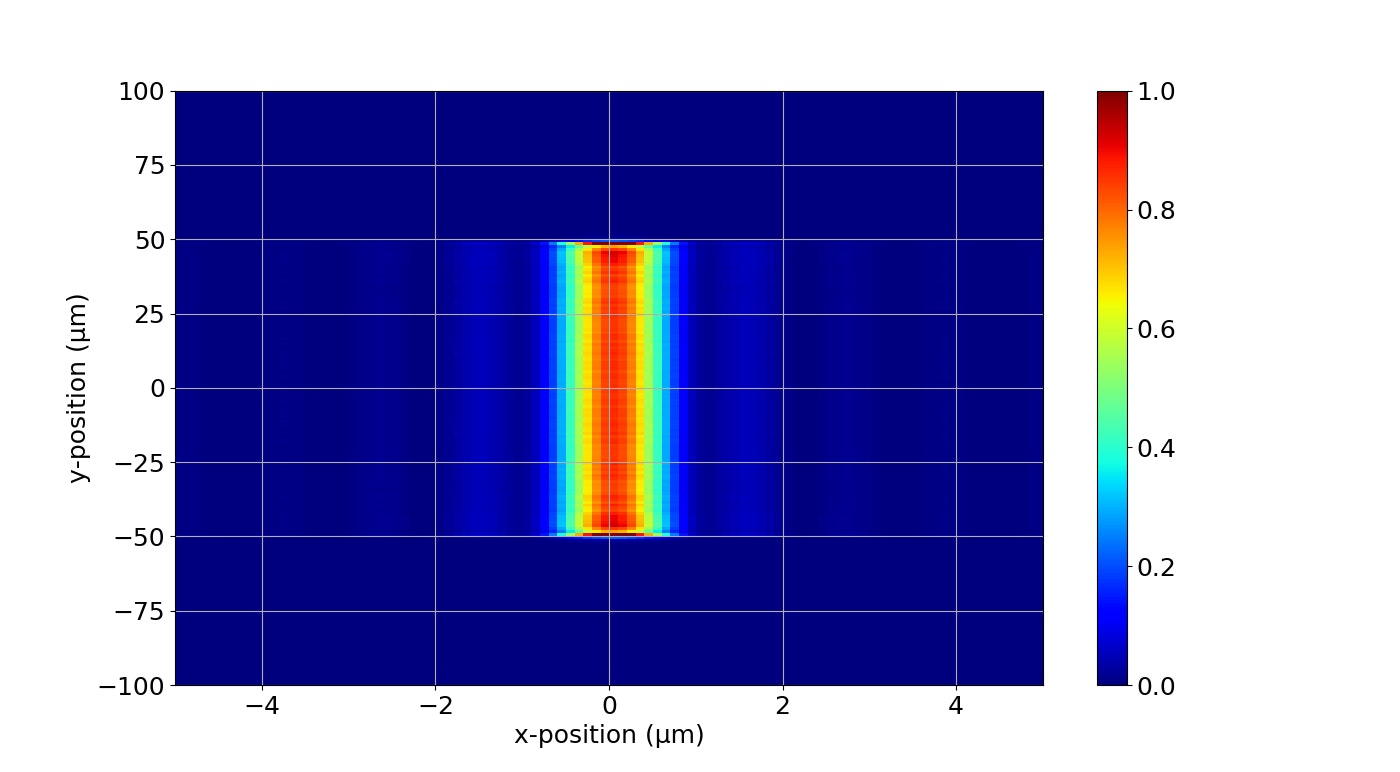
[3 μm]
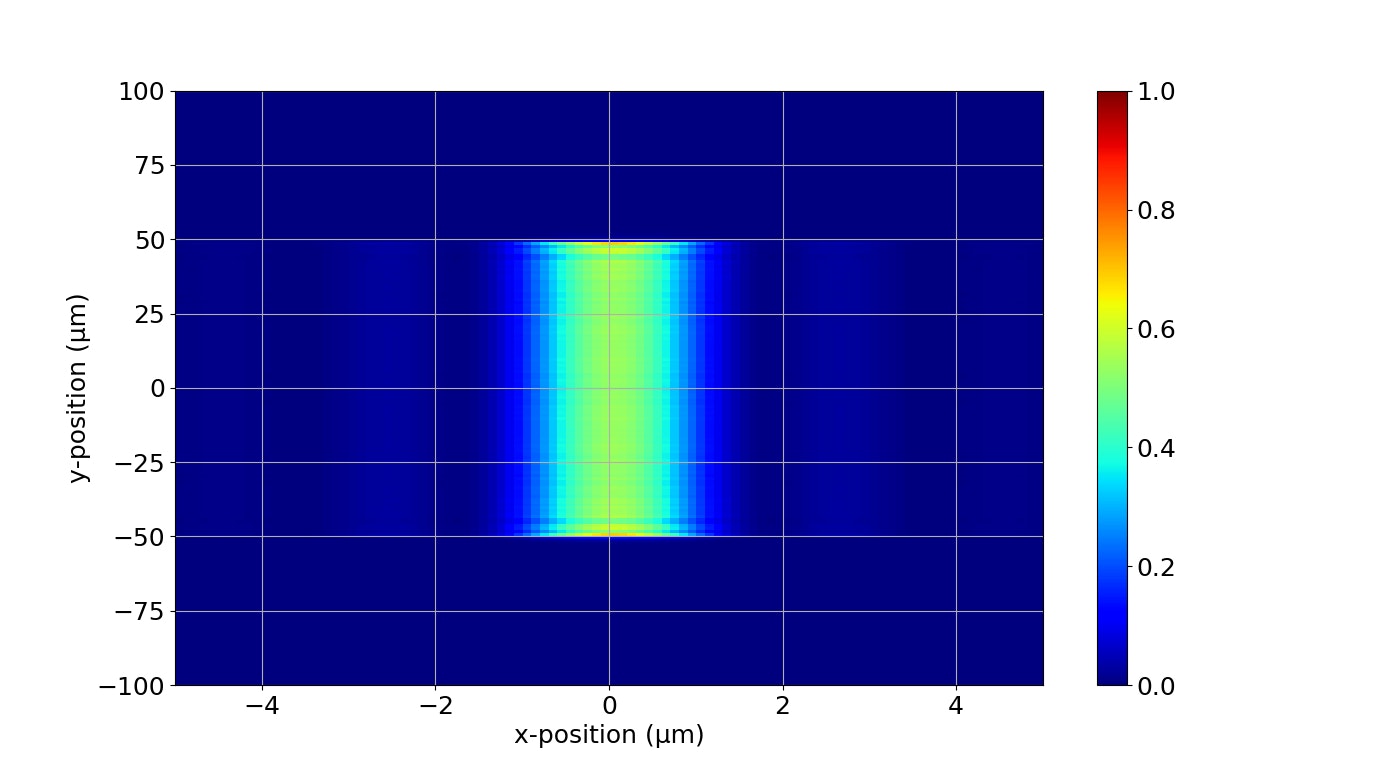
[5 μm]
1 μm以降のx方向への広がりがやばいですね。中央部の強度もかなり下がっています。
プロキシミティ露光はともかく,コンタクト露光でもハードコンタクトをかなり意識しないと厳しそうということが分かります。
おわりに
今回は単一矩形のみでしたが,任意のパターンについても今後できたらいいなーと思います。