はじめに
paiza問題集 二分探索 値の検索(PHP編)を解いたので二部探索について自分用にまとめる。
二分探索法とは?
探索の代表的なアルゴリズムの一つ。
探索対象のデータ群が***「昇順」または「降順」***に並んでいる場合に使用できる。
二分探索法は、データ群をざっくりと二つに分けながら対象を絞り込んでいく探索法。
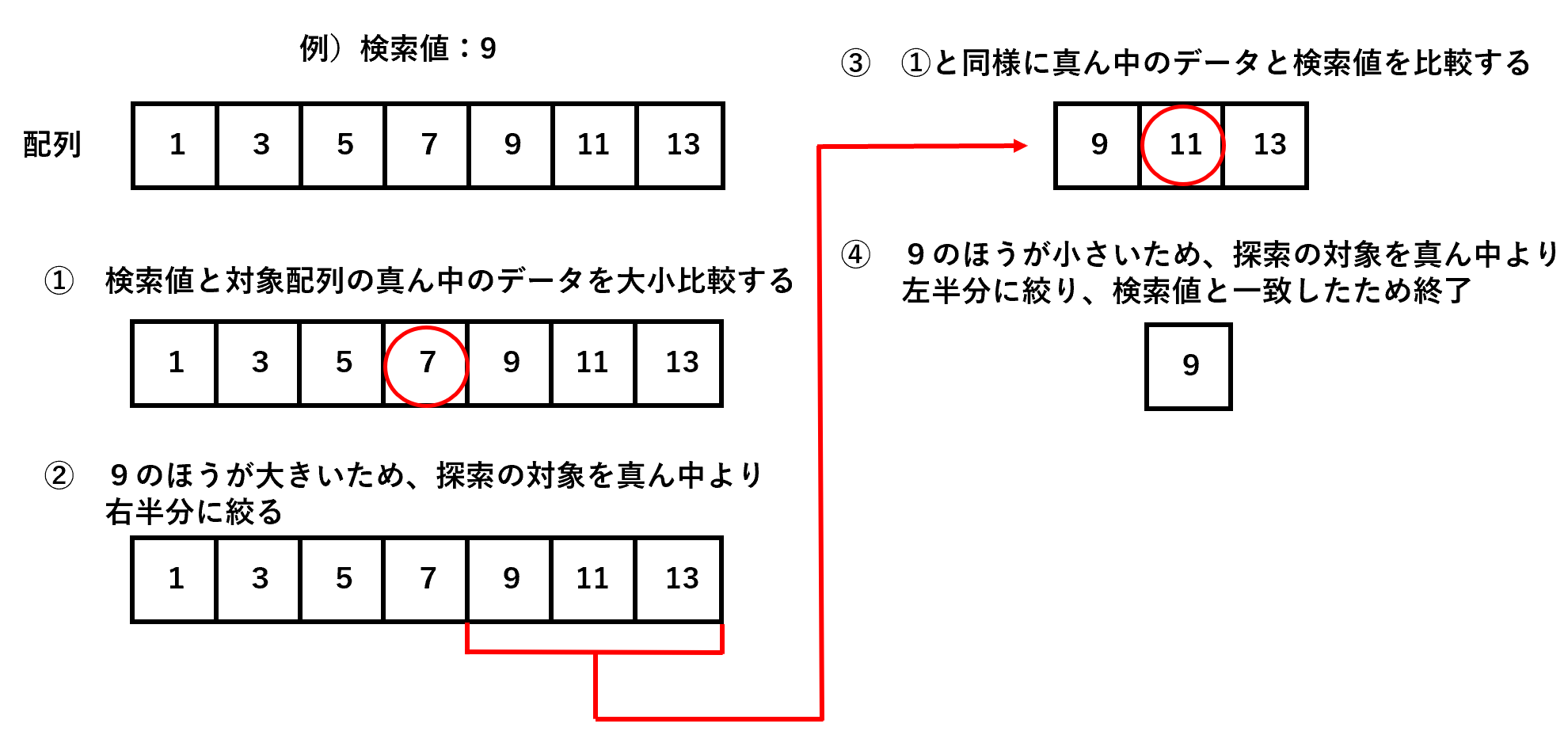
上記画像の例で説明すると
まず、配列の真ん中の値である「7」と今回検索したい「9」を大小比較する。
9のほうが大きいため、探索範囲を右半分に絞る。
次の探索範囲の真ん中の値である「11」と検索したい「9」を大小比較する。
9のほうが小さいため、探索範囲を左半分に絞る。
このように繰返し真ん中の値と比較して範囲を狭めていき対象を絞り込む。
そのため、昇順あるいは降順であらかじめソートされていないとこの探索法は使えない。
参考
・キタミ式イラストIT塾 基本情報技術者 平成31/01年
(Capter16-8 データを探索するアルゴリズム)
実際の問題
〇問題文
ソートされた数列 A = (A_1, A_2, ..., A_n) と、q 個の整数 k_1, k_2, ..., k_q が与えられます。各 k_i について、数列 A に含まれているなら Yes と、含まれていないなら No と出力してください。
なお、n, q の最大値はいずれも 200,000 です。
〇条件
・ 入力はすべて整数
・ 1 ≦ n ≦ 200,000
・ -10^9 ≦ A_i ≦ 10^9 (1 ≦ i ≦ n)
・ A_1 ≦ A_2 ≦ ... ≦ A_n
・ 1 ≦ q ≦ 200,000
・ -10^9 ≦ k_i ≦ 10^9 (1 ≦ i ≦ q)
今回、nとqは最大200000個まで存在するということなので、もし線形探索法で行うと計算量がO(n)であるため、最大200000 × 200000 回処理をする必要がある。
→そこで二部探索法を使用する。
〇計算量
線形探索法 O(n)
二分探索法 O(logn)
実装
//入力値の取得
$n = trim(fgets(STDIN));
$array = explode(' ', trim(fgets(STDIN)));
$q = trim(fgets(STDIN));
//二分探索
for ($i = 0; $i < $q; $i++) {
$left = 0;
$right = $n-1;
$value = trim(fgets(STDIN)); //検索したい値
$flag = false;
while ($left <= $right) {
$mid = floor(($left + $right) / 2);
if ($array[$mid] == $value) {
$flag = true;
break;
} elseif ($array[$mid] < $value) {
//検索したい値が真ん中のデータより大きい場合、左端の範囲を更新する
$left = $mid + 1;
} else {
//検索したい値が真ん中のデータより小さい場合、右端の範囲を更新する
$right = $mid - 1;
}
}
if ($flag) {
echo "Yes";
} else {
echo "No";
}
echo "\n";
}
まとめ
今回は二部探索法の問題を解いた。
基本情報で昔勉強したことを思い出した。実際にコードを書いてみるとより理解が深まって勉強になった。
Paizaの問題でレートが上がってくると、データ量が多くなってきて線形探索では規定時間内に処理が終わらないため、様々なアルゴリズムについて引き続き学習していきたい。