More than 5 years have passed since last update.

初心者のための測度論的確率論 ~ Pythonコードを添えて ~

Last updated at 2018-09-12Posted at 2018-08-27

測度論的確率論をの初歩的な部分を、コードも交えながら気持ち優先で解説したいと思います。
自分の勉強内容のアウトプットも兼ねています。

##動機
技術的な書籍を読んでいて、確率という概念を自分の中できちんと整理したいと思うようになったこと、そしてそれをアウトプットしたいと思ったことが動機です。
確率という概念は、機械学習やデータ分析、情報科学といった分野の基礎知識として多数用いられています。私の本職はネットワークエンジニアで、仕事でこの辺りに触れることはないのですが、流行りものが好きでよくこの手の入門書に手を出しては休日に眺めています。
しかし、その中でどうしても気になっていることが1つあります。
それは、多くの書籍で確率という概念が非常に曖昧に用いられていることです。特に、確率変数、確率分布という言葉の定義がかなり曖昧に済まされている場合が多いと感じています。
数式を用いた論理展開を主軸にしたような書籍でも、根っ子にあたるはずの確率変数と確率分布という言葉は、かなりモヤっとした感じで定義しているものが多い印象です。そして、そういった曖昧な言葉を土台にしてそれ以降の内容が積み上げられているので、いつまでたってもモヤモヤした気持ちを抱えていました。
この状態を払拭すべく、いつか腰を据えて確率論の基礎を整理する必要があると感じてはいたのですが、これが結構難しく、中々手が進みませんでした。
最近になって、ようやく基本的なことが頭の中で整理されてきて、自分の言葉でまとめられるようになってきた気がするため、その内容を形に残そうと思うに至りました。

##構成
この文章は次のような構成で記述するように努めます。
・必要な概念の定義
　ここは形式的な言葉で、出来るだけきちんと厳密に書くつもりです。
・概念が意図する気持ち
　ここは出来るだけ自分の言葉で、かなりラフに書くつもりです。
・概念を実装するPythonコード(一部のみ)
　書けそうな部分はPythonコードで書くことに挑戦します。
　数式よりもコードを見た方が理解しやすいという人もいるかもしれないというのが意図です。

##想定読者
・技術書などに出てくる確率という概念にモヤモヤを抱えていて、スッキリさせたい方¹

・確率・統計分野に対して全くの初見ではなく、少しでも触れたことのある方
・集合と写像の基本的な言葉遣いにある程度慣れている方
・私の理解に間違いがないかを探してくれて、あれば優しく指摘してくれる奇特な優しい方

##注意書き
・この文章は長いです。
・私は測度論、コーディングいずれも素人です。
　拙い記述やコードがあると思います、ツッコミやご指摘を頂けると大変うれしいです。
・気持ちの部分は、勉強を通して自分の脳内で思ったことを自分の言葉で書いています。
　ソースのないような考え・意見・持論もあります。
　大体合ってると信じてますが、盛大な見当違いをしている可能性を否定できません。

では本題に入ります。

##確率とは何か？
確率とは何でしょうか？
Wikipediaで調べると次のようなことが書いてあります。

確率（かくりつ、英: probability）とは、偶然性を持つある現象について、その現象が起こることが期待される度合い、あるいは現れることが期待される割合のことをいう。

また、次のようにも書いてあります。

日本工業規格では確率（かくりつ:probability）は、「ある試行を同じ条件の下で長く続けたとき，一定の結果が生起する相対頻度の極限値。より一般的にはランダムな事象に割り当てられている [0, 1] の範囲の実数値と定義される。一般に事象 A の確率を Pr (A)で表す。」参考として「ある事象が生じるという信念の度合いを表す主観確率という概念も存在する。」と定義している。

要するに、中学校で習った場合の数の比 (求める場合の数 ÷ 全ての場合の数) のことを言っているようです。どちらもランダム性に言及しているのがポイントです。
ランダムとは何でしょうか？ランダム性を用いた定義は、日常語として利用するには十分ですが、数学的な議論をするには扱いが難しいです。ランダムという概念は厳密に定義することが難しく、どうしてもモヤっとした定義にならざるを得ません。普段使いの会話では上のような定義で問題ないですが、数学的な議論に用いるには、文脈による語意の揺らぎを排除した厳密で定式的な定義が必要に感じます。日常語としての確率と、数学用語としての確率とは分けて考えた方が良さそうです。
数学用語としての確率とは何か？ということは、後程気持ちも交えて書こうと思います。
後で書きますが、うまくランダムという概念を切り離して定式化しています。

そのための準備として、恐らく最初の鬼門となる、可測空間というものをまず定義します。

##可測空間
可測空間を定義します。加速ではありません、可測です。
"○○の確率"という文章を考えます。"○○"の部分には、どのような言葉が入るでしょうか。どのような言葉でも良いのでしょうか。何かルールがあるのでしょうか。そのあたりを少し考えてみます。

####定義 (可測空間)

$Ω$ を集合とする。$Ω$ の部分集合族 $\mathscr{A}$ が次の性質を満たすとき、$\mathscr{A}$ をシグマ加法族²と呼び、組 $(Ω, \mathscr{A})$ を可測空間と呼ぶ

$Ω$ は $\mathscr{A}$ の要素である
$A$ が $\mathscr{A}$ の要素ならば、$A$ の補集合 $A^{c}$ もまた $\mathscr{A}$ の要素である。
$\mathscr{A}$ の高々加算個の要素 $A_{1}, A_{2}, A_{3}, … $ に対して、合併 $\bigcup_{i=1}^{\infty}A_{i}$ もまた $\mathscr{A}$ の要素である

とのことき $\mathscr{A}$ の要素を事象と呼び、$\mathscr{A}$ の要素としての $Ω$ を全事象 と呼ぶ。

####可測空間の気持ち³

いきなり "$Ω$ を集合とする" などと突き放すような書き方ですが、難しく考える必要はなく、実用上は$Ω$は全ての事象のもとになる集合を表すと考えてください。
例えばコイン投げについて考えるときには、$Ω =$ { "表が出る", "裏が出る" } といった具合に、各事象のもととなる要素を集めた集合になります。サイコロ投げだったら { "1が出る", "2が出る", ... , "6が出る" } といった具合です。
そして、事象そのものは $Ω$ の部分集合で表現します。
例えば、サイコロ投げで "1の目がでる" という事象は { "1が出る" } というシングルトン⁴を使って表し、"偶数の目が出る" という事象は {"2の目が出る", "4の目が出る", "6の目が出る"} という集合で表します。

これらの事象を集めた集合族 (集合の集合=集合族) を $\mathscr{A}$ と書くことにしています。
後で確率について考えるときは、"サイコロを投げて偶数の目が出る" 確率というのは、"$\mathscr{A}$ の要素 { "2の目が出る", "4の目が出る", "6の目が出る" } についての確率を考えること、と思えばよいのです。
性質 1〜3 は、$\mathscr{A}$を事象の集合として採用するにあたって満たすべき最低限のルールを表しています。"○○の確率"の○○に入る言葉のルールです。(シグマ加法族は 1〜3 を満たせばどのような集合族でも良く、色々な集合族が事象の集合となりえます。実際の場面では、暗黙のうちに$Ω$の冪集合をシグマ加法族として使っていると思われる場合が多いような気がします)
ただ、上に挙げたような $Ω$ は事象の要素を集めた集合の形をしているので、実数などと違って計算をするのにいささか扱いづらいです。次の次の確率変数の節で、その辺りをうまく扱えるように工夫する話が出てきます。

####コード
集合と部分集合族を作ってみて、それをシグマ加法性をチェックする関数を書いてみます。
集合は frozenset型で表現することにしています。
(普通の set型だと集合族が書けない(?)ため)
また、入力 A が高々加算個の要素を持つような場合を想定しています。
(非加算個の要素を持つ場合は対応できません)

# シグマ加法性をチェックする関数
from itertools import product

def has_sigma_additivity(Omega: frozenset, A: frozenset):
    """
    Omega の部分集合族 A がシグマ加法性を満たすかどうかチェックする
    Args:
        Omega (frozenset) : 集合
        A (frozenset) : Omegaの部分集合族

    Returns:
        bool
    """
    if Omega not in A:
        # 性質１の確認
        return False
    for a in A:
        if Omega.difference(a) not in A:
            # 性質２の確認
            return False
    for n in range(len(A)):
        for subset_family in product(A, repeat=n):
            subset = frozenset()
            for a_i in subset_family:
                subset = subset.union(a_i)
                if subset not in A:
                    # 性質３の確認
                    return False
    return True

# OKパターン
>>> Omega = frozenset(["a","b","c","d","e"])
>>> A = frozenset([Omega,
                   frozenset([]),
                   frozenset(["a","b"]),
                   frozenset(["c","d","e"])])
>>> has_sigma_additivity(Omega, A)
True

# NGパターン
# frozenset(["c"]) と frozenset(["a","b"]) との合併が無い
>>> B = frozenset([Omega,
                   frozenset([]),
                   frozenset(["a","b"]),
                   frozenset(["c","d","e"]),
                   frozenset(["c"])])
>>> has_sigma_additivity(Omega, B)
False

これで、"事象" という、確率を考えるための大元の部分を定式化することができました。では次に、確率についてきちんと考えてみます。

##確率測度

確率測度を定義します。ここまでが理解できれば、測度論的確率論の最初の一山は越えたといってよいと思います。

####定義 (確率測度)
$(Ω, \mathscr{A})$ を可測空間とする。$\mathscr{A}$上の実数値関数 $P:\mathscr{A} \to \mathbb{R}$ が次の性質を満たすとき、関数$P$を確率測度と呼ぶ。

$P(Ω) = 1$ である
$P(∅) = 0$ である
$\mathscr{A}$ の高々加算個の要素 $A_{1}, A_{2}, A_{3}, … $ が、どの2つも共通部分を持たないならば、$P( \bigcup_{i=1}^{\infty} A_{i}) = \sum_{i=1}^{\infty} P(A_{i})$ である

また、事象 $A∈\mathscr{A}$ に対し、$P(A)$の値を、事象$A$が起こる確率と呼び、組 $( Ω , \mathscr{A} , P )$ を確率空間と呼ぶ。
(ちなみに 2,3 のみを満たす関数を、単に測度といいます)

####確率測度の気持ち
(長くなりました…。)
確率測度という言葉が出てきました。これは何でしょうか。
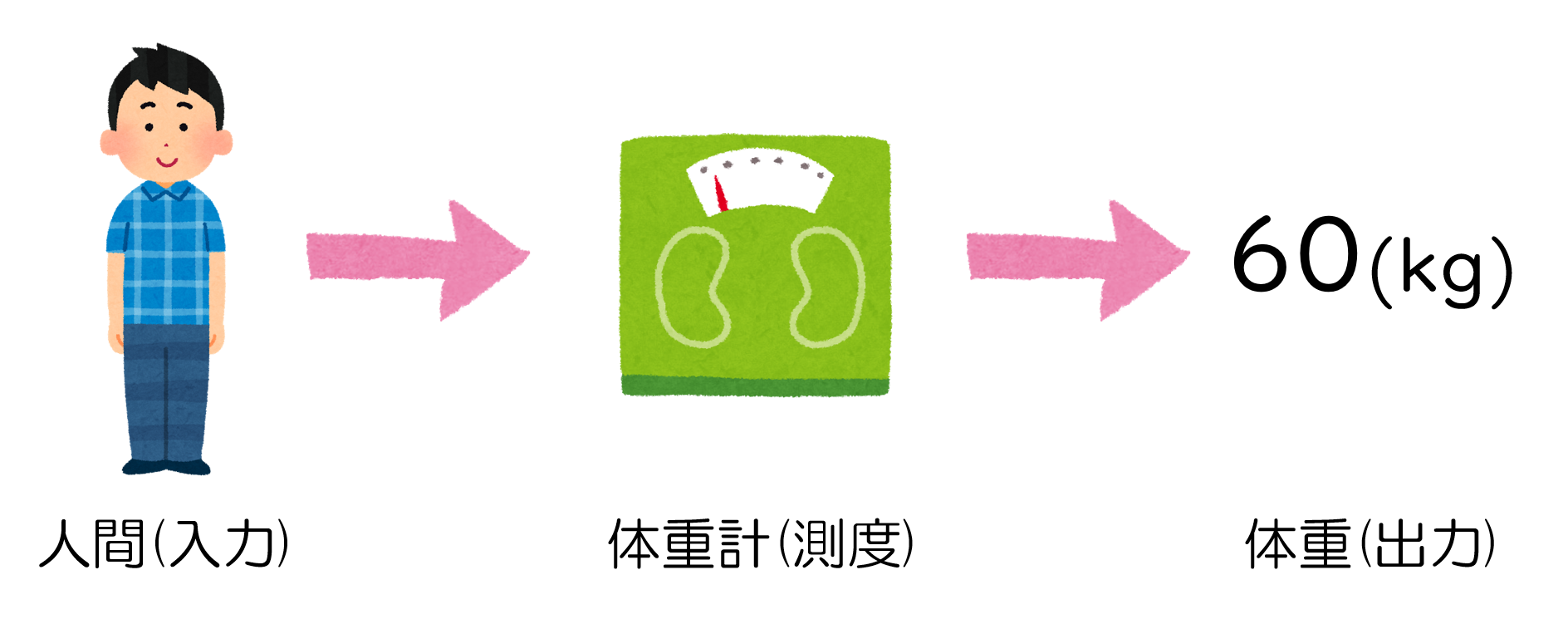
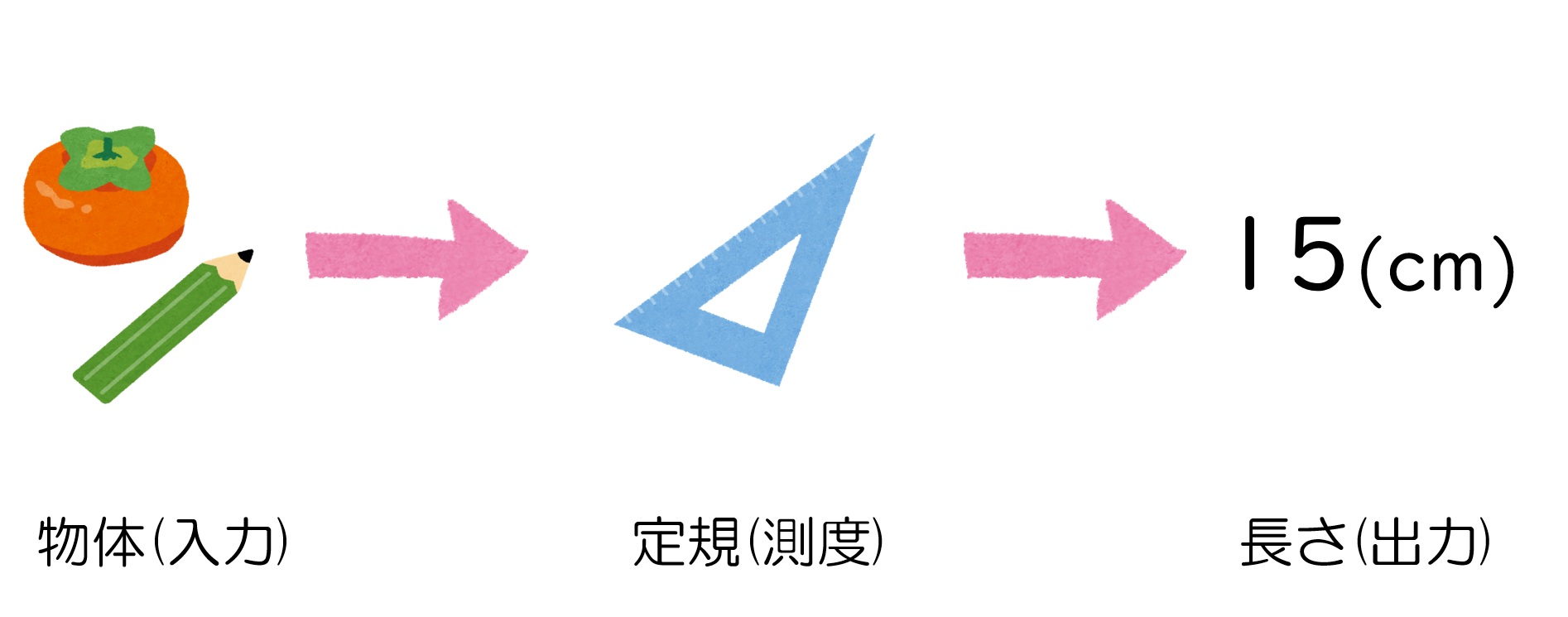
確率という言葉を抜いた、一般の測度について考えましょう。これは、ものすごくざっくりいうと、何かを測るための "物差し" を抽象化した概念です。
人間の体重を測るときは体重計を使いますし、モノの長さを測るときは定規やメジャーなどを使うと思いますが、そういった”モノの何か”を測るための道具を抽象化したのが測度です。そしてそれは、数学的には(上の条件を満たす)実数値関数として表現されます。
例えば体重計ならば、個々の人間を入力として、その人間の重量を数値として出力する関数として捉えることができます。定規ならば、何らかの物体(果物とか鉛筆とか...何でも良い)を入力として、その長さを数値として出力する関数と捉えることができます。

もしも、異なる2人の人間が同時に体重計に乗って出た数値が、別々に乗ったときの合計値よりも小さくなるような体重計があったら、その体重計は測度としては失格なのです(3つ目の条件を満たさないので)。
そして前節で出た可測空間の条件とは、測度を使って何かを測ることができるモノそのもののルールを規定していると捉えることができます。物差しは、それを使って個々のモノを測るだけではなく、モノが集まったモノ達(合併)についても同様に測ることが出来てほしいのです。つまり、モノを組み合わせたモノ達もまた測度の入力として許容したいという要件があります(さっきの体重計に2人乗る例のように)。そんなこと出来て当たり前だろと思うかもしれませんが、何も規定がなければ当たり前ではないのです。モノをどのように組み合わせたモノ達でもやはり同様に測ることができるように、可測空間の3つ目の条件があるのです。
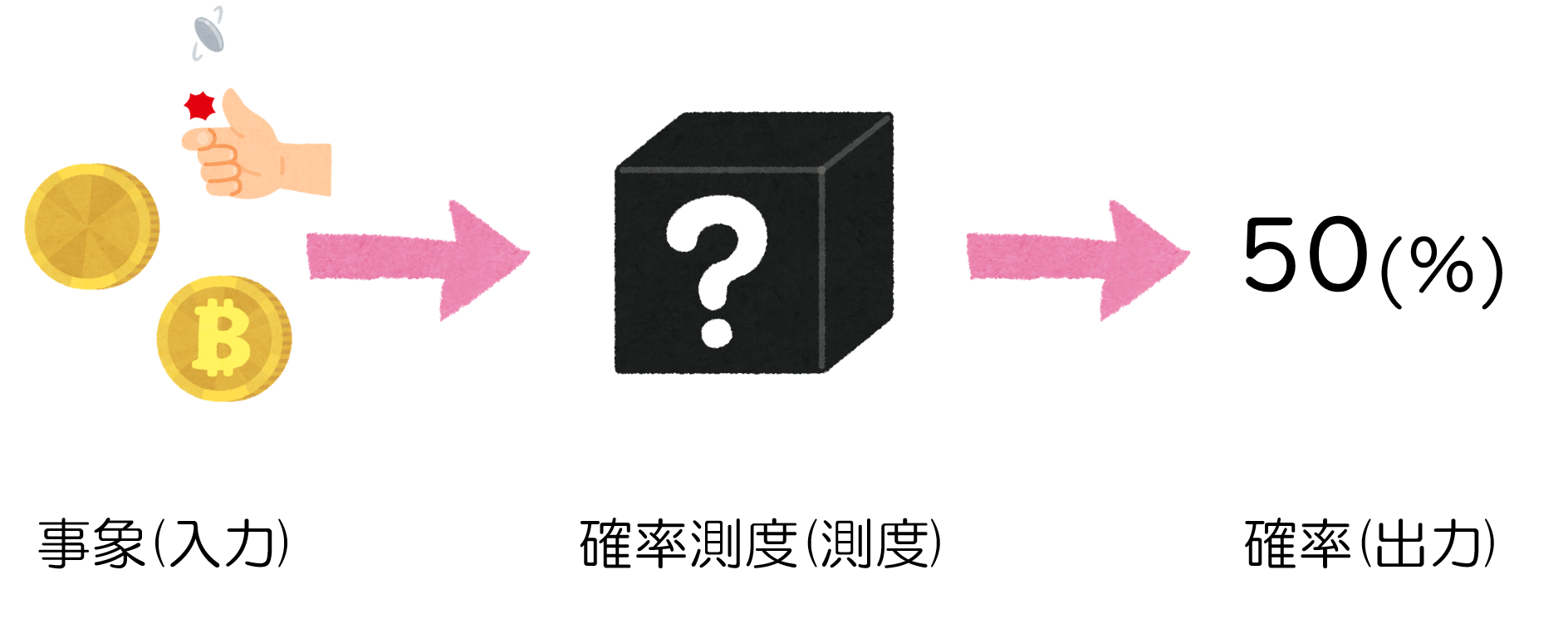
そして、確率測度は、"事象"というモノの、"確率"という数値を測るための物差しのことです。事象そのものを入力として、確率の値を出力する関数です。体重計や定規のように物理的な道具はないですが⁵、抽象化した概念としては同じように考えられます。

最初の疑問である、事象の確率とは何なのか？についての答えは、確率測度に事象を入力したときの出力の値のことです。

＊＊＊

ところで、ここまでの話には、具体的な確率の値をどのようにして与えるべきか？ということは出てきていません。
個人的にはここからが日常感覚とギャップがあるところだと思うのですが、具体的な確率の値をどのようにして与えるか、ということに関しては、数学は立ち入りません。 個々の事象に対してどのような値を与えるべきかについては、数学には何の規定もありません。それは数学の世界の外の話になります。
例えば、"コインを投げて表が出る確率" が具体的に何%であるべきか？という議論は、測度論の文脈では取り扱えず、数学の枠内では扱いません。

ではどうするかというと、それは人間が決めるのです。
過去の経験や、取得したデータから類推して決めるのです。
え？という思う人もいるかもしれませんが⁶、そうなのです。

上の例でいうと、"コインを投げて表が出る確率"というのは数学が決めることではなく、人間が決めることなのです。
同様に、"サイコロを投げて1の目が出る確率"というは、人間が決めることなのです。
"今日日本で生まれた赤ん坊の身長が、将来180cmを超える確率"は、人間が決めるなのことです。
もう少しちゃんと言うと "いま考えている確率変数が従う確率分布は何なのか？"という問題は、数学によって決めることではなく、過去の経験を参考にしたり、データを集めてその振舞いを調査したりした上で、適切と信じられるもの考えて、人間が決めるのです。⁷

「いやおかしい、コイン投げで表が出る確率は1/2だと学校で習ったじゃないか！あれは何だったんだ！」という意見があるかもしれません。
あれは実は、「各事象の出方は一様分布に従う」という前提が勝手に設定された世界だったのです。教科書のどこかに「ただし、各事象の出方は同様に確からしいとする…」という文言が書いてあったのを覚えていませんか？あれは、「とりあえず裏表が出る確率はそれぞれ等しく1/2ということにしときますよ！」ということを決めて宣言していたのです。その判断根拠は、多回数の試行や集めたデータの傾向だったり、経験と勘だったり状況によって様々ですが、結局は人間の都合で決めることです⁸。

しかし、そういった仮定をひとたび決めてしまえば、そこから先は数学を利用して様々な有用なことを知ることができるのです。例えば、"サイコロの各出目の確率は1/6だ"と決めてしまえば、"偶数の目が出る確率"や"4以上の目が出る確率"などは、経験や勘などではなく、数学の力で知ることができます[^9]。 [^9]: 各出目の事象の確率は 1/6 であると仮定すれば、偶数の目がでる事象は { "2の目が出る" , "4の目が出る" , "6の目が出る" } = { "2の目が出る" } $\cup$ { "4の目が出る" } $\cup$ { "6の目が出る" } なので、確率測度の性質3 から、 P( { "2の目が出る" } $\cup$ { "4の目が出る" } $\cup$ { "6の目が出る" } ) = P( { "2の目が出る" } ) + P( { "4の目が出る" } ) + P( { "6の目が出る" } ) = 1/6 + 1/6 + 1/6 = 1/2 として求まります。(4以上の... も同様です)

"コインの裏表の確率"を決めてしまえば、"10回連続で表が出る確率"なんかを知ることができます。
同様に、"日本の成人男性の身長は、平均170cm、分散36の正規分布に従う"と決めてしまえば、自分の子供が将来高身長になる確率を知ることができるでしょう。
市場や貨幣価値のトレンドがある特定の分布に従っているのだと決めてしまえば、数学の力でトレンドの波を完璧に予測でき、商品の売り上げアップや一攫千金を狙うことがきっとできるでしょう。最初に仮定として決めたことが完璧に正しければ、ですが。

コード

コイン投げを例に確率測度を作ってみて、それが確率測度になっていることをチェックする関数を書いてみます。

def is_measurement(Omega: frozenset, A: frozenset, P: "function"):
    """
    A 上の関数 P が可測空間(Omega, A)の確率測度になっているか判定する。
    Args:
        Omega (frozenset) : 集合
        A (frozenset) : Omegaの部分集合族
        P (function) : A上の確率関数

    Returns:
        bool
    """
    epsilon = 1e-10
    if abs(P(Omega) - 1) >= epsilon:
        # 性質１の確認
        return False
    if abs(P(frozenset())) >= epsilon:
        # 性質２の確認
        return False
    for n in range(2,len(A)):
        for subset_family in product(A, repeat=n):
            subet_family = set(subset_family)
            for a1, a2 in product(subset_family, repeat=2):
                intersection_flag = 0
                if a1 == a2:
                    continue
                if a1.intersection(a2):
                    intersection_flag = 1
                    break
            if intersection_flag == 1:
                continue
            subset = frozenset()
            P_sum = 0
            for a_i in subset_family:
                subset = subset.union(a_i)
                P_sum += P(a_i)
                if P(subset) - P_sum >= epsilon:
                    return False
    return True

# これまでの内容でコイントスをモデリングしてみる
>>> Omega_coin = frozenset(["表", "裏"])
>>> A_coin = frozenset({frozenset(),
                        frozenset({'表'}),
                        frozenset({'裏'}),
                        frozenset({'表', '裏'})})

# コイントスの確率を決める関数を作る
# OKパターン
def prob_of_coin_flip(a: frozenset):
    if a == frozenset(["表"]):
        return 99/100
    elif a == frozenset(["裏"]):
        return 1/100
    result = 0
    for i in a:
        result += prob_of_coin_flip(frozenset([i]))
    return result

>>> is_measurement(Omega_coin, A_coin, prob_of_coin_flip)
True

# NGパターン：確率測度を満たさないように関数を作り変えてみる
def prob_of_coin_flip(a: frozenset):
    if a == frozenset(["表"]):
        return 99/100
    elif a == frozenset(["裏"]):
        return 2/100  # <<== 合計が1にならないようにした
    result = 0
    for i in a:
        result += prob_of_coin_flip(frozenset([i]))
    return result

>>> is_measurement(Omega_coin, A_coin, prob_of_coin_flip)
False

ここまで何となく理解できたでしょうか？
可測空間と確率測度、基本的にこの2つが分かっていれば、数学的な意味での確率の考えの土台は理解できていると言っていいのではと思います。

次に取り組むべき山場は、確率変数 と 確率分布 です。
ここまでの話で、確率の概念についてはOKなのですが、実際に関数を使って色々計算したりすることなどを考えると、確率測度は扱いやすいものであってほしいという思いがあります。しかしながら一般の可測空間では、扱いやすい確率測度を作りづらいです。また別の要望として、色々な可測空間ごとに対象の可測空間に閉じた確率測度をその都度作るのではなく、できればどんな可測空間であってもある程度統一的に取り扱えるような確率測度の枠組みがあると嬉しいです。
これをうまいことするために色々工夫するわけですが、その際に重要なキーワードになるのが、確率変数、確率分布、そして ボレル集合族 という特別なシグマ加法族です。

##確率変数
さっきも書きましたが、一般の可測空間上には扱いやすい確率測度を作りづらいです。
例えばさいころ投げなら、 P( { "2の目が出る" } ) = 1/6 みたいな感じで作ることになりますが、入力が事象の関数なんて、実数などとは違って計算もしづらそうだし、色々いじるにしてもやりづらそうです。
もっと計算しやすそうで便利な関数を作れるような都合の良い可測空間の上に議論をすり替えることができたら便利です。

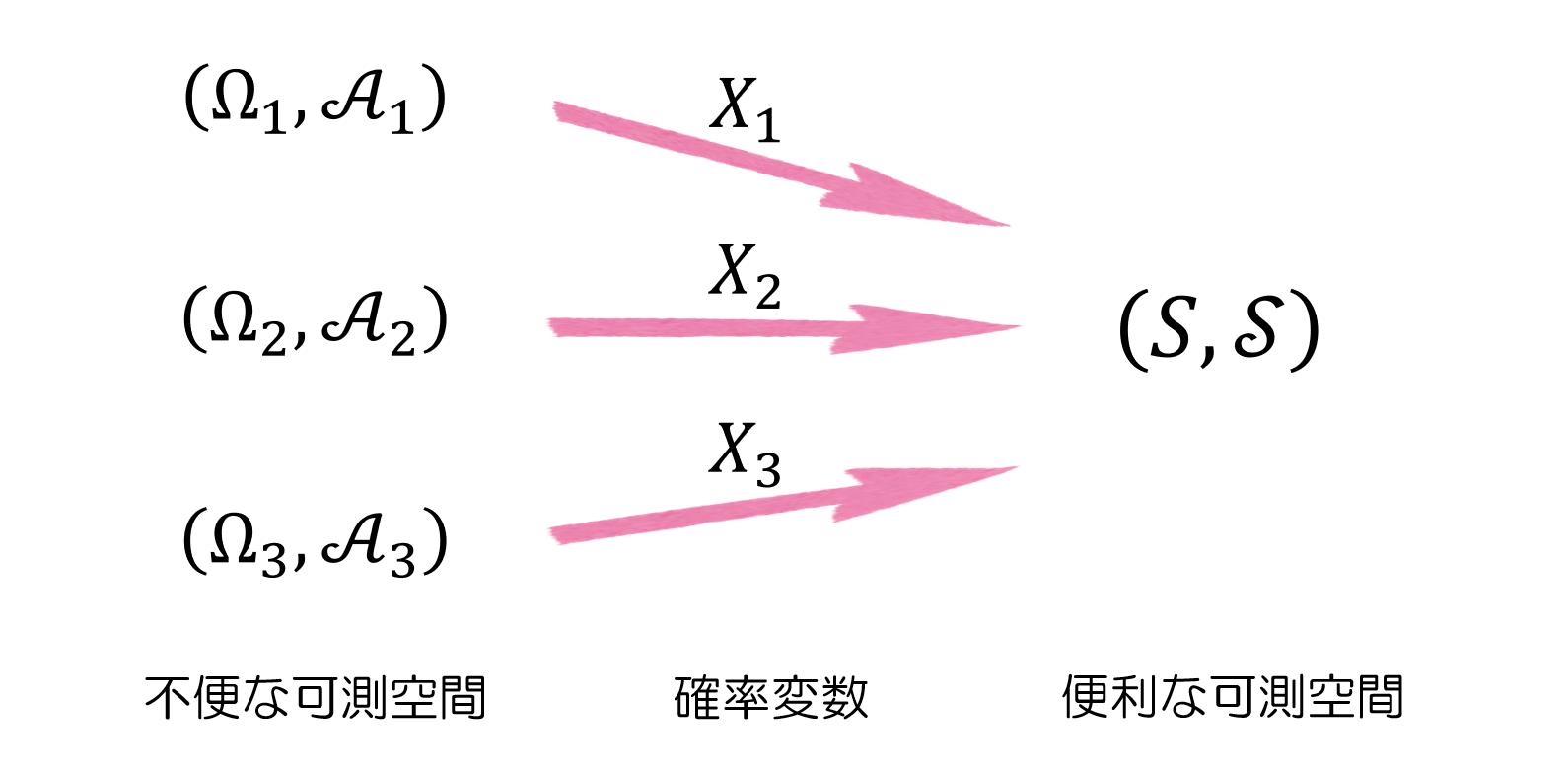
####定義 (確率変数)
$( Ω, \mathscr{A}, P )$ を確率空間とし, $( S, \mathscr{S} )$ は可測空間であるとする。
写像 $ X : Ω \to S $ が次の性質を満たす時、$X$ を $Ω$ 上の $(S, \mathscr{S} )$値確率変数 という。
・任意の $B ∈ \mathscr{S}$ に対して、$X$ の逆像 $X^{-1}(B) = \{ ω ∈ Ω \ | \ X(ω) ∈ B \} $ は $\mathscr{A}$ の要素となる

####確率変数の気持ち
まず注意すべきは、数学用語としての確率変数は写像であるということです。
日常語としての確率変数は、"確率的に値が変わる変数"というやや意味が曖昧な用語でしたが、議論を数学的に整備する際には可測空間の間の写像であると頭を切り替える必要があります。
確率変数 $X$ は、言ってみれば扱いづらい可測空間 $( Ω, \mathscr{A} )$ から扱いやすい可測空間への橋渡し的な役割と言えると思います。
慣れないと見づらいかもしれませんが、上の条件を読み解くと、シグマ加法族 $\mathscr{S}$ の任意の要素は、$X$ を介して $\mathscr{A}$ の要素へと関連付けることができます。つまり、どのような扱いづらい可測空間が与えられてしまったとしても⁹、扱いやすい可測空間 $( S, \mathscr{S} )$ を用意して、そこへの架け橋となるような確率変数 $X$ を作ってあげれば、$( S, \mathscr{S} )$ の世界で得ることができた様々な良い結果を $( Ω, \mathscr{A} )$ の結果として流用できるというわけです。

コード

簡単な例ですが、コイン投げとサイコロ投げでの確率変数を作ってみます。
と言ってもただの if 文ですが。。。というか、確率変数は大抵の場合ただの if 文であるとも言えます。
(確率変数となっていることを確かめるコードも書こうと思いましたが、出来ませんでした。。。)

# コイン投げの例
# 対応する数字は何でも良いですが、表なら0 で裏なら1 として作ります。
Omega_coin = frozenset(["表が出る", "裏が出る"])
def X_coin(w):
    """
    コイン投げにおける確率変数の値を返す
    Args:
        w : Ωの要素

    Returns:
        int
    """
    if w == "表が出る":
        return 0 
    if w == "裏が出る":
        return 1 

>>> X_coin("表が出る")
0

>>> X_coin("裏が出る")
1

# サイコロ投げの例
# 対応する数字は何でも良いですが、ここではサイコロの出目の数値を返すように作ります。
Omega_dise = frozenset(["①", "②", "③", "④", "⑤", "⑥"])
def X_dise(w):
    """
    サイコロ投げにおける確率変数の値を返す
    Args:
        w : Ωの要素

    Returns:
        int
    """
    if w == "①":
        return 1 
    if w == "②":
        return 2 
    if w == "③":
        return 3 
    if w == "④":
        return 4 
    if w == "⑤":
        return 5 
    if w == "⑥":
        return 6 

>>> X_dise("①")
1

>>> X_dise("⑤")
5

さて、では $( S, \mathscr{S} )$ にはどのような可測空間がふさわしいでしょうか？どのような可測空間が、扱いやすい確率測度を作るのに向いているでしょうか？我々は昔から、**実数**の扱いに慣れています。$\mathscr{S}$ の要素は確率測度の入力になるので、もし $\mathscr{S}$ がなにか実数に関わる集合族であれば、扱いやすい確率測度を作りやすそうになるような気がします。

ここでおもむろに、ボレル集合族というものを定義します。

##ボレル集合族
ボレル集合族を定義するには、生成されたシグマ加法族という特別なシグマ加法族の定義を理解する必要があります。
以下に、この2つの定義を同時に提示します。

定義 (生成されたシグマ加法族)

$Ω$ を集合とし、$C$ を $Ω$ の部分集合の族とする¹⁰。

次のように定める $σ(C)$ を、$Ω$ の**$C$ から生成されたシグマ加法族**¹¹という。
$σ(C) := \bigcap_{λ∈Λ} \mathscr{C}_{λ}$

定義 (ボレル集合族¹²)

実数 $a, b ∈ \mathbb{R}$ の開区間 $(a, b) := \{ x ∈ \mathbb{R} \ | \ a < x < b \} $ 全てを集めた集合族
$ \{ (a, b) \ | \ a, b ∈ \mathbb{R}, a < b \} $ から生成される $\mathbb{R}$ のシグマ加法族を ($\mathbb{R}$上の)ボレル集合族といい $\mathcal{B}(\mathbb{R})$ と表記する。

ボレル集合族の気持ち

初見だとかなり混乱をきたすと思います。私もこのボレル集合族を理解するのに苦労しました。
ボレル集合族を構成する動機は、扱いやすい可測空間 $( \mathbb{R}, \mathcal{B}(\mathbb{R}))$を構成したいということだと思えば良いです。確率測度の入力を、事象という扱いづらいものでなく、$\mathbb{R}$ の開区間という扱いやすいものに変換したいという想いが込められている、と私は考えています。
ある部分集合族から生成されたシグマ加法族を定義する動機としては、自分にとって必要な"形"をした集合のみを要素として含むようなシグマ加法族を作りたいという想いがあるのかなと思います。後の節で見ますが、確率測度の入力として $\mathbb{R}$ の開区間を採用できると、積分を活用することで、確率測度を作るのにとても都合が良くなります。
ただ、単に $\mathbb{R}$ の部分集合族となると、その要素となる集合の"形"は非常に様々です。様々あり過ぎて、確率測度の入力として使う為にはあまり複雑でワイルドな部分集合は含まれていて欲しくないのです。
今欲しいのは、目的の"形"をした集合(今で言うと $\mathbb{R}$ の開区間)と、シグマ加法族の3つの条件を満たす為に必要になる最低限の集合だけを含むようなシグマ加法族です。それを作る為に、まず $\mathbb{R}$ の開区間を含む任意のシグマ加法族("ゴミ"が含まれていても良い)を全て集めてきて、それら全ての共通部分をとることで不必要な要素を除去しています。
結果として、$\mathcal{B}(\mathbb{R}) )$ に含まれるのは、例えば ( 0, 1 ) とか ( -10, 1/2 ) といった開区間と、それらの補集合及び高々加算個の合併になります。
このようにして作ったシグマ加法族をボレル集合族といい、可測空間 $( \mathbb{R}, \mathcal{B}(\mathbb{R}) )$ を先ほどの確率変数の橋渡し先として用意するわけです。

コード

ボレル集合族をコードで表現するのは私の腕では難しいので、生成されたシグマ加法族を作るコードを書いてみます。
きっともっとうまくやる方法があるのでしょうが、諸般の事情により$Ω$ の全ての部分集合を列挙して、そこから全ての部分集合族を列挙して、その中でシグマ加法族になるものを抽出して、最後に共通部分をとるという力技でやってます。
($Ω$ の要素数が5つ以上で真似すると恐らく止まりますのでご注意ください)


# Ω を3つの要素を持つ集合とする
>>> Omega = frozenset({ "a", "b", "c"})

# Ωの部分集合を全部リストにする
>>> subset_list = []
>>> for i in range(2**len(Omega)):
        elements = list(Omega)
        subset = frozenset()
        flag = format(i, "0{0}b".format(str(len(Omega))))
        for j in range(len(Omega)):
            if flag[j] == "1":
                subset = subset.union(frozenset(elements[j]))
        subset_list.append(subset)


# Ωの部分集合族を全部リストにする (要素数は2^2^{Ωの要素数}になる)
>>> set_families = []
>>> for i in range(2**len(subset_list)):
        set_family = []
        flag = format(i, "0{0}b".format(str(len(subset_list))))
        for j in range(len(subset_list)):
            if flag[j] == "1":
                set_family.append(subset_list[j])
        set_family = frozenset(set_family)
        set_families.append(set_family)


# Ωの部分集合族のうちシグマ加法族の条件を満たすものだけを抽出してリストにする
>>> sigma_algebra_list = []
>>> for set_family in set_families:
        if has_sigma_additivity(Omega, set_family) == False:
            pass
        else:
            sigma_algebra_list.append(set_family)


# 生成されたシグマ加法族を作る
# 生成元の部分集合族 C を適当に作る
>>> C = frozenset([frozenset(["a"]), frozenset(["c"])])

# Cから生成されたシグマ加法族を作る
>>> sigma_algebra_gen_C = frozenset({frozenset(),
            frozenset({'c'}),
            frozenset({'b'}),
            frozenset({'b', 'c'}),
            frozenset({'a'}),
            frozenset({'a', 'b'}),
            frozenset({'a', 'c'}),
            frozenset({'a', 'b', 'c'})}) # Ωのべき集合を初期値にしている

>>> for sigma_algebra in sigma_algebra_list:
        if C.issubset(sigma_algebra) == True:
            sigma_algebra_gen_C = sigma_algebra_gen_C.intersection(sigma_algebra)


# 確認
>>> sigma_algebra_gen_C
frozenset({frozenset(),
           frozenset({'c'}),
           frozenset({'a'}),
           frozenset({'a', 'c'}),
           frozenset({'a', 'b', 'c'})})

舞台はかなり整ってきました。
あとは、元の可測空間 $( Ω, \mathscr{A} )$ 上の確率測度 $P$ に紐付く形で、$( \mathbb{R}, \mathcal{B}(\mathbb{R}) )$ 上に新たな確率測度を定義すれば全てが繋がります。
ここで確率分布が出てきます。

##確率分布
####定義 (確率分布)
可測空間 $( \mathbb{R}, \mathcal{B}(\mathbb{R}) )$ 上に確率測度 $P_{X} : \mathcal{B}(\mathbb{R}) \to \mathbb{R}$ を次のように定める。
$ P_{X}(B) = P( X^{-1}(B))　　( B ∈ \mathcal{B}(\mathbb{R}) ) $
このようにして定めた確率測度 $P_{X}$ を、確率変数 $X$ によって定まる確率分布という¹³

確率分布の気持ち

登場人物がひととおり出揃いました。
確率分布とは、数学的には $( \mathbb{R}, \mathcal{B}(\mathbb{R}) )$ 上の確率測度なのです。
日常語としての確率分布とは少々イメージが違ったかもしれませんが、よーく読むと整合性を損なわずに上の定義としての文脈で表現できるはずです。
確率分布は確率測度なので、もちろん一般的には(確率測度の条件さえ満たせば)様々な形を取り得ますが、入力が $\mathbb{R}$ の開区間¹⁴なので、積分や総和を使えば扱いやすい良い感じの関数が表現できそうな気がします。
なので、多くの場面で確率分布は次のような形をした関数として表現されるかと思います。

$$
P_{X}((a,b)) = \int_{a}^{b} f(x) dx
$$
$$
P_{X}((a,b)) = \sum_{x ∈ (a, b) } f(x)
$$

そして、上式における $f(x)$ を確率密度関数とか、確率質量関数と呼んでいるのでした。
例えば、正規分布 $N( μ, σ^{2} )$ に従う確率分布とは、この確率密度関数が

$$
f(x) = \frac{1}{\sqrt{2\pi σ^{2}}} \exp\biggl(-\frac{(x-μ)^{2}}{2σ^{2}}\biggr)
$$

という形をした $( \mathbb{R}, \mathcal{B}(\mathbb{R}) )$ 上の確率測度のことを言うというわけです。

そして、思うに、確率分布の良いところは、元の可測関数 $( Ω , \mathscr{A} )$ からは確率変数 $X$ で $( \mathbb{R}, \mathcal{B}(\mathbb{R}) )$ に議論を引きずり込んできているので、実用の際には $( Ω , \mathscr{A} )$ 上の確率測度 $P$ をいちいち考えることなく、$( \mathbb{R}, \mathcal{B}(\mathbb{R}) )$ 上の確率分布を考えれば良いということだと思います。つまり、あたかも元の確率空間のことを"忘れた"かのようにことができるのが大きな利点ではないかなと思います。

ここまでの話で私の書きたかったことは一応書いたのですが、抽象的な話が多かったので、練習のため正規分布を具体例としてここまでの話を使って書き下してみたいと思います。

##具体例:正規分布に従う確率変数とは
題材として、"日本人成人男性の身長の分布" を選ぶことにします。

まず、これまでに出てきた記号を具体的に書いていきます。
可測空間 $(Ω , \mathscr{A} )$ :
$Ω = $ {日本人成人男性の全体}
$\mathscr{A} = 2^{Ω}$　($Ω$ の冪集合)
確率測度 $P$ については今は考えません。

確率変数 $X : Ω \to \mathbb{R}$ :
$ω ∈ Ω$ に対して、$X(ω) =$ "身長の大きさ"　とします。
例えば、私の身長は約170cmなので、X( "私" ) = 170.xx… のようになります。
(小数点以下はわかりませんが無限に続くはずです。)

これが確率変数になるのは $\mathscr{A} = 2^{Ω}$ を冪集合としているのでほぼ明らかですが、例えば $( 165 , 170) ∈ \mathcal{B}(\mathbb{R})$ でチェックすると、 $X$ の逆像は、
$X^{-1}( (165 , 170) ) = \{ ω ∈ Ω \ | \ X(ω) ∈ (165 , 170) \}$
となり、$ω$ は身長が165cmより大きく170cmより小さい人となるので、そのような $ω$ 全体を集めた集合は $\mathscr{A}$ の要素となるのでOKです。

ここで、次のような仮定を置きます。
仮定:日本人成人男性の身長の分布は、平均170cm, 分散36の正規分布に従うとする¹⁵

この時の確率分布 $P_{X} : \mathcal{B}(\mathbb{R}) \to \mathbb{R}$ は、先ほどの確率密度関数において $μ = 170, σ^{2} = 36$ と置いて、
$$
P_{X}((a,b)) = \int_{a}^{b} \frac{1}{\sqrt{2\pi36}} \exp\biggl(-\frac{(x-170)^{2}}{236}\biggr) dx
$$
のようになります。
例えば、"自分の子供が将来身長180cm以上になる確率" (または、任意に抽出した1人の身長が180cm以上である確率)というのは、よく $Pr( 180 ≦ X )$ などのように、あたかも $X$ が関数の入力変数のような表記がされますが、これは暗黙のうちに上のような確率変数を利用していて、単に $P_{X}((180, \infty))$ を計算すれば良いというふうに解釈できます。つまり、
$$
P_{X}((180, \infty)) = \int_{180}^{\infty} \frac{1}{\sqrt{2\pi 36}} \exp\biggl(-\frac{(x-170)^{2}}{236}\biggr) dx ≒ 0.04779 ≒ 4.8 \%
$$
のように計算することで確率が求まります。¹⁶

ところで、元の可測空間 $( Ω , \mathscr{A} )$ の確率測度を決めていなかったですが、多くの場合ではそれを決めずに直接 $P_{X}$ を決めて問題ないのだと思います。
本来的には、"身長が○○cmより大きく○○cmより小さい人" を $Ω$ から取ってきて、その人達を集めた $Ω$ の部分集合の全てに対して出力を決めるような確率測度 $P$ を定義し、その $P$ を元に $X$ から誘導される $P_{X}$ を決めるのですが、そのような $P$ を書き下すのはなかなか大変です。初めから何らかの分布に従うと仮定することを見越していれば、確率分布の定義から
$P_{X}( (a,b) ) = P(X^{-1}( (a, b) )) = P( \{ ω ∈ Ω \ | \ X(Ω) ∈ (a, b) \} )$
なので、$P_{X}$ 上の確率分布を決めてしまえば $\mathscr{A}$ 上の確率測度はそこから引き戻して考えると自然に決まるので、あまり $P$ を先に書き下すことはせずに暗黙のうちに決まっていると前提している場合が多いと思います。

さいごに

いかがだったでしょうか？
異様に長くなってしまいましたが、ここまで読んでくれた方、誠にありがとうございます。
本当は、同時分布とベイズの定理をこの文脈で書き下すこともしようと思っていたのですが、途中で挫折してしまいました。。。いつかまた続編で書ければなと思います。

ともあれ、これで私としては今後確率の話の中で頭が混乱することがあっても、落ち着いて頭の中でこれまでの内容を展開することで、納得感を持って読み進められる気がしています。
これが皆様の確率・統計の学習の一助にもなれば幸いです。

逆に、そもそもモヤモヤを感じずに読み進めていけるよという人は不要かもしれません(いたずらに混乱をきたすかもしれません) ↩
$\mathscr{A}$ の呼び名は書籍によって様々で、他にも完全加法族やシグマ代数などという表記も見かけます。本文ではシグマ加法族で統一します。ちなみにシグマ加法族によく使われる記号 $\mathscr{A}$ はドイツ文字のAで、フォントは花文字フォントというそうです。他にも $\mathscr{F}$ という記号が使われたりします。 ↩
この段階ではまだ確率測度が出てきていないので一般の測度論の話なのですが、ここでは確率論をベースとして気持ちを書きます ↩
要素が1つだけの集合をシングルトンと呼びます ↩
私の知る限りたぶんないです ↩
思いませんかね？？私はとても思いました...... ↩
確率変数、確率分布という言葉を先に出してしまいましたが、ここはフワッと読んでください
確率論を使うのはその後です。そのようにして、確率論から曖昧さやランダム性を排除しています。 ↩
その判断の確からしさの指標をモデルするような理論もあるようですが、最終的に判断を人間に委ねるという意味では結局は同じことだと思います(詳しくないのでよくわかりませんが...) ↩
"どのような" はかなり強い表現ですが、実際の場面ではほぼこの認識でいいだろうと思います。
また、定義式の$( S, \mathscr{S} )$ に利用するものを、汎用的に使える良い可測空間に絞って考えることで、流用の効率を上げることができるという実用上のメリットがあると思います。元の可測空間がどのようなものでも、$X$ をうまく与えさえすれば、同一の可測空間 $( S, \mathscr{S} )$ と紐付けることができます。 ↩
念のためですが、$C$ はシグマ加法族とは限らない、一般の部分集合族です
また、$Ω$ のシグマ加法族で、$C$ を含むようなもの全体を $\{ \mathscr{C_{λ}} \}_{λ∈Λ}$ ( $Λ$ は添字の集合) とする。 ↩
このようにして作った $σ(C)$ が $Ω$ のシグマ加法族になることは証明を必要としますが、今回は読者の演習問題とします。。。 ↩
今回は対象を $\mathbb{R}$ 上のボレル集合族に絞った定義とします。本当はボレル集合族はもっと広い集合を対象に定義されますが、確率論で使われるのはほぼ $\mathbb{R}$ (または $\mathbb{R^n}$)上のボレル集合族がほとんどだと思いますので、話がややこしくなるのでこのようにします。 ↩
このようにして定めた $P_{X}$ が確率測度の条件を満たすということは証明が必要ですが、これも読者の演習問題とします。 ↩
正しくは開区間だけとは全然限らないのですが、実用では多くの場合が開区間での確率の話になるかと思います。次の行の式も、本来は入力は $A ∈ \mathcal{B}(\mathbb{R})$ に対して、右辺は $A$ 上のルベーグ積分になりようですが、話がいたずらに発散する気がするので開区間に限った書き方をしています。 ↩
平均、分散の値は適当ですので実際のデータとは違うかもしれません。
この、正規分布に従うという仮定は本当に正しいかどうかわかりませんが、経験上そのように信じられるので、そのように仮定するわけです。 ↩
具体的な計算自体は Wolfram Alpha 先生にお願いしました。 ↩

175

161

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up