序
突然, "あなた"が何かしらのデータをもらったとしましょう.
そして**「なんか機械学習ってやつを使って面白いことやって」**と言われてしまったらどうしますか.
苦心して色んなアルゴリズムだとかプログラムだとかを調べて予測モデルみたいなものを作るもよし, あるいは大仰な機械学習なんてものを実は必要としていないと看破できれば, 統計学的なデータ分析をしてみてもいいでしょう.
( たぶん正解は**「そんなこと言ってくる人とは関わらないようにする」**ですが. )
ここではそんなことを言われてしまった哀れな"あなた"に**「関係性のモデリング」**という観点から, グラフィカルモデルというものを通した統計的・機械学習的モデリング( ひいては数理モデリング )を大体イチから( $\iff$ 数理的な側面をきっちりと踏まえて )お伝えしていこうと思います.
間違っている, あるいは間違っている「気がする」記述を発見された方はコメントにて即座にお伝えいただければ幸いです. ネットという公開された海に誤っている情報が載っているのは不幸な人を増やすだけなので・・・
ちなみに今回お伝えする手法はどちらかといえば統計学のドメインに近いお話です. しかし, 「なんか面白いことやって」とデータ大喜利を要求してくる人は手法が機械学習のドメインに属するか統計学のドメインに属するかなんて分かるわけがないので今回は気にしないことにします.
この記事を読むとこんなものができる
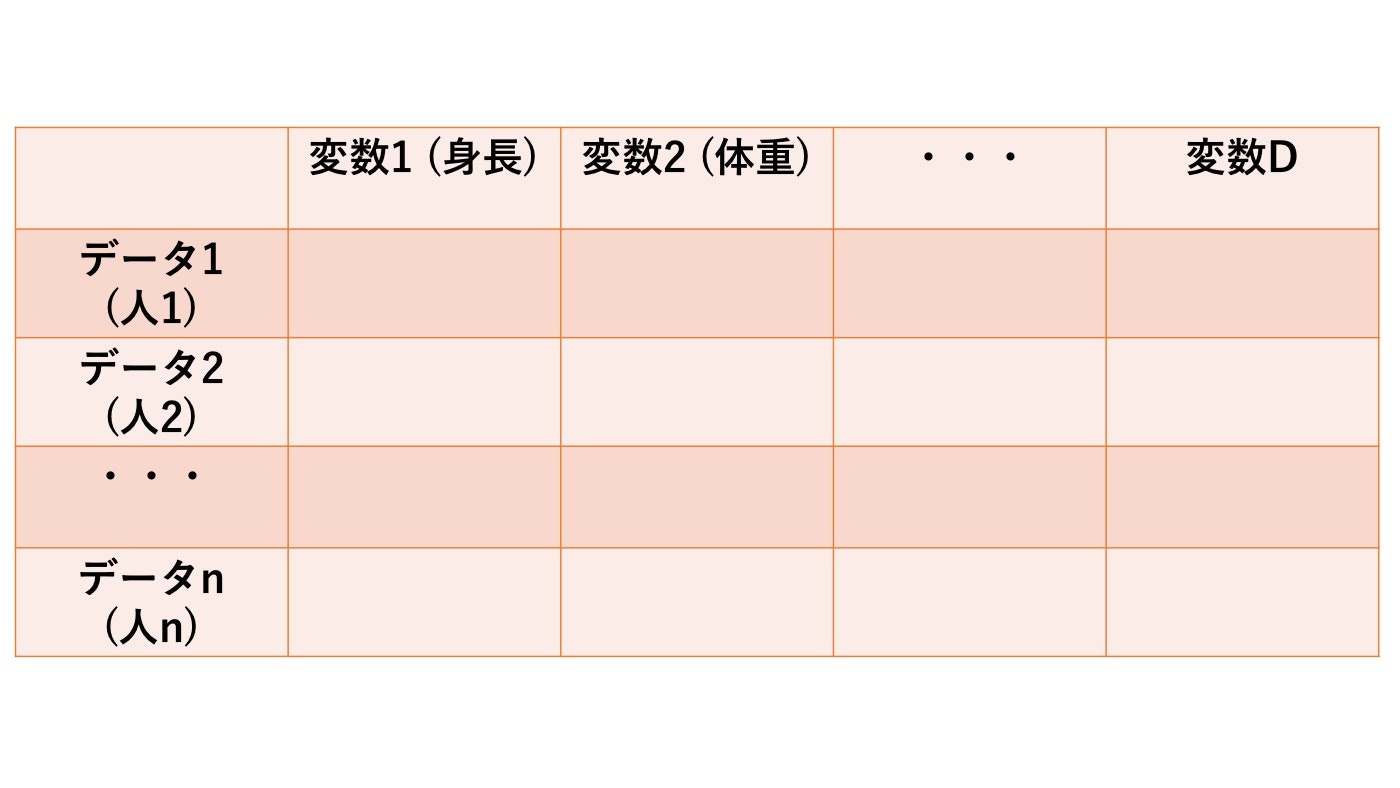
例えばデータがこんな形で与えられているとします.
このとき, 変数$1$から$D$までの関係をデータから学習して次のように可視化することができるようになります. ( この図だと$D$=10 )
この記事では数理的にはどうモデリングできるか?ということをいちいち考えていくので, **そういった細かいことはどうでもいいよ!**という人はGraphical Lassoの節から読むことをお勧めします.
データは揺らぐ。
ぼーっとデータを眺めていた"あなた"はあることに気づきました. データの一つの列を見ていくと値一つ一つは何となく一つの値の周りでバラついているような気がします. ( もしかしたら気のせいかもしれないけど )
$$ 3.0, 3.5, 3.2, 3.6, \dots$$
そもそもこういったバラバラする量はどうやって表現すれば良いのでしょうか?もし数理的に表現することができれば定量的に論じることができますし, 行ってよい操作が論理的にわかります.
数理的にはこのようなバラつく値を確率変数というものを使って表現します. ( なお, 今回は確率変数として$\mathbb{R}$上のもののみを考えることにします. )
確率空間を$(\Omega, \mathcal{F}, P)$とする. $\Omega$上の実数値関数$X: \Omega \to \mathbb{R}$が確率変数であるとは, 任意の$A \in \mathcal{B}(\mathbb{R})$に対し, $A$の$X$による逆像
$$ X^{-1}(A) := \{ \omega \in \Omega \ | \ X(\omega) \in A \}$$
が$X^{-1}(A) \in \mathcal{F}$を満たすことである. なおここで, $\mathcal{B}(\mathbb{R})$とは$\mathbb{R}$上のボレル集合族を表す.
定義だけを書いてしまうと何が何だか直観的にははっきりしませんが, これは「観測した結果$A$」が起こる確率を計算できること, という定義になっています. しかも面白いことに, 「どれくらいバラバラするか」ということを, $A$が起きたとき, データ$A$の背後にあるっぽい標本$\omega$の数を数える( 確率測度を計算する )という風に, データが発生する方向( $\omega \to x$ )とは逆に辿る( $x \to \omega$ )ことで表現しています.
さて, このようにデータを確率変数として捉えることでデータの取り扱いを数理的なフィールドにとりあえず持ってくることができました.
しかし, これだけではデータに関して何を述べていいのやら全くわかりません. モデリングしたけどこれの何が嬉しいの?となってしまいます.
一番いいのはデータが発生する法則がわかればいいですよね. そうすればデータに関してわかった顔ができます.
数理的に確率変数の法則は確率分布として表現できます.「え, 確率分布?それはさすがに聞いたことあるよ」という方も多いかとは思いますが, 実際に分布とは何か説明できるでしょうか?多分意外と難しいと思います.
確率空間を$(\Omega, \mathcal{F}, P)$とし, $\Omega$上の実数値確率変数$X$を考える. このとき, $X$の確率分布とは$A \in \mathcal{B}(\mathbb{R})$に対し,
$$ P^{X}(A):= P(\{ \omega \ | \ X(\omega) \in A \})$$
という確率測度によって誘導される($\mathbb{R}, \mathcal{B}(\mathbb{R})$)上の確率測度のことを言う. 特に$P^X$が$(\mathbb{R}, \mathcal{B}(\mathbb{R}))$上のある確率測度$Q$に等しいとき, $X$は確率分布$Q$に従う, という.
よく「〇〇分布に従う」などの表現が出てくると思いますが, 定義としてこうなっている, ということを整理しておくのは大事なんじゃないかなあと思っています.
ちなみになぜ分布が法則と言えるかと言うと, この分布というものがわかっているとデータ$X$について知りたいこと( 例えば, 「$X$が3より大きくて5より小さくなること」 )が起きる確率を, よく知られた確率の計算方法$Q$で計算できるようになるからです.
今, データは一つの決定的な法則( 例えば「ずっと3になるよ!」など )に残念ながら従っていなさそうなので, ちょっと妥協した上でどこまで言えるかを考えてみて, 「データの振る舞いについての確率がよく知っている形でわかる」, という風に緩めているとも見れそうですね.
なお, ここで定義した確率変数や確率分布といった概念はベクトルの場合にも拡張できます. ここではその拡張を認めた上で先へ進むことにします.
実は確率分布は, 次のようなもう少し取り扱いやすい形にまで表現を変えることができます.
$\mathbb{R}^D$ 上の確率測度$Q$に対して, ある非負ボレル可測関数$p: \mathbb{R}^D \to \mathbb{R}_{>0}$が存在して, $A \in \mathcal{B}(\mathbb{R}^D)$に対し,
$$
Q(A) = \int_A p(x) dx
$$
となるとき, $p$を$Q$の確率密度関数といい, $Q$は絶対連続分布であるという.
これの言っていることはデータ$X$の法則$Q$がある程度"いい感じ"なら$p(x)$を法則と見てみてもいいですよ, ということです. ( もちろんそれだけではないですが. ) この表現はよく使われる表現で, この$p(x)$を取り替えて遊ぶところから統計の入門編はスタートしていることが多いと思います. $p(x)$として正規分布の確率密度関数を考えたり, 指数分布の確率密度関数を考えたり・・・という感じで.
さて, 少し固めの表現とはなってしまいましたが, データを数理的に取り扱い, データから導きたい法則についても数理的にモデリングすることが出来ました.
しかし, まだまだ捉えきれていない概念があります.
「関係」とは?
ものごとの「関係」って何でしょう?
これは非常に抽象的な問いですが, 数理的な関係性の表現の一つとして「直接関係がない」とは**「確率変数が条件付き独立である」**と言えます.
関係性(条件付き独立)を数理的にモデリングしたいのですが, そのためには条件付き確率密度関数というものが必要となるので, まずはそちらについてお伝えします.
確率変数$X, Y$の同時確率密度関数$p(x, y)$が存在する時, $p(y) = \int p(x, y) dx$とし, $X$を$Y$で条件付けた条件付き確率密度関数$p(x \ | \ y)$を,
$$
p(x \ | \ y) = \begin{cases}
\frac{p(x, y)}{p(y)} & (p(y) \ne 0)\
0 & (p(y) = 0)
\end{cases}
$$
で定義する.
さて, これで確率密度関数がある場合の条件付き独立性について述べることができます.
確率変数$X, Y, Z$に対し, 同時確率密度関数$p(x, y, z)$が存在した時, $X$と$Y$が$Z$を条件付けた下で独立であるとは,
$$
p(x, y \ | \ z) = p(x \ | \ z) p(y \ | \ z)
$$
となることである. これは
$$
p(x, y, z) = f(x, z) g(y, z)
$$
なる関数$f(x, z), g(y, z)$が存在することと同値である.
定義が何やら並んでいますが, $x_i$と$x_j$の条件付き独立性とは他の変数$x_1, \dots, x_n$を統制した時に$x_i$と$x_j$が無関係になるかどうかをみている, ということになります. 他の条件を整えた上で, 二つの変数だけに注目しているということなので, これはいわば$x_i$と$x_j$について実験している, というようなことに対応しています. そのため相関関係なんかよりも基本的にはずっと強いことを言っていることになります. ( ただし, 条件付き独立性は独立性の必要条件でも十分条件でもありません. )
この条件付き独立性を元にして組み立てられたモデリングの方法が「グラフィカルモデル」と呼ばれるモデリング手法です.
グラフィカルモデルの中には「ベイジアンネットワーク」だとか「因子グラフ」などといったものがあるんですが, 今回はその中でも, 関係性を無向グラフで表現する「マルコフ確率場」( マルコフネットワーク )というものを紹介していきます.
マルコフ確率場
単刀直入に定義から。
グラフ$G = (V , E)$の各頂点$v \in V$に確率変数$X_v$が対応付けられているとする. この時, $uv \not \in E$である任意の$v, u \in V$に対し, $X_{V - \{v, u\}}$を条件付けた上で$X_v$と$X_u$が条件付き独立になるなら, $(X_v)_{v \in V}$をマルコフ確率場という.
グラフの頂点一つ一つに確率変数をぺたぺたと貼っていって, 「関係」があれば線で点二つを繋ぐ, そうでなければ繋がない, ということを単純に行ってください, というのが上の「関係性」のグラフ化であるマルコフ確率場の定義です.
本当はもう少し強い定義をするのですが, 今回の状況設定ではこれで十分なモデリングとなっています.
このようなモデリングをすることによって変数間の関係という「ふわふわした」問題が, グラフに対応する確率変数の条件付き独立性という数理的な枠組みで語ることができるようになりました.
ここまで出来れば"あなた"はモデリングの第一段階はクリアできたといっていいでしょう.
データの「法則」を仮定する
上の方でマルコフ確率場なんてものが出てきましたが, 実はこれ, 一般的な確率変数の集合に対して計算するのは非常に難しいです. 積分が解析的に実行できない, 計算量的に手に負えないなどの理由で, 抽象的に語るのは困難な問題です.
そのためここでは大胆に**「データが従う分布は正規分布である」**と仮定することにします. これによって表現力はもちろん小さくなってしまうんですが, 計算を一般の場合に比べてはるかに高速に行うことができます.
ここで正規分布の確率密度関数について見てみましょう.
$x$を$x \in \mathbb{R}^D$なる確率変数ベクトル, 平均ベクトル$\mu \in \mathbb{R}^D$, 精度行列( 分散共分散行列の逆行列 ) $\Lambda \in \mathbb{R}^{D \times D}$ ( 正定値対称 ) として, $x$が多変量正規分布に従うとき, その確率密度関数は
$$p(x ; \mu, \Lambda) = \frac{\sqrt{\det \Lambda}}{\left(\sqrt{2 \pi}\right)^D} \exp \left\{ - \frac{(x - \mu)^T \Lambda (x - \mu)}{2} \right\}$$
と書くことができる.
見慣れている人にとっては見慣れているこの式ですが, 「条件付き独立」という眼鏡を通してみてみると大変喜ばしい性質を持っていることがわかります. ここで$V$を$x_1, \dots, x_D$と対応づけることにします. つまり, $|V| = D$ですね. このとき, $x_i$と$x_j$に注目して, 条件付き確率密度$p(x_i, x_j \ | \ x_{V - \{i, j\}})$を考えてみると,
$$
\begin{align}
p(x_i, x_j \ | \ x_{V - \{i, j\}}) &\propto \exp \left\{- \frac{1}{2} \left( \Lambda_{ii} x_i^2 + 2 \Lambda_{ij} x_i x_j + \Lambda_{jj} x_j^2 \right) + A x_i + B x_j + C\right\}
\end{align}
$$
となります. このとき$\Lambda_{ij} = 0$なら二つの関数の積$f(x, z)g(y, z)$となることなどに注意すれば
$$
\Lambda_{ij} = 0 \iff x_i と x_j が条件付き独立
$$
が成立します. すなわちマルコフ確率場を考えるには精度行列$\Lambda$がわかりさえすれば良い, ということがわかります. この性質のため, データが正規分布に従う, という思い込みの下ではマルコフ確率場の構成はとても速くなります.
データからパラメータを推定する
前節にてデータが正規分布に従っていると思った時にマルコフ確率場が計算しやすくなることがわかりましたが, では"あなた"が実際にデータから精度行列$\Lambda$を推定するにはどうすれば良いのでしょうか?
この推定の仕方にはMAP推定やベイズ推定などの枠組みがありますが, ここでは最も原始的な最尤推定という枠組みを考えることにします.
次のように定義される尤度と呼ばれるものを考えてみましょう.
データを$X := \{x_1, \dots, x_n\}$と書くことにし, $x_1, \dots, x_n \sim \mathcal{N}(\mu, \Lambda)$である( 一つ一つのデータが多変量正規分布に従う )と仮定します. また各データは独立に得られると仮定します. すると, 尤度$L(\mu, \Lambda)$は
$$
L(\mu, \Lambda) = \prod_{i=1}^{n} p(x_i; \mu, \Lambda)
$$
と表されます. この量は今のデータが起こる"確率"を大体表しているものと解釈できます. これをできるだけ大きくするようなパラメータ$\mu, \Lambda$を求めに行こうという考え方を最尤推定と言います.
尤度の最大化にはよく$\log$( $\log$は単調な関数であることに注意 )をとったものが考えられ, それを対数尤度と呼びます. 対数の方が$\prod$ではなく$\sum$で計算をすることができるのでアンダーフローを起こしにくく, 数値的に安定ということも言えます. というわけで対数尤度を最大にする$\mu, \Lambda$を求めることにします. 今, 対数尤度を$l(\mu, \Lambda)$とおくと
$$
\begin{align}
l(\mu, \Lambda) &:= \log L(\mu, \Lambda)\
&= \sum_{i=1}^{n} \log p(x_i ; \mu, \Lambda)\
&= - \frac{n D}{2} \log 2 \pi + \frac{n}{2} \log \det \Lambda - \frac{1}{2} \mathrm{tr} \left( \Lambda \sum_{i=1}^n (x_i - \mu) (x_i - \mu)^T \right)\
&= - \frac{n D}{2} \log 2 \pi + \frac{n}{2} \log \det \Lambda - \frac{n}{2} \mathrm{tr} \left( \Lambda S \right)
\end{align}
$$
となります. ここで, $S$は標本分散共分散行列
$$
S = \frac{1}{n} \sum_{i=1}^n (x_i - \mu) (x_i - \mu)^T
$$
です. まず$\mu$について偏微分すると
$$
\begin{align}
\frac{\partial l}{\partial \mu} &= - \frac{1}{2} \sum_{i=1}^n \Lambda (\mu - x_i)
\end{align}
$$
となり, $\Lambda$が正則なことに注意してこれを$0$とおくと
$$
\mu_{\mathrm{MLE}} = \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i
$$
と計算できます.
次に$\Lambda$について$l(\mu, \Lambda)$を偏微分すると
$$
\begin{align}
\frac{\partial l}{\partial \Lambda} &= \frac{n}{2} \Lambda^{-1} - \frac{n}{2} S
\end{align}
$$
となり, $\Lambda^{-1} = \Sigma$と書いて, 上式を$O$とおくと
$$
\Lambda_{\mathrm{MLE}} = \Sigma_{MLE}^{-1} = S^{-1}
$$
を得ます.
じゃあちょっとやってみましょう
精度行列$\Lambda$が次で表されるような正規分布に従うデータを1000個用意して, $\Lambda_{\mathrm{MLE}}$を計算してみることにします( 実装はGitHubにあげておきます こちらから )
[[1.18. -0.43 0. 0. 0. 0. 0. ]
[-0.43 1.51 0. -0.71 0. 0. 0. ]
[0. 0. 1. 0. 0. 0. 0. ]
[0. -0.71 0. 1. 0. 0. 0. ]
[0. 0. 0. 0. 1. 0. 0. ]
[0. 0. 0. 0. 0. 1. 0. ]
[0. 0. 0. 0. 0. 0. 1. ]]
最尤推定で求めた精度行列がこちら
[[ 1.1 , -0.39, -0.02, -0.03, 0.02, -0.03, 0.01],
[-0.39, 1.48, -0.05, -0.7 , -0.02, -0. , -0.04],
[-0.02, -0.05, 1.03, 0.06, 0.02, 0.02, 0.08],
[-0.03, -0.7 , 0.06, 1.01, -0.03, -0.02, 0.03],
[ 0.02, -0.02, 0.02, -0.03, 1.01, 0.01, 0.04],
[-0.03, -0. , 0.02, -0.02, 0.01, 0.98, -0.04],
[ 0.01, -0.04, 0.08, 0.03, 0.04, -0.04, 1.04]]
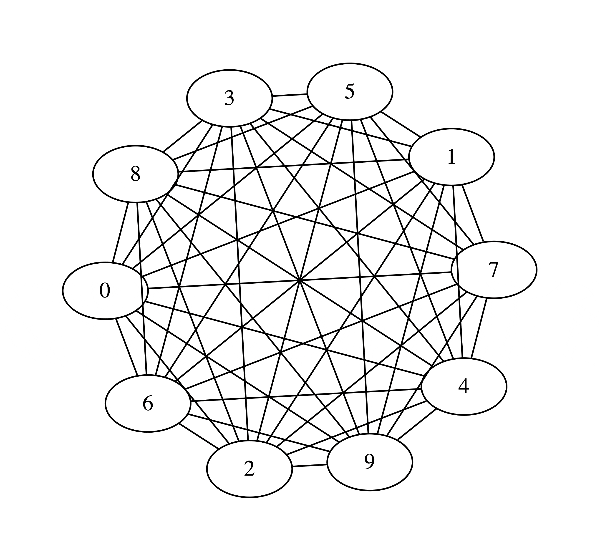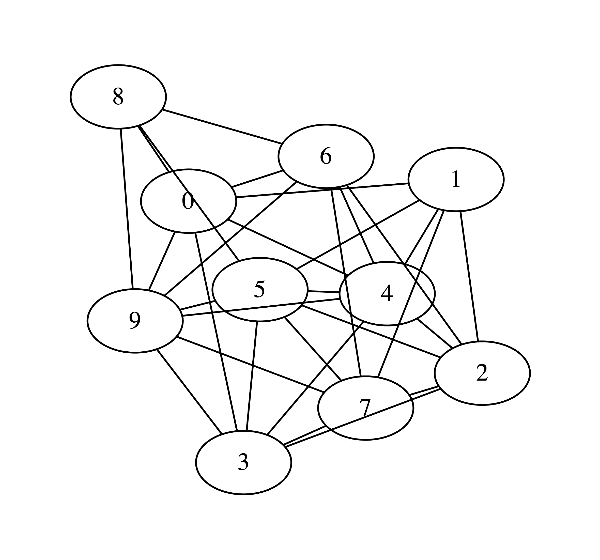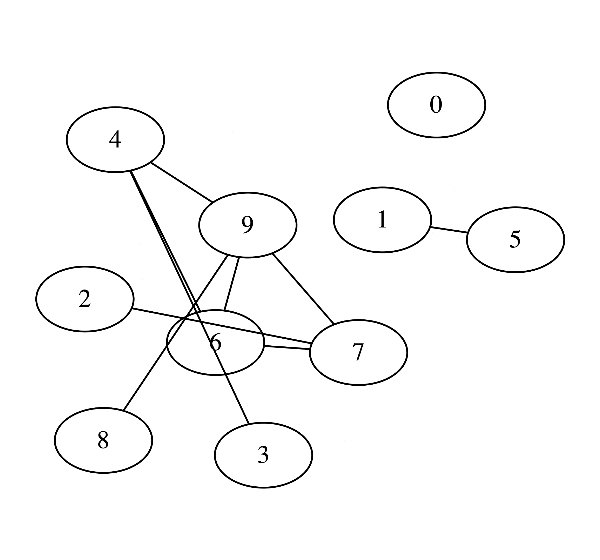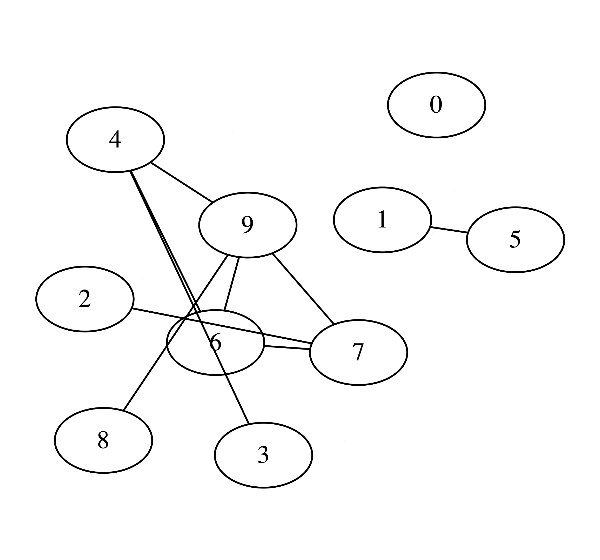
だいぶ近い値を取っていそうですが, グラフィカルモデルとしてはこうなってしまいます.

本当はあまり枝がないのに推定されたグラフは完全グラフとなってしまっていますね. 「枝がそんなにないマルコフ確率場の推定」という観点で考えた時, そのまま最尤推定するのは筋が悪そうです.
Graphical Lasso
割と枝がない( スパースな )マルコフ確率場を推定するためにはどうすればいいでしょう? 統計・機械学習の分野においてこういったスパースな解を求めたい, という問題は正則化によって対処されることがあります. 今回の場合, 精度行列に対する正則化を加えた最適化問題は次のように定式化されます.
$$
\begin{cases}
\max_{\Lambda} & l( \mu = \bar{x}, \Lambda ) - \rho ||\Lambda||_{1}\
s.t. & \Lambda \succ O
\end{cases}
$$
対数尤度を大きくしたいんだけど, $\Lambda$の非ゼロ成分が多いと何らかの罰を加えたいといった気持ちです.
これを解くための高速なアルゴリズムが題にあるGraphical Lassoです.
Graphical Lassoを使って精度行列を推定してみると, 次のようになります. ($\rho = 0.1$で決め打った場合 )
[[ 1.03, -0.28, -0. , -0.02, 0. , -0. , 0. ],
[-0.28, 1.26, -0. , -0.55, -0. , -0. , -0. ],
[-0. , -0. , 1.02, 0. , 0. , 0. , 0. ],
[-0.02, -0.55, 0. , 0.88, -0. , -0. , 0. ],
[ 0. , -0. , 0. , -0. , 1.01, 0. , 0. ],
[-0. , -0. , 0. , -0. , 0. , 0.98, -0. ],
[ 0. , -0. , 0. , 0. , 0. , -0. , 1.03]]
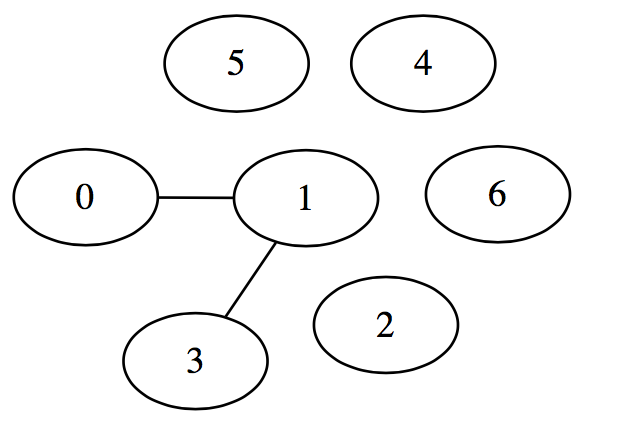
かなり0の成分が多くなっていることがわかりますね. 実際対応するグラフィカルモデルを書いてみると

という風にかなりいい感じに元のデータのグラフィカルモデルを推定できていることがわかります.
$\rho$の値は対数尤度をスコアとしたCVなどでデータから決めることができます.
Graphical Lassoを実データに使う際の注意
- 正規分布という仮定はかなり強いです.
- 単峰性です. (お山が一つ)
- 裾は$\exp$オーダーで減っていきます. ( コーシー分布とかはダメ )
- 対称性があります.
- 整数値だけをとるということはありません.
- そもそもデータが$i.i.d.$に得られていることを仮定していましたが, 現実の世界ではなかなかそうもいきません.
- つまり一つの分布から発生しているわけでもなければ, 独立に得られているわけでもない.
- 例えばよくあるヤバい例は「時系列データ」です. これのモデリングは理論的には「確率過程」というものになるので軽い気持ちで触れるとヤケドします.
- 他に変数がないことを仮定しています. つまりカラムで得られているデータが全世界だと思っています.
などなど.
気をつけることは数多くあれど, 「もしこのように単純だとすると」というのは本質に迫っている可能性があります. 例えば関数をテイラー展開してその二次の項まで拾ってくるなどという営みはまさしくそうです. 本当の関数というのは無限に複雑であれど, 「大体こんぐらいでしょ」と近似する行為は一番大事なところを抜き出してきている可能性が高いわけです. もしもその本質っぽいものの抜き出しがうまくいっていないときは, 数理モデリング上だと前提がうまく満たされていない( テイラー展開の例であれば「収束半径から出てしまっている」など )と考えればよろしい, となります.
数理モデリングの意味というのはまさしくここにあるんじゃないかなと密かに思っています.
ものごとをある観点から捉えるときに, 定量的に, 論理的に, 何が成り立っていれば何をしていいか, ということを導くための武器を僕は数理的なモデリング以外に知りません.
後日談
"あなた"はこうしてデータから関係性のモデリングをすることができるようになり, 「なんか機械学習ってやつを使って面白いことやって」といっていた人もこのグラフを見て「ふんふん」とそれなりに面白そうな顔で話を聞いているそうな. めでたしめでたし.
参考文献
[1] 舟木直久, "確率論", 朝倉書店, 2004.
[2] 渡辺有祐, "グラフィカルモデル", 講談社, 2016.
[3] 鈴木譲, "ベイジアンネットワーク入門", 培風館, 2009.
[4] C.M. ビショップ, "パターン認識と機械学習(上)", 丸善出版, 2007.
[5] 井手剛, "異常検知と変化検知", 講談社, 2015.
[6] 吉田朋広, "数理統計学", 朝倉書店, 2006.
[7] J. Friedman and R. Tibshirani, “Sparse inverse covariance estimation with the graphical lasso,” Biostatistics, pp. 432–441, 2008.