ABC204 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC204(AtCoder Beginner Contest 204)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

A - Rock-paper-scissors

x,yがそれぞれ0,1,2の3パターンあるので全てのパターン数は3×3で9パターンです。
それぞれのパターンについてif文で場合分けし、答えを出力します。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
x,y=map(int, input().split())

# x,yの値で場合分け
if x==0 and y==0:
    print(0)
elif x==0 and y==1:
    print(2)
elif x==0 and y==2:
    print(1)    
elif x==1 and y==0:
    print(2)
elif x==1 and y==1:
    print(1)
elif x==1 and y==2:
    print(0)    
elif x==2 and y==0:
    print(1)
elif x==2 and y==1:
    print(0)
elif x==2 and y==2:
    print(2)

B - Nuts

問題文の条件通りにコードを書けばよいです。
すなわち
10<A[i]ならば(A[i]-10)個を収穫=答えにプラス
とすればよいです。

【提出】

# 入力の受け取り
N=int(input())
A=list(map(int, input().split()))

# 答えの格納用変数
ans=0

# i=0~N-1まで
for i in range(N):
    # A[i]が10より大きければ
    if 10<A[i]:
        # A[i]-10をansにプラスする
        ans+=A[i]-10

# 答えの出力
print(ans)

C - Tour

BFS(幅優先探索)を使います。
本問についてではないですが、BFSのやり方については動画で詳しく解説しています。ぜひ御覧ください。

都市1,都市2,...都市Nをスタート地点とした時、到達可能な都市の数をそれぞれ数えればよいです。
到達可能な都市を数えるためにBFSを使います。

BFSはグラフを探索する場合に使用するアルゴリズムです。
本問の場合、スタート都市を引数として指定→そこから到達可能な都市の数を返す関数をつくれば楽です。

BFSの具体的な手順は以下です。
(1)各道路の情報を受け取る
(2)スタート都市から到達可能な都市の数を数える変数(count)を用意する(初期値は1、スタート都市→スタート都市へ行けるため)
(3)訪問済みかどうかを確認するリスト(visited)を用意する(スタート都市は最初に訪問済としておく)
(4)キューを用意する
(5)キューにスタート都市を入れる。
(6)キューの左端から都市を取り出す(今いる都市：now_city)
(7)now_cityから行ける都市(行ける都市：to_city)を確認する
(8)to_cityが未訪問ならば
　・スタート都市から到達可能なのでcountにプラス1
　・to_cityを訪問済とする
(9)(6)～(8)をキューが空になるまで繰り返す
(10)到達可能な都市の数(count)を返す

関数ができたらスタート都市を1,2,3,...として順に関数へつっこみ、到達可能な都市を数えればよいです。

【提出】

# 入力の受け取り
N,M=map(int, input().split())

# 道路の情報を格納するリスト
connect=[[] for i in range(N+1)]

# M回受け取り
for i in range(M):
    # 入力の受け取り
    A,B=map(int, input().split())
    # connect[A]にBを追加
    # 都市1から都市2,3,4にいけるならconnect[1]=2,3,4
    connect[A].append(B)

# dequeをインポート
from collections import deque

# BFSの関数を用意
# スタート都市を引数→そこから行ける都市の数を返す
def BFS(start_city):
    # 行ける都市を数える変数
    # スタート都市→スタート都市には必ず行けるから1
    count=1
    # 訪問済み都市のリスト
    # 訪問済みならTrue、未訪問ならFalse
    visited=[False]*(N+1)
    # スタート都市は訪問済みにする
    visited[start_city]=True
    # キューを用意
    que=deque()
    # キューへスタート都市を追加
    que.append(start_city)
    # キューが空になるまで
    while 0<len(que):
        # 今いる都市
        now_city=que.popleft()
        # 今いる都市から行ける都市を順にto_cityへ
        for to_city in connect[now_city]:
            # もしto_cityが未訪問なら
            if visited[to_city]==False:
                # countにプラス1
                count+=1
                # to_cityを訪問済みにする
                visited[to_city]=True
                # キューへto_cityを追加
                que.append(to_city)
    # 行ける都市の数を返す
    return count

# 答えを格納する変数
ans=0

# x=1~N
for x in range(1,N+1):
    # xをスタート地点としたときに行ける都市の数を順に計算
    ans+=BFS(x)

# 答えの出力
print(ans)

D - Cooking

DPを使います。

2つのオーブンをそれぞれオーブンA、オーブンBと呼びます。
オーブンAでいくつかの料理をつくれば残りの料理は全てオーブンBで作らなければなりません。
よってこの問題を言い換えると以下のようになります。
Tの要素を2グループに分けてそれぞれ合計を計算、大きい方をSする。Sの最小値はいくらか。

例として以下の入力を考えます。
N：4
T：1 4 3 2
料理1,料理2,料理3をオーブンAで作ると1+4+3＝8分かかります。
料理4はオーブンBで作ります。Tの合計は10ですから、オーブンBを使う時間は(Tの合計)-(オーブンAを使う時間)=10-(1+4+3)=2だという事がわかります。
すべての料理を作るのにかかる時間(=S)は8と2の大きい方、すなわち8です。

例からわかるように(オーブンAを使う時間)と(Tの合計-オーブンAを使う時間)の大きい方がすべての料理を作るのにかかる時間です。
(Aのオーブンを使う時間)はTからいくつかの要素を組み合わせて合計した数です。
ということはTからいくつかの要素を組み合わせて合計したとき、作れる数はなにかがわかれば解けます。
(Tからいくつかの要素を組み合わせて合計した時0,1,2,...は作れるか？を考えます)
このように数列の要素をいくつか組み合わせて合計したときに作れる数を探索する問題は 「部分和問題」 と言います。

「部分和問題」はDPで解くことができます。
DPとは「ある状態までの答えがわかっていれば→その次の状態の答えも出せる」という手続きを何度も行って最終的な答えを出す方法です。

具体的な手順は以下です。
(1)表を作る
(2)すぐにわかるところを埋める
(3)表の小さい方から答えにたどり着くまで埋める
(4)答えを出力する

(1)表を作る
『i番目までの数を組み合わせてxを作れるか』を確認する表を作ります。
実装では二次元配列を作ります。名前はdpとします。
行がi、列がxを表します。
T[0]は0番目の数を表します。が、0番目の数なんて存在しません。便宜上0を入れておきます。

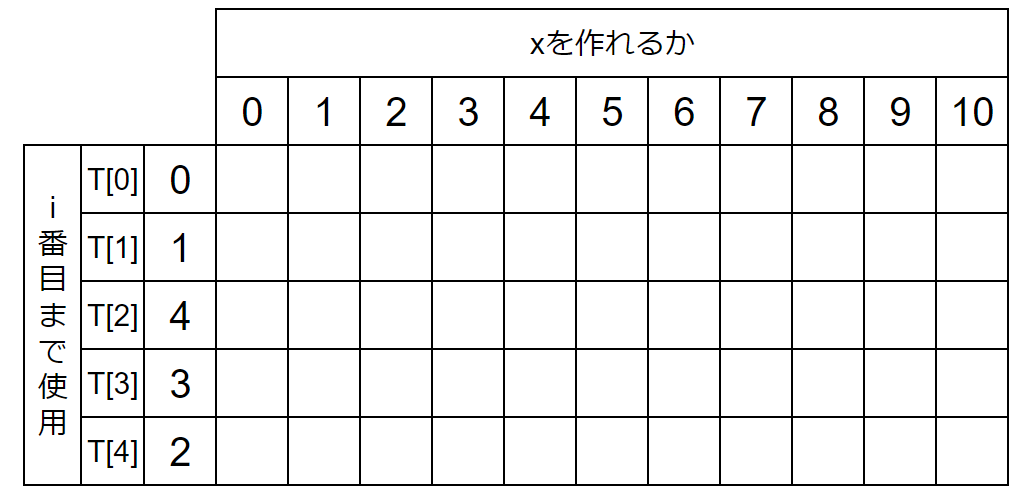
(2)すぐにわかるところを埋める
すぐに埋まるところは0行目です。

まずdp[0][0]を考えます。dp[0][0]は『0番目までの数を組み合わせて0を作れるか』という意味です。
0番目の数は「0」で、「0」を使えば0は作れますから、ここは○です。

dp[0][1]はどうでしょうか。dp[0][1]は『0番目までの数を組み合わせて1を作れるか』という意味です。
0番目の数は「0」で、「0」だけでは1は作れません。ここは×(バツ)です。
同様の理由でdp[0][2],dp[0][3],...も×(バツ)です。

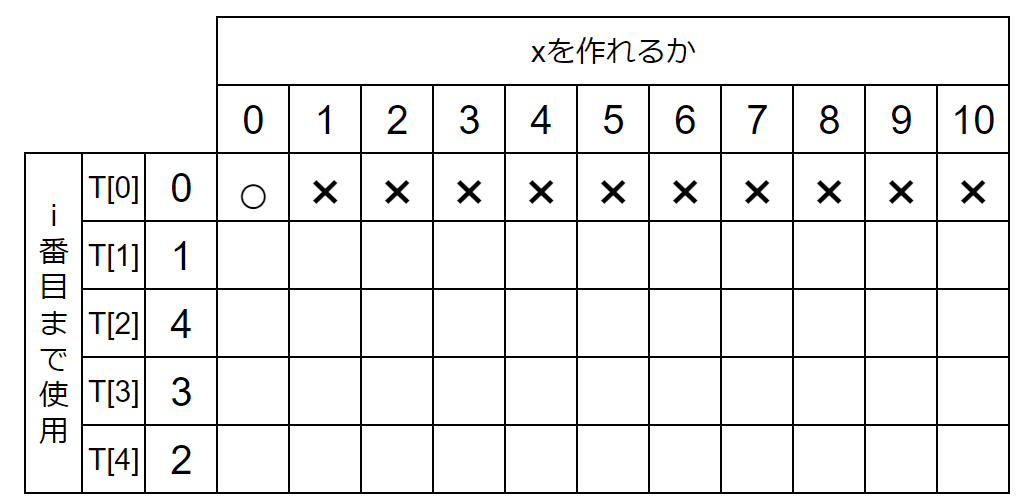
(3)表の小さい方から答えにたどり着くまで埋める
まず1行目を考えましょう。

dp[1][0]は『1番目までの数を組み合わせて0を作れるか』という意味です。
注意が必要なのは「1番目の数を組み合わせて」ではなく「1番目までの数を組み合わせて」というところです。
1番目の数は「1」ですが、必ずしも組み合わせに使う必要はありません。
1番目までの数ということは0～1番目の数、すなわち「0」と「1」が使えるという意味です。
0だけを使えば「0」は作れますから、dp[1][0]は○です。

dp[1][1]も○です。dp[1][1]は『1番目までの数を組み合わせて1を作れるか』という意味です。
1番目の数である「1」を使えば1を作れます。
1行目は以下のようになります。

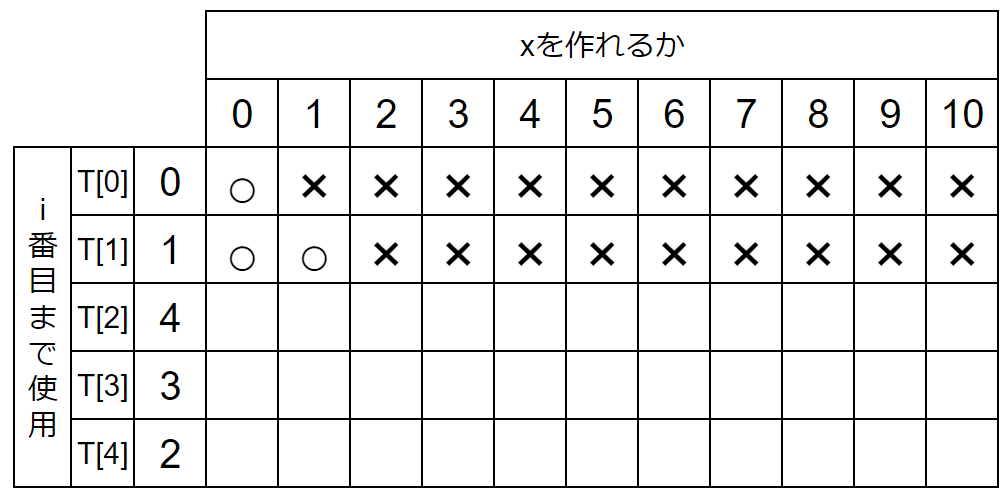
次に2行目を考えましょう。

dp[2][0]は『2番目までの数を組み合わせて0を作れるか』です。
dp[1][0]が○、すなわち『1番目までの数を組み合わせて0を作れるか』が○だったわけですから、当然作れます。
dp[2][0]は○です。

dp[2][1]は『2番目までの数を組み合わせて1を作れるか』です。
dp[1][1]が○、すなわち『1番目までの数を組み合わせて1を作れるか』が○だったわけですから、こちらも当然作れます。
dp[2][1]も○です。

よくよく考えると『(i-1)番目までの数を組み合わせてxを作れるか』が○であれば、『i番目までの数を組み合わせてxを作れるか』も当然○になることがわかります。
((i-1)番目までの数を組み合わせてxを作った方法がそのまま使えるため。「i番目の数を組み合わせて」ではなく「i番目までの数を組み合わせて」であることに注意してください)

一般に考えると以下のようになります。
dp[i-1][x]が○→dp[i][x]も○

dp[2][3]は×(バツ)です。
(2番目までの数=0,1,4の組み合わせでは3を作れません)

dp[2][4]はどうでしょうか。
注目すべきはdp[1][0](『1番目までの数を組み合わせて0を作れるか』)が○であることです。
で、あれば2番目の数「4」を「1番目までの数で0を作った組み合わせ」に追加すれば4ができます。
ゆえにdp[2][4]は○です。
具体的に何をしているか説明しますと、
1番目までの数=0,1で0は作れます。(0番目の数「0」を使う)
2番目の数「4」を組み合わせに追加すれば4が作れます。(0番目の数「0」と2番目の数「4」を組み合わせる)

もうひとつ例をあげましょう。いま途中まで表が埋まっており、次に黄色の箇所(dp[3][7])が○か×(バツ)か考えています。

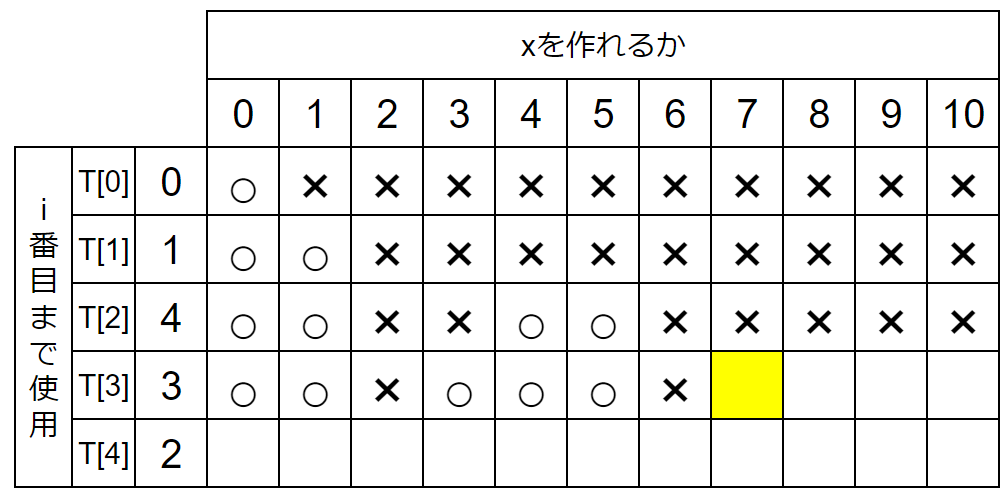
dp[3][7]は『3番目までの数を組み合わせて7を作れるか』です。
3番目の数は「3」です。
dp[2][4](『2番目までの数を組み合わせて4を作れるか』)は○です。
2番目までの数を組み合わせて4を作った組み合わせに3番目の数「3」を追加すれば7が作れます。
ゆえにdp[3][7]は○です。

一般に考えると以下のようになります。
dp[i-1][x-T[i]]が○→dp[i][x]も○
ただしx-T[i]がマイナスになると表をはみ出すので、0<=x-T[i]という条件が付きます。

まとめましょう。
・dp[i-1][x]が○→dp[i][x]も○
・dp[i-1][x-T[i]]が○→dp[i][x]も○(0<=x-T[i])
実装ではi=1~N、x=0～(Tの合計)と二重ループを回すことで表を全て埋めることができます。

(4)答えを出力する
表をすべて埋めると以下のようになります。

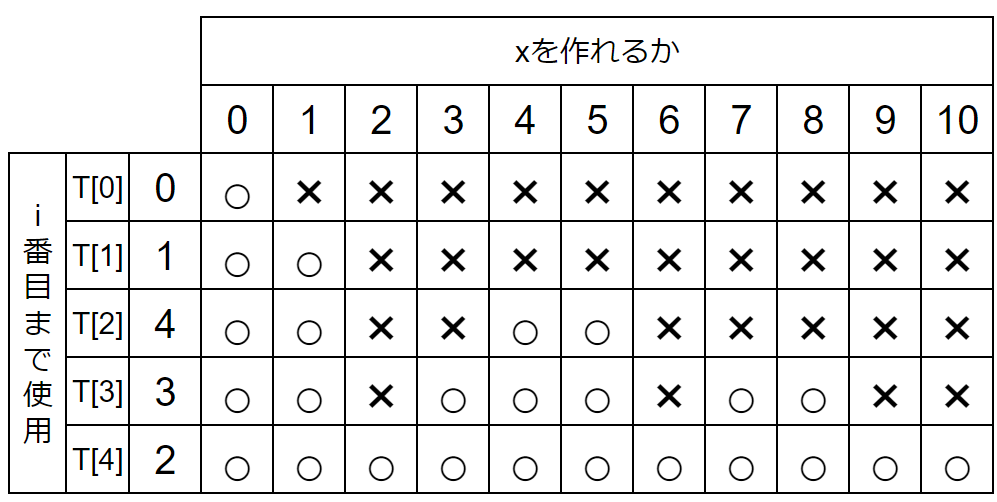
最後の行は『N(=4)番目までの数を組み合わせてxを作れるか』を表します。
「N番目の数まで」=「Tの要素全て」です。つまりTの要素をいくつか組み合わせて合計したとき、作れうる数が表からわかります。

あとはN行目が○のxそれぞれについて、xと(Tの合計-x)を計算していきます。これらの大きい方が料理をすべて作るのにかかる時間です。
そのうち一番小さいものを出力すればOKです。

pythonだとTLEするのでpypyで提出します。

【提出】

# pypyで提出

# 入力の受け取り
N=int(input())
# Tは先頭に[0]を追加して受け取り
T=[0]+list(map(int, input().split()))

# Tの合計
T_sum=sum(T)

# 表を作る
# 『i番目までの数を組み合わせてxを作れるか』
# 例：『0番目の数(=0)を組み合わせて「0」を作れる』→dp[0][0]==True
dp=[[False]*(T_sum+1) for i in range(N+1)]
dp[0][0]=True

# i=1~N i番目までの数を組み合わせる
for i in range(1,N+1):
    # x=0~T_sum xを作れるか確認
    for x in range(T_sum+1):
        # もし『(i-1)番目までの数を組み合わせてxを作れる』(→dp[i-1][x]=True)ならば
        if dp[i-1][x]==True:
            # 『i番目までの数を組み合わせてxを作れる』(→dp[i][x]=True)
            dp[i][x]=True
        # もし0<=x-T[i] かつ　『(i-1)番目までの数を組み合わせてx-T[i]を作れる』ならば
        if 0<=x-T[i] and dp[i-1][x-T[i]]==True:
            # 『i番目までの数を組み合わせてxを作れる』(→dp[i][x]=True)            
            dp[i][x]=True

# 答えを格納する変数(初期値はバカでかい数)
ans=10**20

# x=0~T_sum
for x in range(T_sum+1):
    # 『N番目までの数を組み合わせてxを作れる』ならば
    if dp[N][x]==True:
        # max(x,T_sum-x)が料理をすべて作るのにかかる時間=答えの候補
        # それまでのansより小さければ更新
        ans=min(ans,max(x,T_sum-x))

# 答えの出力
print(ans)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】