ABC233(AtCoder Beginner Contest 233) A~E問題の解説記事です。
灰色~茶色コーダーの方向けに解説しています。
その他のABC解説、動画などは以下です。
A - 10yen Stamp
(Y-X)を10で割って切り上げを計算すればよいです。
ただしY≤Xの場合は10円切手を貼る必要がないので「0」となります。
切り上げの実装は
・(Y-X)が10で割り切れる → (Y-X)//10
・(Y-X)が10で割り切れない → (Y-X)//10+1
とするのがわかりやすいです。
入力の受け取り、出力がわからない方は以下の記事を参考にしてください。
【提出】
# 入力の受け取り
X,Y=map(int,input().split())
# X<Yならば
if X<Y:
# (Y-X)が10で割り切れる⇔(Y-X)÷10の余りが0 ならば
if (Y-X)%10==0:
# (Y-X)//10を出力
print((Y-X)//10)
# そうでないならば((Y-X)が10で割り切れない)
else:
# (Y-X)//10+1を出力
print((Y-X)//10+1)
# そうでないならば(Y≤X)
else:
# 0を出力
print(0)
B - A Reverse
Sをリストに展開し、
左:1~(L-1)文字目
中央:L~R文字目
右:(R+1)文字目~末尾
の3つに分け、中央だけを反転して結合します。
pythoでは文字やリストが0インデックス、すなわち1文字目=S[0]、2文字目=S[1]、...となることに注意してください。
すなわち実装では以下のようになります。
左:0~(L-2)文字目
中央:(L-1)~(R-1)文字目
右:R文字目~末尾
反転は
文字列[::-1]
リストの結合は
"".join(リスト)
と書きます。どちらもググればすぐ出てくるので頑張って覚える必要はありません。
【提出】
# 入力の受け取り
L,R=map(int,input().split())
S=input()
# Sを一文字ずつリストへ展開
S_list=list(S)
# Sの0~(L-2)文字目
S_left=S_list[:L-1]
# Sの(L-1)~(R-1)文字目
S_center=S_list[L-1:R]
# SのR文字目~末尾
S_right=S_list[R:]
# 中央を反転
S_center=S_center[::-1]
# リストを結合
S=S_left+S_center+S_right
# 文字列へ結合
S_join="".join(S)
# 答えの出力
print(S_join)
C - Product
制約を見てみるとΠLi≤10^5となっています。これはそれぞれの袋から1つずつボールを取り出すパターン数が10^5以下であるということです。
よって全ての組み合わせを計算しても間に合います。
全ての組み合わせについての計算を実装するには以下のように行います。
(1)計算結果を格納するリスト(pro)を用意。初期値は1とする。
i番目の袋について計算する。
(2)結果一時保存用のリスト(tmp_pro)を用意。
(3)i番目の袋のボール全てについて、proの中身全てと掛け算してtmp_proへ格納
(4)proをtmp_proで更新
(5)(2)~(4)をN番目の袋まで繰り返す
これでproに全てのパターンについての計算結果が格納されます。
後はXと一致するものがいくつあるか確認します。
公式解説の通りDFSを使っても解けます。【提出2】にサンプルコードを書いています。
ただし、再帰関数を使うので少々ややこしいです。
本問についてではないですが、DFSについて動画で解説を作っているのでそちらも是非ご覧ください。
【提出1】
# 入力の受け取り
N,X=list(map(int,input().split()))
# L,aの格納リスト
L=[]
a=[]
# N回
for i in range(N):
# 一旦リストで受け取り
tmp=list(map(int,input().split()))
# リストの0番目=L
L.append(tmp[0])
# リストの1番目~=a
a.append(tmp[1:])
# 全ての掛け算パターンの結果
pro=[1]
# i=0~(N-1)
for i in range(N):
# 一時的に結果を格納するリスト
tmp_pro=[]
# i番目の袋のa全てについて
for ai in a[i]:
# ここまでの全ての掛け算パターンの結果
for p in pro:
# 掛け算して格納
tmp_pro.append(ai*p)
# proをtmp_proで更新
pro=tmp_pro
# 結果がXとなったパターンを数える
ans=pro.count(X)
# 答えを出力
print(ans)
【提出2】
# 再帰回数上限を10^6回へ
import sys
sys.setrecursionlimit(10**6)
# 入力の受け取り
N,X=map(int,input().split())
L=[]
a=[]
# N回
for i in range(N):
# 入力の受け取り
tmp=list(map(int,input().split()))
L.append(tmp[0])
a.append(tmp[1:])
# 答え
ans=0
# 掛け算を行っていく関数
# 引数:積(pro),袋の番号(i)
def DFS(pro,i):
# ansを更新できるように
global ans
# 最後の袋まで掛け算したら
if i==N:
# 積=Xなら
if pro==X:
# 答えにカウント
ans+=1
# 関数を終了
return
# j=0~(L[i]-1)
for j in range(L[i]):
# 掛け算して次の袋へ
DFS(pro*a[i][j],i+1)
# 積=1,袋の番号0からスタート
DFS(1,0)
# 答えを出力
print(ans)
D - Count Interval
(l,r)の全組について、普通に区間和を計算していくとO(N^3)となり、間に合いません。
まず区間(l,r)の計算を高速で行う方法を考えます。これには累積和(Cumulative sum)を使います。
例として以下を考えましょう。
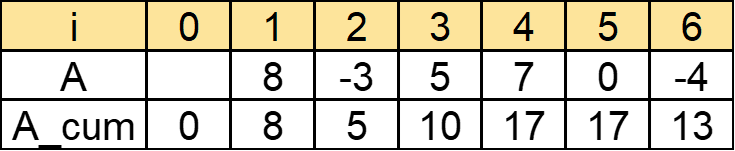
A:8 -3 5 7 0 -4
Aの累積和をA_cum[i]=(Aの0~iまでの和)とします。
計算は以下のようにすることでO(N)でできます。
・(i=0) A_cum[0]=0
・(1≤i) A_cum[i+1]=A_cum[i]+A[i]
区間(l,r)の和はA_cum[r]-A_cum[l-1]と計算できます。
例えばA[2]~A[5]の和は
A_cum[5]-A_cum[2-1]
=A_cum[5]-A_cum[1]
=17-8
=9
となります。
なぜ累積和で区間和が計算できるのか説明します。
例えば上記例なら
A_cum[5]-A_cum[2-1]
=(Aの0~5までの和)-(Aの0~1までの和)
=(0+8+(-3)+5+7+0)-(0+8)
=(-3)+5+7+0
といい感じにいらない部分を消せるからです。
累積和を事前に計算しておけば区間和はO(1)で計算できます。
しかし(l,r)全ての組を計算するとO(N^2)となり、やはりTLEします。
累積和を使うなら以下が成り立てばよいということがわかります。
A_cum[r]-A_cum[l-1]=X
変形します。
A_cum[l-1]=A_cum[r]-X
よって
1≤l≤r かつ A_cum[l-1]=A_cum[r]-X
となるようなものがいくつあるか計算していきます。
具体的にはiを1から一つずつ増やしながら
・「A_cum[i-1]」をカウント
・「A_cum[i]-K」の個数を答えとしてカウント
を繰り返していきます。
「A_cum[i-1]」と「A_cum[i]-K」の個数のカウントには連想配列(defaultdict)を使います。
使ったことがない人は以下を参照してください。
defaultdict(連想配列)について
辞書または連想配列と言います。
キー:値
というような対応付を行えるデータ構造です。
連想配列はdict()と書くことでも使えますが、デフォルトの値(初期値)が設定できません。そのため存在チェックなど色々面倒が発生します。
その面倒を避けるためにdefaultdictを使います。
import:from collections import defaultdict
作成(デフォルト0):変数名=defaultdict(int)
キー、値の登録:変数名[キー]=値
値の取り出し:変数名[キー]
【使用例】
# インポート
from collections import defaultdict
# 作成(デフォルト0):変数名=defaultdict(int)
dictionary=defaultdict(int)
# キー、値の登録:変数名[キー]=値
dictionary[5]=1
# 値の取り出し:変数名[キー]
x=dictionary[5]
詳しく知りたい人は以下を参照してください。
【提出】
# 入力の受け取り
N,K=map(int,input().split())
A=list(map(int,input().split()))
# Aの累積和
A_cum=[0]*(N+1)
# i=0~(N-1)まで
for i in range(N):
# 累積和を計算
A_cum[i+1]=A_cum[i]+A[i]
# defaultdictをインポート
from collections import defaultdict
# 連想配列
X=defaultdict(int)
# 答えをカウント
ans=0
# i=1~Nまで
for i in range(1,N+1):
# A_cum[i-1]が増える
X[A_cum[i-1]]+=1
# A_cum[i]-Kとなるものをカウント
ans+=X[A_cum[i]-K]
# 答えを出力
print(ans)
E - Σ[k=0..10^100]floor(X/10^k)
筆算のイメージで考えます。
例としてX=12345で考えます。
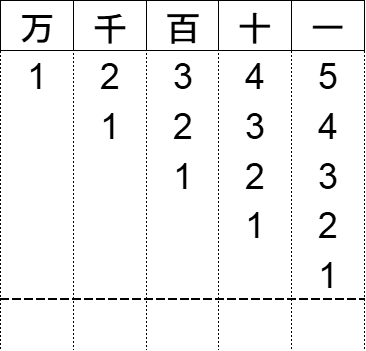
行う足し算は以下のようになります。
まず繰り上がりは気にせずに全ての桁をそのまま足し算しましょう。
万の位:1
千の位:1+2
百の位:1+2+3
...
となっているので、
「千の位の和」=「万の位の和」+「千の位の数」
「百の位の和」=「千の位の和」+「百の位の数」
...
というように計算していけば計算量は各桁O(1)で済みます。
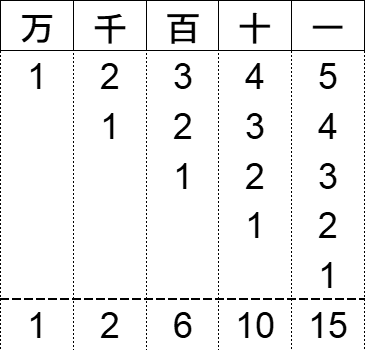
小さい位から繰り上げを考慮しつつ数字を確定させていきます。
「一の位」=15ですので、繰り上がりは10で割った商=1です。繰り上がりは「十の位」に足します。
「一の位」は「15」の一番右端すなわち「5」で確定します。
「十の位」は「一の位」から繰り上がりを1もらっているので10+1=11になっています。
「一の位」同様に繰り上がりは10で割った商=1となり、これを「百の位」へ足します。
「十の位」は「11」の一番右端すなわち「1」で確定します。
この処理を一番大きい位まで繰り返せば答えが出せます。
実装ではXを文字列として受け取り、整数⇔文字列へ変換しながら上記の処理を行っていきます。
【提出】
# 入力の受け取り
X=input()
N=len(X)
# Xを一文字ずつリストへ展開
X_list=list(X)
# i=0~(N-1)
for i in range(N):
# 整数へ変換
X_list[i]=int(X_list[i])
# 各桁ごとの計算結果
d=[0]*(N)
# 0桁目はX_list[0]
d[0]=X_list[0]
# i=1~N-1
for i in range(1,N):
# 各桁の値を計算
d[i]=d[i-1]+X_list[i]
# 桁の小さい順に確定させていく
# i=(N-1)~1
for i in range(N-1,0,-1):
# 繰り上がり=10で割った商
d[i-1]+=d[i]//10
# 文字列へ
d[i]=str(d[i])
# 1桁目が確定の値
d[i]=d[i][-1]
# 一番大きい桁を文字列へ
d[0]=str(d[0])
# 結合
ans="".join(d)
# 答えの出力
print(ans)
【広告】
『AtCoder 凡人が『緑』になるための精選50問詳細解説』
AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段:100円(Kindle Unlimited対象)
【kindle】
【booth(pdf)】
1~24問目まではサンプルとして無料公開しています
『AtCoder ABC201~225 ARC119~128 灰・茶・緑問題 超詳細解説』
ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif:0~1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。
サンプルを5問分公開しています
Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える?】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。
値段:300円(Kindle Unlimited対象)
【kindle】
【booth(pdf)】
ARC119~128の部分のみ抜粋した廉価版 もあります。
値段:200円(Kindle Unlimited対象)
【kindle】
【booth(pdf)】
『Excelでリバーシを作ろう!! マクロ、VBAを1から学ぶ』
Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です!
マクロ、VBAが全くわからない人でも大丈夫! 丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます!
値段:300円(Kindle Unlimited対象)
サンプルとして「準備」~「三目並べ」を無料公開しています。
【kindle】
【booth(pdf】